Foucault-Pendel

Bildquelle: https://commons.wikimedia.org/wiki/File:Foucault_portre_crop.jpg

Zátonyi Sándor, (ifj.) Fizped, CC BY 3.0 <https://creativecommons.org/licenses/by/3.0>, via Wikimedia Commons

Das Foucault-Pendel ist nach dem französischen Physiker Léon Foucault (1819 – 1868) benannt. Am 3. Januar 1851 führte er im Keller seines Hauses einen Versuch durch, bei dem er ein zwei Meter langes Pendel dicht über dem Boden schwingen ließ und seine Bahn genau markierte. Er beobachtete, dass sich die Schwingungsebene des Pendels langsam drehte. Die Schwerkraft, die nur senkrecht wirkt, konnte diese Drehung nicht verursachen, und keine weitere äußere Kraft wirkte auf das Pendel ein. Also war es nicht das Pendel, sondern der Boden/die Erde, der/die seine Ausrichtung änderte. Genau genommen beschreibt das Pendel gegenüber dem Boden eine Rosettenbahn mit extrem schmalen Blättern, wodurch es als ein ebenes Pendel erscheint, dessen Schwingungsebene sich langsam dreht. Das Foucaultsche Pendel war also der erste echte Beweis für die Rotation der Erde.

Ich möchte in diesem Experiment ein Foucaultsches Pendel mit möglichst einfachen Mitteln nachstellen und damit die Erddrehung beweisen und zwar nicht nur rein qualitativ, sondern auch quantitativ. Befände sich das Pendel etwa auf dem Nordpol, so würde sich die Erde unter dem Pendel innerhalb eines Tages (genauer in 23 h 56 min) drehen. Die Schwingungsebene des Pendels hätte dort also eine Winkelgeschwindigkeit von ω_Erde = 2·π / 86160 rad/sek = 360 / 86160 grad/sek. Am Äquator wäre die Winkelgeschwindigkeit indes 0, da die Komponente der Erdwinkelgeschwindigkeit (diese zeigt ja in Richtung der Erdrotationsachse) senkrecht zum Boden am Äquator 0 ist! Für den Breitengrad φ gilt dann allgemein: ω_Pendel = ω_Erde · sin(φ).

Bei mir in Graz müsste sich also das Foucaultsche Pendel innerhalb von 10 Minuten um lediglich 1.836° weiterdrehen. Dies zu erfassen wird bestimmt nicht leicht.

Hier (https://www.youtube.com/watch?v=SoZVb5WaK9I) bin ich auf ein tolles Video gestoßen. Die darin gezeigte Vorgehensweise zur Bestimmung des Positionswinkels der Schwingungsebene möchte ich übernehmen. Ich verwende hierfür aber wie von mir gewohnt einfache Mitteln, konkret LEGO-Bauteile.

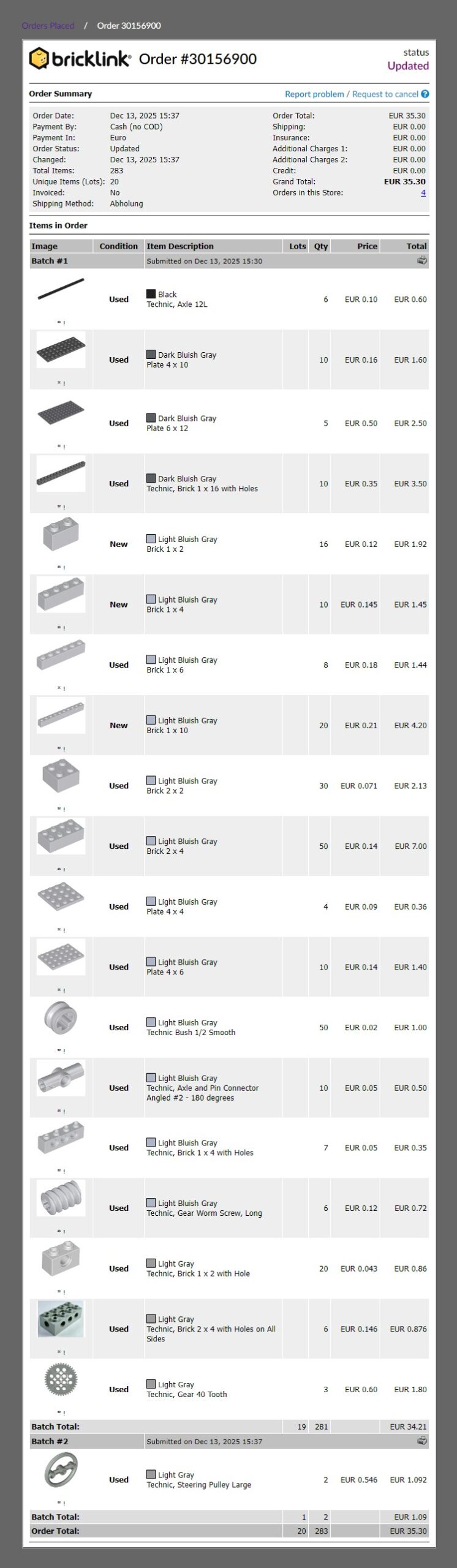
Meine Bricklink-Bestellung um insgesamt 35 Euro:

Der Schirm für den Laserstrich:

Hier wird der Linienlaser montiert:

Ich verwende zwei Schneckenrad-Zahnrad-Kombinationen. Die beiden Zahnräder besitzen 40 bzw. 24 Zähne. Daher beträgt die Untersetzung 1/40 · 1/24 = 1/960!

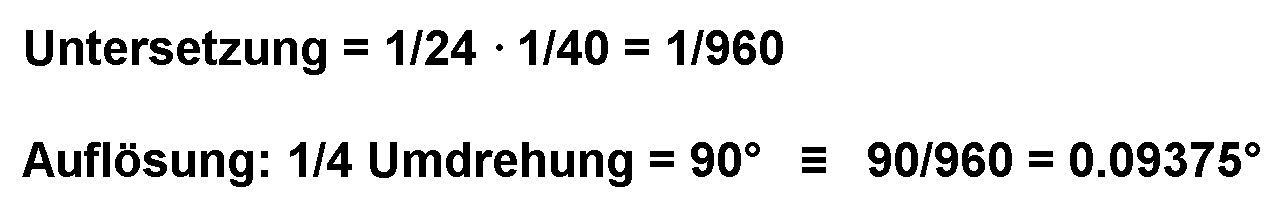
Ich werde mit dem Drehrad manuell ca. 1/4 Umdrehung = 90° auflösen können. Dies entspricht dann einer Drehung der ganzen Anordung um nur 0.09375°. Nach 10 Minuten sollte ich also ca. 1.836/0.09375 = ca. zwanzig 1/4-Drehungen = 5 volle Umdrehungen machen müssen…

Als Pendelkörper verwende ich ein Senklot. Dieses bekommt man zusammen mit dem Linienlaser um wenig Geld auf Amazon:

Erläuterung der Messmethode:

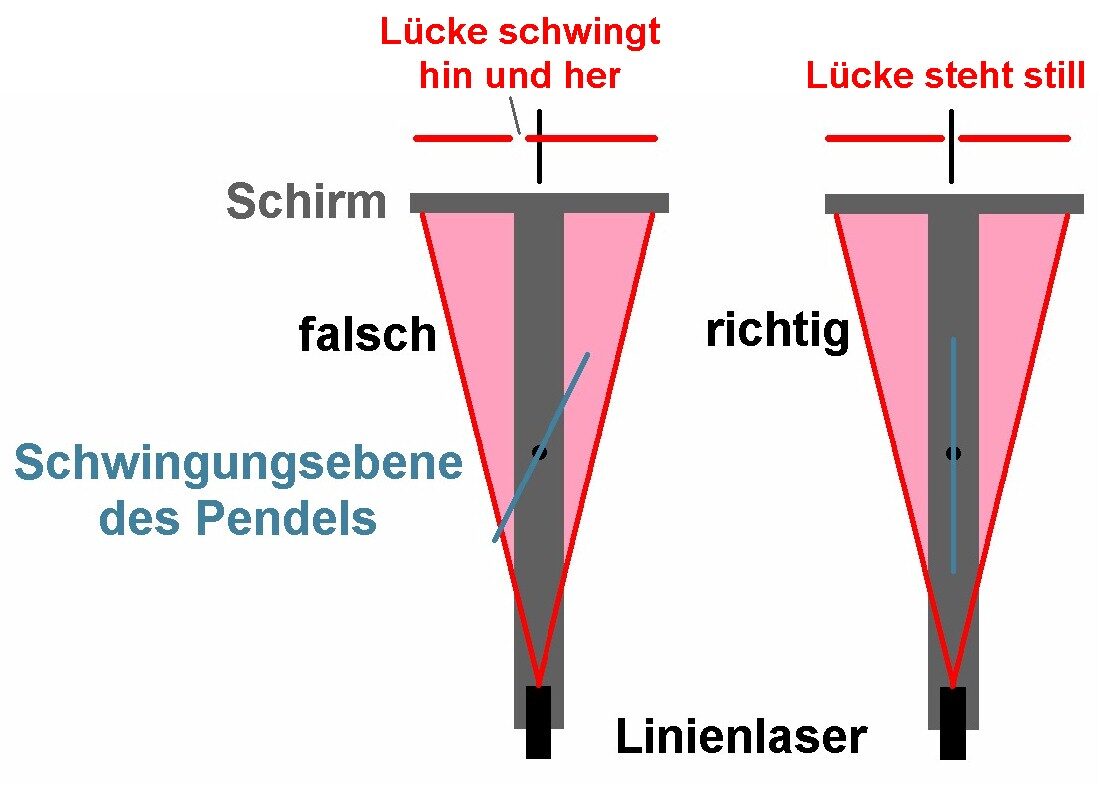
Ist die Ausrichtung der Laserapparatur noch falsch, wandert die Schattenlücke des Pendelseils am Schirm um den Kontrollstrich herum nach links und rechts. Stimmt die Ausrichtung, bleibt die Schattenlücke genau über dem Kontrollstrich stehen.

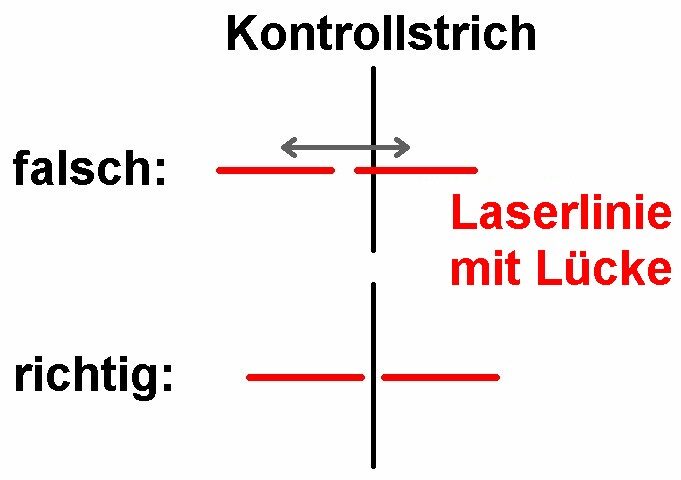
Ursprünglich hatte ich ja vor, das Legorad manuell immer um 90° zu drehen und die Anzahl der Drehungen mitzuzählen. Das geht aber einfacher bzw. automatisiert besser. Dazu benötigt man nur einen Arduino mit 16 x 2 Display, einen Schrittmotortreiber und einen Schrittmotor. Mit einem Taster dreht man den Schrittmotor immer um 90°. Die Anzahl n der Drehungen wird am Display angezeigt. Zudem sieht man am Bildschirm auch die Zeit t in Sekunden. Mit einem zweiten Taster setzt man n und t auf Null.

Vorgangsweise: Man stößt das Pendel an. Danach orientiert man den Legoarm durch Tastendruck und 90°-Schritte parallel zur Schwingungsebene. Nun betätigt man den zweiten Taster und stellt die Anzahl der 90°-Drehungen und die Zeit auf 0. Jetzt wartet man z.B. 5 Minuten und bringt dann den Legoarm durch Tastendruck wieder parallel zur Schwingungsebene. Ist dies geschehen, notiert man sich das angezeigte n und die Zeit t. Nach weiteren z.B. 5 Minuten wiederholt man dies. Auf diese Weise erhält man den zurückgelegten Winkel φ = n · 90° / 960 in Abhängigkeit von der Zeit t. Es sollte sich eine steigende Gerade ergeben mit dem Anstieg k = φ / t = n · 90° / (960 · t) = ω_Pendel. Nach Beendigung der Messung drückt man einen dritten Taster (im Schaltplan mit der Bezeichnung „return“ versehen), welcher den Schrittmotor umgekehrt antreibt. Damit fährt man den LEGO-Arm wieder in die Startposition und ist bereit für neue Messungen.

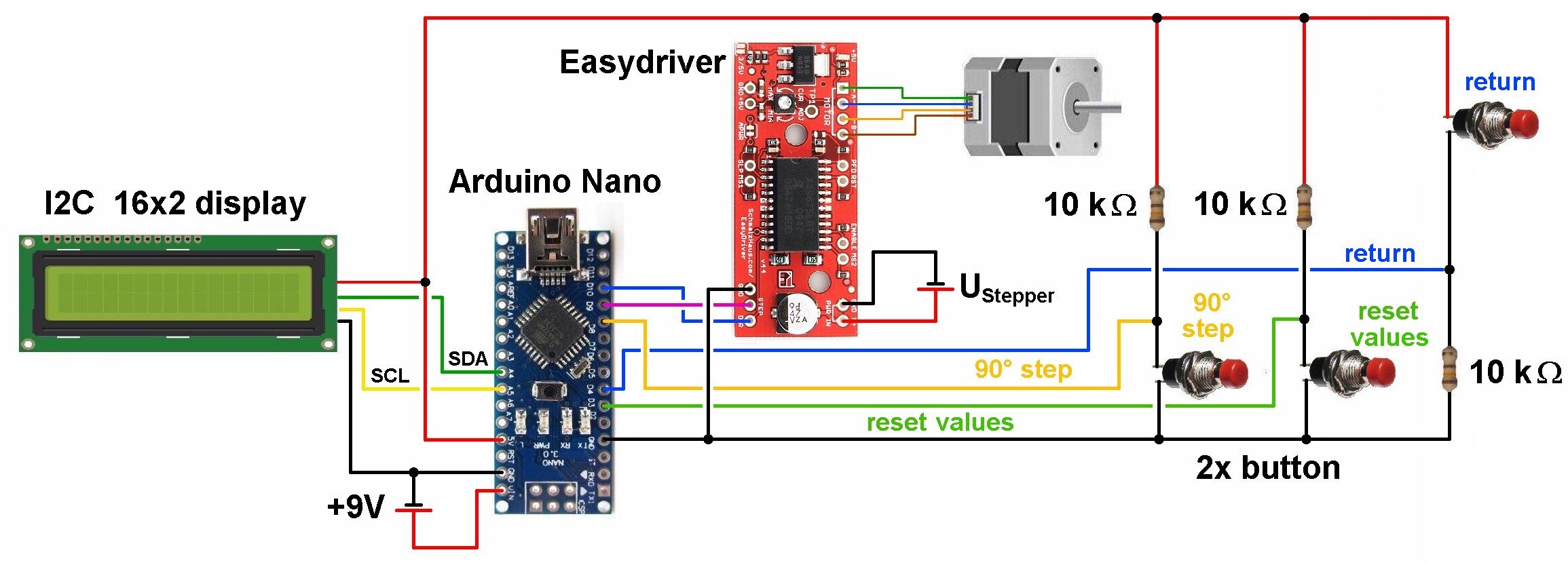
Der komplette Schaltplan:

Der einfache Arduino-Code:

#include <LiquidCrystal_I2C.h>
#include <Wire.h>

LiquidCrystal_I2C lcd(0x27,16,2);  // set the LCD address to 0x27 for a 16 chars and 2 line display. ACHTUNG: Adresse kann auch 0x3F sein !!!

// Anschlüsse:
// GND - GND
// VCC - 5V
// SDA - ANALOG Pin 4
// SCL - ANALOG pin 5

#include <AH_EasyDriver.h>

//AH_EasyDriver(int RES, int DIR, int STEP);
// RES -> RESOLUTION per full revolve
// DIR -> DIRECTION PIN
// STEP -> STEPPING PIN

AH_EasyDriver stepper(200,10,9);   // Initialisation

// DIR-Pin = Pin 10
// STEP-Pin = Pin 9

const int buttonPin_reset = 3;       // the number of the pushbutton pin for resetting the values
const int buttonPin_return = 4;     // the number of the pushbutton pin for return of the arm
const int buttonPin_step = 8;     // the number of the pushbutton pin for a 90 degree step

int n;
long millis_start;


// ===========================
// =======   SETUP   =========
// ===========================

void setup()
   {
    Serial.begin(9600);
    
    lcd.begin();        // initialize the lcd
    lcd.backlight();
    lcd.setCursor(0,0);
    lcd.print("Foucaultpendel");
    lcd.setCursor(0,1);
    lcd.print("Version 1.0");
    
    delay(3000);
    
    lcd.setCursor(0,0);
    lcd.print("               ");
    lcd.setCursor(0,1);
    lcd.print("             ");


    stepper.setSpeedRPM(20);          // RPM , rotations per minute

    // RPM = 1 entspricht einer Umlaufszeit von 30 Sekunden!!!
    // RPM = 10 entspricht einer Umlaufszeit von 3 Sekunden!!!
    // RPM = 20 entspricht einer Umlaufszeit von 1.5 Sekunden!!!
    // =======================================================

    //stepper.setMicrostepping(3);            // 0 -> Full Step                                
                                          // 1 -> 1/2 microstepping
                                          // 2 -> 1/4 microstepping
                                          // 3 -> 1/8 microstepping

    n = 0;
    millis_start = 0;
        
   }


// ===========================
// =======    LOOP   =========
// ===========================

void loop()
   {
    while(digitalRead(buttonPin_step))
       {
        lcd.setCursor(0,0);
        lcd.print("n = ");
        lcd.print(n);
        lcd.print("     ");

        lcd.setCursor(0,1);
        lcd.print("t = ");
        lcd.print((millis() - millis_start) / 1000);
        lcd.print(" sek       ");
        
        if(digitalRead(buttonPin_reset) == 0)    // reset of the n and t values
           {
            n = 0;
            millis_start = millis();
           }

        while(digitalRead(buttonPin_return))    // return of the LEGO arm
           {
            stepper.move(10,0);    // 0 = im Uhrzeigersinn, 1 = gegen Uhrzeigersinn
           }
     
       }

    n = n + 1;

    stepper.move(400,1);    // 90 degree step, 0 = im Uhrzeigersinn, 1 = gegen Uhrzeigersinn
    
   }

100

101

102

103

104

105

106

107

108

#include <LiquidCrystal_I2C.h>

#include <Wire.h>

LiquidCrystal_I2C lcd(0x27,16,2); // set the LCD address to 0x27 for a 16 chars and 2 line display. ACHTUNG: Adresse kann auch 0x3F sein !!!

// Anschlüsse:

// GND - GND

// VCC - 5V

// SDA - ANALOG Pin 4

// SCL - ANALOG pin 5

#include <AH_EasyDriver.h>

//AH_EasyDriver(int RES, int DIR, int STEP);

// RES -> RESOLUTION per full revolve

// DIR -> DIRECTION PIN

// STEP -> STEPPING PIN

AH_EasyDriver stepper(200,10,9); // Initialisation

// DIR-Pin = Pin 10

// STEP-Pin = Pin 9

const int buttonPin_reset = 3; // the number of the pushbutton pin for resetting the values

const int buttonPin_return = 4; // the number of the pushbutton pin for return of the arm

const int buttonPin_step = 8; // the number of the pushbutton pin for a 90 degree step

int n;

long millis_start;

// ===========================

// ======= SETUP =========

// ===========================

void setup()

{

Serial.begin(9600);

lcd.begin(); // initialize the lcd

lcd.backlight();

lcd.setCursor(0,0);

lcd.print("Foucaultpendel");

lcd.setCursor(0,1);

lcd.print("Version 1.0");

delay(3000);

lcd.setCursor(0,0);

lcd.print(" ");

lcd.setCursor(0,1);

lcd.print(" ");

stepper.setSpeedRPM(20); // RPM , rotations per minute

// RPM = 1 entspricht einer Umlaufszeit von 30 Sekunden!!!

// RPM = 10 entspricht einer Umlaufszeit von 3 Sekunden!!!

// RPM = 20 entspricht einer Umlaufszeit von 1.5 Sekunden!!!

// =======================================================

//stepper.setMicrostepping(3); // 0 -> Full Step

// 1 -> 1/2 microstepping

// 2 -> 1/4 microstepping

// 3 -> 1/8 microstepping

n = 0;

millis_start = 0;

}

// ===========================

// ======= LOOP =========

// ===========================

void loop()

{

while(digitalRead(buttonPin_step))

{

lcd.setCursor(0,0);

lcd.print("n = ");

lcd.print(n);

lcd.print(" ");

lcd.setCursor(0,1);

lcd.print("t = ");

lcd.print((millis() - millis_start) / 1000);

lcd.print(" sek ");

if(digitalRead(buttonPin_reset) == 0) // reset of the n and t values

{

n = 0;

millis_start = millis();

}

while(digitalRead(buttonPin_return)) // return of the LEGO arm

{

stepper.move(10,0); // 0 = im Uhrzeigersinn, 1 = gegen Uhrzeigersinn

}

n = n + 1;

stepper.move(400,1); // 90 degree step, 0 = im Uhrzeigersinn, 1 = gegen Uhrzeigersinn

}

Die LEGO-Achse verklebte ich mit einer biegsamen Schrittmotorkupplung:

Der bis auf das Pendel selbst fertige Aufbau:

Das Senklot ist inzwischen eingetrudelt:

Aufhängung 1: Nagel

Leider verhält sich das Pendel nicht so wie erhofft. Erhofft wurde nämlich, dass das Pendel in einer (sich langsam durch die Erdrotation drehenden) Schwingungsebene pendelt. Stattdessen führt es leider starke Schwingungen zur Seite hin durch, wodurch sich Ellipsenbahnen ergeben:

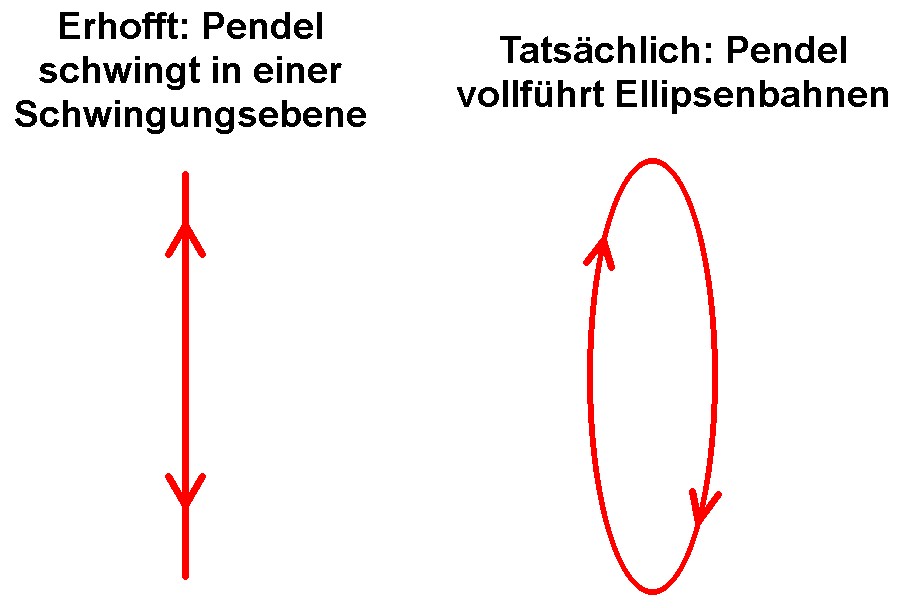
Dadurch wird eine Positionsmessung der Schwingungsebene unmöglich. Nur bei einer einzigen Messung bisher besaß das Pendel nach rund 2400 Sekunden noch (zufällig?) eine Schwingungsebene. Ich benötigte n = 139 90°-Drehungen des Schrittmotors, um den Legoarm wieder parallel zur Schwingungsebene auszurichten. Damit konnte ich die Winkelgeschwindigkeit der Drehung bestimmen.

Meine zu 0.005 °/sek berechnete Winkelgeschwindigkeit wich doch sehr deutlich vom Referenzwert (0.003 °/sek) ab. Ich kann dieser halberfolgreichen Messung aber aus obengenannten Gründen nicht trauen. Denn es kann gut sein, dass nach 2400 sek nur rein zufällig die elliptische Bahn für eine kürzere Zeit verschwand. Zumindest stimmte aber der Drehsinn der Wanderung (auf der Nordhalbkugel im Uhrzeigersinn wenn man das Pendel von oben betrachtet) 😉

Aufhängung 2: Punktlagerung

Im nächsten Schritt probierte eine Punktlagerung aus. Dazu missbrauchte ich einen Stellring…

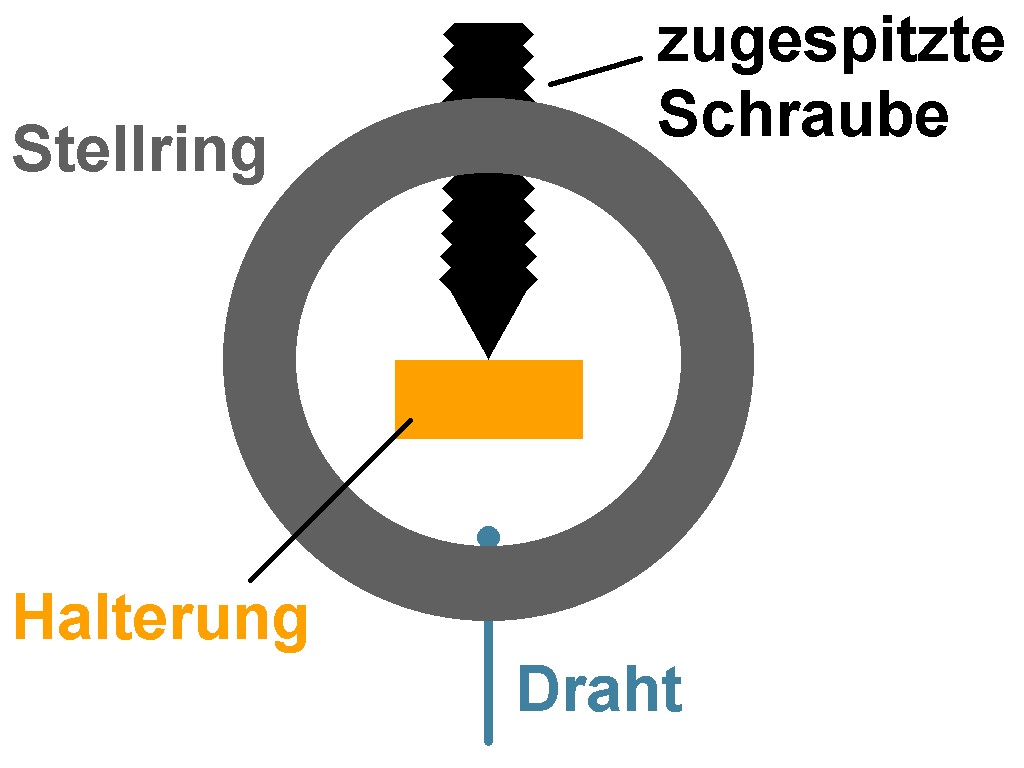
Die zugespitzte M4-Schraube:

Das Loch für den Metalldraht:

Einen zurechtgesägten Winkel benutzte ich für die Halterung. Mit zwei Holzschrauben montierte ich ihn am Türrahmen.

Die Ergebnisse waren leider extrem ernüchternd. Erstens verlor die Schwingung um einiges schneller als mit dem Nagel an Amplitude und zweitens zeigten sich die Ellipsenbahnen schon nach kürzester Zeit (1–2 min). Diese Art der Lagerung scheint also in meinem Fall total ungeeignet.

Aufhängung 3: Kugellagerung

Chatgpt schlug mir diese Art von Halterung vor: Eine Kugel liegt auf einer sehr flachen Pfanne auf.

Als sehr flache Pfanne dachte ich mir zunächst einen Hohlspiegel (konkav) verwenden zu können. Aber besitzt dieser durch die große (negative) Brennweite eine sehr geringe Krümmung, so liegt die Kugel nicht an dessen Oberfläche auf, sondern an der Lochkante. Und genau dies stellt laut Chatgpt keine gute Lagerung dar.

Auf Amazon habe ich mir jetzt einmal Messingkugeln und Messingdraht besorgt. Deshalb Messing weil ich hoffe, die Kugel dann deutlich leichter anzubohren als gehärteten Stahl und weil ich dann den Draht anlöten kann. Mal schauen, ob diese Lagerung dann besser funktioniert…

Ich habe jetzt noch einige Messungen mit der simplen Nagelaufhängung durchgeführt und damit doch recht brauchbare Resultate erzielt. Alle Wanderungen der Schwingungsebene erfolgten zum Glück auch im Uhrzeigersinn, so wie es sein sollte auf der Nordhalbkugel 😉

Hier meine beste Messung: Nach rund 3500 Sekunden musste der Schrittmotor 137 90°-Drehungen machen, um den Legoarm wieder parallel zur Schwingungsebene auszurichten.

Mit dieser 19%igen Abweichung kann ich absolut leben, zumal ja im Internet immer wieder auf die Probleme mit kurzen und leichten Foucault-Pendeln hingewiesen wird.

Kleine Anmerkung noch: Ellipsenbahnen kommen u.a. auch dadurch zustande, dass man dem Pendel beim Loslassen oft auch einen kleinen Impuls zur Seite mitgibt. Um dies zu vermeiden, sollte man das Pendel mit einem Faden auslösen, den man durchbrennt. Dies habe ich auch ausprobiert.

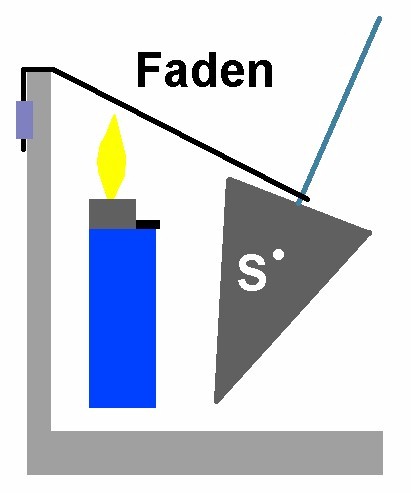
In meinem Fall funktionierte dies aber alles andere als gut. Den Faden fixierte ich außen am Schirm. Brennte ich nun den Faden mit einem Feuerzeug durch, so torkelte nach dem Start das Senklot sehr stark. Dies deshalb, weil die Verlängerung des Fadens nicht durch den Schwerpunkt ging. Ich hätte dann den besten Angriffspunkt des Fadens am Senklot herausfinden können, dies wollte ich dann aber nicht mehr. So startete ich das Pendel manuell durch bloßes Loslassen. Mit etwas Übung gelang dies eigentlich immer schon nach 5–10 Versuchen…

Ich wünsche allen Besuchern meiner Homepage ein frohes Weihnachtsfest und einen guten Rutsch ins neue Jahr und 2026 vor allem Gesundheit!

Design by ThemesDNA.com

Stoppi

Foucault-Pendel

Aufhängung 1: Nagel

Aufhängung 2: Punktlagerung

Aufhängung 3: Kugellagerung

Ich wünsche allen Besuchern meiner Homepage ein frohes Weihnachtsfest und einen guten Rutsch ins neue Jahr und 2026 vor allem Gesundheit!

Visitors