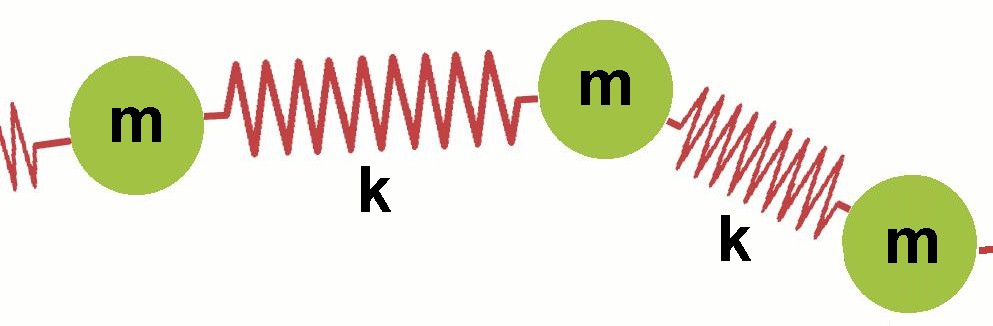
Wellen sind ja sich in den Raum ausbreitende Schwingungen. Doch von was hängt die Ausbreitungsgeschwindigkeit der Wellen ab? Elektromagnetische Wellen breiten sich im Vakuum mit der Lichtgeschwindigkeit c = 299 792 458 m/s aus. Doch wie sieht es mit Wellen in einem Festkörper aus? Um der Frage auf den Grund zu gehen, habe ich vor rund 20 Jahren eine Simulation zur Wellenausbreitung in Turbo Pascal erstellt. Das Modell besteht aus einzelnen Atomen mit der Masse m, welche miteinander über Federn mit der Federkonstante k verbunden sind. Zum Start lenke ich das erste Atom sinusförmig aus. Danach gehorchen die einzelnen Atome der Newtonschen Bewegungsgleichung F = m·a, wobei für die Kraft F das Hooksche Federgesetz F = k·Δl eingesetzt wird. Diese Differentialgleichungen habe ich mittels der Euler-Methode iterativ gelöst. Die Bewegung der Atome ist in y-Richtung eingeschränkt. Zu Beginn einzugeben ist die Anzahl der Atome, deren Masse m und die Federkonstante k. Zudem kann noch zwischen transversaler oder longitudinaler Auslenkung ausgewählt werden und ob man die Reflexion am freien oder festen Ende möchte.
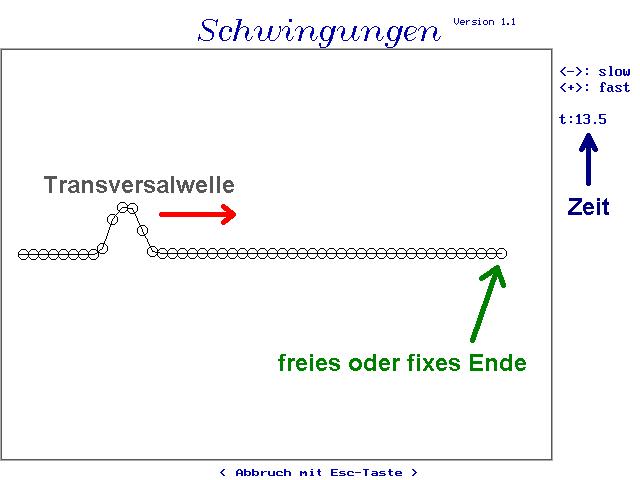
Freies oder fixes Ende beeinflusst das Reflexionsverhalten der Welle. Bei einem freien Ende wird ein Wellenberg wieder als Wellenberg reflektiert. Bei einem fixen Ende kommt ein Wellenberg als Wellental zurück.
Zur Bestimmung der Ausbreitungsgeschwindigkeit wird einfach die Zeit t notiert, bei der sich das letzte Atom ganz rechts erstmalig zu bewegen beginnt. Die Geschwindigkeit v berechnet sich dann einfach aus Pixelanzahl/Zeit t. Diese wird dann in Abhängigkeit von m bzw. k bei jeweils konstantem k bzw. m erfasst.
Wie man sieht nimmt mit zunehmender Federkonstante k die Geschwindigkeit v zu. Bei härteren Federn breitet sich also die Welle schneller aus als bei weichen Federn. Der Graph v = v(k) sieht folgendermaßen aus:
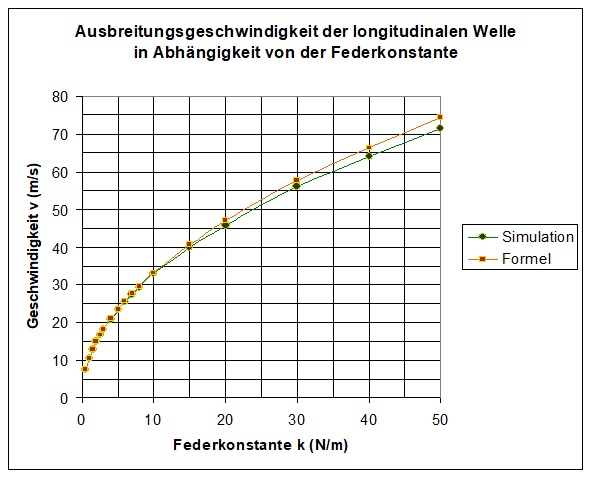
Wie sieht es bei gleicher Federkonstante k aber unterschiedlichen Massen m aus?
Hier liegt genau eine verkehrte Proportionalität vor. Je größer die Masse m der Atome, desto langsamer breitet sich die Welle aus. Steigendes m liefert also ein sinkendes v. Für den Graph v = v(m) erhält man:
Um die genaue funktionale Abhängigkeit der Geschwindigkeit v von den Größen k und m herauszufinden, geht man wiefolgt vor:
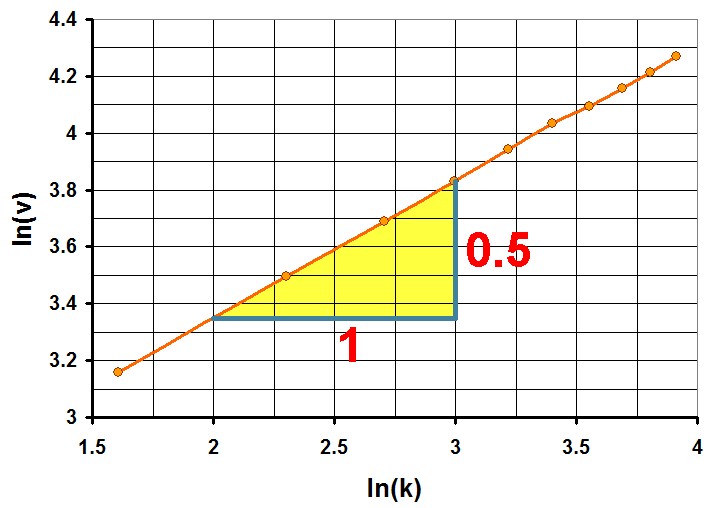
Die Potenz von k in der Formel v = v(k,m) muss daher 0.5 sein. Wie sieht es für die Potenz von m aus?
Die Potenz von m muss demnach –0.5 sein. Daher ergibt sich folgender Zusammenhang zwischen v und den Größen k und m: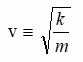
In der Literatur findet man folgende Formel für die Ausbreitungsgeschwindigkeit einer Welle in einem Festkörper: 
Anstelle der Federkonstante k tritt das Elastizitätsmodul E und anstelle der Masse m die Dichte ρ. Dies leuchtet aber auch ein. Denn das Elastizitätsmodul E ist gleich der notwendigen Kraft pro m², um einen Körper der Länge L auf seine doppelte Länge zu dehnen. Daran erkennt man die Ähnlichkeit zur Federkonstante k, welche ja der Kraft F entspricht, um die Feder um einen Meter zu dehnen. Die Zusammengehörigkeit der Masse m und der Dichte ρ ist ebenfalls offensichtlich, da ja die Dichte der Masse pro m³ entspricht.
Mit dieser einfachen Simulation haben wir also eine reale Formel zur Ausbreitungsgeschwindigkeit von Wellen hergeleitet, voila…
Das uralte Turbo-Pascal-Programm:
Program Welle;
{$N+,E+}
Uses Crt,Graph,Turbo3,Dos;
Type
Feld_1 = Array[1..150] of Real;
Var { Variablendeklaration }
vx_vorher,vy_vorher : Feld_1; { Geschwindigkeitskomponenten vorher }
vx_nachher,vy_nachher : Feld_1; { Geschwindigkeitskomponenten nachher }
sx_vorher,sy_vorher : Feld_1; { Ortskomponenten vorher }
sx_nachher,sy_nachher : Feld_1; { Ortskomponenten nachher }
m : Real; { Masse der Teilchen }
k : Real; { Federkonstante }
Force_x,Force_y: Real; { Auf die Atome wirkenden Kr„fte }
delta_t,t : Real; { Zeit und Zeitintervall }
Faktor : Real; { graphischer Darstellungsfaktor }
Amplitude,Tau : Integer; { Anregungsschwingung }
zaehler,i,j : LongInt; { Z„hlvariable }
n : Integer; { Anzahl der Atome }
l_0 : Integer; { L„nge der Federn }
max : LongInt;
GraphDriver,GraphMode : Integer;
Xgraph,Ygraph : Integer;
Maxx,Maxy : Integer;
Ch,ant,Antwort_1,Antwort_2 : Char;
Pfad: String;
Weiter,Treffer,Loeschen : Boolean;
Filename: Text;
Const
NameHeader = 'Gitter , Version 1.1';
WeiterHeader= '( weiter mit beliebiger Taste )';
Pi = 3.14159265358979323846264338327950;
g = 9.81;
Esc = #27;
Rad = (2.0 * Pi / 360.0);
Procedure WriteOut(S: String);
Begin
OutTextXY(Xgraph,Ygraph,S);
Inc(Ygraph,TextHeight('M')+4);
End;
{ÉÍÍÍÍÍÍÍÍÍÍÍÍÍÍÍ»}
{º º}
{º STARTTEXT º}
{º º}
{ÈÍÍÍÍÍÍÍÍÍÍÍÍÍÍͼ}
Procedure Starttext; { Starttext }
Begin
ClearDevice;
Setviewport(0,0,Maxx,Maxy,Clipon);
SetTextStyle(TriplexFont,HorizDir,3);
SetTextJustify(CenterText,TopText);
SetColor(14);
OutTextXY(Maxx div 2,30,'Programm zur Darstellung');
OutTextXY(Maxx div 2,50,'von Wellen');
SetTextStyle(TriplexFont,HorizDir,1);
OutTextXY(Maxx div 2,85,'von');
OutTextXY(Maxx div 2,105,'Dipl.Ing.Mag. Christoph Ernst');
SetLineStyle(SolidLn,0,ThickWidth);
Rectangle(30,20,595,145);
SetColor(15);
SetTextJustify(LeftText,TopText);
SetTextStyle(DefaultFont,HorizDir,1);
Ygraph := 210;
Xgraph := 40;
WriteOut('Anmerkung:');
WriteOut(' ');
WriteOut(' ');
WriteOut('Dieses Programm simuliert Seilwellen.Als Modell dienen');
WriteOut('mehrere Massen,welche mit den beiden Nachbarn ber Federn');
WriteOut('verbunden sind. Bei den transversalen Schwingungen wurde');
WriteOut('die Beweglichkeit der Massen eingeschr„nkt,sodaá sie sich nur');
WriteOut('in y-Richtung bewegen k”nnen. Viel Spaá mit dem Programm !');
SetColor(14);
SetTextJustify(CenterText,TopText);
OutTextXY((Maxx div 2), (Maxy-10),'<Esc> Programm beenden');
SetColor(15);
ant := Readkey;
If ant = Esc Then
Halt(1);
End;
{ÉÍÍÍÍÍÍÍÍÍÍÍÍÍÍÍ»}
{º º}
{º ABFRAGE º}
{º º}
{ÈÍÍÍÍÍÍÍÍÍÍÍÍÍÍͼ}
Procedure Abfrage;
Begin
ClearDevice;
Setviewport(0,0,Maxx,Maxy,Clipon);
SetTextStyle(TriplexFont,HorizDir,3);
SetTextJustify(CenterText,TopText);
SetColor(14);
OutTextXY(Maxx div 2,30,'Parameter-Eingabe');
SetColor(8);
SetLineStyle(SolidLn,0,NormWidth);
Rectangle(100,20,525,70);
SetColor(7);
SetLineStyle(SolidLn,0,NormWidth);
Rectangle(102,22,523,68);
SetColor(15);
SetTextJustify(LeftText,TopText);
SetTextStyle(DefaultFont,HorizDir,1);
Ygraph := 120;
Xgraph := 2;
WriteOut(' ');
WriteOut('Es mssen im folgenden von ihnen einige Parameter eingegeben werden:');
GotoXY(1,12);
Write('Wollen sie transversale (t) oder longitudinale (l) Schwingungen untersuchen? ');
Readln(Antwort_1);
Writeln(' ');
Write('Soll die Reflexion am offenen (o) oder festen Ende (f) erfolgen? ');
Readln(Antwort_2);
Writeln(' ');
Write('Anzahl der Atome [max. 125]: ');
Repeat
Readln(n);
Until (n > 0) and (n <= 125);
Writeln(' ');
Write('Masse der Atome: ');
Readln(m);
Writeln(' ');
Write('Federkonstante k in (N/m): ');
Readln(k);
Writeln(' ');
End;
{ÉÍÍÍÍÍÍÍÍÍÍÍÍÍ»}
{º º}
{º Kraft º}
{º º}
{ÈÍÍÍÍÍÍÍÍÍÍÍÍͼ}
Procedure Force(j_F,l_F: Integer;m_F,k_F: Real;x_F,y_F: Feld_1);
Var distance_links,distance_rechts : Extended;
Begin
{ Wechselwirkung zw. den Nachbaratomen }
{ ==================================== }
distance_links := SQRT((sx_vorher[j_F] - sx_vorher[j_F - 1]) *
(sx_vorher[j_F] - sx_vorher[j_F - 1]) +
(sy_vorher[j_F] - sy_vorher[j_F - 1]) *
(sy_vorher[j_F] - sy_vorher[j_F - 1]));
If (j_F < n) Then
Begin
distance_rechts := SQRT((sx_vorher[j_F] - sx_vorher[j_F + 1]) *
(sx_vorher[j_F] - sx_vorher[j_F + 1]) +
(sy_vorher[j_F] - sy_vorher[j_F + 1]) *
(sy_vorher[j_F] - sy_vorher[j_F + 1]));
End
Else
Begin
{ letztes Atom hat keinen rechten Nachbarn }
distance_rechts := l_F;
End;
If (Antwort_1 = 't') Then
Begin
{ Bei transversaler Schwingung bleiben Atome in x-Richtung fixiert! }
{ ================================================================= }
Force_x := 0.0;
End
Else
Begin
Force_x := -(distance_links - l_F) * k_F *
((sx_vorher[j_F] - sx_vorher[j_F - 1]) / distance_links) +
(distance_rechts - l_F) * k_F *
((sx_vorher[j_F + 1] - sx_vorher[j_F]) / distance_rechts);
End;
Force_y := -(distance_links - l_F) * k_F *
((sy_vorher[j_F] - sy_vorher[j_F - 1]) / distance_links) +
(distance_rechts - l_F) * k_F *
((sy_vorher[j_F + 1] - sy_vorher[j_F]) / distance_rechts);
End;
{ÉÍÍÍÍÍÍÍÍÍÍÍÍÍÍÍÍÍÍÍÍÍÍÍÍÍÍÍÍÍ»}
{º º}
{º Differenzen-Verfahren º}
{º º}
{ÈÍÍÍÍÍÍÍÍÍÍÍÍÍÍÍÍÍÍÍÍÍÍÍÍÍÍÍÍͼ}
Procedure Newton(n_sub,l_sub: Integer;delta_t_sub,m_sub,k_sub : Real;VAR x0,x1,y0,y1,vx0,vx1,vy0,vy1 : Feld_1);
Var
delta_sx,delta_sy : Extended;
j_sub : LongInt;
Begin
{ Ort- und Geschwindigkeitsindizes: 0...vorher,1...nachher }
For j_sub := 2 To n_sub Do
Begin
Force(j_sub,l_sub,m_sub,k_sub,x0,y0); { Berechnung der Kraft auf das j-te Atom}
vx1[j_sub] := vx0[j_sub] + delta_t_sub * (1.0 / m_sub) * Force_x;
vy1[j_sub] := vy0[j_sub] + delta_t_sub * (1.0 / m_sub) * Force_y;
delta_sx := (vx1[j_sub] + vx0[j_sub]) * 0.5 * delta_t_sub; { gemittelte šbergabe ! }
delta_sy := (vy1[j_sub] + vy0[j_sub]) * 0.5 * delta_t_sub; { gemittelte šbergabe ! }
x1[j_sub] := x0[j_sub] + delta_sx;
y1[j_sub] := y0[j_sub] + delta_sy;
End;
End;
{ÉÍÍÍÍÍÍÍÍÍÍÍÍÍÍÍ»}
{º º}
{º Graphik º}
{º º}
{ÈÍÍÍÍÍÍÍÍÍÍÍÍÍÍͼ}
Procedure Graphik(Loeschen_sub : Boolean);
Begin
If (Loeschen_sub) Then
Begin
{ Graphik loeschen }
{ ================ }
SetColor(0);
Circle(Trunc(sx_vorher[1]),Trunc(((maxy - 70) / 2) - sy_vorher[1]),8);
For j := 2 To n Do
Begin
Circle(Trunc(sx_vorher[j]),Trunc(((maxy - 70) / 2) - sy_vorher[j]),8);
Line(Trunc(sx_vorher[j - 1]),Trunc(((maxy - 70) / 2) - sy_vorher[j - 1]),
Trunc(sx_vorher[j]),Trunc(((maxy - 70) / 2) - sy_vorher[j]));
End;
End
Else
Begin
{ Graphik zeichnen }
{ ================ }
{
If (vx_vorher[1] >= 0) Then
Begin
SetColor(1);
Circle(Trunc(sx_vorher[1]),Trunc(((maxy - 70) / 2) - sy_vorher[1]),8);
End
Else
Begin
SetColor(2);
Circle(Trunc(sx_vorher[1]),Trunc(((maxy - 70) / 2) - sy_vorher[1]),8);
End;
}
For j := 1 To n Do
Begin
If (vx_vorher[j] = 0) Then
Begin
SetColor(3);
Circle(Trunc(sx_vorher[j]),Trunc(((maxy - 70) / 2) - sy_vorher[j]),8);
End
else If (vx_vorher[j] > 0) Then
Begin
SetColor(1);
Circle(Trunc(sx_vorher[j]),Trunc(((maxy - 70) / 2) - sy_vorher[j]),8);
End
Else
Begin
SetColor(2);
Circle(Trunc(sx_vorher[j]),Trunc(((maxy - 70) / 2) - sy_vorher[j]),8);
End;
End;
For j := 2 To n Do
Begin
SetColor(15);
Line(Trunc(sx_vorher[j - 1]),Trunc(((maxy - 70) / 2) - sy_vorher[j - 1]),
Trunc(sx_vorher[j]),Trunc(((maxy - 70) / 2) - sy_vorher[j]));
End;
End;
End;
{ÉÍÍÍÍÍÍÍÍÍÍÍÍÍÍÍÍÍÍÍ»}
{º º}
{º INITIALISIERUNG º}
{º º}
{ÈÍÍÍÍÍÍÍÍÍÍÍÍÍÍÍÍÍÍͼ}
Procedure Initialisierung; { Initialisierung s„mtlicher Parameter }
Var ErrorCode: Integer;
Begin
GraphDriver := Detect;
DirectVideo := False;
{ =============================================================== }
{ ACHTUNG : Graphik-Programme *.BGI und Schriften *.CHR mssen im }
{ Verzeichnis des auszufhrenden Programms sein !!! }
{ =============================================================== }
InitGraph (GraphDriver,GraphMode,'');
ErrorCode := GraphResult;
If ErrorCode <> grOk Then Begin
Writeln(#7,'Sorry, but I''ve a Graphics Error:');
Writeln(GraphErrorMsg(ErrorCode));
Writeln('Program intermediately stopped.');
Halt(1);
End;
SetLineStyle(SolidLn,0,Normwidth);
SetTextJustify(LeftText,TopText);
SetTextStyle(DefaultFont,HorizDir,1);
Setviewport(0,0,Maxx,Maxy,Clipon);
Maxx := Getmaxx;
Maxy := Getmaxy;
Weiter := FALSE;
End;
{ÉÍÍÍÍÍÍÍÍÍÍÍÍÍÍÍÍÍÍÍÍÍÍÍ»}
{º °°°°°°°°°°°°°°°°°°°°° º}
{º °°° HAUPTPROGRAMM °°° º}
{º °°°°°°°°°°°°°°°°°°°°° º}
{ÈÍÍÍÍÍÍÍÍÍÍÍÍÍÍÍÍÍÍÍÍÍÍͼ}
Begin
Initialisierung;
Starttext;
ClearDevice;
Abfrage;
{ ====================================== }
{ ========Initialisierung-Anfang======== }
{ ====================================== }
l_0 := Trunc((Maxx - 100) / n); { L„nge der Federn }
{ Parameter der Erregerschwingung }
{ =============================== }
If (Antwort_1 = 'l') Then
Begin
Tau := 5;
Amplitude := 10;
End
Else
Begin
Tau := 10;
Amplitude := 50;
End;
{ Startwerte der Atome }
{ ==================== }
For zaehler := 1 To n Do
Begin
sx_vorher[zaehler] := zaehler * l_0;
sy_vorher[zaehler] := 0.0;
vx_vorher[zaehler] := 0.0;
vy_vorher[zaehler] := 0.0;
End;
Weiter := False;
t := 0.0;
delta_t := 0.005;
{ ==================================== }
{ ========Initialisierung-Ende======== }
{ ==================================== }
ClearDevice;
SetViewport(0,0,Maxx,Maxy,Clipon);
SetLineStyle(SolidLn,0,NormWidth);
SetColor(14);
SetTextStyle(DefaultFont,HorizDir,1);
SetTextJustify(CenterText,TopText);
OutTextXY((Maxx div 2),470,'< Abbruch mit Esc-Taste >');
SetTextStyle(7,HorizDir,4);
OutTextXY((Maxx div 2),9,'Wellen');
SetTextJustify(LeftText,TopText);
SetTextStyle(2,HorizDir,4);
OutTextXY(455,15,'Version 1.1');
SetColor(8);
Rectangle(0,48,Maxx - 86,Maxy - 18);
SetColor(7);
Rectangle(1,49,Maxx - 87,Maxy - 19);
SetLineStyle(SolidLn,0,NormWidth);
SetViewport(2,50,Maxx - 88,Maxy - 20,Clipon);
SetColor(7);
GotoXY(71,5);
Write('<->: slow');
GotoXY(71,6);
Write('<+>: fast');
GotoXY(71,8);
Write('t:');
{ erstmalige graph. Darstellung fr Start t = 0: }
Loeschen := False;
Graphik(Loeschen);
t := t + delta_t; { Zeit-Inkrementierung }
{ =================================== }
{ ========== Zeit-Schleife ========== }
{ =================================== }
Repeat
If Keypressed Then
Begin
ant := readkey;
Case ant of
Esc : Weiter := True;
'+' : Begin
delta_t := delta_t * 2.0;
End;
'-' : Begin
delta_t := delta_t * 0.5;
End;
End; {End Case of }
End;
{ =========================================================== }
{ Ermittlung der ver„nderten Positionen und Geschwindigkeiten }
{ durch das Unterprogramm Newton }
{ =========================================================== }
Newton(n,l_0,delta_t,m,k,
sx_vorher,sx_nachher,sy_vorher,sy_nachher,
vx_vorher,vx_nachher,vy_vorher,vy_nachher);
{ ==================================== }
{ erstes Atom folgt eine halbe Periode }
{ lang einer Sinusschwingung }
{ ==================================== }
If (Antwort_1 = 't') Then
Begin
{ transversale Erregerschwingung }
{ ============================== }
sx_nachher[1] := sx_vorher[1];
vx_nachher[1] := vx_vorher[1];
vy_nachher[1] := vy_vorher[1];
If (t <= 0.5 * Tau) Then
Begin
sy_nachher[1] := Amplitude * sin(2 * Pi * t / Tau);
End
Else
Begin
sy_nachher[1] := 0.0;
End;
End
Else
Begin
{ longitudinale Erregerschwingung }
{ =============================== }
sy_nachher[1] := sy_vorher[1];
vx_nachher[1] := vx_vorher[1];
vy_nachher[1] := vy_vorher[1];
If (t <= 0.5 * Tau) Then
Begin
sx_nachher[1] := l_0 + Amplitude * sin(2 * Pi * t / Tau);
End
Else
Begin
sx_nachher[1] := l_0 + 0.0;
End;
End;
{ letztes Atom bleibt fest oder offen }
{ =================================== }
If (Antwort_2 = 'f') Then
Begin
{ festes Ende,daher unver„nderte Koordinaten }
sx_nachher[n] := sx_vorher[n];
sy_nachher[n] := sy_vorher[n];
vx_nachher[n] := vx_vorher[n];
vy_nachher[n] := vy_vorher[n];
End;
{ Bildpunkte loeschen }
{ =================== }
Loeschen := True;
Graphik(Loeschen);
{ Wertebergabe und graphische Darstellung }
{ ======================================== }
For i := 1 To n Do
Begin
sx_vorher[i] := sx_nachher[i];
sy_vorher[i] := sy_nachher[i];
vx_vorher[i] := vx_nachher[i];
vy_vorher[i] := vy_nachher[i];
End;
Loeschen := False;
Graphik(Loeschen);
GotoXY(73,8);
Write(' ');
GotoXY(73,8);
Write(t:4:2);
t := t + delta_t;
Until Weiter;
ant := readkey;
End.
Zum Abschluss noch das Youtube-Video:
