Beim Zeemaneffekt (https://stoppi-homemade-physics.de/zeeman-effekt/) habe ich beschrieben, wie es zu einer Aufspaltung der erlaubten Energieniveaus für die Elektronen in einem äußeren Magnetfeld B kommt. Bei der ESR liegen ähnliche Verhältnisse vor.

Das um den Kern “kreisende” Elektron erzeugt einen Kreisstrom mit einem magnetischen Moment µ:

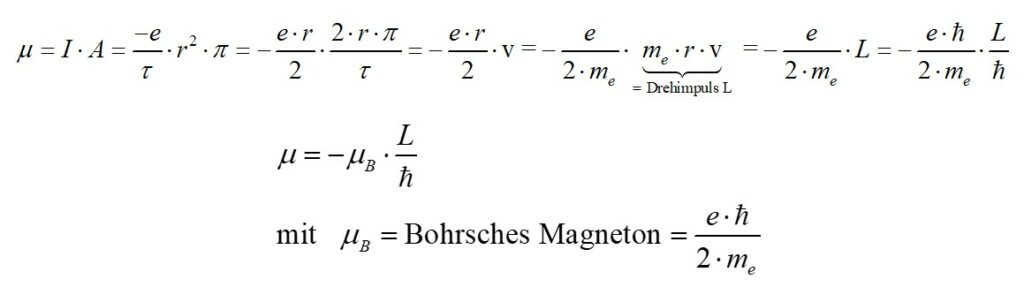
L kann nun der Bahndrehimpuls bzw. wie hier bei der Elektronenspinresonanz der Eigendrehimpuls (= Spin) des Elektrons sein.

Das äußere Magnetfeld B möchte das magnetische Moment m des Elektrons parallel zu sich ausrichten. Wie hängt dies nun mit der potenziellen Energie des magnetischen Moments im äußeren Magnetfeld zusammen?

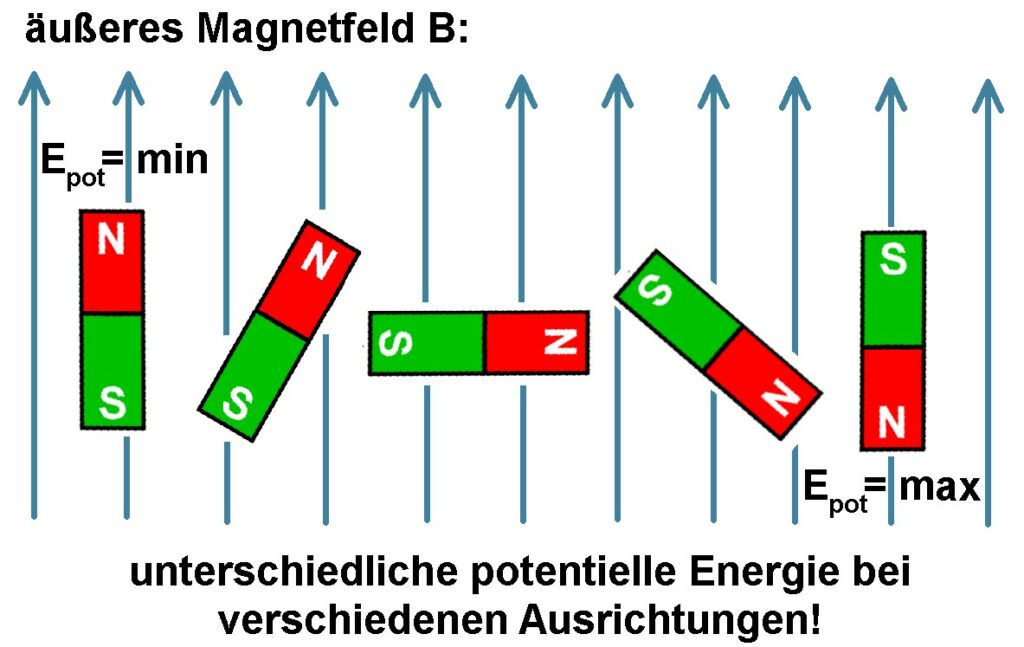
Was die potenzielle Energie betrifft so ist diese minimal, wenn das magnetische Moment in B-Richtung ausgerichtet ist (Winkel α = 0°) und maximal in entgegengesetzter Richtung (α = 180°). Die potenzielle Energie verläuft also wie die negative Cosinusfunktion. Dies führt uns zur Formel für E_pot.

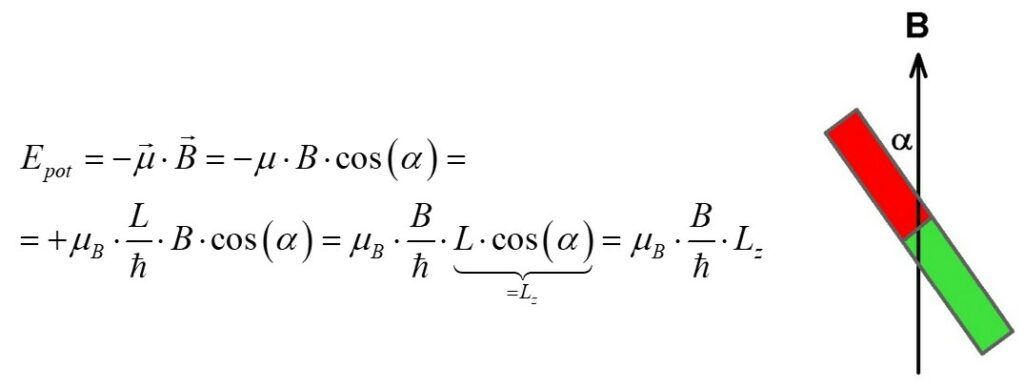
Die potenzielle Energie durch die unterschiedliche Lage des magnetischen Moments µ des Elektrons im äußeren Magnetfeld hängt also von der z-Komponente L_z des Drehimpulses ab, also jener Komponente in Richtung des Magnetfelds!

Diese z-Komponente des Drehimpulses kann beim Eigendrehimpuls des Elektrons (= Spin) nur die Werte m_s = –1/2 und +1/2 annehmen. Die möglichen potenziellen Energien sind also auch gequantelt und gehorchen folgender Formel:

Man nennt daher die Quantenzahl m_s auch magnetische Spinquantenzahl, da deren Wert wie wir gesehen haben für die Energie des Elektrons in einem Magnetfeld relevant ist!

Genau diese unterschiedliche potenzielle Energie führt in einem (äußeren) Magnetfeld also zu einer energetischen Aufspaltung der Niveaus in 2 Zustände. Wie man anhand der Formel für E_pot erkennen kann, nimmt die Energieaufspaltung linear mit der Stärke B des Magnetfelds zu. Die Termschema bei unterschiedlichen Magnetfeldern sehen dann für den Elektronenspin wie folgt aus:

Möchte man einen „Sprung“ des Elektrons von der unteren Sprosse zur oberen Sprosse bewirken, muss dem Elektron eine bestimmte Energie E_zu zugeführt werden. Diese Energie sorgt also bildlich dafür, dass sich die Orientierung des Spins umpolt.

Genau diese Energiezufuhr geschieht ja bei der Elektronenspinresonanz mit dem RF-Oszillator, welcher die Probe mit einer elektromagnetischen Welle/Energie bestrahlt. Wie groß ist nun die für diesen energetischen Sprung/dieses Umklappen des Spins notwendige Energie? Nun, hierzu müssen wir lediglich die Energiedifferenz der beiden Niveaus bilden. Diese ergibt sich zu:

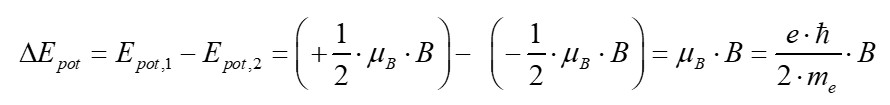
Nehmen wir an, der RF-Oszillator schwingt auf 48 MHz. Dann besitzen die Quanten der elektromagnetischen Strahlung, also die sog Photonen, nach der berühmten Formel von Max Planck die Energie

Resonanz liegt dann vor, wenn diese Photonenenergie exakt der Energiedifferent ΔE_pot entspricht.

Durch Gleichsetzung der beiden Energien kann man das Magnetfeld B ausrechnen, bei dem dann der Sprung nach oben/Resonanz erfolgt. Es gilt:

Genauso macht man es auch bei der Elektronenspinresonanz: Man erhöht kontinuierlich das Magnetfeld und schaut, wann Resonanz erfolgt. Jetzt zeigt das Experiment, dass die notwendige Flussdichte etwa die Hälfte des hier berechneten Werts beträgt. Warum ist dies so?

Nun, die bisher verwendete Formel für das magnetische Moment µ stimmt nicht ganz. Sie muss noch um einen weiteren Faktor g, das gyromagnetische Verhältnis oder auch Landé-Faktor genannt erweitert werden:

Dieser Faktor zieht sich bei den Berechnungen bis zur notwendigen Flussdichte B durch. Diese berechnet sich daher richtigerweise jetzt so:

Wie groß ist nun dieser Landé-Faktor? Für reinen Bahndrehimpuls des Elektrons beträgt g_ℓ = +1. Für reinen Spinmagnetismus und dieser Fall tritt bei der Elektronenspinresonanz auf beträgt g_s ≈ +2. Daher ergibt sich schlussendlich folgende für Resonanz notwendige Flussdichte bei einer Anregung mit 48 MHz:

Dieser Wert deckt sich nun sehr gut mit dem experimentellen Ergebnis. Man kann daher mit dem Versuch zur Elektronenspinresonanz den Landé-Faktor g berechnen und mit der Theorie vergleichen!

Der experimentelle Vorgang bei der ESR ist also folgender: Die zu untersuchende Probe befindet sich zunächst in keinem äußeren Magnetfeld (B = 0 T). Normal zum später wachsenden Magnetfeld wird die Probe mit einer elektromagnetischen Welle bestrahlt. Diese besitzt zum Beispiel eine fixe Frequenz von 48 MHz. Nun wird das möglichst homogene Magnetfeld langsam erhöht. Hierfür eignet sich ein sog. Helmholtz-Spulenpaar. Zu Beginn bei noch geringer Energieaufspaltung ist die eingestrahlte Energie des Senders zu groß für einen Sprung. Erst wenn die Aufspaltung der Energieniveaus genau jener eingestrahlten Energie entspricht (= Resonanz), absorbieren die Elektronen diese Energie und ihr Spin und damit einhergehend ihr magnetisches Moment orientieren sich neu. Steigert man das Magnetfeld weiter, so ist die Aufspaltung zu groß und die Elektronen nehmen wieder keine Energie des RF-Senders (RF steht für radio frequency) auf.

Wie stellt man nun aber fest, wann diese Resonanz vorliegt und wann nicht? Liegt Resonanz vor und der RF-Sender kann Energie an die Elektronen abgeben, so ändert sich dadurch geringfügig seine Frequenz. Genau diese Frequenzverschiebung kann man nun mit einem RTL-SDR-Dongle und entsprechender Software (z.B. mit der freeware SDRSharp https://airspy.com/download/) erfassen. Im sog. Wasserfalldiagramm weicht nun die “Linie” welche ungestört bei z.B. 48 MHz verläuft geringfügig zur Seite ab.

Bildquelle: http://www.jabolatorium.com/

Man kann den Versuch aber auch noch etwas verändern, indem man auf das wachsende Magnetfeld ein weiteres kleineres und periodisch sich veränderndes Magnetfeld moduliert. Dann “schwingt” quasi auch die Aufspaltung der Energieniveaus geringfügig mit dieser Modulationsfrequenz (z.B. 1 kHz).

Demnach gibt der RF-Sender auch bei Resonanz periodisch Energie an die Probe/Elektronen ab und die Frequenz des RF-Senders ändert sich demzufolge auch periodisch. Das mit der Antenne empfangene Radiosignal bei z.B. 48 MHz ist also mit 1 kHz moduliert. Genau diese 1 kHz-Modulation kann man nun hörbar machen. Steigert man das modulierte Hauptmagnetfeld, so hört man im Falle der Resonanz diese durch einen lauten 1 kHz-Ton. Bei zu schwachen oder zu starkem Magnetfeld hört man hingegen nichts/weniger.

Dieses Projekt zur möglichst einfachen Elektronenspinresonanz basiert auf folgender Internetseite: http://www.jabolatorium.com/

Bei professioneller ESR wird wie auch bei meinem Projekt das wachsende Hauptmagnetfeld mit einem weiteren, kleineren Magnetfeld moduliert. Der Grund ist aber nicht die “Hörbarmachung” des ESR-Signals wie bei meinem Experiment, sondern die leichtere Lagebestimmung der Resonanz.

Die periodische Modulation mit einem schwächeren Magnetfeld schlägt sich auf das ESR-Ausgangssignal durch. Dessen Amplitude ist aber nun ein Maß für die Steigung der Resonanzkurve. Befindet man sich etwa in der Flanke der Resonanzkurve, so ist dort die Steigung (erste Ableitung) groß und die Amplitude des ESR-Signals ebenfalls groß. Genau bei Resonanz ist zwar das ESR-Signal am größten, dessen Steigung aber 0! Filtert man etwa das ESR-Signal mit einem Hochpassfilter, welcher den Gleichspannungsanteil blockiert, so erhält man im Falle der Resonanz KEIN Signal! Steigert man das Hauptmagnetfeld weiter, so erhält man durch die nun abnehmende Steigung wieder ein “abgeleitetes” ESR-Signal. Man erhält also beim sukzessiven Erhöhen des Hauptmagnetfeld die blaue Signalkurve. Daraus lässt sich nun leichter als bei der roten Kurve (Anmerkung: Das Resonanzmaximum der roten Kurve ist nicht immer so schön ausgeprägt wie hier dargestellt, sondern oftmals sehr flach!) der Resonanzfall feststellen.

Nun weiter zur experimentellen Umsetzung….

Die Helmholtzspulen mit den jeweils 2 Wicklungen (Hauptmagnetfeld + Modulationsfeld) pro Elektromagnet messen bei mir 14-15 mm (Innendurchmesser). Ihr gegenseitiger Abstand muss genau dem halben Durchmesser (= Radius), also 7-7.5 mm entsprechen. Insgesamt besteht also die Helmholtzspule aus 4 Wicklungen.

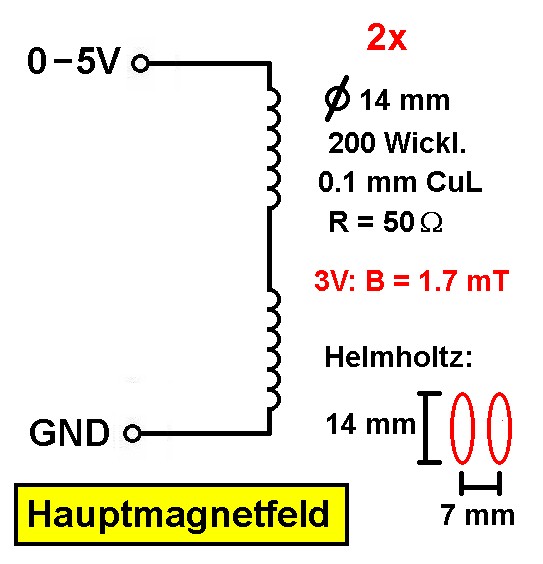
Das für das steigende Magnetfeld zuständige Spulenpaar besteht aus 200 Wicklungen mit 0.1 mm Kupferlackdraht. Dieses wird mit einem 0-5V Netzteil betrieben, wobei die Spannung händisch langsam erhöht wird. Die beiden Modulationsspulen besitzen je 50 Wicklungen ebenfalls mit 0.1 mm Kupferlackdraht. Mit dieser Konfiguration erzielt man bei einer Spannung von ca. 3 V eine magnetische Flussdichte des Hauptmagnetfelds von ca. 1.7 mT. Die Modulationsspulen werden mit einer Frequenz von ca. 1 kHz und einer Spannungsamplitude von rund 200 mV betrieben. Dadurch besitzt das Modulationsfeld eine Stärke von 0.1 mT. Umgesetzt wird diese Modulation mit dem altgedienten Timer-IC NE555 als astabile Kippstufe.

Die Stärke des Magnetfelds überprüfe ich mit dem Hallsensor MLX90290LUA-AAA-540 (https://as-electronic.net/MLX90290LUA-AAA-540). Dieser wurde mir dankenswerterweise von der Firma AS ELECTRONIC gratis zur Verfügung gestellt. Vielen herzlichen Dank dafür, habe mich sehr darüber gefreut. Seine Empfindlichkeit beträgt 100 mV/mT und der Erfassungsbereich liegt bei +/-20 mT, was sehr gut zu den angestrebten maximal 3 mT der Helmholtzspule passt.

Der RF-Sender besteht lediglich aus 2 schnellen npn-Transistoren vom Typ 2SC3355 bzw. dem 30pF-Kondensator und der RF-Spule für den Schwingkreis. Die RF-Spule ist mit 0.7 mm Kupferlackdraht gewickelt und besitzt bei 10.5 Wicklungen einen Innendurchmesser von 5 mm und eine Länge von etwa 8 mm. Ihre Induktivität liegt daher bei rund 0.339 µH. Dies ergibt eine Frequenz des Schwingkreises von ca. 50 MHz (siehe Herleitung).

Welche Probe eignet sich nun für die Elektronenspinresonanz? Idealerweise verfügt sie über ein permanentes magnetisches Moment (ungepaarte Elektronen). Bei meiner ESR greife ich auf die Substanz (Achtung Zungenbrecher!)  4-Hydroxy-2,2,6,6-tetramethylpiperidinyloxyl (4-Hydroxy-TEMPO) zurück. Dieses erhält man für rund 20 Euro auf ebay (siehe Abbildung).

Link: https://de.wikipedia.org/wiki/4-Hydroxy-2,2,6,6-tetramethylpiperidinyloxyl

Heute ist der Kupferlackdraht mit den Durchmessers 0.1 mm, 0.4 mm und 0.7 mm angekommen. Die RF-Spule war auch sehr leicht zu wickeln, da nur 10.5 Windungen. Ein passendes Plastikrohr, welches dann die zu untersuchende Probe beinhaltet und das von der RF-Spule umschlossen wird, habe ich auch in meinem Fundus entdeckt. Und die Spulenhalterungen sind auch schon im Entstehen…

Das Magnetmometer ist auch soweit fertig…

Jetzt geht es ans Wickeln der Helmholtzspule und dann messe ich das Magnetfeld aus und überprüfe dessen Homogenität. Mal schauen, ob ich nicht auf einen geringfügig dickeren Kupferlackdraht (z.B. 0.15 mm) wechseln muss.

Meine erste bei JLCPCB bestellte Platine ist angekommen:

Spaß beiseite, habe sie natürlich selbst mit dem Dremel gefertigt wie man unschwer erkennen kann 😉 Bin schon gespannt, wie sie sich bei rund 50 MHz so schlägt. Den 10 kΩ Widerstand im Ground-Pfad habe ich durch eine Serienschaltung bestehend aus 1 kΩ Festwiderstand + 10 kΩ Potentiometer ersetzt, damit ich flexibel bin. Die beiden npn-Transistoren fehlen natürlich noch….

Heute habe ich den Versuch gestartet, die Helmholtzspule zu wickeln. Was soll ich sagen? Kauft niemals einen dünnen und nur lose aufgewickelten Kupferlackdraht. Der 0.1 mm dicke Draht hat sich mehrmals verknotet und ich konnte dadurch keine einzige Spule bis zum Ende bewickeln. Hier das bildliche Dokument meines Scheiterns:

Zum Glück hatte ich zum Testen noch einen 0.3er Kupferlackdraht, welcher sich aber auch nicht auf einer Spule befand. Ich konnte damit aber zwei komplette Wicklungen mit je 100 Windungen fertigen.

Die Messungen ergaben einen Widerstand von rund 1.5 Ω und ein Magnetfeld von ca. 0.43 mT bei 0.1 A bzw. 0.15 V.

Ich habe nach dem Kupferdrahtdesaster bei conrad neuen mit 0.15 mm Dicke bestellt. Damit soll die finale Helmholtzspule aus je 200 Windungen bestehen. Verglichen mit dem 0.3er Draht hat dann jede Wicklung den 8-fachen Widerstand, also ca. 12 Ω. Um wieder eine Flussdichte von 0.43 mT zu erzeugen, wären dann durch die doppelte Windungszahl ein Strom von 0.05 A bzw. eine Spannung von 0.6 V notwendig. Da für Frequenzen um die 50 MHz Flussdichten im Bereich von 2 mT notwendig sind, benötige ich also eine Stromstärke von 0.23 A und eine Spannung von 2.79 V pro Wicklung. Da das Magnetfeld in der Helmholtzkonfiguration etwas über dem der einzelnen Spule liegt, natürlich etwas weniger Strom und eine geringere Spannung.

Hier die provisorische Helmholtzspule mit dem 0.3er Kupferlackdraht:

Bei einer Stromstärke von 0.1 A betrug die Flussdichte innerhalb der Helmholtzspule um die 0.6 mT:

Zum Thema Probe: TEMPOL scheint nicht wirklich die am besten für ESR geeignete Substanz zu sein. Um einiges besser funktioniert die ESR wohl laut dieser Homepage (https://physicsopenlab.org/2021/03/22/electron-spin-resonance-spectroscopy/) mit TTF-TCNQ (Tetrathiafulvalen  bzw. Tetracyanochinodimethan). Dieses ist etwa in älteren Elektrolytkondensatoren der Firma Sanyo konkret der Serie OS CON enthalten. Ich habe mir einmal welche aus China bestellt.

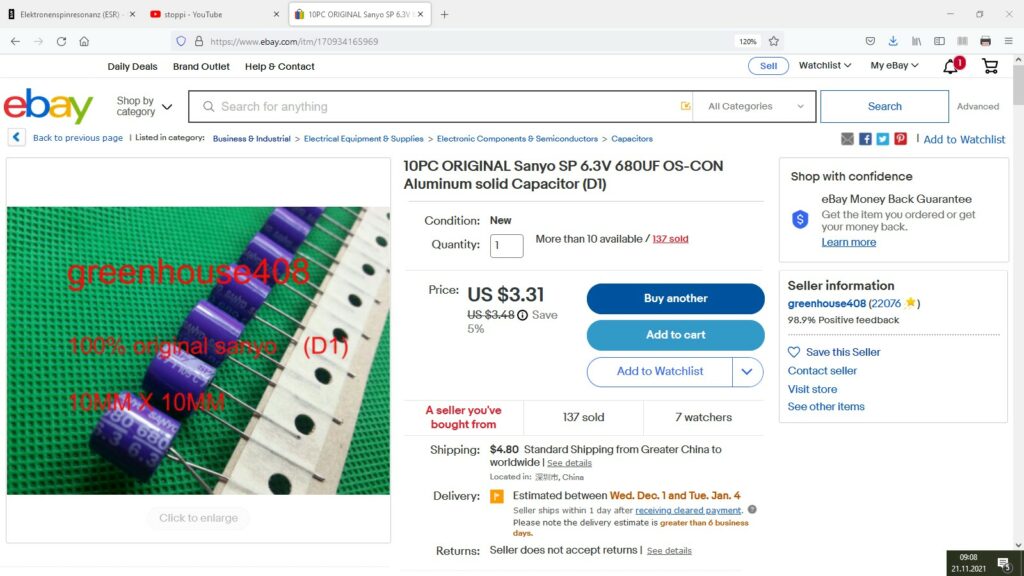
Falls ich damit scheitere werde ich wohl 2,2-Diphenyl-1-picrylhydrazyl (DPPH) hier bestellen: https://www.fishersci.de/shop/products/2-2-diphenyl-1-picrylhydrazyl-free-radical-95-2/p-7059188

250 mg für rund 50 Euro scheinen verglichen mit anderen Angeboten sehr günstig zu sein…

Ich lasse mir gerade die Spulenhalterung in 3 verschiedenen Ausführungen mit dem 3D-Drucker fertigen.

Bezugsquelle 3D-Teile: https://www.etsy.com/at/shop/MZProduction, Email: mz-production@outlook.com

Link zur Datei: https://www.tinkercad.com/things/1nMiKhj7xSq-miniesr#/

Mittlerweile sind der Kupferlackdraht und die Helmholtz-Spulenhalterungen eingetroffen und ich konnte bei zwei Stück die Modulationsspulen mit je 50 Windungen wickeln. Jetzt habe ich das Ganze einmal mit Sekundenkleber fixiert und morgen gehe ich dann die Spulen fürs Hauptmagnetfeld an. Diese haben dann je 200 Windungen. Und übrigens, der Kupferlackdraht auf den Rollen lässt sich ungleich leichter verarbeiten. Kein Knoten bisher…

Für das Hauptmagnetfeld benötigt man ja ein regelbares 0-5V Netzteil. Dieses habe ich mit dem LM317 und 3 Dioden in Serie am Ausgang umgesetzt, damit die Spannung bis runter auf 0V geregelt werden kann. Am Ausgang hängt noch ein 100 Ω Widerstand, damit die Schaltung nicht im Leerlauf läuft. Denn dann liegen am Ausgang unkontrollierte Spannungen an. Zum Einsatz kommt auch noch ein billiges 3-digit-Voltmeter.

Die Helmholtzspule ist (zum Glück) auch fertig. War eine ganz schön nervenaufreibende Angelegenheit und es sieht fertig leichter aus als es war. Erstens ist der Draht mit 0.15 mm ziemlich dünn und sensibel und zweitens sind die Abmessungen der Spule nicht gerade riesig. Sind jetzt insgesamt 4 Wicklungen zu 2 x 250 (Hauptmagnetfeld) bzw. 2 x 50 (Modulationsfeld) Windungen. Der Widerstand einer Modulationswicklung liegt bei 2.5 Ω und einer Wicklung fürs Hauptmagnetfeld bei rund 16 Ω. Die Modulationsspulen werden ja parallel verschaltet, die fürs Hauptmagnetfeld in Serie.

Im nächsten Schritt muss ich die Polaritäten der 4 Spulen mittels Hallsensor herausfinden und dann diese richtig miteinander verbinden.

So, ich habe nun die Orientierung der 4 Felder mit dem Hallsensor überprüft und die Anschlussdrähte zum Teil neu verlötet. Jetzt stimmt die Orientierung der 4 Felder und ich konnte die Hauptfeldspulen in Serie und die Modulationsspulen parallel schalten. So bekomme ich einen Spulenwiderstand von 33.2 Ω für die beiden Hauptfeldspulen und 1.4 Ω für die beiden Modulationsspulen.

Dann habe ich natürlich auch gleich geschaut, bei welcher Spannung ich welche Flussdichten zustande bringe.

Hauptmagnetfeld: 0.44 mT bei 0.72 V bzw. 1.00 mT bei 1.80 V……………………. ca. 0.58 mT/V

Modulationsfeld: 0.29 mT bei 0.39 V……………………………… 0.74 mT/V

Wenn ich mit dem Hauptfeld ca. 2 mT erreichen möchte, muss ich demnach eine Spannung von rund 3.45 V anlegen.

Das Modulationsfeld soll ca. 0.1 mT betragen. Die dafür notwendige Spannung beläuft sich dann auf 0.135 V. Beide Werte sind verglichen mit den Originalbeiträgen im Internet sehr plausibel.

Die Helmholtzspule muss ja für das Experiment noch kalibriert werden, sprich ich muss wissen, wieviel Millitesla einem Volt entsprechen. Dazu habe ich eine Messreihe aufgenommen. Der erhaltene Graph ist nahezu perfekt linear und weist eine Steigung von 0.5843 mT/V auf. Diesen Wert benötige ich dann später für die Berechnung des Landefaktors g.

Die speziellen Elektrolytkondensatoren der Firma Sanyo sind angekommen. Sie enthalten ja das für die ESR besonders geeignete Tetrathiafulvalen  bzw. Tetracyanochinodimethan (kurz TTF-TCNQ).

Im nächsten Schritt zerlegte ich die Kondensatoren, um an das TTF-TCNQ zu gelangen. Dieser Schritt erfolgte aus Sicherheitsgründen mit Handschuhen und FFP2-Maske!

Die einzelnen dünnen Platten sind die Aluminiumfolien und der gesuchte Elektrolyt das schwarze, graphitähnliche Pulver bzw. die schwarzen Plättchen darauf. Dieses/diese habe ich mit einem Bastelmesser vom Träger abgekratzt und dann in das Probenröhrchen gefüllt. Zum Abschließen der Probe verwende ich Plastilin. Zuvor wurde die Probe noch mit einem abgeschnittenen Zahnstocher verdichtet.

Hier nun die fertige Probe:

Meine Weihnachtsgeschenke sind schon heute aus Fernost eingetroffen. Für das ESR-Projekt waren die HF-Transistoren 2SC3355 und der RTL-SDR USB-Stick dabei 🙂

Heute habe ich die Modulationsschaltung an die Modulationsspule angeschlossen und den Spannungsverlauf überprüft. Ohne angeschlossener Spule erhalte ich bei Verwendung eines 100 µF Kondensators eine Spannungsamplitude von knapp über 100 mV, mit einem 47 µF Kondensator steigt diese auf 220 mV.

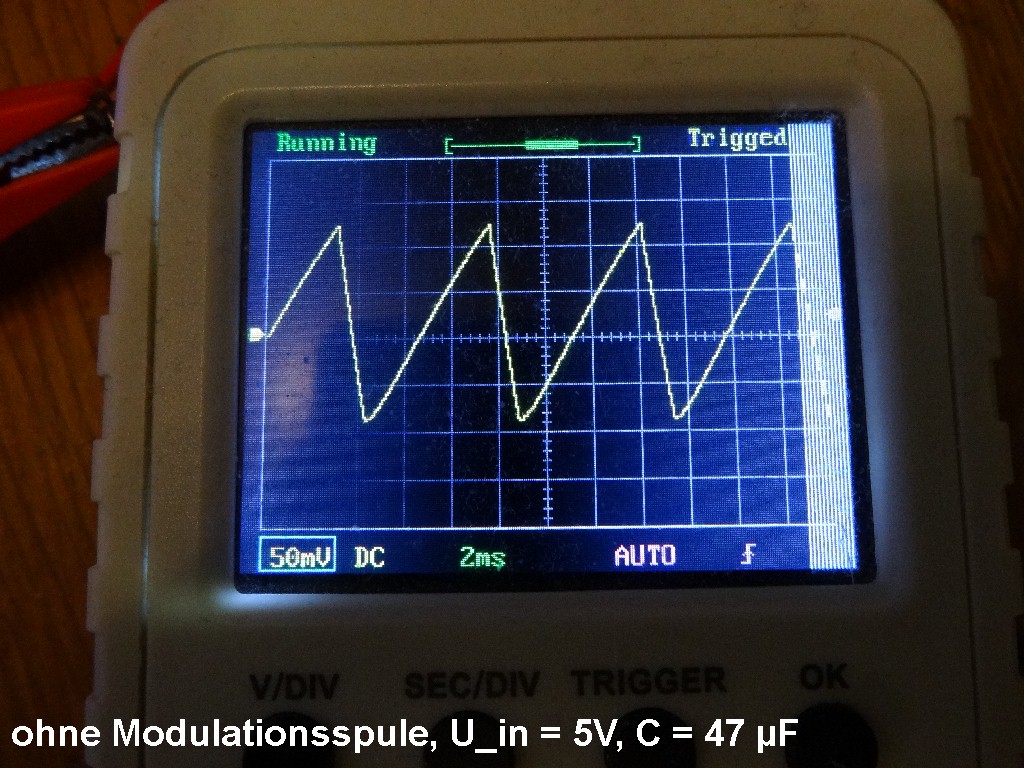
Schließe ich die Modulationsspule an, geht die Spannung in den Keller und erreicht bei einer Versorgungsspannung von 5V nur noch eine Amplitude von 14 mV und bei 10 V eine Amplitude von 38 mV. Die Kapazität ob 47 µF oder 100 µF hat keinen Einfluss mehr auf den/die Spannungsverlauf/amplitude. Ob diese geringe Spannung für die Modulation ausreicht wird sich zeigen. Eigentlich bräuchte ich eine Spannung von ca. 130 mV um eine gewünschte Flussdichte von 0.1 mT mit der Modulationsspule zu erzielen…

Dank der eingetroffenen Transistoren konnte ich auch den HF-Oszillator fertigstellen. Dieser schwingt eigentlich sehr schön bei 47.3 MHz (siehe Signal mit SDRsharp). Die Frequenz reagiert auch deutlich auf Verstellung des 10 kΩ Potentiometers bzw. wenn ich meine Hand der Spule nähere.

Da die Modulationsschaltung mit dem NE555 nicht zufriedenstellend lief (zu niedrige Frequenz im Bereich von 250 Hz und zu niedrige Spannungsamplitude von nur 14 mV bei 5V Versorgungsspannung) habe ich mich noch einmal der Sache angenommen.

Zuerst tauschte ich den NE555 gegen einen TLC555. Die Probleme blieben bestehen, Amplitude und Frequenz waren weiterhin viel zu niedrig. Dann habe ich es mit einem neuen NE555 probiert und siehe da, die Frequenz ist nun bei 5V auf 650 Hz gestiegen. Bei 12V sind es dann rund 1.3 kHz. Und die Amplitude (genauer V_pp) beträgt bei 5V genau 28 mV und erhöht sich auf 100 mV bei 12V Versorgungsspannung. Das sind doch gleich viel bessere Werte 🙂

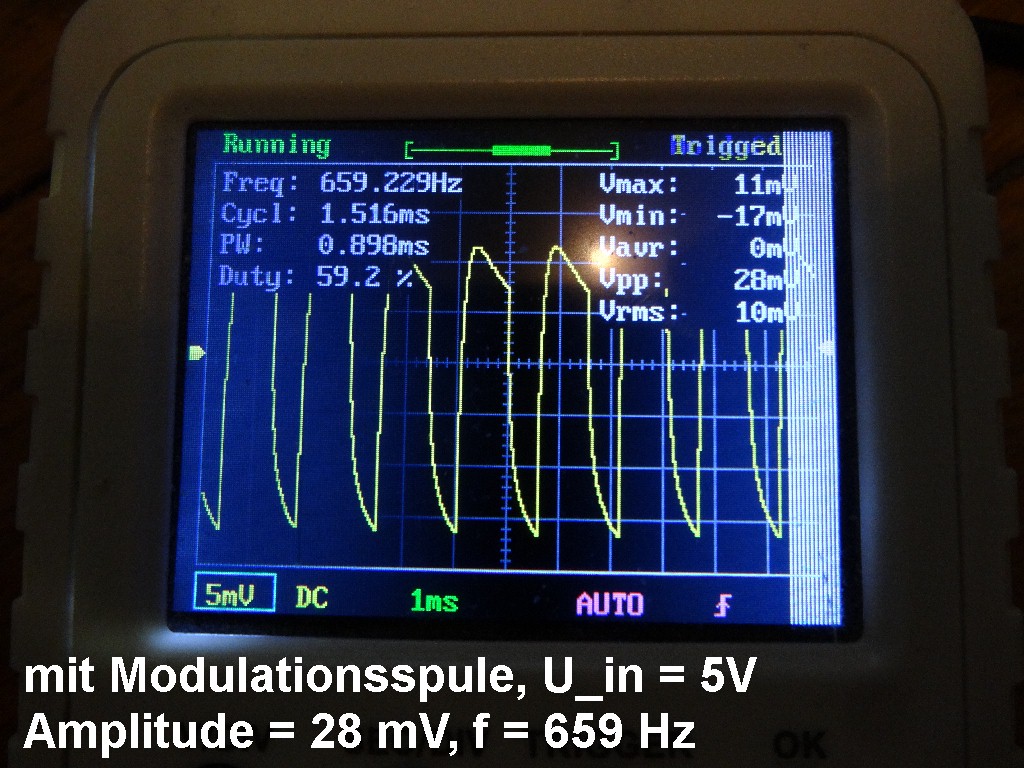
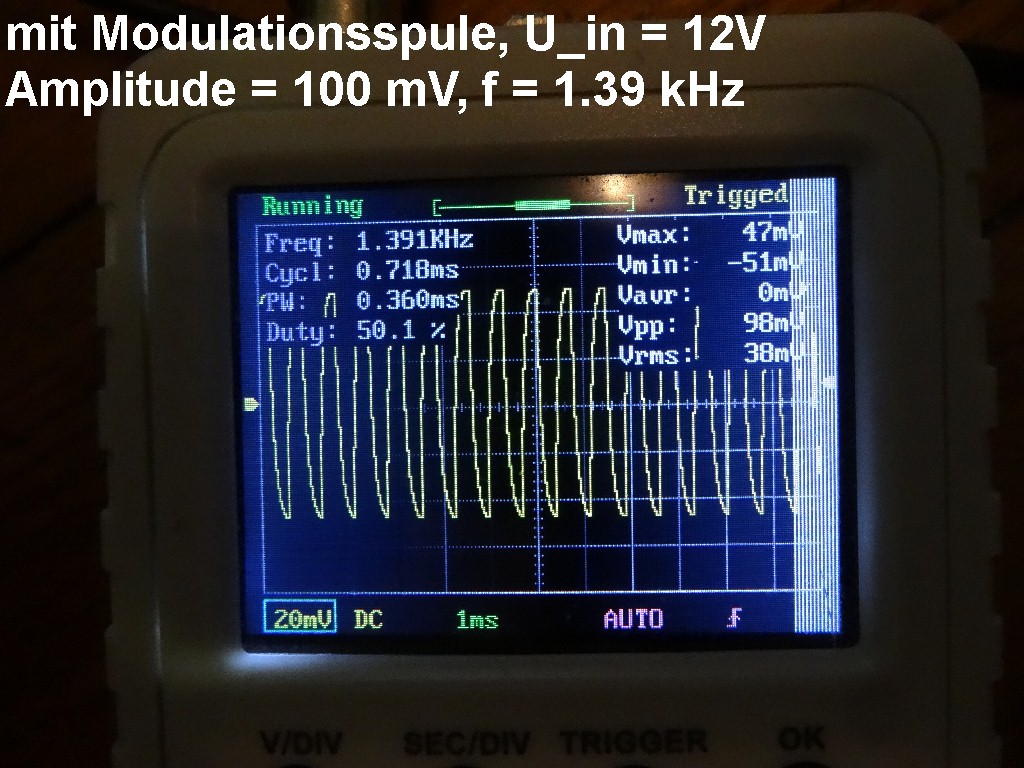
Um mit der Modulationsspule 0.1 mT zu erzielen, sind rund 130 mV notwendig. Ich werde daher den NE555 mit 12V betreiben, das müsste dann auch (fast) passen. Obwohl, dann sind die 1.39 kHz wiederum zu hoch. Denn eigentlich müsste die Frequenzmodulation des ESR-Signals dann ja sogar 2 · 1.39 kHz betragen, da ja dann pro “Schwingung” zweimal Resonanz erfolgen müsste. Und dann wäre ich bei einem hörbaren Ton von 2.78 kHz. Ich werde daher die Kapazitäten der Timerschaltung abändern.

Die Schaltung habe ich dann auch gleich mit LTSpice simuliert. Jetzt stimmen Theorie und Experiment zum Glück schon deutlich besser überein:

Heute habe ich den Frequenzbestimmenden Kondensator der Modulationsschaltung gegen einen mit 22 µF (vorher 10 µF) getauscht. Jetzt erhalte ich bei einer Versorgungsspannung von 12V eine Frequenz von 610 Hz und eine Spannungsamplitude von 111 mV. Mit diesen Werten bin ich sehr zufrieden.

Hier noch einmal die nun aktualisierten Schaltpläne:

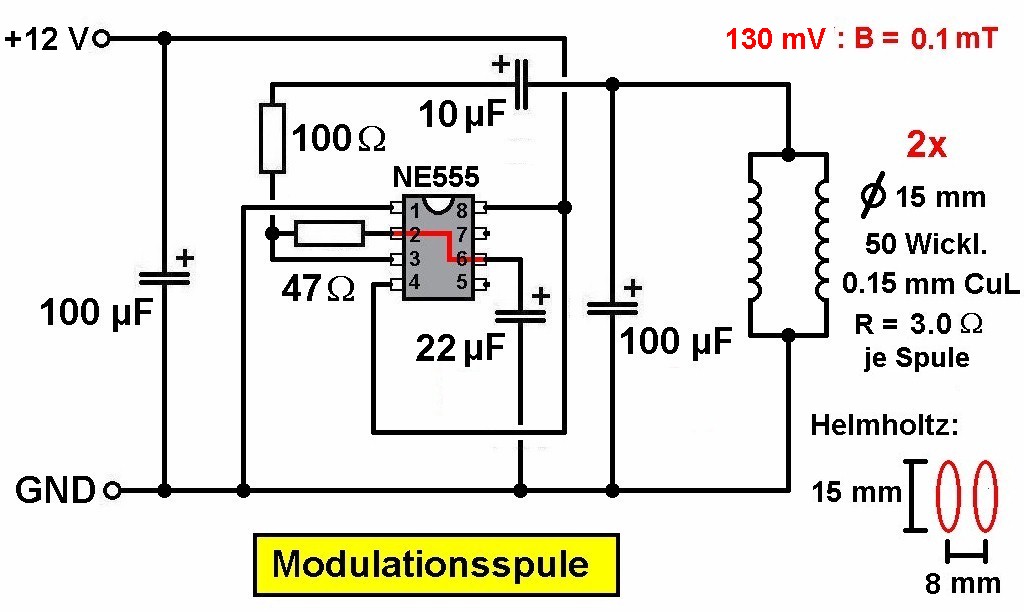
Jetzt baue ich einmal alles schön auf und danach kann ich eigentlich den ersten Testlauf starten. Bin schon sehr gespannt, ob ich etwas messen kann.

Heureka…

Habe heute den ersten Test gestartet. Zuerst einmal konnte ich nichts detektieren. Das HF-Signal war auch ziemlich breit. Deshalb tauschte ich das sicherlich Störungen verursachende 12V-Schaltnetzteil gegen einen 12V Li-Ionen-Akkupack aus und siehe da, das Frequenzspektrum war deutlich schmäler.

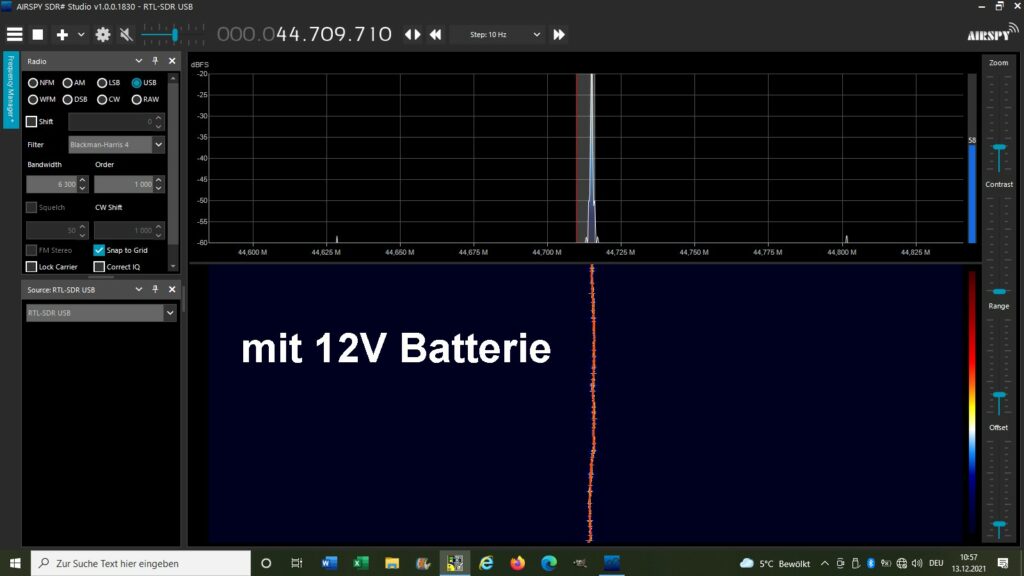
Dann testete ich den Aufbau zunächst ohne Modulation. Da konnte ich aber leider keine Verschiebung des Peaks beobachten. Um die Spulenspannung und damit das Magnetfeld feinfühliger einstellen zu können, tauschte ich das normale Potentiometer gegen ein 10-Gang-Poti aus. Aber auch damit konnte ich keine Resonanz finden. Daher schaltete ich nun das Modulationsfeld hinzu. Und siehe da bzw. besser gesagt höre, ich konnte bei Veränderung der Spulenspannung einen immer lauter werdenden und dann wieder leiser werdenden Ton wahrnehmen. Die maximale Lautstärke erzielte ich bei 2.72 V Spulenspannung.

Zur Überprüfung tauschte ich den 22 µF Kondensator der Modulationsschaltung gegen einen mit 10 µF aus. Dadurch verdoppelte sich ca. die Modulationsfrequenz. Und der hörbare Ton besaß wie zu erwarten war auch die doppelte Tonhöhe. Die Lage des Maximums blieb aber konstant…

Mit diesem Wert habe ich dann den Lande-Faktor berechnet. Der HF-Oszillator schwingte auf einer Frequenz von 44.575 MHz. Im Frequenzspektrum oben bzw. Wasserfallspektrum unten von SDRsharp konnte ich bei Resonanz deutlich Nebenpeaks um die zentrale Frequenz (eben 44.575 MHz) beobachten. Der damit berechnete Lande-Faktor belief sich auf g = 2,00455. Zum Vergleich der Tabellenwert: g = 2,002319…

Ich glaube, so genau habe ich noch keine Konstante bisher experimentell bestimmen können. Jetzt werde ich den Aufbau noch ein wenig umgestalten, aber ich bin überglücklich dass das Experiment zumindest teilweise auf Anhieb funktioniert hat. Warum ich allerdings ohne Modulationsfeld keine Resonanz/Frequenzverschiebung feststellen konnte, ist mir im Moment noch unklar. Jabolatorium hat in seinem Wasserfallspektrum einen deutlichen Ausschlag erhalten…

Fühle mich aber trotzdem gerade wieder wie Robert Millikan bei seiner Entdeckung der Elementarladung oder eben Archimedes in der Badewanne 😉

Der Aufbau ist soweit fertig. Fertige ESR-Aufbauten für Schule oder Universität gibt es auch zu kaufen. Allerdings kosten diese rund 2000 Euro. Meiner kostete mich nur rund 100 Euro inkl. 3D-Druck.

Ich habe heute noch versucht, die Resonanz auch ohne Modulationsfeld zu erfassen. In SDRSharp ist im Resonanzfall eine leichte Beule im Wasserfalldiagramm zu erkennen.

Mit Modulationsfeld hört man im Resoanzfall relativ deutlich den Modulationston. Dieser ist bei einer Spannung zwischen 2.66 und 2.72 V am lautesten. Schön sieht man dann auch im Frequenzspektrum die FM-Seitenbänder bei den Frequenzen f_Träger ± n · f_Modulation rund um die Trägerfrequenz.

Das fertige Youtube-Video binde ich hier natürlich ein. Großer Dank nochmals an Jabolatorium (http://www.jabolatorium.com/) für sein großartiges ESR-Projekt…

Zum Abschluss noch die finanzielle Abrechung dieses Projekts und das Youtube-Video: