
Bildquellen: https://de.wikipedia.org/wiki/Charles_Fabry, https://de.wikipedia.org/wiki/Alfred_P%C3%A9rot
Das Fabry-Pérot-Interferometer wurde 1897 von den französischen Physikern Charles Fabry (1867-1945) und Alfred Pérot (1863-1925) entwickelt. Es ist ein optischer Resonator, der aus zwei teildurchlässigen Spiegeln gebildet wird. Ist der Spiegelabstand unveränderbar (bspw. bei einem Glas mit auf beiden Seiten aufgedampften Spiegeln), so werden diese Aufbauten als Fabry-Pérot-Etalon bezeichnet. Ein eintreffender Lichtstrahl wird nur dann durch diesen Aufbau geleitet (transmittiert), wenn es zu einer konstruktiven Interferenz (Wellenberg auf Wellenberg) kommt, also eine bestimmte Resonanzbedingung erfüllt ist.
Damit lässt sich das Fabry-Pérot-Interferometer u. a. als optischer Filter einsetzen, der aus einer breitbandigen Strahlung bestehend aus vielen Wellenlängen ein schmalbandiges Spektrum bestehend aus nur wenigen Wellenlängen bzw. einer Wellenlänge herausfiltert. Spiegelverschiebungen ermöglichen es darüber hinaus, die spektralen Eigenschaften der transmittierten Strahlung einzustellen, da sich ja bei verändertem Spiegelabstand L die Resonanzbedingung verändert!
1. Fall: Einfallswinkel α = 0, d.h. senkrechter Lichteinfall
Hier muss man zwei Fälle unterscheiden:
a.) Die Wellenlänge λ bleibt gleich und die Länge L des Zwischenraums ändert sich
 Es tritt immer dann konstruktive Interferenz auf, wenn folgende Bedingung erfüllt ist: 2 · L = n · λ. Wächst also L, so erhält man immer bei ganzzahligen Vielfachen der Wellenlänge eine konstruktive Interferenz und die Transmission durch das Fabry-Perot-Interferometer ist maximal.
Es tritt immer dann konstruktive Interferenz auf, wenn folgende Bedingung erfüllt ist: 2 · L = n · λ. Wächst also L, so erhält man immer bei ganzzahligen Vielfachen der Wellenlänge eine konstruktive Interferenz und die Transmission durch das Fabry-Perot-Interferometer ist maximal.
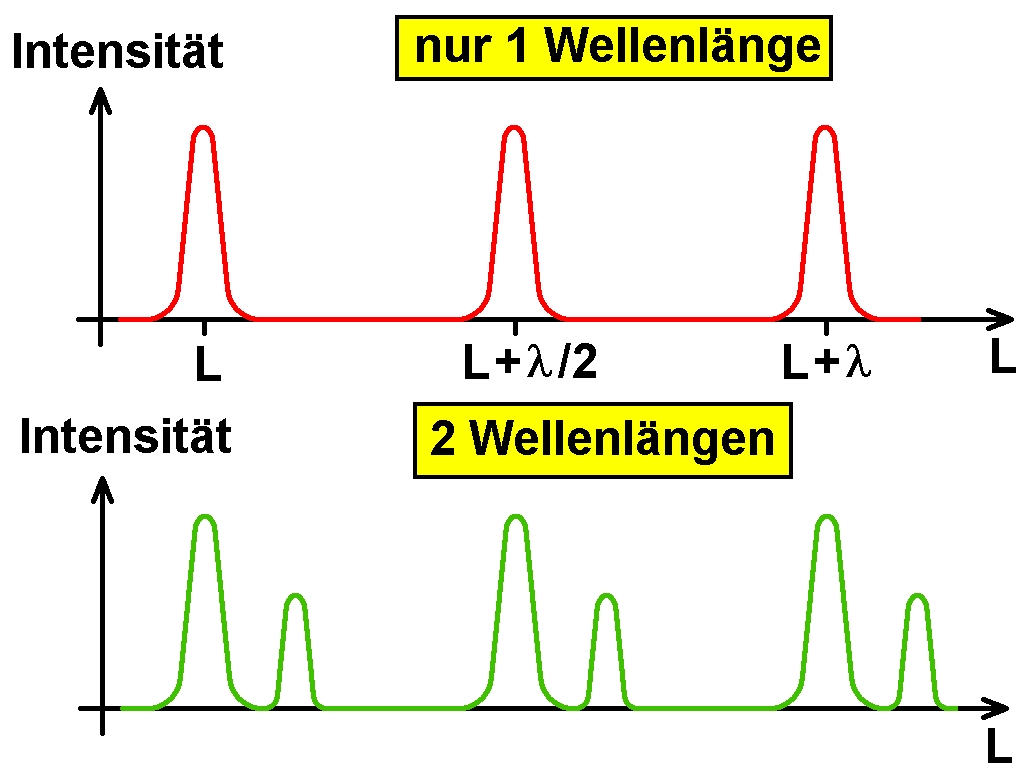
Besteht die Lichtquelle zum Beispiel aus 2 unterschiedlichen Wellenlängen, so erhält man bei sich ändernder Länge L das zweite Intensitätsmuster. Auf diese Weise können zum Beispiel die einzelnen Moden eines Lasers untersucht werden.
Für einen Wechsel von einer konstruktiven Interferenz zur nächsten ist wie oben angeführt eine Änderung des Zwischenraums von genau λ/2 notwendig. Im sichtbaren Spektralbereich geht es hier also um Verschiebungen im Bereich von 300 nm! Wie kann man solch kleine Verschiebungen umsetzen?
Eine Möglichkeit ist es einen Piezokristall zu verwenden. Solche findet man zum Beispiel in Piezo-Tongeneratoren (Summer). Drückt man einen Piezokristall zusammen, so kommt es durch die Verschiebung der Ladungsschwerpunkte zu einer sog. Piezospannung. Diese kann im Bereich von Hochspannung liegen, wenn man nur an die Piezozünder in Feuerzeugen denkt. Legt man umgekehrt eine Spannung an einen Piezokristall, so ändert er seine Geometrie (sog. Elektrostriktion). Genau dies benötigen wir hier. Dazu habe ich einfach in einen Piezosummer mittig ein Loch gebohrt.


Die Intensität des durch das Fabry-Perot-Interferometer gehenden Laserstrahls wird mit einer Photodiode + Transimpedanzverstärker (TIA) gemessen.
b.) Die Wellenlänge λ ändert sich und die Länge L des Zwischenraums bleibt gleich
Diesen Fall benötigt man, wenn man das Fabry-Perot-Interferometer als Farbfilter benutzen möchte. Für den Fall konstruktiver Interferenz gilt wiederum die Bedingung: 2 · L = konstant = n · λ
Ob nun eine bestimmte Farbe durch das Interferometer gelangt oder nicht, hängt eben von dieser Interferenzbedingung ab. Ist sie erfüllt, so kann die konkrete Wellenlänge λ das Fabry-Perot-Interferometer passieren, anderenfalls nicht. Man erhält also nur für bestimmte Wellenlängen bzw. Frequenzen konstruktive Interferenz bzw. eine hohe Transmission. Wie weit liegen nun diese Wellenlängen/Frequenzen auseinander? Hierzu folgende Herleitung:
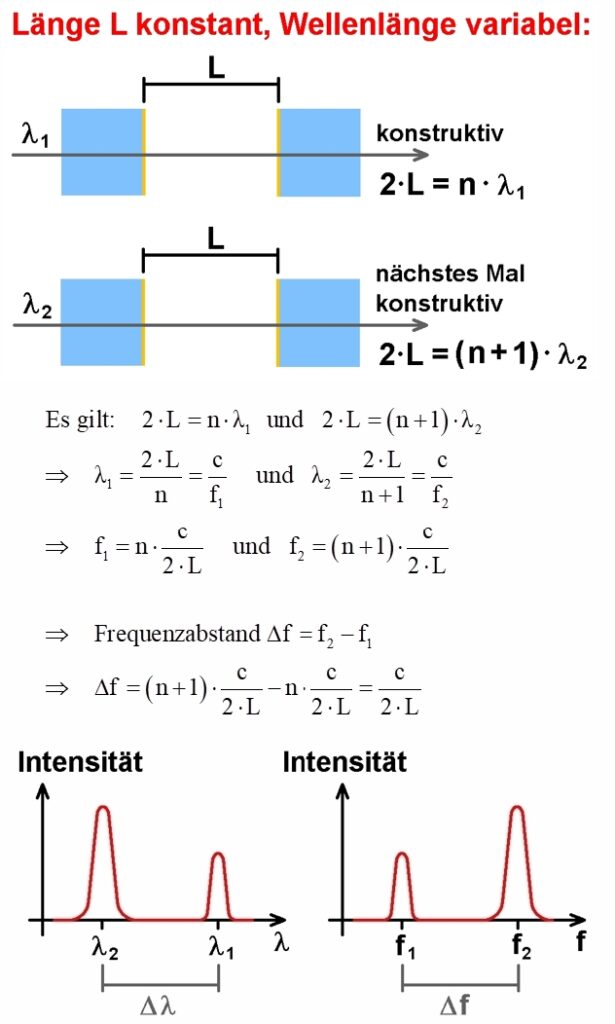
Die “erlaubten” Frequenzen unterscheiden sich also immer um c / (2·L). Dies bedeutet etwa, dass die erlaubten Frequenzen umso näher beisammen sind, je länger der Zwischenraum des Fabry-Perot-Interferometers ist.
Welche Spiegel nimmt man nun für dieses Interferometer. Nehmen wir einmal an, die Oberflächenspiegel besitzen ein Reflexionsvermögen von 95% (R = 0.95). Dies bedeutet, dass nur 5% des einfallenden Lichts überhaupt in den Zwischenraum des Interferometers gelangt. Beim Durchtritt des “ersten” Strahls durch den zweiten Spiegel sinkt die Intensität noch einmal auf 5% ab. Es bleibt also nur mehr eine Intensität von 0.05 · 0.05 = 0.0025 ∼ 0.25%. Zwar steigert sich durch die “zweiten” und “dritten” usw. Strahlen die Intensität ein wenig, aber in Summe wird mit einer sehr geringen Intensität zu rechnen sein. Bei Verwendung eines Lasers mit zum Beispiel 100 mW, erhält man nur mehr rund 0.25 mW am Ausgang.
Jetzt könnte man vorschlagen, Spiegel mit geringerem Reflexionsgrad zu verwenden, z.B. mit R = 0,5. Dadruch steigert sich natürlich die Intensität des durchgehenden Laserstrahls. Aber dies hat auch einen entscheidenden Nachteil. Je niedriger das Reflexionsvermögen, desto breiter und flacher werden die Intensitätsprofile. Ein Maß für die Schärfe der Intensitätsmaxima ist die sog. Finesse. Je höher diese ist, desto schärfer ist das Interferenzmuster bzw. die Intensitätsprofile. Nun nimmt mit abnehmenden R die Finesse F ebenfalls ab, wie man anhand folgender Abbildung sehr schön erkennen kann:

Bildquelle: https://www.thorlabs.com/newgrouppage9.cfm?objectgroup_id=9021
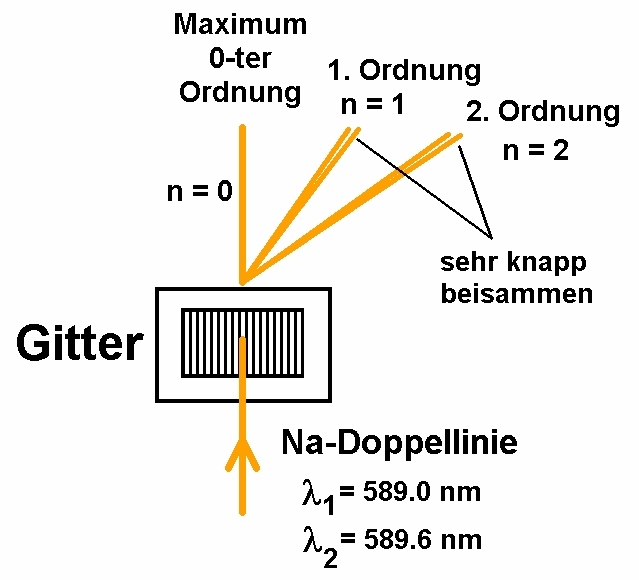
Eine Anmerkung noch zum Auflösungsvermögen eines Fabry-Perot-Interferometers. Bei einem Beugungsgitter liegen ja die Maxima von zwei nahezu identischen Wellenlängen (zum Beispiel die Natrium-Doppellinie mit λ = 589 nm und λ = 589.6 nm) extrem nahe beisammen. Dies ist dadurch begründet, dass für das Maximum 1-ter Ordnung ein Gangunterschied von nur 1·λ vorliegt, für das Maximum 2-ter Ordnung entsprechend von nur 2·λ usw.
Wie sieht es aber beim Fabry-Perot-Interferometer aus? Nun hier ist der Abstand L der beiden Spiegel viel, viel größer als die Wellenlänge des Lichts. L beträgt zum Beispiel 3 mm und λ = 589 nm = 0.000589 mm. Welche Auswirkungen hat dies aber nun auf die Lage der Maxima? Durch den großen Abstand L kann es nun selbst bei minimalen Unterschieden der Wellenlänge zu allen möglichen Phasenverschiebungen zwischen 0° (konstruktive Interferenz), 180° (destruktive Interferenz) und 360° (wieder konstruktive Interferenz) kommen. Ist L zum Beispiel gerade so groß, dass für die eine Natriumlinie mit λ = 589 nm konstruktive Interferenz vorliegt, so können für die zweite Natriumlinie nun prinzipiell alle möglichen Phasen auftreten. Dies ist dadurch begründet, dass beim Fabry-Perot-Interferometer im Gegensatz zum Gitter nicht niedrige Ordnungen (n = 0, 1, 2 …) vorkommen, sondern extrem hohe. Bei L = 3 mm und λ = z.B. 600 nm beträgt die Ordnung quasi bereits n = 10000. Beträgt etwa der Wellenlängenunterschied nur 0.6 nm, so macht dies bei n = 10000 bereits 6000 nm aus, was ja bei λ = 600 nm bereits wieder 10 vollen Wellenlängen entspricht! Deshalb kann bei Vergrößerung des Zwischenraums L das Maximum der zweiten Linie prinzipiell überall zwischen den peaks der ersten Wellenlänge liegen und muss nicht dermaßen knapp bei der ersten Linie liegen wie beim Beugungsgitter.


2. Fall: Einfallswinkel α > 0, d.h. schräger Lichteinfall
Wie sehen nun die Verhältnisse bei schrägen Lichteinfall aus? Hier eine entsprechende Skizze:

Der Wegunterschied Δs der miteinander interferierenden Strahlen beträgt also 2 · L · cos(α). Mit zunehmenden Einfallswinkel α ändert sich also der Wegunterschied Δs. Bestrahlt man also das Fabry-Perot-Interferometer schräg mit monochromatischen Licht, so kommt es abhängig vom Einfallswinkel α zu konstruktiver oder destruktiver Interferenz. Liegen gleichzeitig viele verschiedene Einfallswinkel α vor, so erhält man mehrere Intensitätsmaxima und -minima in Form von konzentrischen Kreisen.

Bildquelle: https://de.wikipedia.org/wiki/Fabry-P%C3%A9rot-Interferometer
Das oben Angesprochene bzgl. der Lage der Maxima von auch eng beisammen liegenden Spektrallinien gilt natürlich auch hier bei schrägem Einfall. So kann es sein, dass sich die zweite Natrium-D-Linie genau zwischen zwei Maxima der ersten immer befindet. Oder aber, sie liegen enger beisammen. Es würde auch möglich sein, dass zufälligerweise die Ringe beider Spektrallinien genau aufeinander liegen. Aber im Gegensatz zur Beobachtung beim Beugungsgitter, wo die beiden Linien zwingend extrem nahe beisammen liegen, ist hier beim Fabry-Perot-Interferometer der Abstand zueinander beliebig.

Zum Abschluss der ganzen Erläuterungen ein echtes Interferometer der Natrium-Doppellinie:

Bildquelle: http://hyperphysics.phy-astr.gsu.edu/hbase/phyopt/fabry2.html
Experiment:
Wie immer versuche ich auch hier eine möglichst einfache und kostengünstige, experimentelle Umsetzung. Fabry-Perot-Etalons kosten gut und gerne einmal 1500 Euro. Ich werde es mit Oberflächenspiegel á 5 Euro probieren. Hierzu habe ich Oberflächenspiegel mit ca. 95%igen Reflexionsgrad und dann mit nur 50%igen Reflexionsgrad bestellt.
Günstige Bezugsquelle: https://astro-didaktik.de/astromedia/lenses-mirrors-foils/mirror.html
Als monochromatische Lichtquelle werde ich einen roten Laser verwenden. Zur Verfügung hätte ich einen starken mit rund 200 mW und dann noch die günstigen 5mW-Module. Bei Verwendung der 50% teildurchlässigen Spiegel könnte es auch sein, dass die schwache Variante ausreichend ist, mal schauen.

Sämtliche Halterungen für Spiegel, Photodiode und Laser bestehen aus Aluminium und besitzen die Abmessungen 50 x 50 x 3 mm:

Das Gerüst des Interferometers ist soweit fertig. Ich habe einmal ein 6 mm Loch für den 5 mW Laser und ein 5 mm Loch für die Photodiode SFH203 gebohrt. Wenn der Laser zu schwach sein sollte, bohre ich das Loch für den 200 mW Laser noch auf. Jetzt warte ich einmal auf die Oberflächenspiegel bzw. teildurchlässigen Spiegel. Ich habe 2 idente Aufbauten gebastelt, da ich mit einem die Lasermoden durch Längenveränderung mit dem Piezosummer erfassen möchte und mit dem anderen die konzentrischen Kreise, welche ja typisch sind für das Fabry-Perot-Interferometer.






Als monochromatische Lichtquelle für den zweiten Aufbau kommt entweder ebenfalls ein Laser zum Einsatz, oder meine Natrium-Dampflampe.





Mit dem ersten Aufbau möchte ich ja die Wellenlänge/Moden eines Lasers bestimmen. Hierzu verändere ich mittels Piezosummer die Länge L des Spalts zwischen den beiden Spiegeln. Beim zweiten Aufbau möchte ich die für das Fabry-Perot-Interferometer typischen konzentrischen Ringe erzeugen. Für diesen Aufbau fällt also der Laser, die Piezoscheibe und die Photodiode weg. Stattdessen postiere ich vor dem Interferometer einen Kollimator mit f = 156.4 mm und 40 mm Durchmesser (auch über PGI-Skarabäus erhältlich).



Heute sind die Oberflächenspiegel, die halbdurchlässigen Spiegel und die Federringe eingetroffen. Die Federringe kommen auf die M4-Gewindestange in den Zwischenraum der beiden Spiegel. Damit hoffe ich, den Spiegelabstand L stabil verändern zu können.





Gestern konnte ich entscheidende Fortschritte erzielen. Zuerst habe ich die beiden teildurchlässigen Spiegel (R = 0.5) auf die Trägerplatte geklebt. Dazu verwendete ich gewöhnliches dünnes zweiseitiges Klebeband.

Danach erfolgte die Ausrichtung der beiden Spiegel mit Hilfe der Sonne. Beobachtete ich diese durch das Interferometer, so sah ich mehrfach die Sonne entlang einer Linie. Ich versuchte nun durch Lösen bzw. Festziehen der 3 Justierschrauben diese Mehrfachbilder zur Deckung bringen. Danach konnte ich davon ausgehen, dass die Spiegel zumindest annähernd parallel sind.

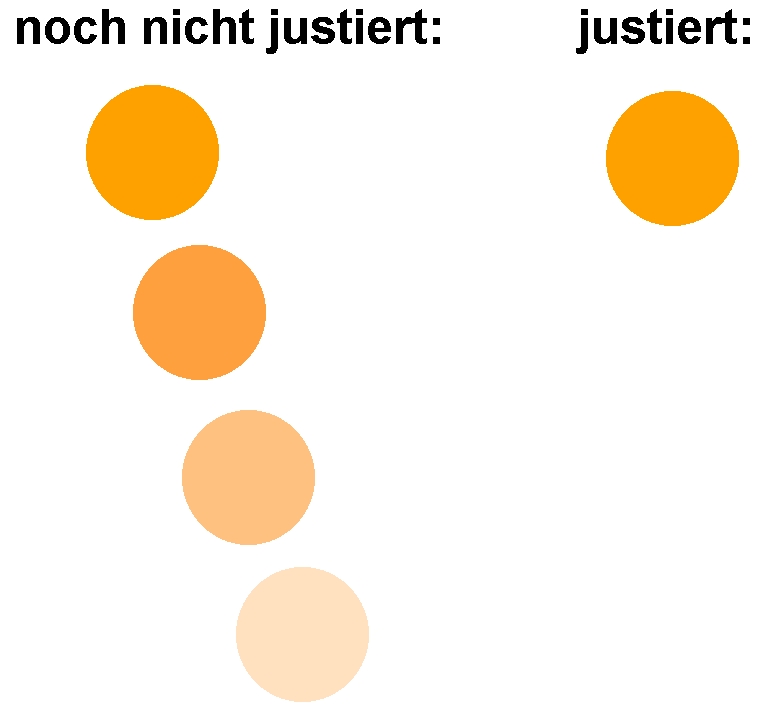
Um das Interferometer zu testen, benötigte ich noch einen Laser, eine milchig-weiße transparente Kunststoffplatte und eine Linse zur Kollimation. Der prinzipielle Aufbau sieht wiefolgt aus:
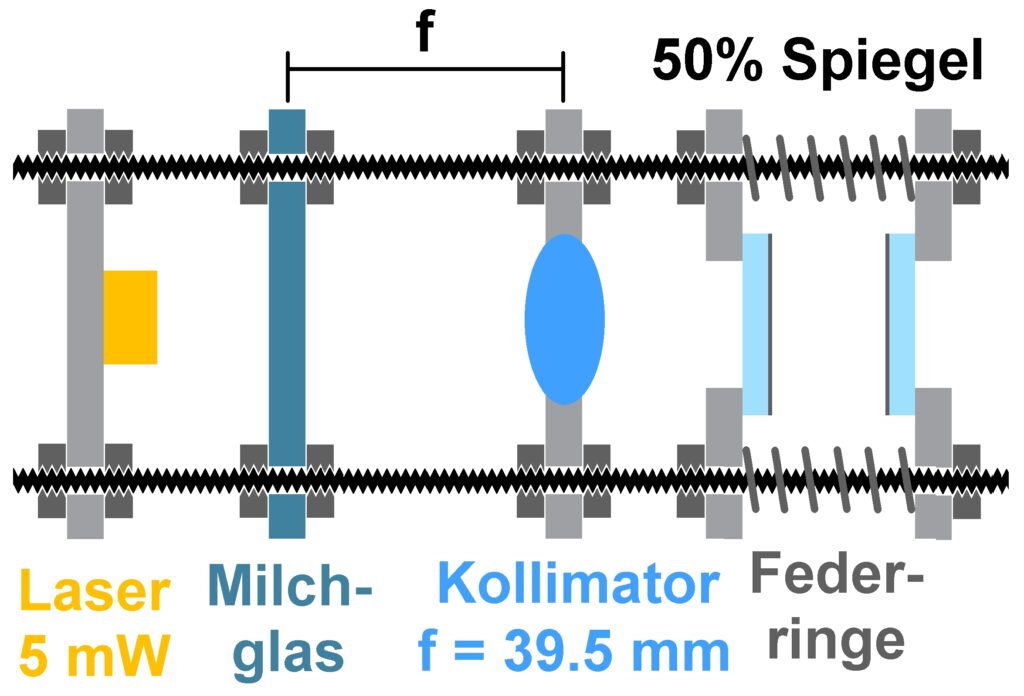
Getestet habe ich dies aber vor lauter Ungeduld auf dem Wohnzimmertisch im fliegenden Aufbau 😉


Und hier die ersten Ergebnisse:


Als ich die Interferenzringe sah, fühlte ich mich wie Robert Millikan bei der Entdeckung der Elementarladung. Hätte nicht gedacht, dass ich mit diesem Aufbau (so schnell) Erfolg habe. Jetzt geht es, den Aufbau wie oben skizziert umzusetzen. Montiert wird dann alles auf einer 20×9 cm Lochplatte.
Im zweiten Versuch mit dem Fabry-Perot-Interferometer möchte ich ja mittels Piezosummer versuchen, die Länge L des Zwischenraums zu verändern und am Ausgang mittels Photodiode die konstruktiven Interferenzen zu erfassen. Anders als beim obigen Versuch mit den Interferenzringen möchte ich hier auf die Oberflächenspiegel mit einem Reflexionsgrad von schätzungsweise 95% zurückgreifen. Dadurch würden die Interferenzmaxima deutlich schärfer werden als mit einem teildurchlässigen Spiegel.
Problem ist dann nur die sehr geringe Transmission. Um dies zu überprüfen, habe ich zunächst nur mit einem einzelnen Spiegel mit R = 0.95 das hindurchtretende Licht erfasst. Zum Einsatz kam hier mein Transimpedanzverstärker mit der Photodiode SFH203.
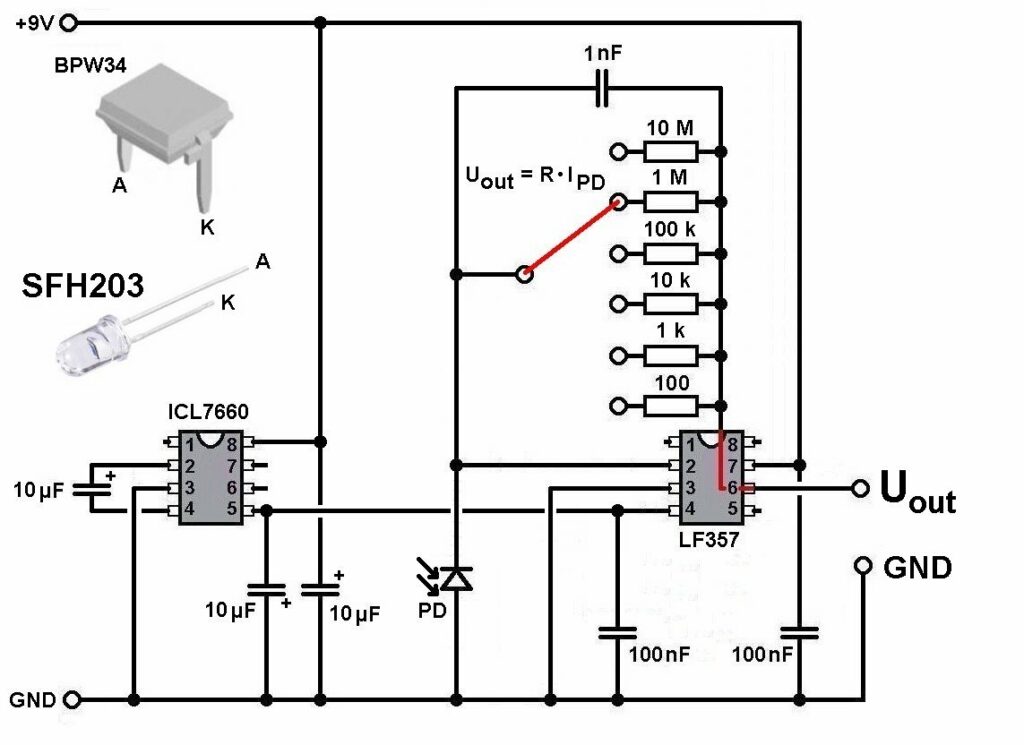

Hier der Testaufbau und die Ergebnisse im dunklen Zimmer (Anm.: Die Photos erscheinen nur durch die lange Belichtungszeit relativ hell) mit dem starken 200mW Laser:




Um bei Verwendung des Spiegels noch brauchbare Messwerte zu erhalten, musste ich die Verstärkung von 100 auf 10000 steigern. Bei einer vorausgesetzten Linearität wäre also die Intensität mit Spiegel um das 3000/(77/100) = ca. 3900-fache geringer als ohne. Dies kann bei einem Reflexionsgrad von geschätzten 95% (= 5% Transmission) natürlich nicht stimmen. Warum dies so ist, kann ich nicht wirklich sagen. Fakt ist aber, dass die hindurchgehenden Intensitäten sehr gering sind und dies, obwohl ich für obigen Versuch den starken Laser mit rund 200 mW verwendet habe.
Ich bin schon gespannt, ob ich dann bei Verwendung zweier Spiegel überhaupt noch visuell etwas erfassen und dadurch justieren kann. Mal schauen…
So, ich habe mich entschieden, das Interferometer vom restlichen Aufbau zu trennen. Dies hat den einfachen Grund, dass ich bei nicht korrekt eingestelltem Interferometer den ganzen Aufbau nicht immer wieder zerlegen muss. So stelle ich das Interferometer separat ein und kann es gegebenenfalls ohne größere Mühe nachjustieren. Der Aufbau sieht dann so aus:






Meine Söhne besorgen mir heute die Lochplatten beim Baumarkt, dann kann es weitergehen…
Der Aufbau beider Interferometer ist soweit fertig. Die Lochplatten haben die Abmessungen 300 x 100 mm bzw. 200 x 80 mm. Ich habe auch schon versucht, die beiden hochreflektiven Oberflächenspiegel des Interferometers mittels der Sonne auszurichten. Dies erwies sich aber als sehr schwierig, da das/die Sonnenbild/er nur extrem schwach zu sehen war/en. Wenn es mit der Sonne nicht funktionieren sollte, versuche ich es direkt mit dem 200mW-Laser. Welche Spannung der Piezo für Bewegungen im Bereich der Lichtwellenlänge benötigt, weiß ich auch noch nicht. Ich werde es einmal im mV-Bereich probieren und hoffen, mit dem Lichtdetektor dann schmale Maxima feststellen zu können.





Beim Interferometer für die Darstellung der Beugungsringe kommt ein 6×30 Sucher eines ausrangierten Newtonteleskops zum Einsatz.



Ich habe den ersten Aufbau für die Interferenzringe nochmals überprüft, indem ich mit dem Finger eine Kraft auf das Interferomter ausgeübt habe. Überraschenderweise haben sich die Interferenzringe nicht verändert. Dies widersprach meinen Erfahrungen, da ja schon Verschiebungen im Nanometerbereich eine Änderung des Musters hervorrufen müssten. Aus diesem Grund untersuchte ich das Bild der Interferenzringe genauer. Wenn man genau hinsieht bemerkt man zwei sich überlagernde Muster aus konzentrischen Kreisen. Eines mit größerem Ringabstand und eines mit näher beisammen befindlichen Ringen.

Die Länge L der interferenzverursachenden Schicht bedingt ja die Nähe der Interferenzringe. Für den Wegunterschied Δs gilt ja: Δs = 2·L·cos(α). Wenn L wächst, benötige ich für eine bestimmte Änderung von Δs nur einen kleineren Winkel α! Eine größere Länge L bewirkt also enger beisammenliegende Interferenzringe.
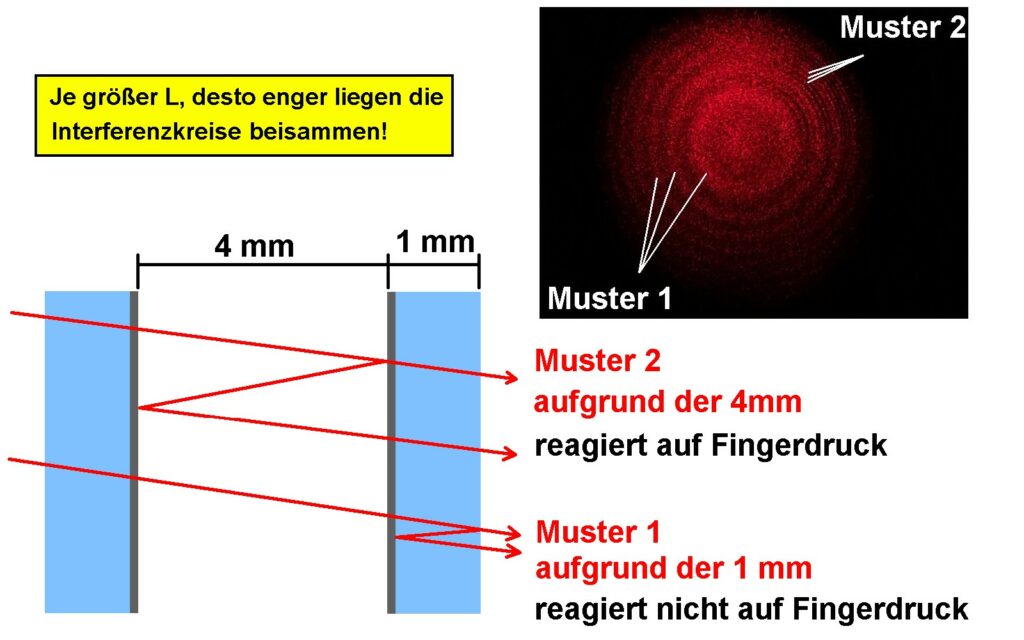
Deshalb vermute ich nun, dass die weiter auseinander liegenden Ringe (= Muster 1) durch Interferenz innerhalb eines Spiegelträgers zustande kommen. Die halbdurchlässigen Spiegel besitzen eine Dicke von rund 1 mm. Der Spiegelabstand L beträgt rund 4 mm. Daher müssten die Interferenzringe bedingt durch die Dicke des Glasträgers einen größeren Abstand voneinander haben als die gewünschte Interferenz durch den Spiegelabstand L. Dies würde auch begründen, warum das größere Interferenzmuster nicht auf den Fingerdruck reagiert. Denn durch diesen verändere ich eigentlich nicht wirklich den Glasträger an sich, nur den Abstand L zwischen den beiden Spiegeln.

Ich habe deshalb das gesamte Interferometer nochmals genauestens justiert. Diesmal habe ich aber nicht die Sonne dafür herangezogen, sondern den 5mW Laser. Fokusiere ich diesen auf die Milchglasplatte, so erkenne ich im Interferometerbild einzelne schwache Lichtreflexe, die sich wie bei der Sonne entlang einer Reihe anordnen. Durch die Justage brachte ich diese Mehrfachreflexe wieder genauestens in Deckung. Dadurch wurde das enger beisammen liegende Interferenzmuster (= Muster 2) besser sichtbar. Dieses reagiert nun wie erwartet auf leichten Fingerdruck. Auf dem oberen Bild schaut nun das “feinere” Interferenzmuster fast so aus wie das “gröbere” von den ersten Messungen. Dies ist aber dadurch begründet, dass ich das feinere Interferenzmuster durch das Fernrohr mit 6-facher Vergrößerung aufgenommen habe und dieses daher viel größer als mit dem Auge betrachtet wirkt.
Der fertige Aufbau von Interferometer-1:

Das zweite Interferometer mit dem Piezo und den hochreflektierenden Spiegeln werde ich nun ebenfalls nicht mit der Sonne, sondern mit dem Laser (in diesem Fall mit dem 200 mW Laser) justieren.
Gestern habe ich mich sehr lange mit dem zweiten Interferometer gespielt, welches ja die Spiegel mit R = 0.95 und den Piezosummer verwendet. Ich hatte gehofft, dass ich durch den hohen Reflexionsgrad eine deutlich bessere Finesse erhalte und ich am Ausgang eigentlich nur Dunkelheit und bei erfüllter konstruktiver Interferenz eben eine Transmission erhalte. Leider war dem nicht so. Ich habe wirklich einiges probiert: Laserstrahl mit minimaler bzw. größerer Divergenz, Blenden mit verschiedenen Durchmesser am Eingang des Interferometers usw.



Die Justage des Interferometers konnte durch die Mehrfachreflexe des Laserstrahls eigentlich ohne größere Schwierigkeiten erfolgen. Nur ich erhielt eben auch nach mehreren Justageversuchen nicht oben erwähntes Wunschresultat. Indes beobachtete ich Interferenzringe wie beim ersten Interferometer, deren Abstände und Zentrum durch die Justage des Interferometers nicht zu ändern waren. Sie waren auch in keinster Weise schärfer, was eigentlich durch den deutlich höheren Reflexionsgrad der Spiegel zu erwarten wäre.

Nur Dunkelheit und bei Ansteuerung des Piezosummers in regelmäßigen Abständen Transmission des Laserstrahls konnte ich also in keinster Weise erzielen. Den Versuch, diese scharfen Transmissionsmaxima mit der Photodiode zu erfassen, musste ich daher auch ad acta legen. Was ich aber mittels der sich bewegenden Interferenzringe bestimmen konnte, war der sinnvolle Ansteuerbereich des Piezosummers. Ungefähr 1 V war notwendig, um die Interferenzringe um einen Schritt weiterwandern zu lassen, was ja einer Verschiebung der Spiegel um eine halbe Wellenlänge entspricht. Demnach beträgt die Verschiebung des Piezos rund 650 nm : 2 = 325 nm pro Volt. Mittels Analyse eines Videos konnte ich den Wert auf 375 nm/V festlegen.

Aufgrund der ernüchternden Ergebnisse werde ich also das zweite Interferometer ebenfalls mit halbdurchlässigen Spiegeln ausstatten. Denn die damit erzielten Interferenzringe waren beim Interferometer 1 sehr deutlich zu sehen und auch ihre Bewegung bei Ausübung von Druck auf das Interferometer war schön zu beobachten. Ich werde dann einfach mittels Handyteleobjektiv (8-fache Vergrößerung) die Wanderung der Interferenzringe in Abhängigkeit von der Piezospannung erfassen.
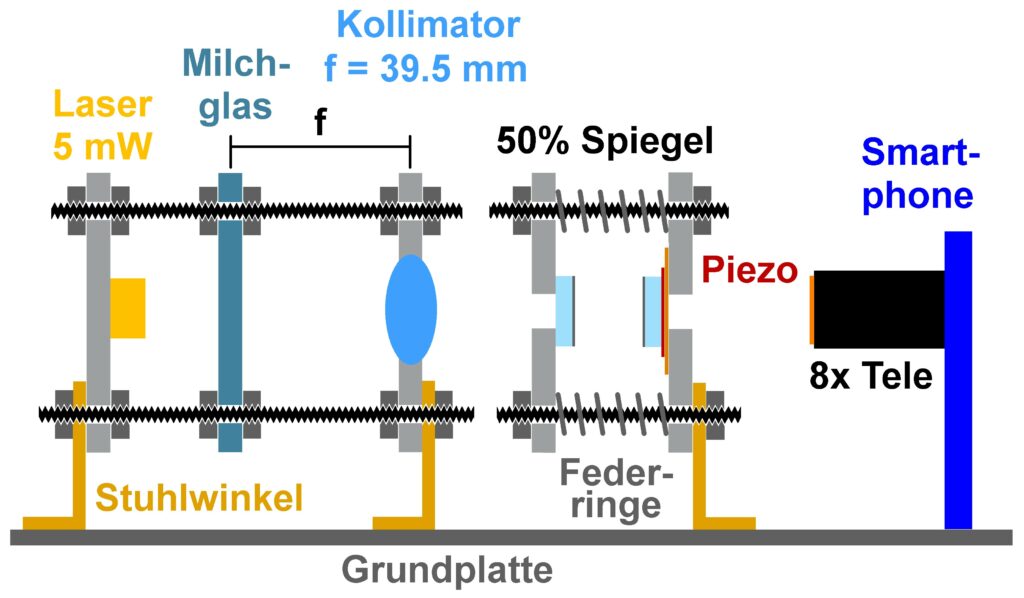
Die “Elektronik” für das zweite Interferometer ist auch fertig. Das rote 5V-Lasermodul kann mit einer Spannung von 1.25 bis 5V geregelt werden und der Piezo wird mit einer Spannung zwischen 0 und 9V gespeist.



Die Einzelteile des zweiten Interferometers sind fertig und warten auf den Zusammenbau. Für das Handy + Teleaufsatz hatte ich noch eine günstige Halterung im Fundus.

Die Nummer 2 ist auch fertig aufgebaut. Ich werde aber vermutlich noch einen step-up-Wandler zwischen Batterie und Schaltung verwenden, damit der Verstellbereich des Piezo größer wird. Jetzt warte ich eigentlich nur mehr auf das Handyteleobjektiv. Die Justage des zweiten Interferometers gestaltete sich ein wenig schwieriger als beim Ersten. Ich musste für schöne Interferenzringe die drei Justierschrauben unterschiedlich stark festziehen. Daher verwendete ich bei einer Schraube innen noch eine nur 0.5 mm dicke M4-Beilagscheibe. Jetzt sind alle 3 Justierschrauben in etwa gleich stark festgezogen.
Eine Bemerkung noch zur Einstellung des Interferometers: Das grobe Interferenzmuster (siehe Muster 1 weiter oben) erscheint eigentlich sofort. Aber dieses Muster ist eben nicht das Gewünschte, da es nicht durch den Zwischenraum des Interferometers zustande kommt und somit auch nicht auf Fingerdruck reagiert. Erst wenn man die Lichtreflexe (siehe auch weiter oben) ganz genau zur Deckung gebracht hat, erscheint mit etwas Glück das feinere Muster 2. Hierzu sind aber doch ein wenig Geschick und Geduld notwendig. Mit etwas Übung schafft man dies aber innerhalb von 5 Minuten. Dieses Muster 2 reagiert dann wie gewünscht auf geringsten Druck auf die Interferometeraluplatten.

So, letztes Kapitel zu meinen Fabry-Perot-Interferometern: Heute ist das 8x Teleobjektiv fürs Smartphone angekommen. Die Vergrößerung (es gibt noch Varianten mit 12-fach bzw. 20-fach) passt eigentlich recht gut und die Wanderung der Interferenzringe bei variierender Piezospannung ist schön zu sehen. Etwas problematisch ist nur die Handyhalterung, denn diese klemmt das Handy seitlich genau am Ort der Ein/Aus-Taste und fährt dieses dann immer wieder runter. Abhilfe schaffte ein kurzerhand angeklebter Distanzhalter.








