Die Newtonschen Ringe sind ein einfacher Versuch zum Thema Interferenz. Sie bestehen aus zwei Glaselementen und zwar einer ebenen Glasplatte und einer plankonvexen Linse mit sehr großem Krümmungsradius R.

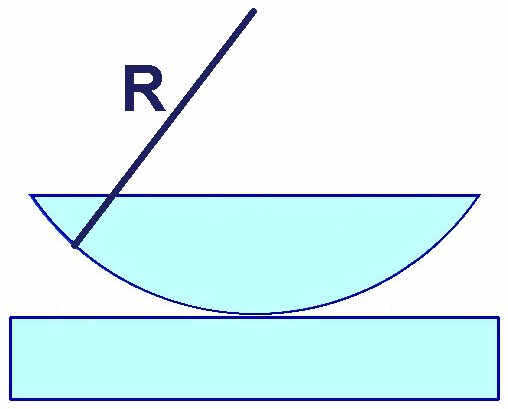
Wie kommt es aber nun zu Interferenzerscheinungen? Bestrahlt man den Apparat mit Licht, so trifft dieses auf seinem Weg auf den Luftzwischenraum der beiden Gläser. An den Grenzschichten kommt es zu Transmission bzw. Reflexion. Die unterschiedlichen Lichtstrahlen besitzen einen unterschiedlichen Weg und besitzen daher bei der Wiedervereinigung einen bestimmten Gangunterschied. Beträgt dieser Gangunterschied ein Vielfaches der Wellenlänge, also n·λ, so kommt es zur konstruktiven Interferenz (Verstärkung). Beträgt dieser Gangunterschied allerdings ein ungeradzahliges Vielfaches der halben Wellenlänge, also (2·n + 1)·λ/2, so löschen sich die Lichtwellen aus und es kommt zur destruktiven Interferenz.

Ganz entscheidend für diesen Gangunterschied ist der jeweilige Abstand d zwischen den beiden Gläsern. Für diesen gilt:

In Durchsicht ergibt sich also folgendes Muster (heller Ring im Zentrum): 

In der Draufsicht ist es genau anders herum und das Muster startet im Zentrum mit einem dunklen Ring (destruktive Interferenz):

Auf aliexpress bin ich über ein sehr günstiges Angebot gestolpert. Da man aus Österreich aber seit 2023 weitestgehend nichts mehr auf aliexpress bestellen kann, hat mir ein sehr netter Herr aus der Schweiz die Newtonschen Ringe bestellt und dann weiter zu mir versandt. Vielen lieben Dank nochmals dafür 😉

Trägt man nun die Radien r²(n) etwa der dunklen Ringe in Draufsicht in Abhängigkeit vom Zählindex n auf, so müsste man eine ansteigende Gerade durch den Ursprung erhalten mit der Steigung k = λ · R. Daraus lässt sich dann bei bekannter Wellenlänge λ der Krümmungsradius R bestimmen. Zur Beleuchtung sollte eigentlich ein roter Diodenlaser dienen. Ich hatte aber mit diesem Probleme, ein schön starkes Interferenzmuster zu erhalten.

Daher habe ich das im Sonnenlicht sichtbare Interferenzmuster ausgewertet. Hier erhält man dann im Gegensatz zur monochromatischen Beleuchtung kein scharfes Hell-Dunkel-Muster, sondern mehr oder weniger färbige Ringe. Aber ich konnte trotzdem zumindest einigermaßen Radien bestimmen:

Das Ergebnis für den Krümmungsradius R lautet:

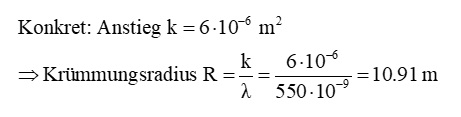
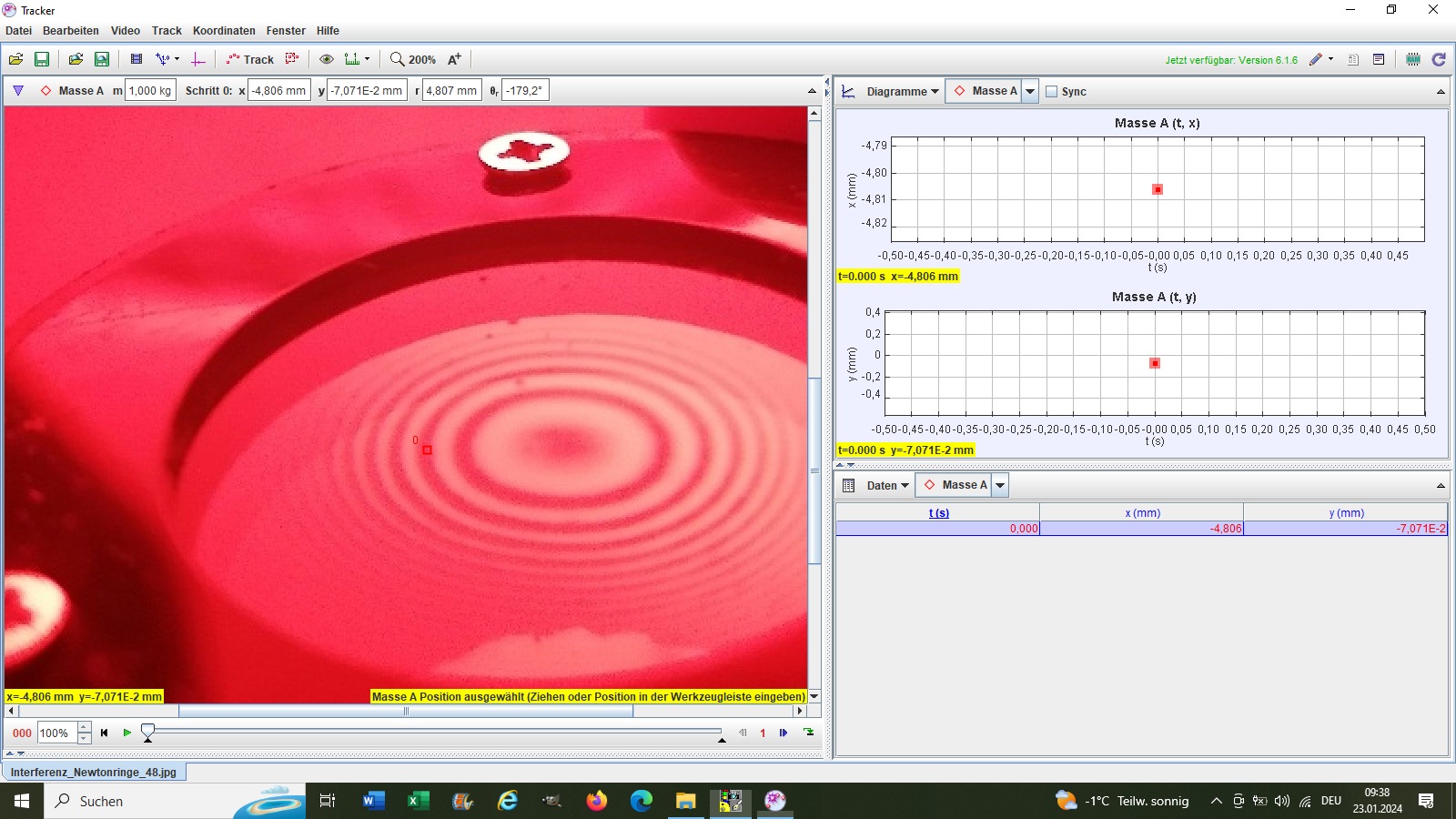
Die färbigen Ringe haben mich nicht wirklich zufrieden gestellt. Da die Beleuchtung mit einem Laser nicht funktionierte, musste ich eine andere Lösung finden. Zum Glück kam mir die Idee, die Ringe einfach durch einen Farbfilter zu betrachten. In meinem Fundus befanden sich noch solche Filter, welche ich vor einiger Zeit einmal geschenkt bekam. Nun kamen sie zum Einsatz…

Damit waren die Ringe nicht nur schärfer, ich konnte auch mehr von diesen für die Messung erfassen:

Die Quadrate der Radien r² wurden dann gegen die Zählvariable n aufgetragen und ich erhielt eine schöne Gerade:

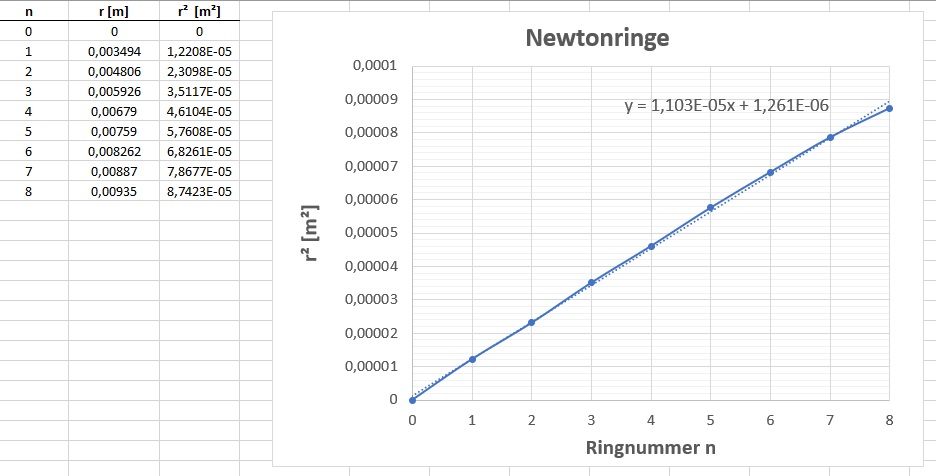
Aus dem Anstieg der Geraden konnte ich den Krümmungsradius R berechnen:

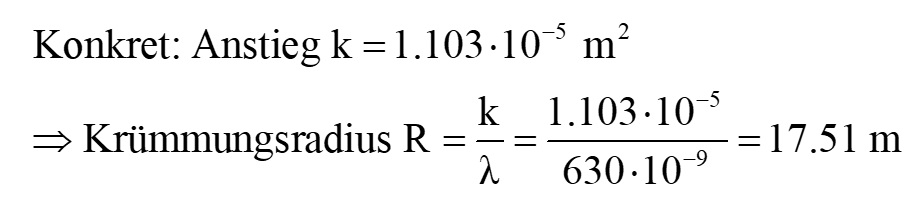
Hier noch das Youtube-Video: