Dieser berühmte, nach den beiden Physikern James Franck (1882–1964) und Gustav Hertz (1887–1975) benannte Versuch, bewies erstmalig experimentell die Existenz von diskreten Quantenzuständen im Atom.
Der prinzipielle Aufbau ist simpel. Eine Elektronenröhre mit Gitter wird zwischen Kathode und Gitter mit einer variablen Gleichspannung (0–40V) versorgt. Zwischen Gitter und Anode liegt eine kleine Gegenspannung (0–5V).
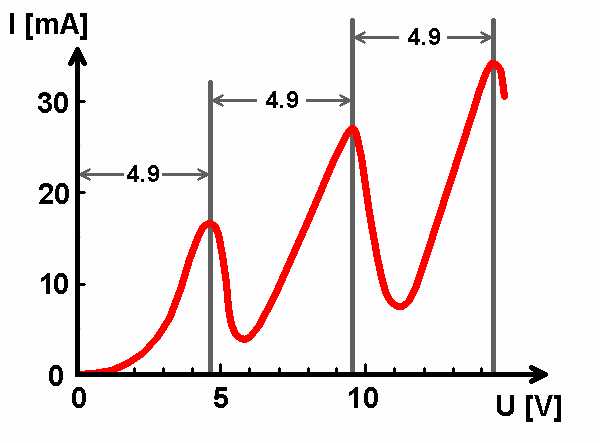
Erhöht man nun die Gitterspannung, so würde man erwarten, dass die beschleunigten Elektronen die geringe Gegenspannung überwinden können und damit der Anodenstrom ab einer gewissen Schwelle kontinuierlich ansteigt. Es sind aber indes regelmäßige Einbrüche des Anodenstroms zu beobachten. Wie kommt es zu diesen?
Die Energiezustände im Atom sind diskret, d.h. es kommen nicht alle Energien innerhalb bestimmter Grenzen vor, sondern nur ganz spezielle. Dies kann man etwa mit einem Sprungturm im Schwimmbad vergleichen. Auch hier kommen nicht sämtliche potentiellen Energien vor, sondern nur ganz bestimmte z.B. für h = 1 m, 3 m, 5 m, 7.5 m und 10 m.

Bildquelle: https://www.myheimat.de/donauwoerth/freizeit
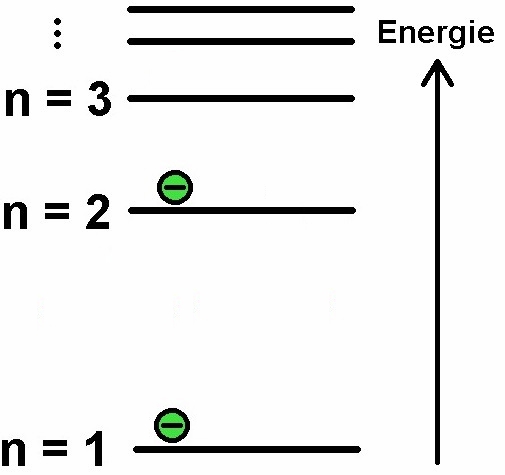
Ähnlich ist es wie gesagt auch im Atom. Um ein Elektron von einem niedrigeren Energieniveau in ein höheres zu „heben“, bedarf es einer ganz bestimmten Energie in Form von Licht oder etwa in Form von Stößen. Besitzen die beschleunigten Elektronen genau diese Anregungsenergie, so können sie diese Energie auf die Gasatome in der Elektronenröhre (zumeist wird Quecksilber oder Neon als Füllgas verwendet) übertragen, anderenfalls nicht. Nach diesem Stoß besitzen die bewegten Elektronen natürlich eine um diese Anregungsenergie reduzierte kinetische Energie. Dies hat zur Folge, dass die durch Stöße nun langsameren Elektronen die Gegenspannung nicht mehr überwinden können und daher der Anodenstrom sinkt.
Quecksilber besitzt zum Beispiel eine Anregungsenergie von 4.9 eV. Werden die Elektronen mit einer Spannung U < 4.9V beschleunigt, reicht ihre Energie zur Anregung des Quecksilbergases nicht aus und die Elektronen erreichen trotz der Gegenspannung die Anode. Beträgt nun die Beschleunigungsspannung aber 4.9V, so reicht die kinetische Energie der Elektronen für eine Anregung der Quecksilberatome aus. Demnach verlieren die stoßenden Elektronen diese Energie von 4.9 eV. Auf diese Weise stark abgebremst oder sogar zum Stillstand gebracht, können sie die Gegenspannung nicht mehr überwinden.
Steigert man nun die Beschleunigungsspannung weiter, so nehmen die ein Mal bereits abgebremsten Elektronen wieder so viel Fahrt auf, dass sie die Gegenspannung abermals überwinden können. Nach einem Minimum bei 4.9V steigt also der Anodenstrom für größere Gitterspannungen wieder an. Aber nur solange, bis die Elektronen ein zweites Mal eine kinetische Energie von 4.9 eV erreichen. Dies ist bei einer Beschleunigungsspannung von 2 · 4.9 = 9.8V der Fall. Auch in diesem Bereich sinkt der Anodenstrom zum zweiten Mal. Eine Erhöhung von U bewirkt danach wieder einen Anstieg des Anodenstroms, bis dieser bei U = 3 · 4.9 V neuerlich sinkt.
Auf diese Weise besitzt der Verlauf des Anodenstroms in Abhängigkeit von der Beschleunigungsspannung regelmäßige, im Abstand von 4.9V befindliche Minima.
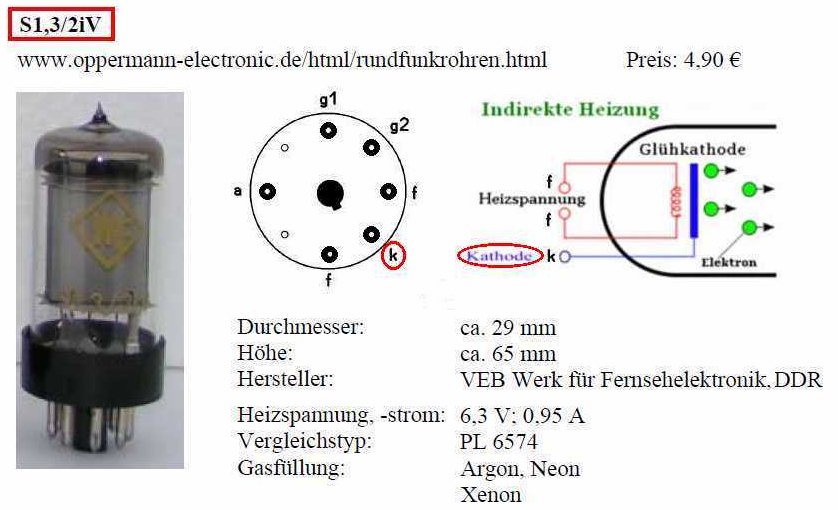
Sogenannte Franck-Hertz-Röhren sind sehr teuer (im Bereich von 400-500 Euro). Man kann den Versuch aber weitaus günstiger umsetzen, indem man auf ein Thyratron des Typs 1,3/2iV zurückgreift. Dieses wird etwa auf ebay für einen geringen Betrag angeboten. Dieses Thyratron besitzt eine Füllung mit Argon, Neon bzw. Xenon.
Die damit erhaltenen regelmäßigen Minima im Anodenstrom sind zwar nicht so schön ausgeprägt wie bei Verwendung einer Quecksilber- oder Neon-Franck-Hertz-Röhre, aber der sehr geringe Preis tröstet über dieses Manko hinweg.
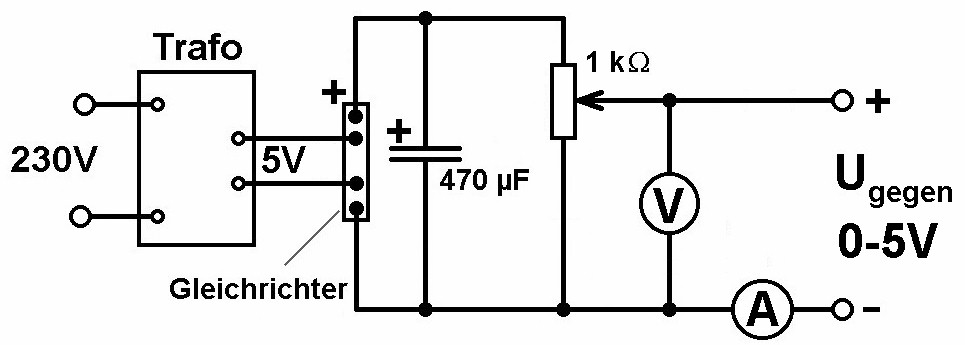
Benötigt wird für den Versuch neben der Röhre eine variable Spannungsversorgung für die Heizung (6.3V/1A), eine variable Beschleunigungsspannung (0–40V) und eine variable Gegenspannung (0–5V). Zudem wird für den geringen Anodenstrom im µA-Bereich ein hoch auflösendes Amperemeter benötigt. Viele Multimeter können aber bereits Ströme mit einer Auflösung von 0.1 µA auflösen, was für diesen Versuch eigentlich ausreicht.











Variante 2
In einem englischsprachigen Buch „experimental physics for students“ von R.M. Whittle und J. Yarwood bin ich auf eine weitere einfache Variante des Franck-Hertz-Versuchs gestoßen.

Hier der sehr einfache Schaltplan mit einer 2D21-Röhre als Herzstück:
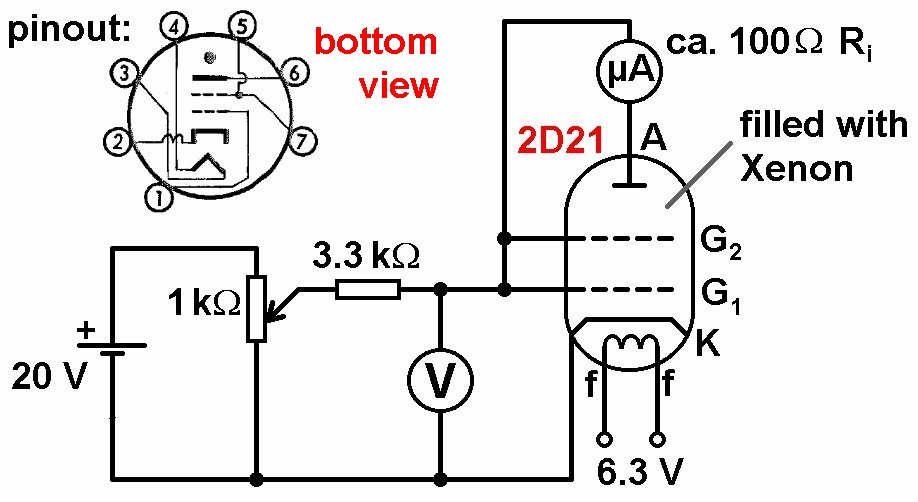
Diese Röhre ist mit Xenon gefüllt. Genau dessen Anregung durch Elektronen wird in diesem Experiment untersucht bzw. nachgewiesen. Den Heiztrafo (6V) und die Röhren habe ich wie so oft über die österreichische Verkaufsplattform http://www.willhaben.at gebraucht erstanden:





Den dazu passenden Röhrensockel habe ich bei mir in Graz in einem Elektronikgeschäft besorgt:

Für die Anoden- und Gitterspannung verwende ich ein kleines 24V-Netzteil. Dieses hatte ich noch zuhause liegen…


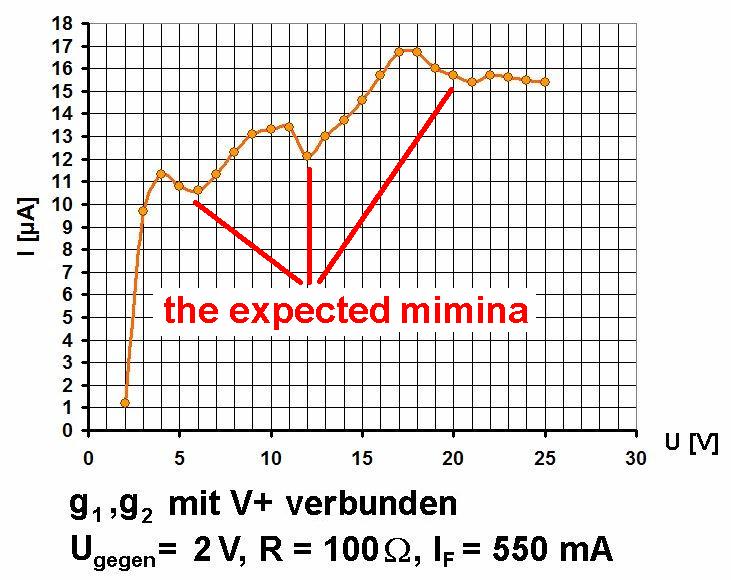
Im Gegensatz zum Originalschaltplan verwende ich anstelle des 10 kΩ-Vorwiderstands einen mit nur 3.3 kΩ. Mit dem 10 kΩ-Widerstand brach die Gitter- und Anodenspannung viel zu stark ein und betrug selbst bei voll aufgedrehtem Potentiometer nur rund 3 V. Mit dem geringeren Vorwiderstand komme ich nun auf ca. 8-9 V, was für die I(U)-Kennlinie ausreicht.

Der Trick der Schaltung ist folgender: Die von der indirekt geheizten Kathode emittierten Elektronen gelangen zu den positiv vorgespannten Gittern. Durch den Anodenstrom fällt am Amperemeter eine kleine Spannung ab. Dies führt dazu, dass das Anodenpotential leicht unterhalb der beiden Gitter liegt. Werden nun die Xenonatome durch die Elektronen angeregt, sodass diese Energie verlieren, so gelangen diese nicht mehr zur gegenüber den Gittern leicht negativ vorgespannten Anode und der Anodenstrom sinkt. In der I(U)-Kennlinie müsste man also bei einer bestimmten Spannung einen Rückgang des Anodenstroms beobachten können.
Gestern konnte ich den Aufbau vollenden…




…und eine Messung durchführen:
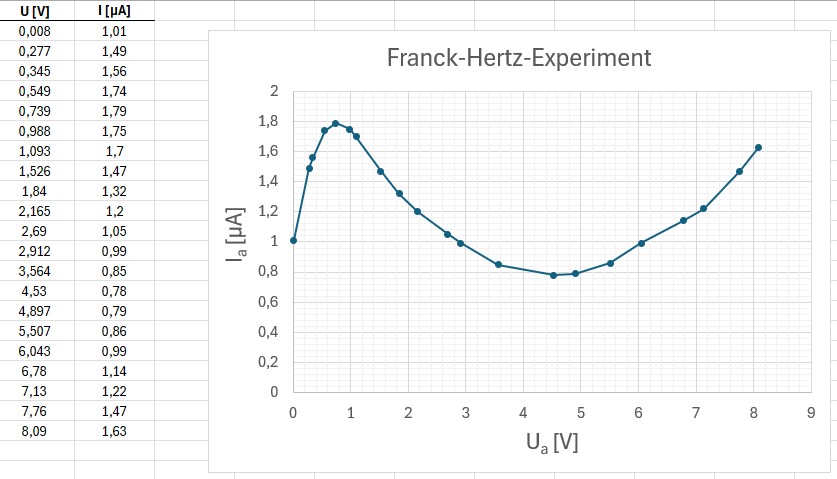
Wie man gut erkennen kann nimmt zunächst der Anodenstrom mit steigender Gitter-/Anodenspannung zu, um dann durch inelastische Stöße der Elektronen mit den Xenon-Atomen abzufallen. Erst bei höherer Anodenspannung steigt der Strom wieder an…

