Das Elastizitätsmodul E eines Festkörpers beschreibt quasi dessen Steifigkeit. Ein Stoff mit hohem Elastizitätsmodul, z.B. Eisen, ist demnach steifer als ein Stoff mit geringem E, zum Beispiel Gummi.
Für eine Feder, welche gedehnt wird, gilt ja das Hooksche Gesetz F = k · x. Dehnt man eine Feder mit der Federkonstante k um die Länge x, so ist dafür die Kraft F = k · x notwendig. Die Federkonstante k entspricht demnach der notwendigen Kraft F, um die Feder um 1 m zu dehnen. Besitzt die Feder eine große Federkonstante k, so ist für deren Dehnung eine größere Kraft notwendig, die Feder ist härter. Bei geringem k ist es umgekehrt und die Feder ist weicher.
Möchte man nun anstelle einer Feder einen Festkörper dehnen, so ist die Situation ähnlich/vergleichbar. Hier kommt nun aber anstelle der Federkonstante k das Elastizitätsmodul E zum Tragen. Die Formel lautet: σ = F/A = E · ε = E · ΔL / L0.
σ ist die am Festkörper mit der Querschnittsfläche A wirkende mechanische Spannung (Schubspannung), also die Kraft F geteilt durch den Querschnitt A. ε ist die Dehnung des Festkörpers, also die relative Längenänderung ΔL / L0, wenn die Länge des ungedehnten Festkörpers L0 beträgt.
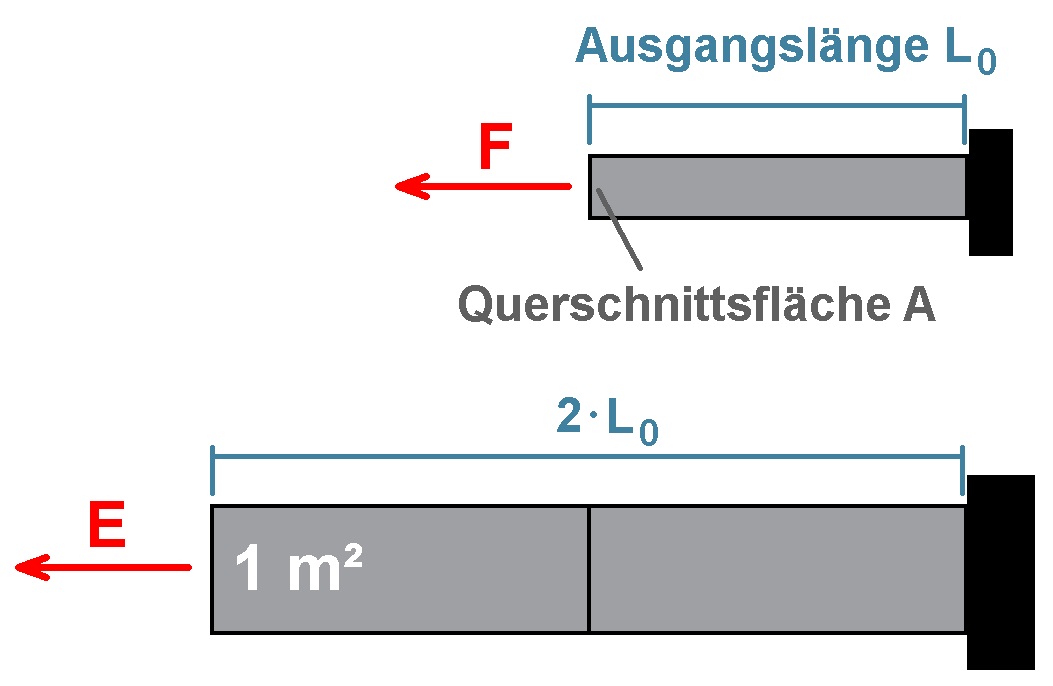
Wirkt also auf den Festkörper an dessen Ende eine Kraft F, so bewirkt dies eine Dehnung. Eine doppelte Kraft resultiert in einer doppelt so großen Dehnung. Die Proportionalitätskonstante zwischen der Spannung/Kraft und der Dehnung ist genau das Elastizitätsmodul E. Es entspricht also quasi der Federkonstante bei einer Feder.
Das Elastizitätsmodul E ist genau die notwendige Kraft F, um einen Festkörper mit der Querschnittsfläche A = 1 m² auf seine doppelte Ursprungslänge L0 zu dehnen. Dann wird nämlich die Dehnung ε = ΔL / L0 = (L – L0)/ L0 = (2·L0 – L0)/ L0 = L0/ L0 = 1. Daran erkennt man, dass das Elastizitätsmodul E eine für Festkörper in der Regel sehr große Zahl sein muss. Denn ein extrem dicker Stab aus zum Beispiel Eisen mit der Querschnittsfläche A = 1 m² lässt sich nur durch enormen Kraftaufwand auf seine doppelte Ursprungslänge dehnen. Für Stahl beträgt E etwa 180 · 10^ 9 N/m².
Variante 1: Drahtdehnung
Wie kann man nun experimentell dieses Elastizitätsmodul E bestimmen? Nun, die erste Möglichkeit besteht darin, die obige Definitionsformel für E praktisch umzusetzen, indem man einen Draht mit zunehmenden Gewichten belastet und die entsprechende Dehnung notiert. Trägt man die Spannung σ gegen die Dehnung ε auf, so entspricht dem Elastizitätsmodul E genau der Geradenanstieg k! 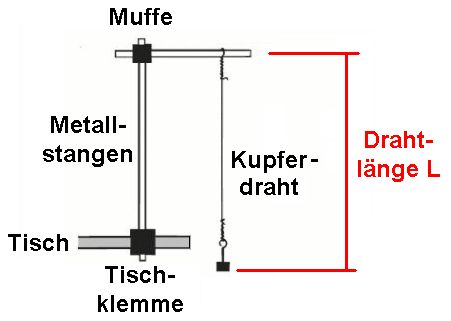
Wichtig bei diesem Versuch ist es, nur im elastischen Bereich zu bleiben, sprich den Draht nicht zu sehr zu dehnen. Denn bei zu starker Belastung/Dehnung kommt man in den plastischen Bereich und die Gerade flacht stark ab…
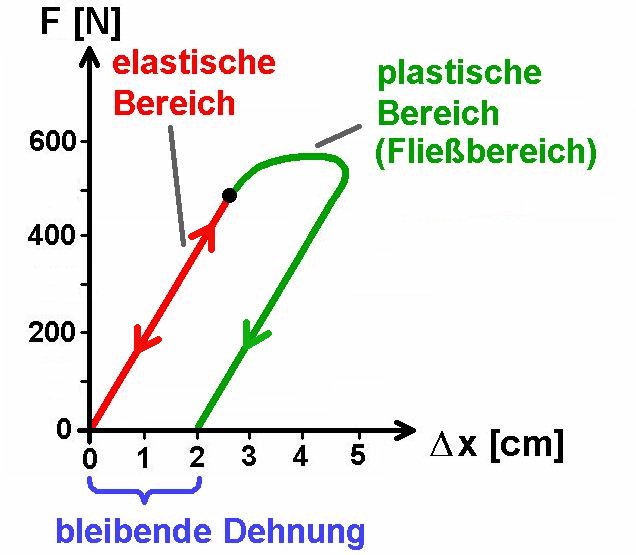
Bei zu starker Dehnung kommt auch noch hinzu, dass die Querschnittsfläche A deutlich abnimmt. Der Draht wird ja durch die Dehnung nicht nur länger, sondern auch dünner. Man müsste dann zur Berechnung der Spannung σ immer den aktuellen Querschnitt A berücksichtigen!
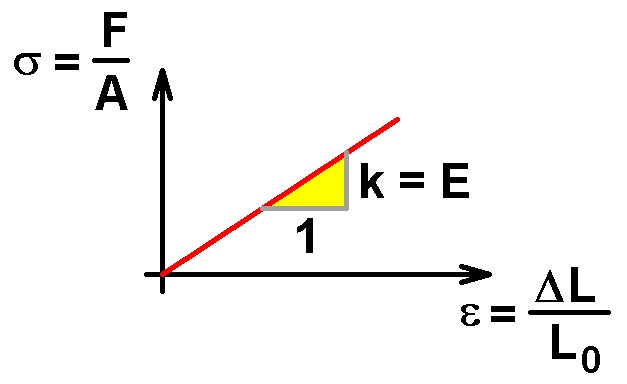
Als Draht habe ich mich für 0.2 mm dicken Kupferdraht entschieden. Diesen habe ich auf ebay.com erworben…

Die für die Dehnung des Drahts aufgebrachte Kraft bestimme ich mit der Kofferwaage. Zur Ermittlung der Dehnung habe ich einfach ein Klebeband an einer Stelle des Drahts angebracht und den Zollstock parallel zum Draht montiert:


Für eine Dehnung von ΔL = 3 mm war eine „Kraft“ von 1.255 kg notwendig, also 1.255 · 9.81 N. Damit lässt sich das Elastizitätsmodul einfach berechnen:

Variante 2: Biegung einer Metallleiste
Eine weitere Möglichkeit das Elastizitätsmodul E experimentell auf einfache Art zu bestimmen besteht darin die Biegung einer Metallleiste in Abhängigkeit von der angewandten Kraft zu dokumentieren. Spannt man eine Metallleiste auf einem Tisch fest und belastet man deren Ende zunehmend mit Gewichten, so biegt sich die Leiste logischerweise immer stärker. Aus dieser Biegung lässt sich das Elastizitätsmodul berechnen.
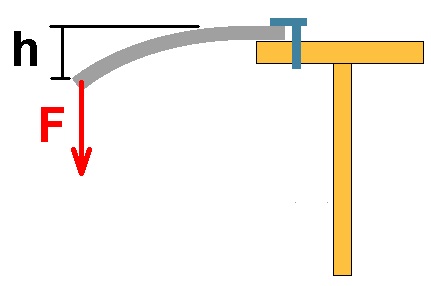
Trägt man nun die notwendige Kraft F für die Biegung h auf, so müsste man eine Gerade erhalten. Aus deren Anstieg k lässt sich E ermitteln, da k direkt proportional zu E ist. Eine Leiste mit doppelten Elastizitätsmodul benötigt also für eine Biegung h die doppelte Kraft F. Natürlich hängt die notwendige Kraft auch noch entscheidend von der Länge L der eingespannten Metallleiste ab. Je kürzer die zu biegende Metallleiste, desto größer wird die notwendige Kraft. Die Kraft F ist proportional zu 1/L³. Für eine halb so lange Leiste benötigt man also die 8-fache Kraft F, um sie um dasselbe h durchzubiegen!
Nun zur Herleitung der Formel:
Zunächst bestimmen wir den Biegeradius R in Abhängigkeit von L und h. Dabei nutzen wir die Näherungsformel für den Cosinus und zwar
cos(α) = 1 – (α² / 2) ; Winkel α in Bogenmaß = Kreisbogen b / Radius r
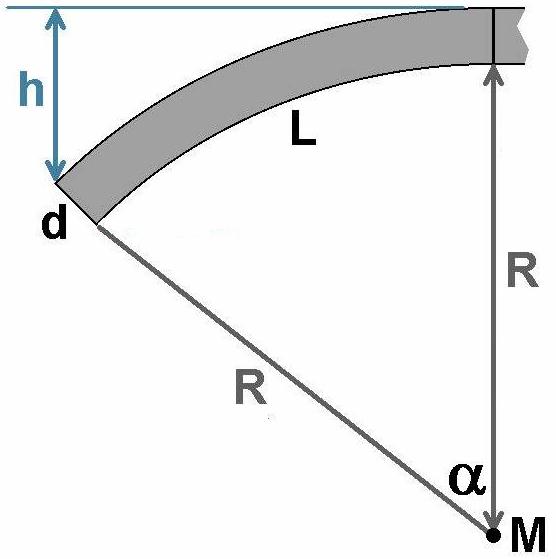
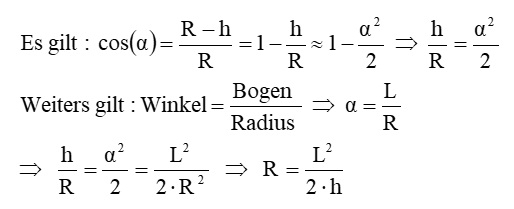
Gehen wir davon aus, dass sich die Leistenmitte (genau bei d/2) nicht dehnt, d.h. noch die Ausgangslänge L besitzt.

Nun bestimmen wir die Kraft dF(x) in Abhängigkeit vom Abstand x zur Leistenmitte (siehe Abbildung). Wir betrachten hierzu im Abstand x von der neutralen „Faser“ nur eine sehr dünne Leistenschicht der Breite b, der Höhe dx, und der gedehnten Länge L + ΔL!
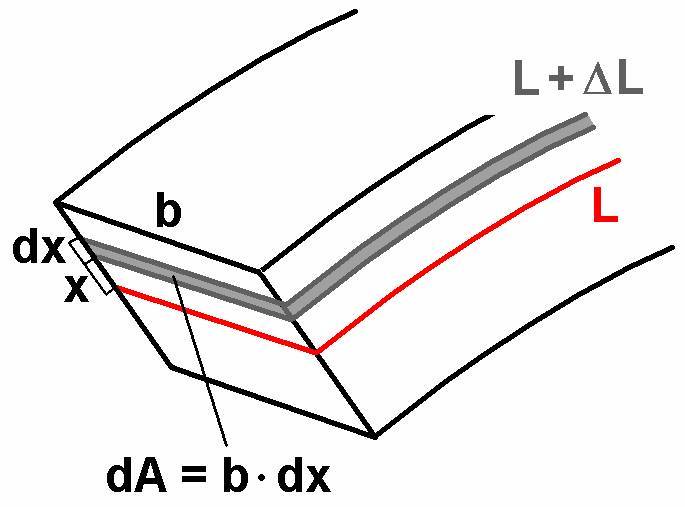
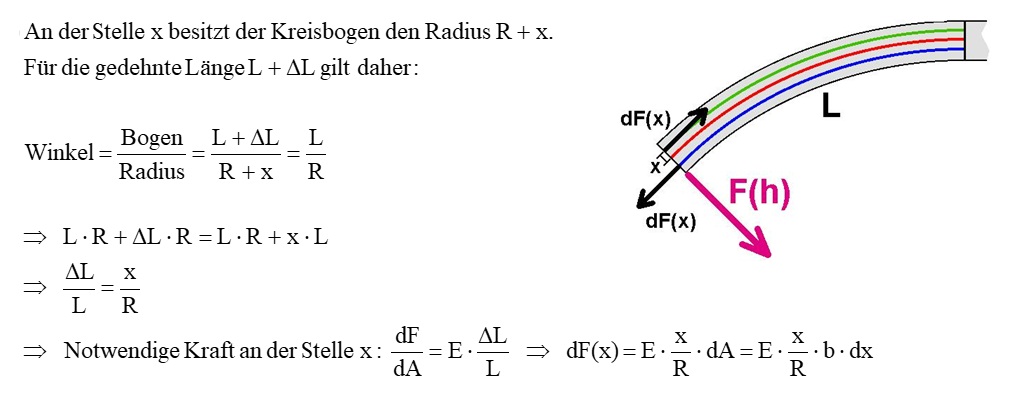
Mit dieser nun bekannten Kraft dF(x) in Abhängigkeit von x können wir das Drehmoment der verbogenen Leiste berechnen. Es gilt:
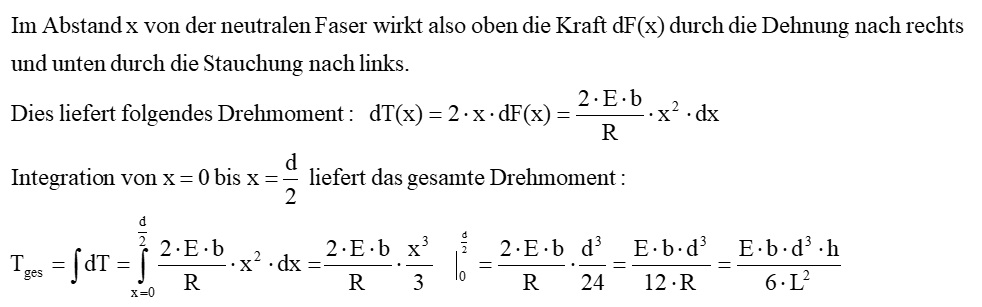 Dieses nach rechts wirkende Drehmoment T der Leiste muss genau dem zur Biegung aufgebrachten, nach links wirkenden Drehmoment T = F · L entsprechen. Daraus folgt:
Dieses nach rechts wirkende Drehmoment T der Leiste muss genau dem zur Biegung aufgebrachten, nach links wirkenden Drehmoment T = F · L entsprechen. Daraus folgt:
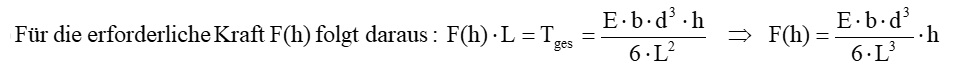
Es besteht also ein linearer Zusammenhang zwischen der zur Verbiegung der Leiste notwendigen Kraft F und der Durchbiegung h am Ende der Leiste.
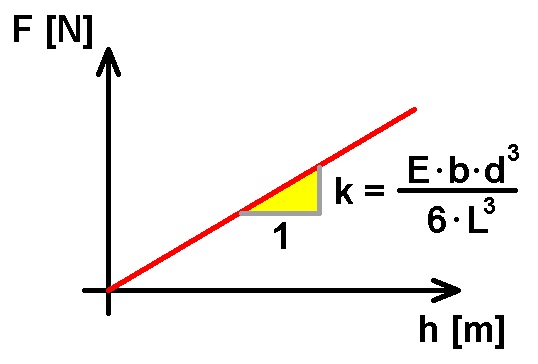
Im Anstieg k steckt unter anderem das Elastizitätsmodul E. Je größer E, desto steifer die Leiste und desto steiler der Graph F(h). Der Anstieg k ist zudem proportional zu 1/L³. Was bedeutet dies? Spanne ich eine nur halb so lange Metallleiste ein, so steigt die Kraft F auf das 8-fache an, wenn ich die nun kürzere Leiste um dasselbe h durchbiegen möchte! Eine kürzere Leiste ist also deutlich steifer…

Die Belastung der Leiste erfolgt wohl mit den Gewichten meiner Fernrohrmontierung.



Ein einzelnes Gewicht besitzt eine Masse von rund 3.14 kg, was ja einer Gewichtskraft F = m · g = m · 9.81 = 30.80 N entspricht. Insgesamt habe ich 3 Gegengewichte zur Verfügung.
Um bei der Belastung der Leisten flexibler zu sein, habe ich mir auf Amazon eine günstige Kofferwaage als Kraftmesser besorgt:

Bezüglich der Metallleisten schaue ich mich beim örtlichen Baumarkt um, wobei ich mich für eine aus Aluminium bzw. eine aus Stahl entschieden habe:
Die beiden Metallleisten bekam ich von meinem jüngeren Sohn zu Weihnachten geschenkt. Über Geschenke die ich wirklich gebrauchen kann freue ich mich riesig 🙂
Für die 4 mm dicke Stahlleiste habe ich zum Bestimmen der Kraft die Kofferwaage verwendet:





Hier die aufgebrachte Kraft F in Abhängigkeit von der Verbiegung h:
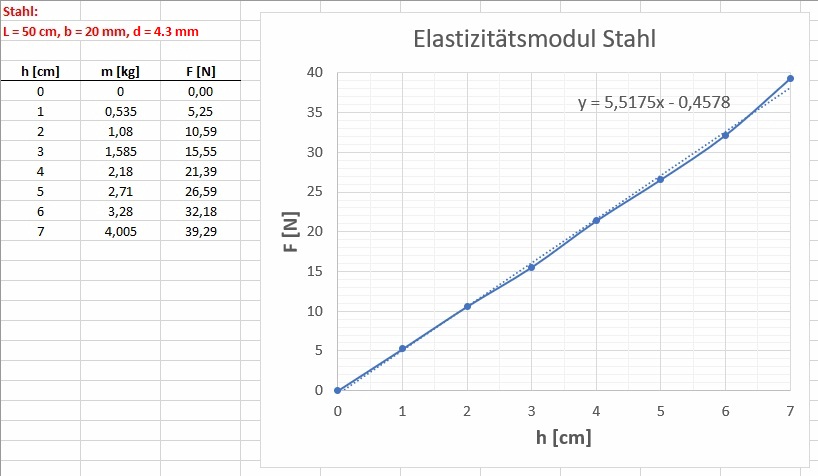
Der Anstieg beträgt k = 551.75 N/m. Diesen Wert benötige ich dann für die Bestimmung des Elastizitätsmoduls…
Die nur 2 mm dünne Aluminiumleiste war deutlich einfacher zu biegen. Daher verwendete ich nicht die Kofferwaage, sondern belastete die Leiste an deren Ende mit unterschiedlichen Gewichten.






Der experimentell ermittelte Kraftanstieg für die Aluleiste betrug nur 55.08 N/m:

Mit diesen beiden Anstiegen k konnte dann das Elastizitätsmodul E von Stahl bzw. Aluminium berechnen:

Die so erhaltenen Werte liegen relativ nahe an den Sollwerten, Heureka 😉
Variante 3: Schallgeschwindigkeit in Festkörpern
Eine letzte Möglichkeit zur einfachen Bestimmung des Elastizitätsmoduls E besteht darin, die Schallgeschwindigkeit in Festkörpern/Metallen zu bestimmen. Ich habe vor längerer Zeit eine Simulation zur Ermittlung der Geschwindigkeit von Wellen programmiert. Die Basis bilden Teilchen der Masse m, welche über Federn mit der Federkonstante k mit ihren Nachbarn flexibel verbunden sind.
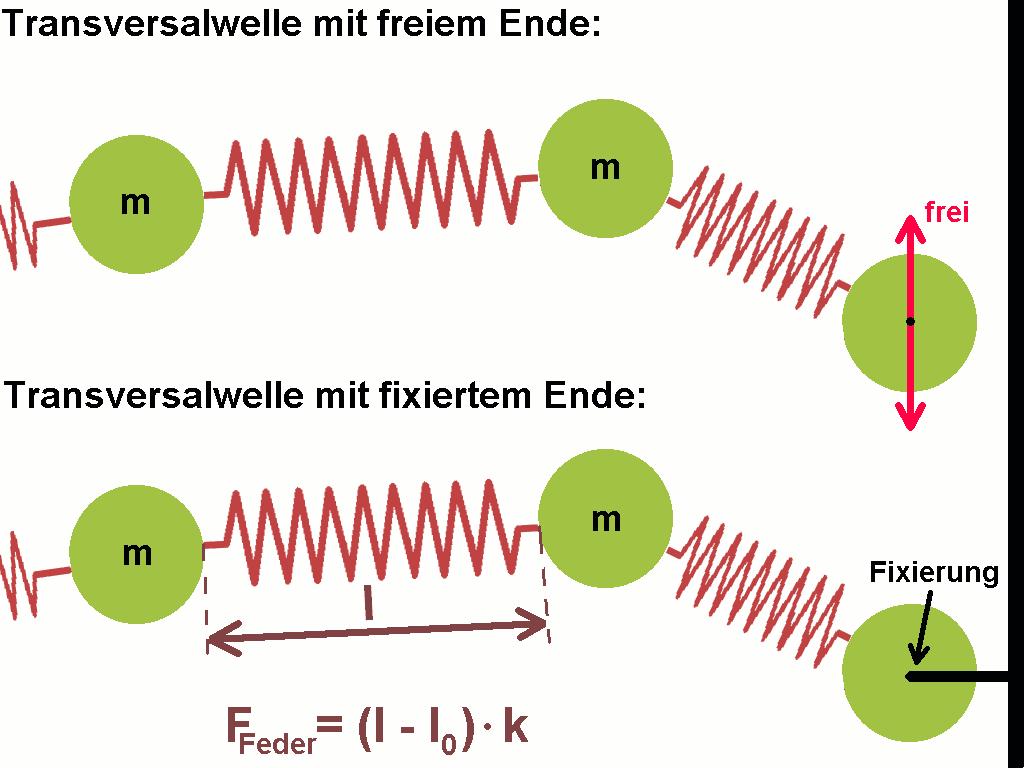
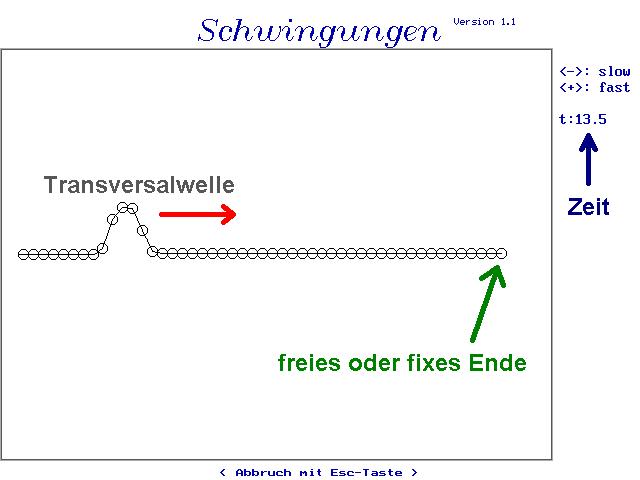
Lenkt man das erste Teilchen ganz links zu Beginn der Simulation einmalig aus, so breitet sich diese Auslenkung/Welle nach rechts mit einer gewissen Geschwindigkeit v aus. Aufgabe meiner Schüler ist es, die Geschwindigkeit v in Pixel/sek in Abhängigkeit von m und k zu ermitteln und dann eine Formel für v(m,k) aufzustellen.

Hier die Ergebnisse der Simulation:
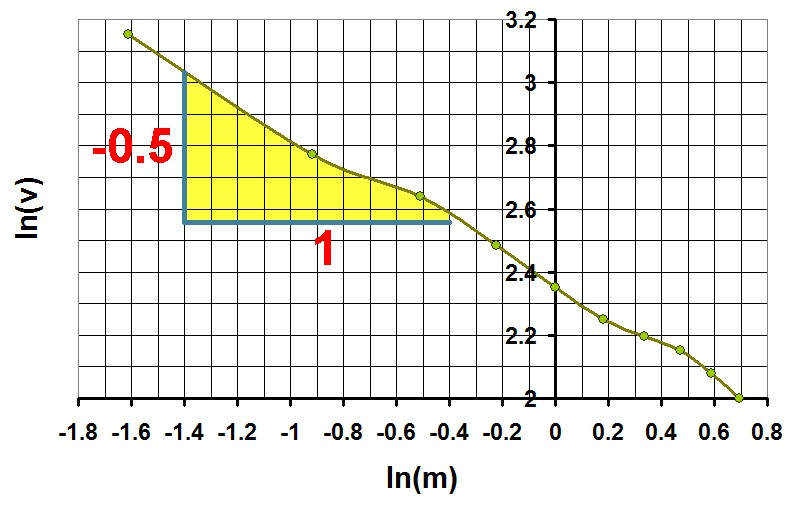
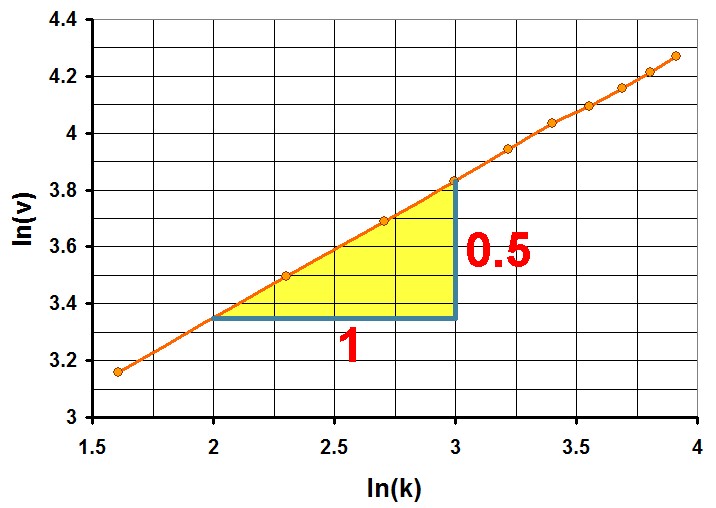
Die Potenz von m beträgt also -1/2 und jene von k genau +1/2. Daher muss die Formel für die Wellengeschwindigkeit v lauten:
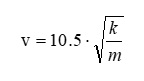
In der Literatur findet man nun folgende Formel für die Schallgeschwindigkeit von Festkörpern:

Die Übereinstimmung ist verblüffend. Anstelle der Federkonstante k tritt die analoge Größe Elastizitätsmodul E und die Masse m wird durch die ebenfalls analoge Größe Dichte ρ ersetzt. Zur Bestimmung des Elastizitätsmoduls muss man also lediglich die Schallgeschwindigkeit im Festkörper/Metall ermitteln. Dies habe ich mit zwei Mikrofonen und der Software Audicity umgesetzt. Dazu habe ich einfach gegen eine 1 m lange Stahlleiste an einem ihrer Enden geschlagen und die beiden Mikrofone im Abstand von 0.9 m an die Metallleiste gekoppelt und die beiden Audiosignale aufgezeichnet:

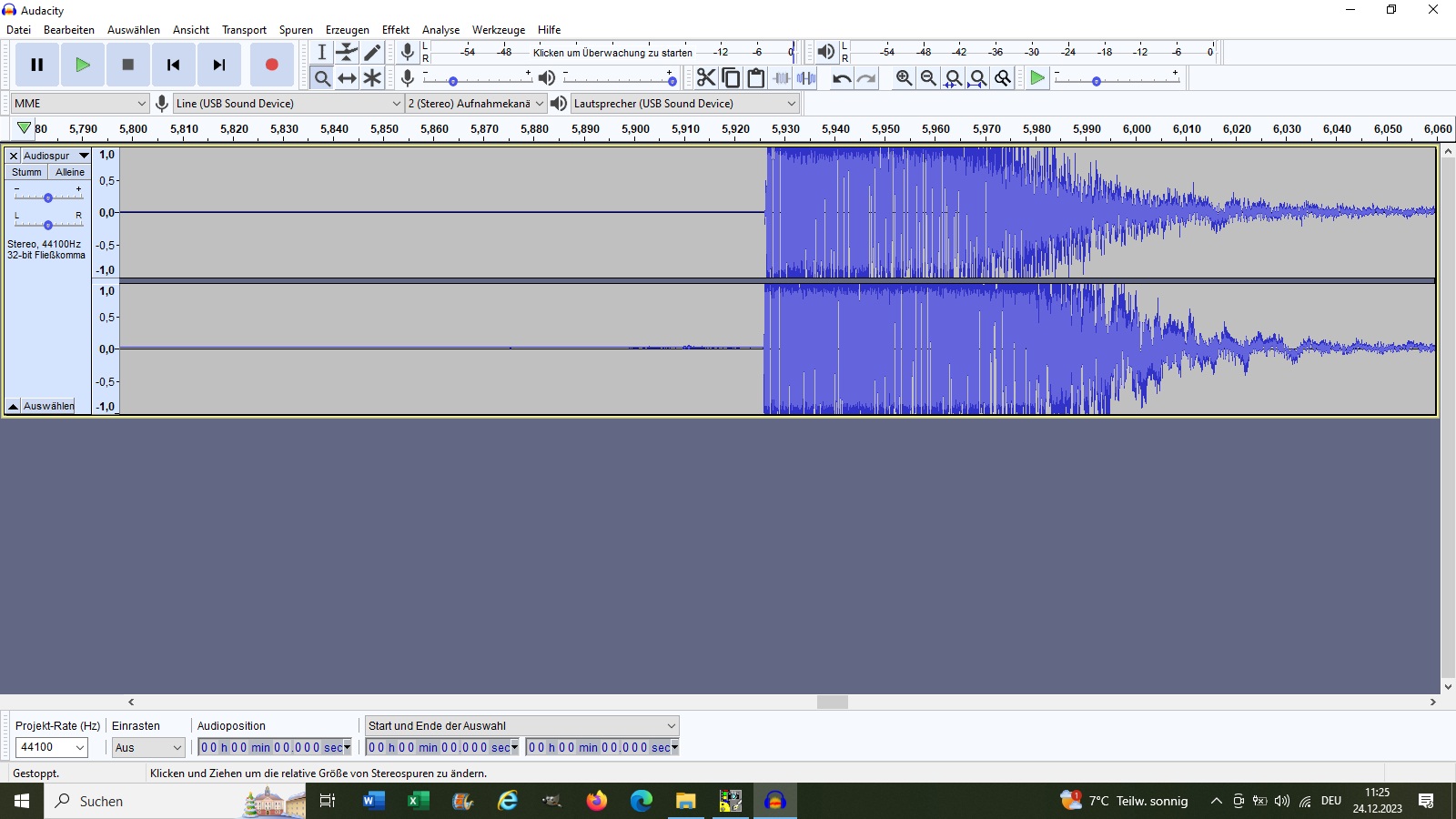
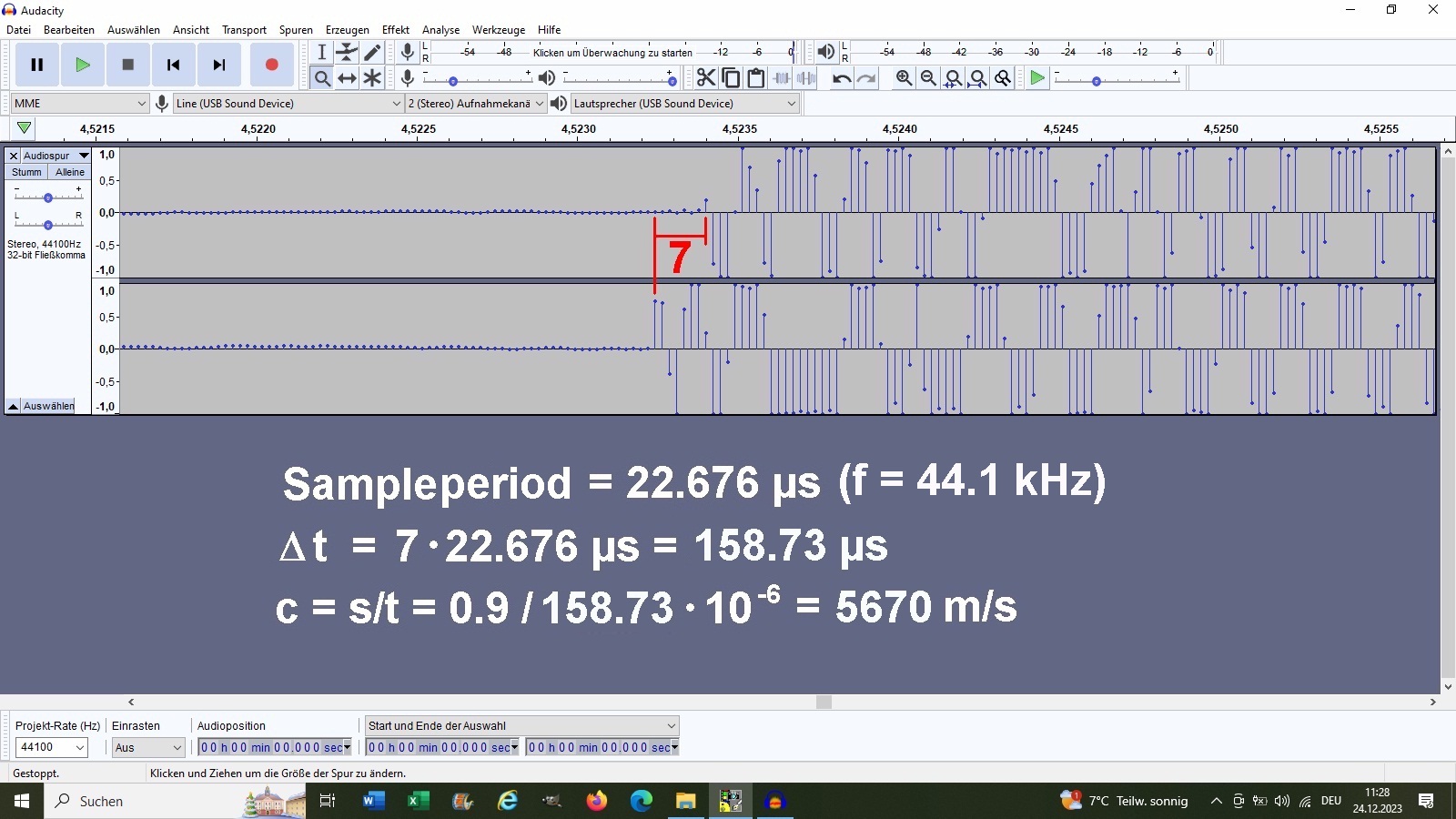
Ich komme auf eine Schallgeschwindigkeit von c = 5670 m/s. Setzt man dies in die obige Formel für v ein, so erhält man mit der Dichte von Stahl (7850 kg/m³) das Elastizitätsmodul E:
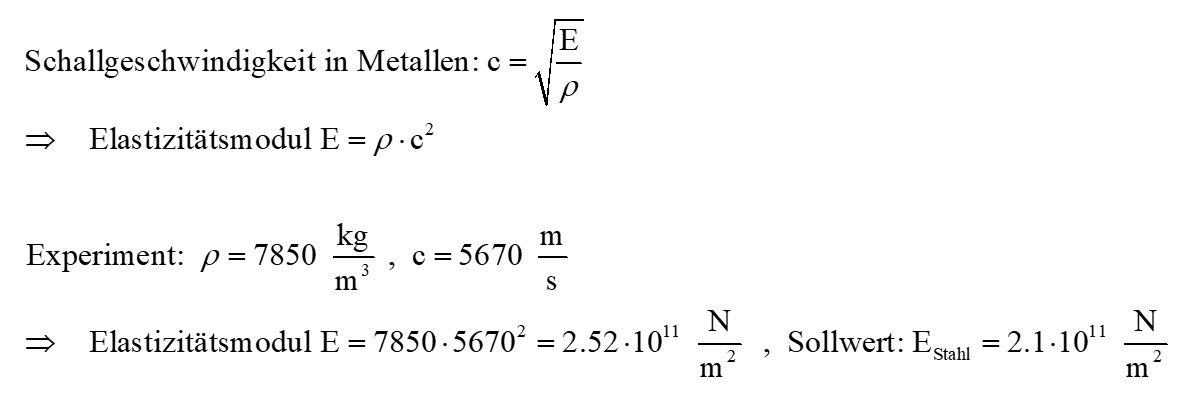
Zum Abschluss wie gewohnt das Youtube-Video:

