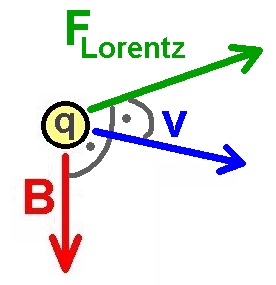
Betastrahlen bestehen ja bekanntlich aus Elektronen bzw. Positronen. Demnach lassen sie sich aufgrund der Lorentzkraft in einem Magnetfeld ablenken. Diesen Umstand nützt man bei der Betaspektroskopie aus.
Das dafür notwendige, homogene Magnetfeld realisierte ich mittels zweier großer 70×15 mm Scheibenmagnete, zwischen denen sich ein Zwischenraum von rund 1 cm Höhe befindet. Genau in diesen Zwischenraum gelangen nun von einer Seite die Betastrahlen. Als Strahlenquelle kommt Strontium-90 zum Einsatz. Dieses geht durch einen Betazerfall mit 546 keV über in Yttrium-90, welches seinerseits durch einen Betazerfall mit 2282 keV zerfällt.














Mein Geigerzähler mit dem Fensterzählrohr ZP1401 (https://stoppi-homemade-physics.de/geigerzaehler-arduino/) ist beweglich am Rand der Scheibenmagnete montiert, sodass verschiedene Ablenkwinkel φ “abgefahren” werden können. Je kleiner der Ablenkwinkel φ, desto größer ist der Impuls p der Elektronen und damit auch ihre Energie. Misst man also die Zählrate in Abhängigkeit vom Ablenkwinkel φ, so erhält man ein Energiespektrum der emittierten Elektronen.
Dieses besteht im Gegensatz zu den Alphastrahlen nicht nur aus einer “Linie”, sondern einem kontinuierlichen Spektrum zwischen E = 0 und einer vom radioaktiven Element abhängigen Maximalenergie E_max. Grund für das Auftreten verschiedener Energien ist der Umstand, dass beim Betazerfall eines Protons nicht nur ein Neutron + Elektron erzeugt werden, sondern noch ein drittes Teilchen, ein sog. Neutrino (genauer ein Anti-Elektron-Neutrino), entsteht. Elektron und Neutrino teilen sich dann die zur Verfügung stehende Energie. Dieses Neutrino wurde bereits im Jahre 1930 durch den berühmten Physiker Wolfgang Pauli prophezeit.

Aus dem Ablenkwinkel φ und den Magnetradius R ergibt sich folgender Bahnradius r innerhalb des Magnetfelds:
r = R / tan(φ/2)
Die für die Kreisbahn notwendige Zentripetalkraft wird durch die Lorentzkraft bereitgestellt. Es gilt daher:
F_zp = m · v² / r = F_L = q · v · B = e · v · B
p = m · v = e · B · r
Nicht relativistisch könnte man mit dem Impuls p die kinetische Energie des Elektrons wiefolgt ermitteln:
E_kin = m · v² / 2 = p² / (2 · m)
Da aber die kinetischen Energien der Betastrahlen im Bereich von > 500 keV liegen und damit bereits der einfachen Ruhemasse eines Elektrons (= 511 keV) entsprechen, muss die kinetische Energie relativistisch hergeleitet werden. Es gilt mit der Ruhemasse m0 des Elektrons:
E_kin = √(m0² ·c^ 4 + p² · c²) – m0 · c²
Für p setzt man in dieser Formel die obigen Ausdrücke p = e · B · r = e · B · R / tan(φ/2) ein. Somit erhält man eine Formel, mit der man aus dem Ablenkwinkel φ die kinetische Energie des Elektrons berechnen kann.


Konkret betrug die magnetische Flussdichte im Zwischenraum 0.15 T. Dieser Wert konnte mit meinem Selbstbau-Teslameter (https://stoppi-homemade-physics.de/magnetometer/) bestimmt werden.
Ein Ablenkwinkel von φ = 40° entspricht bei B = 0.15 T und R = 0.035 m zum Beispiel 3846 keV, ein Ablenkwinkel von φ = 100° jedoch nur noch 905 keV.

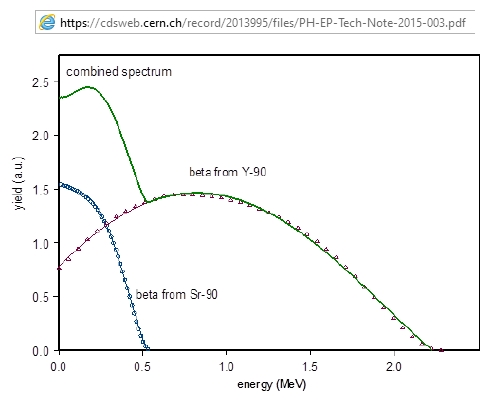
Anhand eines Vergleichs meines Betaspektrums mit einem Graphen aus der Literatur erkennt man die Brauchbarkeit meines Spektroskops. Mein Graph beginnt bei E < 2200 keV aufgrund der Betastrahlen des Yttriums langsam zu steigen bis hin zu einem Maximum bei 1200 keV. Bei Energien um die 300 keV besitzt der Graph dann ein weiteres Maximum, diesmal durch die Betastrahlen des Strontiums.