Ein Körper mit einer bestimmten Temperatur T strahlt elektromagnetische Strahlung, sprich Licht ab. Dies bemerkt man zum Beispiel in einer Schmiede oder in einem Induktionsofen, wenn das Eisenstück auf eine hohe Temperatur gebracht wird.

Das kontinuierliche Spektrum jener Strahlung war um das Jahr 1900 herum bereits bekannt, nur konnte man es nicht zufriedenstellend theoretisch herleiten.
Zwei vorhandene theoretische Näherungen scheiterten, den spektralen Intensitätsverlauf dieser Wärmestrahlung vollständig zu beschreiben. Während das Rayleigh-Jeans-Gesetz nur für große Wellenlängen (niedrige Frequenzen) mit den experimentellen Ergebnissen übereinstimmte und für steigende Frequenzen fälschlicherweise die sog. Ultraviolettkatastrophe vorhersagte, sagte das Wiensche Strahlungsgesetz den richtigen Intensitätsverlauf nur für kleine Wellenlängen (große Frequenzen) voraus.
Bildquelle: https://de.wikipedia.org/wiki/Max_Planck#/media/Datei:Max_Planck_(1858-1947).jpg
Der deutsche Physiker Max Planck widmete sich dieser theoretischen Herausforderung der sog. Schwarzkörperstrahlung. Er postulierte, dass elektromagnetische Strahlung nur in Energieportionen E = h · f = h · c / λ abgegeben werden kann. Dies kann man als Geburtsstunde der Quantenphysik bezeichnen. Unter dieser Annahme erhielt er einen zu erwartenden Intensitätsverlauf, welcher ausgezeichnet mit den experimentellen Ergebnissen übereinstimmte.
Die von ihm hergeleitete Formel für den spektralen Intensitätsverlauf lautet:

M_0_ν(ν, T) ist die Strahlungsleistung, die vom Flächenelement dA im Frequenzbereich zwischen ν und ν + dν in den gesamten Halbraum abgestrahlt wird. Möchte man diese Strahlungsleistung in Abhängigkeit von der Wellenlänge λ darstellen, so benötigt man die Formel für M_0_λ(λ, T). Diese gibt demnach die Strahlungsleistung an, die vom Flächenelement dA im Wellenlängenbereich zwischen λ und λ + dλ in den gesamten Halbraum abgestrahlt wird. Neben der Frequenz ν bzw. der Wellenlänge λ hängt der Intensitätsverlauf entscheidend von der Temperatur T ab:
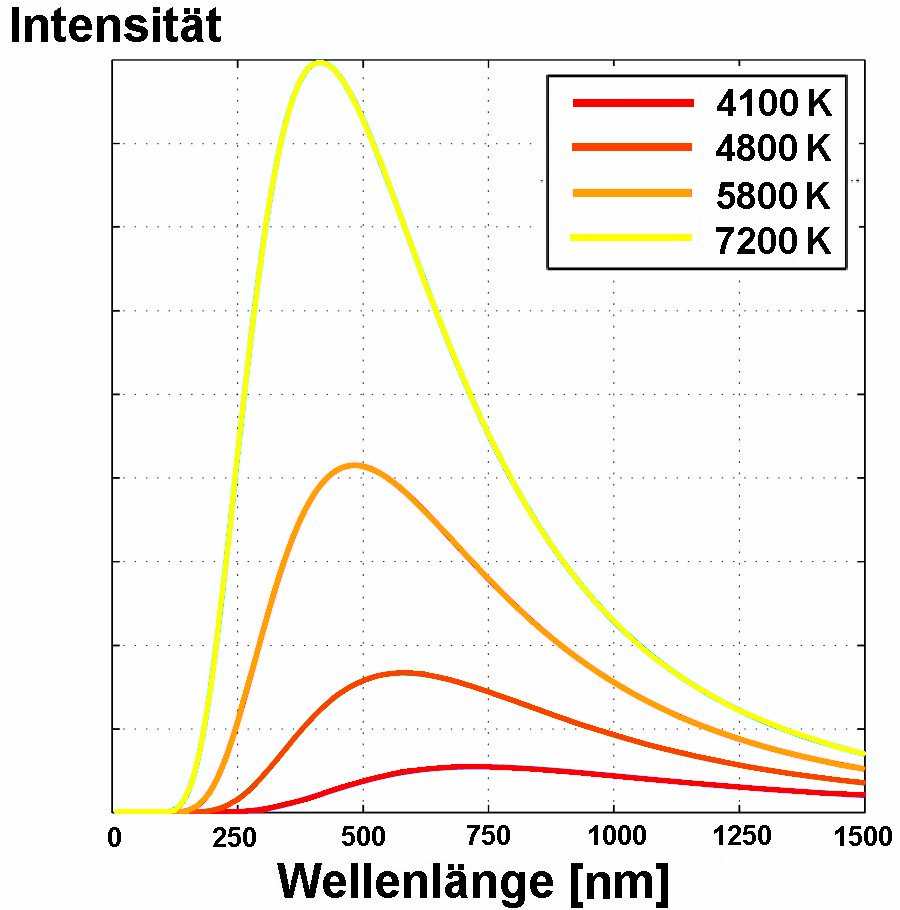
Was erkennt man anhand obiger Spektren? Je höher die Temperatur T, desto weiter verschiebt sich das Strahlungsmaximum nach links in Richtung kleinerer Wellenlänge. Bei einer Temperatur von zum Beispiel 5800 K liegt das Strahlungsmaximum bei einer Wellenlänge von ca. 500 nm. Dies entspricht auch etwa dem Intensitätsverlauf unserer Sonne. Deren Oberflächentemperatur muss daher auch in diesem Bereich liegen. Die einfache Beziehung zwischen λ_max und Temperatur T beschreibt das Wien’sche Verschiebungsgesetz, welches lautet:
λ_max [in μm] = 2897.8 / T [in K]
Bei einer Temperatur von z.B. 3000 K besitzt die Plancksche Strahlungskurve bei λ_max =0.966 μm = 966 nm ihr Maximum.
Experimente
Variante 1: Prismenspektroskop
Wie kann man nun diese Plancksche Strahlungskurve experimentell ermitteln? Als schwarzer Strahler eignet sich etwa eine gewöhnliche Halogenlampe oder Glühbirne. Ich verwende konkret eine Halogenlampe mit 12V/20W. Um diese auch gegebenenfalls austauschen zu können, verwende ich einen entsprechenden Sockel, konkret G4.

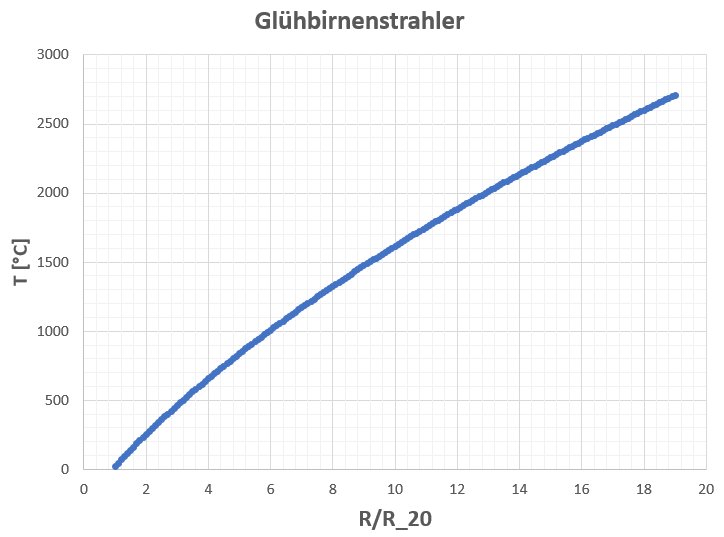
Über die anliegende Spannung U und der Stromstärke I läßt sich der Widerstand R = U/I der Glühwendel berechnen. Dieser Widerstand hängt von der Temperatur T ab. Es gelten dabei folgende Zusammenhänge:
Kennt man das Verhältnis aus aktuellen Widerstand R zum Widerstand R_20 bei Raumtemperatur, so kann man einfach die Temperatur T der Glühwendel berechnen.
Für die Ansteuerung der Halogenlampe verwende ich dasselbe Netzteil wie schon beim Versuch zum Stefan-Boltzmann-Gesetz. Damit lässt sich die Spannung bequem zwischen 1.25 V und 14 V variieren und die jeweilige Spannung und Stromstärke können abgelesen werden.



Um das Lichtspektrum der Halogenlampe in Abhängigkeit von der Temperatur T zu ermitteln, verwende ich als dispersives Medium ein Glasprisma. Dieses gibt es schon für unter 10 Euro auf ebay.com zu kaufen.

Als Lichtdetektor kommt der Sensor TSL252 zum Einsatz. Dieser benötigt lediglich eine Spannungsversorgung zwischen 2.7 und 5.5 V und liefert eine Ausgangsspannung proportional zur Lichtintensität. Betrieben wird der Sensor daher mit einer einzelnen 18650 Liion-Zelle.


Wie sieht nun der gesamte Aufbau zur Messung der Planckschen Strahlungskurve aus? Neben der Halogenlampe, dem Prisma und dem Lichtsensor werden noch 2 Spalte und 2 Linsen benötigt:



Die Linsen (sog. Achromaten mit den Brennweiten f = 26.5 mm und f = 39.5 mm) erhält man etwa bei AstroMedia (https://astromedia.ch/de/produkt-kategorie/materialien-fur-selbermacher/glas-linsen/).
Damit ich bei der Positionierung der Linsen flexibel bin, klebe ich mit 2-Komponentenkleber jeweils einen Magnet seitlich an die Linsen. Diese haften dann stabil aber dennoch flexibel an einem gewöhnlichen L-Winkel aus Metall.

Den verstellbaren Spalt habe ich wie schon bei meinen anderen Spektroskopen mit 2 gewöhnlichen Rasierklingen umgesetzt. Diese liefern einen schön gleichmäßigen Spalt. Dessen Verstellbarkeit ist wichtig, da man einen guten Kompromiss zwischen einem möglichst scharfen Spektrum einerseits und einer ausreichenden Helligkeit andererseits finden möchte.


Um den Spektralverlauf zu erfassen, muss entweder das Prisma gedreht oder der Lichtsensor verschoben werden. Ich habe mich für letzteres entschieden. Damit ich bei mehreren Durchläufen immer genau weiß, wo sich der Sensor gerade befindet, kommt eine digitale Schiebelehre zum Einsatz. Diese wird mit der Grundplatte verschraubt und der Lichtsensor auf den beweglichen Teil der Schiebelehre postiert. So kenne ich immer die exakte Position des Lichtsensors und ich kann Spektren aufnehmen, deren Spektralverlauf nun vergleichbar ist. Dies wird ja benötigt, wenn die Planckschen Strahlungskurven in Abhängigkeit von der Temperatur T der Halogenlampe aufgezeichnet werden.

So, der geplante Aufbau nimmt schön langsam Formen an. Der ganze Aufbau findet auf einer Lochplatte (derzeit 210×100 mm, wird aber wohl eine größere benötigt) Platz und zum Ausrichten der ganzen Elemente verwende ich wie schon erwähnt im Moment einmal Magnete an den Linsen bzw. Stuhlwinkeln.

Ich habe mich zwischenzeitlich auch einmal schlau gemacht, für welche Wellenlängen Glas eigentlich nicht mehr so durchlässig wie im sichtbaren Bereich ist. Wie man anhand der Transmissionskurve von Borosilikatglas sieht, ist die Transmission im für mich wichtigen Spektralbereich von 800 nm bis 1700 nm sehr hoch.
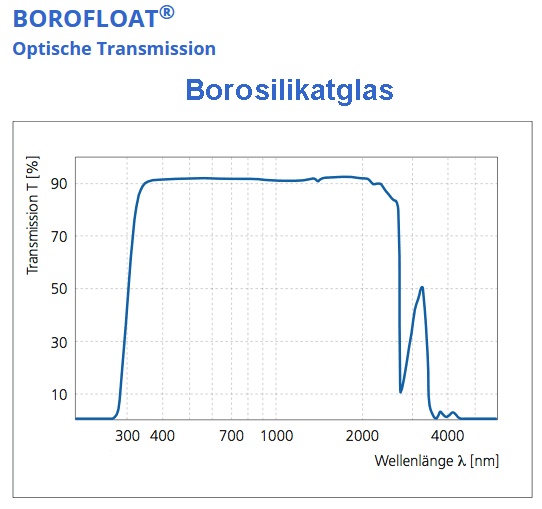
Bildquelle: https://www.pgo-online.com/de/kurven/boro_kurve.html
Die verwendeten Halogenlampen arbeiten ja bei Temperaturen bis maximal ca. 3000 K. Für diese Temperatur befindet sich nach dem Wien’schen Verschiebungsgesetz das Maximum der Planckschen Strahlungskurve bei rund 970 nm. Jetzt ist die im Sensor TSL252 verbaute Silizium-Photodiode nur bis rund 1100 nm sensibel. Dies würde bedeuten, dass ich lediglich bei der Höchsttemperatur von 3000 K die Chance habe, das Maximum schön abzubilden. Bei zum Beispiel 2000 K liegt das Maximum bereits bei 1.45 µm, also im für die Photodiode unsichtbaren Bereich. Ich möchte aber unbedingt das ausgebildete Maximum mit dem Lichtsensor erfassen und nicht bloß die in Richtung größerer Wellenlänge ansteigende Flanke.
Aus diesem Grund habe ich auch eine InGaAs-Photodiode vom Typ LSIPD-A75 auf ebay.com gekauft. Anders als die gewöhnlichen Silizium-Photodioden sind jene aus Indium-Gallium-Arsenid auch im Bereich bis zu ca. 1800 nm sensibel. Und genau dieser Bereich ist ja für die Aufzeichnung der Planckschen Strahlungskurve bei Temperaturen < 3000 K entscheidend.



So, ich habe heute erstmalig versucht, das Spektrum einer weißen LED mit den obigen Linsen (f = 26.5 mm bzw. 39.5 mm) und dem Prisma (brechender Winkel γ = 60°) abzubilden. Das Ergebnis war ernüchternd. Ich erhielt kein wirkliches Spektrum, sondern mehr oder weniger nur einen weißen Strich.
Deshalb betrachtete ich die Sache einmal theoretisch/rechnerisch. Die Dispersionskurve von Quarzglas liefert für den sichtbaren Spektralbereich einen Brechungsindex von n = 1.47 für 400 nm bis n = 1.457 für 640 nm.
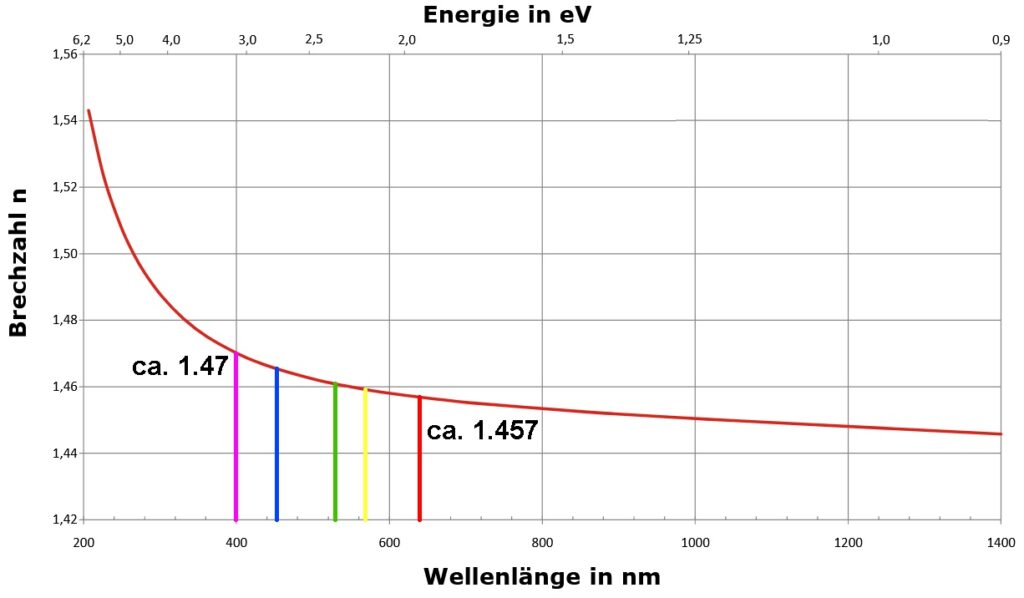
Bildquelle: https://upload.wikimedia.org/wikipedia/commons/8/8e/Komplexe_Brechzahl_von_Siliciumdioxid_300_K.svg
Die Verhältnisse beim Prisma sind wiefolgt:


Mit dieser Formel lässt sich also der Gesamtablenkwinkel φ in Abhängigkeit von der Brechzahl n berechnen. Der zugehörige Graph sieht wiefolgt aus:
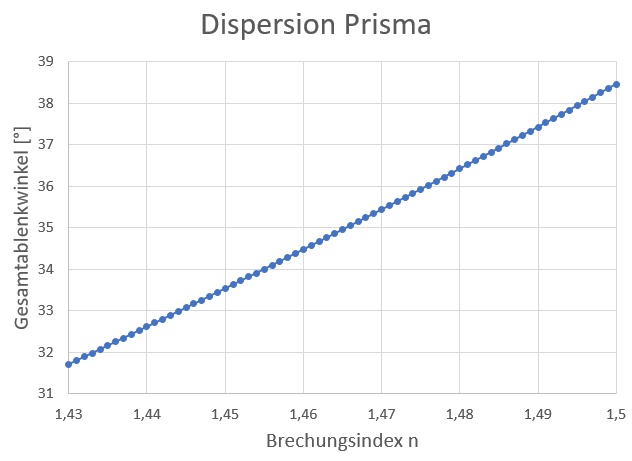
In dem für mich interessanten Brechzahlbereich zwischen 1.457 und 1.47 ergibt sich ein totaler Ablenkwinkel φ von 34.19° bzw. 35.44°. Das bedeutet, dass die Lichtstrahlen von UV (400 nm) und Rot (640 nm) nur mit einem Winkel von 1.25° hinter dem Prisma divergieren. Da hätte ich ehrlich gesagt mit deutlich mehr gerechnet. Bei einer Abbildungslinse mit f = 39.5 mm ergibt dies eine mehr als bescheidene Länge des Spektrums von nur 0.86 mm.

Dies erklärt aber den ersten experimentellen Misserfolg. Da ich die Dispersion des Glasprismas nicht beeinflussen kann (außer ich kaufe mir natürlich eines mit größerer Dispersion), kann ich nur die Brennweite der Abbildungslinse (derzeit eben nur 39.5 mm) vergrößern, um ein längeres Spektrum zu erhalten. Eine Länge von zumindest 3 mm wäre schon schön. Dafür benötigt die Abbildungslinse dann eine Brennweite im Bereich von 12 cm.
Die bereits eingetroffene digitale Schiebelehre zur Positionierung des Lichtsensors besitzt eine Auflösung von 0.1 mm. Dies würde zur erhofften Länge des Spektrums dann gut passen.

Ich habe mir jetzt einmal 2 Linsen mit f = 156.4 mm und f = 182.8 mm bestellt. Damit müsste wie gesagt das sichtbare Spektrum ca. 3.5 -4 mm lang werden.

Für die Abbildungslinse mit längerer Brennweite habe ich mir natürlich auch eine größere Lochplatte (diese misst nun 300 x 200 mm) besorgen müssen.

So, die InGaAs-Photodiode LSIPD-A75 ist angekommen. Falls das mit der Silizium-Photodiode TSL252 als Detektor nichts wird (was ich vermute), so werde ich die LSIPD-A75 mit meinem Transimpedanzverstärker betreiben.




Die neuen Linsen mit größerer Brennweite zur Vergrößerung des Spektrums sind heute angekommen. Ein erster Versuch mit der Linse mit f = 182.8 mm verlief erfolgreich. Das sichtbare Spektrum ist nun ca. 4 mm lang. Wenn ein Wellenlängenbereich von 250 nm (400 nm nach 650 nm) ein rund 4 mm langes Spektrum ergibt, dann kann ich für die restlichen 1000 nm (von 650 nm nach 1650 nm) einmal grob mit ca. 10-12 mm rechnen. Die Dispersionskurve flacht ja bei höheren Wellenlängen deutlich ab (siehe Abbildung weiter oben).
So sehen nun der geplante Aufbau und das erste zufriedenstellende Spektrum aus:


Hier noch die zu erwartenden Planckschen Strahlungskurven für T = 2000 K, 2500 K und 3000 K im Wellenlängenbereich [400 nm,1800 nm]. In dieser Größenordnung liegen die zu erwartenden Temperaturen der Halogenlampe und die von den Photodioden erfassten Wellenlängen.



Der Aufbau ist soweit fertig. Durch die Magnete ist die Justierung der optischen Elemente eigentlich gar nicht so schwierig. Die Schiebelehre am Ort des Spektrums lässt sich auch ausreichend weit verschieben. Jetzt sind nur noch die Intensitätsmessungen in Abhängigkeit von der Temperatur der Halogenlampe ausständig. Die InGaAs-Photodiode LSIPD-A75 spricht wie erwartet nicht auf sichtbares Licht an. Halte ich aber die Fernbedienung vor die Photodiode, so ist eine Ausgangsspannung mit meinem TIA messbar.




Heute konnte ich erste Messungen machen. Die Intensitätssteigerung mit zunehmender Temperatur erfasst die Photodiode natürlich sehr gut. Nur war ich etwas überrascht über die doch nur sehr geringe Verschiebung des Maximums mit ändernder Temperatur. Da sind oft nur 0.1 mm dazwischen. Ich habe mir die Dispersionskurve von Glas daher nochmals angeschaut. Für das Wellenlängenintervall [640 nm, 1400 nm] beträgt die Dispersion nur rund 1°. Dies macht bei einer Brennweite der Abbildungslinse von 182.8 mm eine Länge des Spektrums für diese 760 nm Wellenlängenunterschied von lediglich 3.2 mm. Die Photodiode ist ja bis ca. 1700 nm sensibel. Da kommt dann noch etwa 1 mm dazu, wenn ich bis 1700 nm gehe. Macht also eine Länge des gesamten IR-Spektrums von nur 4.2 mm. Dies verdeutlicht aber die Schwierigkeit der Erfassung der Maximumverschiebung. Zwischen 2000 K und 3000 K wandert dieses nämlich nur um 483 nm in Richtung kürzerer Wellenlänge. Am Ort der Photodiode entspricht dies dann einer Strecke von nur ca. 1.9 mm.


Vor der Photodiode habe ich nun ein Kupferblech mit einem sehr dünnen Schlitz postiert. Die Photodiode selbst besitzt nämlich eine Öffnung von rund 1.5 mm, was viel zu groß für die Messung wäre. Die genauen Messungen der Intensitätsverläufe abhängig von T werde ich dann mit meinem Sohn durchführen und hier veröffentlichen. Ich habe noch bei Roithner-Lasertechnik 3 IR-LEDs mit 1200 nm, 1550 nm und 1650 nm geordert. Damit möchte ich überprüfen, ob erstens die ganze Apperatur für IR durchlässig ist (was sie laut Transmissionskurve für Glas sein müsste) und zweitens ob der IR-Anteil des Spektrums wirklich so dermaßen kurz ist, wie oben berechnet.


Auf der Suche nach einem stärker dispersiven Glas bin ich auf Flintglas gestoßen. Dieses spaltet Licht deutlich stärker auf als etwa gewöhnliches Kronglas, leider aber primär nur im sichtbaren Spektralbereich.
Bildquelle: https://de.wikipedia.org/wiki/Datei:Dispersionskurven.PNG
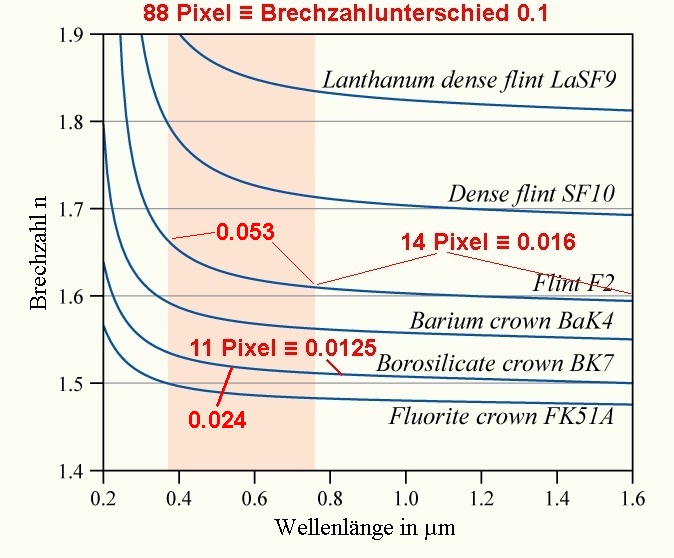
Verglichen mit BK7-Glas beträgt der Brechzahlunterschied Δn für Flintglas im sichbaren Spektralbereich etwa das 2.2-fache. Im für mich interessanten Infrarotbereich zwischen 0.75 µm und 1.6 µm sinkt das Verhältnis leider auf magere 1.28. Egal, ich habe einmal ein Prisma aus Flintglas bestellt. Bei NTL (Naturwissenschaftliche Technische Hilfsmittel) gab es ein verglichen mit anderen Anbietern sehr günstiges Angebot.

Mittlerweile sind die Lichtsensoren vom Typ TSL252R eingetroffen. Wie zu erwarten war, sind sie für diesen Versuch nicht zu gebrauchen. Die Spannungsmaxima am Ausgang des TSL252R befanden sich unabhängig von der Temperatur der Halogenlampe zu nahe neben dem roten Spektralbereich, bei niedriger Temperatur eigenartigerweise sogar noch näher. Bei hohen Temperaturen/Intensitäten kam der Sensor zudem in die Sättigung.

So, das Flintglasprisma von der Lehrmittelfirma NTL (dort ist es für rund 30 Euro inklusive Versand mit Abstand am günstigsten zu beziehen!) ist angekommen. Es hat nicht nur einen hohen Brechungsindex n, sondern auch eine hohe Dichte/Masse. Die Abmessungen des gleichseitigen Prismas betragen: a = 3 cm, h = 3.2 cm. Damit kommt man auf eine Dichte von immerhin 4.64 g/cm³.


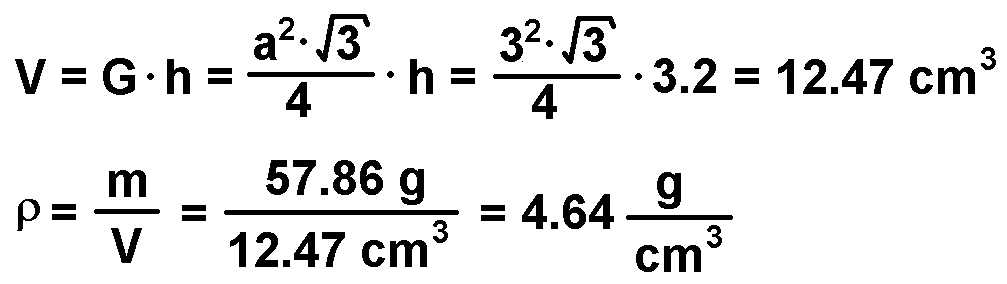
Heute ist der Aufbau des Prismenspektroskops mit dem Flintglas fertig geworden. Wie man anhand der Abbildung erkennen kann, ist die Aufspaltung/Länge des Spektrums beim Flintglas deutlich größer als beim Kronglas. Vor allem im blauen Spektralbereich spaltet das Flintglas durch seine größere Dispersion deutlich mehr auf. Zu hoffen ist, dass es auch im Infrarotbereich das Spektrum etwas in die Länge zieht. Jetzt stehen eigentlich nur mehr die Messungen der Planckschen Strahlungskurven an.



Die Messungen der Planckschen Strahlungskurven mit dem Prismenspektroskop wären im Kasten. Ich habe festgestellt, dass eine minimale Veränderung der Ausrichtung der Photodiode einen starken Einfluss auf den Messwert hat. Deshalb habe ich zum einen die Blende aus Kupferblech entfernt und zum anderen die Photodiode fix mit der Halterung verklebt.
Was die erhaltenen Kurven betrifft, so bin ich nur bedingt zufrieden. Die sehr geringe Verschiebung des Spannungsmaximums/Intensitätsmaximums in Richtung geringerer Wellenlänge mit zunehmender Temperatur (Wien’sches Verschiebungsgesetz) blieb leider bestehen. Den Intensitätszuwachs mit steigender Temperatur (Stefan-Boltzmann-Gesetz) kann man hingegen viel schöner erkennen. Eigenartigerweise liefert die Photodiode auch ohne Bestrahlung einen Basiswert von rund 0,319 V. Diesen habe ich dann einfach von den weiteren Messwerten abgezogen. Die zweite, identische Photodiode zeigt hingegen keinen hohen Basiswert. Defekt dürfte sie jedoch nicht sein, da ich ja einigermaßen schöne Kurven erhalten habe.
Gemessen wurde jeweils immer die Spannung U der Photodiode in Abhängigkeit von der Position x der Photodiode!
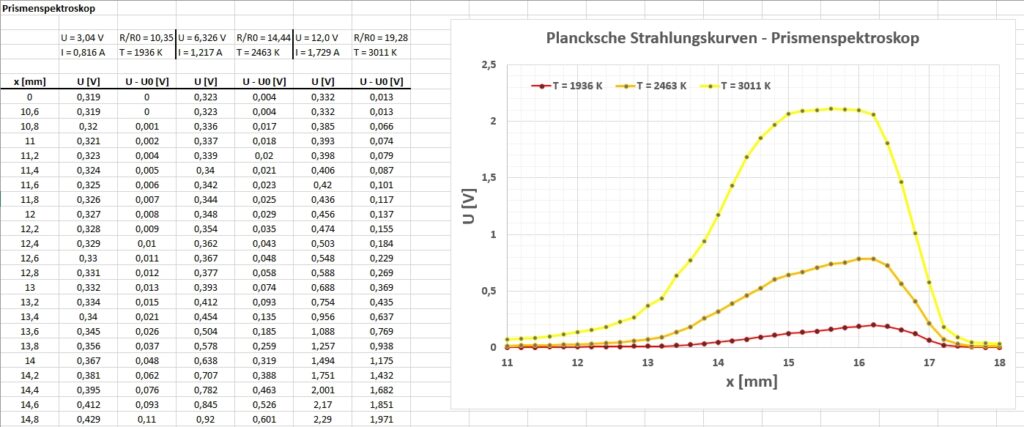

Um sich ein Bild zu machen, welche Position x in etwa welcher Wellenlänge λ entspricht:

Die obigen Messkurven liegen also alle wie erwartet im Infrarotbereich. Leider habe ich keine zur Kalibrierung geeigneten Lichtquellen mit λ > 940 nm. Von daher kann ich die x-Werte > 14 mm keiner Wellenlänge konkret zuordnen.
Variante 2: Gitterspektroskop
Da ein Prisma gerade im Infrarotbereich eine extrem flache Dispersionskurve (siehe oben) besitzt und sich daher der Brechungsindex n nur noch sehr wenig mit der Wellenlänge λ ändert, eignet sich ein solches nicht wirklich gut zur Aufnahme der Planckschen Strahlungskurven. Abhilfe würde hier ein optisches Gitter schaffen.

Ein solches mit 100 Linien/mm habe ich gerade bestellt. Damit beträgt der Beugungswinkel für λ = 400 nm etwa 2.3°, für λ = 800 nm daher 4.6° und für 1700 nm rund 9.8°. Der Infrarotbereich spannt also einen Winkel von 5.2° auf. Bei einem Abstand Gitter-Detektor von rund 10 cm entspricht dies einer Länge des Spektrums von 9.1 mm.
Jetzt hätte man aber mit einem optischen Gitter folgendes Problem: Die Formel zur Berechnung des Beugungswinkels φ lautet ja
sin(φ) = n · λ / d mit n …. Beugungsordnung, λ …. Wellenlänge, d …. Gitterkonstante
Wie man daraus erkennt, sind die beiden Beugungswinkel für n = 2, λ = 600 nm und n = 1, λ = 1200 nm ident. Die verschiedenen Ordnungen überlagern sich also und man würde mit einer für sämtliche Wellenlängen sensiblen Photodiode eine Überlagerung/Summe der einzelnen Beugungsordnungen messen. Die Zuordnung einer Intensität zu einer bestimmten Wellenlänge wäre also nicht mehr möglich.

Jetzt ist die verwendete Photodiode zum Glück nur im Wellenlängenintervall [800 nm, 1700 nm] sensibel. Von daher stören die höheren Ordnungen geringerer Wellenlänge nicht mehr. Das z.B. 3-te Beugungsmaximum von λ = 400 nm stört also nicht mehr das 1-te Beugungsmaximum von λ = 1200 nm, denn die Photodiode LSIPD-A75 ist sowohl im UV-Bereich, also auch im kompletten sichtbaren Spektralbereich absolut blind. Einzig für λ ≥ 800 nm, n = 2 und λ ≥ 1600 nm, n = 1 kommt es zu einer Überlagerung der einzelnen Ordnungen. Dies dürfte aber experimentell verschmerzbar sein.
Ich hoffe natürlich, dass das Beugungsgitter auch im IR-Bereich durchlässig ist. Falls ja, dürfte mit dem Gitterspektroskop ein deutlich längeres IR-Spektrum erzielt werden als mit dem Prismenspektroskop.
Das Gitterspektroskop nimmt schön langsam Formen an. Im Moment habe ich nur ein Beugungsgitter mit 300 Linien/mm. Damit ist die Aufspaltung zu groß und dadurch die Helligkeit zu gering. Ich hoffe, dass dies mit dem 100 Linien/mm-Gitter besser wird. Denn so werde ich Schwierigkeiten haben, mit der Photodiode die geringen Intensitäten zu erfassen. Digitale Schiebelehre und eine zweite LSIPD-A75 habe ich bestellt…



Hier das eben sehr dunkle Spektrum. Und dies bei bereits sehr hoher Spannung der Halogenlampe von 11-12V….

Das Beugungsgitter ist heute angekommen. Eine erste Messung ergab leider eine Gitterkonstante von 0.02 mm, also besitzt es 50 Linien/mm und nicht so wie bestellt 100 Linien/mm. Mmmmmh, dann ist hoffentlich das noch bestellte zweite Gitter richtig.



Jetzt habe ich einmal die Spektren mit dem 50-Linien/mm-Gitter vermessen. Bei einem Abstand Gitter-Schirm von 15 cm komme ich rechnerisch und experimentell auf eine Länge des für mich wichtigen Spektralbereichs [800 nm, 1700 nm] von cirka 0.7 cm. Das wäre gar nicht mal so schlecht. Wenn man aber berücksichtigt, dass der finale Abstand Gitter-Sensor nur rund 11 cm betragen wird, ist es wohl besser das Gitter mit 100 Linien/mm zu verwenden. Damit wird das Spektrum rund 1 cm lang.



Ich habe nun die Schiebelehre vom Prismenspektroskop entliehen und erste Probemessungen mit dem Gitterspektroskop unternommen. Ich erhalte im IR-Bereich ein schönes Spannungsmaximum mit der Photodiode. Was mich aber stört, ist die nur sehr geringe Verschiebung des Strahlungsmaximums mit zunehmender Temperatur in Richtung kleinerer Wellenlänge. Schon beim Prismenspektroskop lag die gemessene Verschiebung im 1/10 mm Bereich. Beim Gitterspektroskop lag sie auch nur bei ca. 0.5 mm, wenn ich die Spannung der Halogenlampe von 6V auf 12V erhöhe. Da hätte ich abermals mit einer deutlich größeren Verschiebung gerechnet. Mit dem 100 Linien/mm Gitter müsste sie sich aber rein theoretisch verdoppeln. Mal schauen…
Ich werde dann die Schiebelehre noch mit einem grünen DPSS-Laser (λ = 532 nm) kalibrieren, damit ich jeder Position (x-Wert) eine Wellenlänge zuordnen kann.


Hier die Tabelle mit den ersten Messwerten:


Wie man sieht, beträgt die Positionsverschiebung des Strahlungsmaximums nur 0.5 mm, obgleich die Temperatur von 2044 K auf 2999 K gewachsen ist. Laut Wienschen Verschiebungsgesetz müsste das Strahlungsmaximum von 1418 nm nach 966 nm gewandert sein.
800 nm entsprechen am Ort der Photodiode einer x-Strecke von rund 5 mm. Demnach müsste die Verschiebung von 1418 – 966 = 452 nm einer Strecke von immerhin 2.825 mm entsprechen. Warum ich nur 0.5 mm messe, ist mir im Moment noch nicht klar.
Eventuell liegt es an der für die Photodiode gebastelten Blende, sodass durch den immer flacheren Winkel bei zunehmender Wellenlänge deutlich weniger Licht den Sensor noch treffen kann. Ich werde es daher einmal ohne Blende probieren.
Und dann hoffe ich noch wie schon gesagt auf eine Verbesserung durch die Verwendung des 100 Linien/mm Gitters.
Mit dem grünen DPSS-Laser (λ = 532 nm) habe ich heute Theorie und Praxis gegenüber gestellt. Die berechneten und gemessenen Positionen der einzelnen Maxima stimmen recht gut überein. Zum Einsatz kam das Gitter mit 50 Linien/mm, der Abstand Gitter-Schirm betrug 120 mm.

Bei Verwendung eines 100 Linien/mm Gitters wird es wohl ziemlich knapp werden mit dem Verstellweg des Sensors auf der Schiebelehre…
Nach 2 Fehllieferungen (habe jeweils ein Gitter mit nur 50 Linien/mm erhalten) kam heute endlich das gewünschte Beugungsgitter mit 100 Linien/mm an. Eine erste, schnelle Messung der Maximumsverschiebung bei verschiedenen Temperaturen stimmt mich zuversichtlich.






Für eine Gitterkonstante d = 10 µm und z.B. λ = 575 nm (= Gelb) beträgt die zu erwartende Ablenkung am Ort der Photodiode 7.5 mm, was sich eigentlich sehr gut mit der nachfolgenden Abbildung deckt:

Heute konnte ich auch mit dem Gitterspektroskop die Planckschen Strahlungskurven aufnehmen. Die an der Photodiode gemessenen Spannungen sind deutlich geringer als beim Prismenspektroskop, da sich ja beim Gitter die Gesamtintensität auf viele Maxima (vor allem das 0-ter Ordnung) verteilt. Ein großer Vorteil des Gitters ist es, dass ich der Position x der Photodiode sehr einfach eine Wellenlänge λ zuordnen kann. Durch die ungleichmäßige Dispersion beim Prisma ist dies dort nicht so ohne weiteres möglich.
Hier nun die erhaltenen Planckschen Strahlungskurven für 4 verschiedene Temperaturen:


Die Verschiebung der Maxima in Richtung kürzerer Wellenlänge bei steigender Temperatur ist auch beim Gitterspektroskop schwach ausgeprägt aber immerhin zu erkennen.

