Lichtteilchen (Photonen) besitzen ja die Ruhemasse 0. Daher können sie sich auch mit Lichtgeschwindigkeit fortbewegen. Denn jede auf Lichtgeschwindigkeit beschleunigte Masse m ungleich 0 würde eine unendlich große kinetische Energie besitzen. Spannend ist aber der Umstand, dass Photonen trotz der Ruhemasse 0 einen Impuls p besitzen. Dies widerspricht der klassischen Formel für den Impuls p mit p = Masse m · Geschwindigkeit v, wonach ein Körper mit der Masse 0 immer den Impuls p = 0 besitzt.
Wir kennen aber die berühmte Einsteinbeziehung E = m·c² zwischen der Masse m und der Energie E. Demnach gilt für das Produkt m·c = E/c. Dieses Produkt m·c ist aber gleich dem Photonenimpuls p. Daraus folgt der Zusammenhang zwischen Photonenimpuls p und Photonenenergie E und zwar p = E/c.
Eine weitere Möglichkeit der Herleitung geht vom Zusammenhang zwischen dem Impuls p, der Energie E und der Ruhemasse m0 aus:
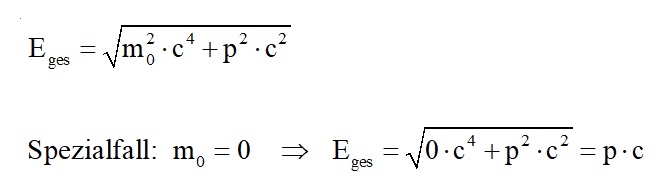
Mit zunehmender Energie der Lichtteilchen steigt also ihr Impuls p. Zumindest dieser Zusammenhang ist auch klassisch nachvollziehbar. Die Energie eines Photons hängt ja direkt mit der Frequenz f nach E = h·f zusammen. Es gilt also auch h·f = p·c. „Blaue“ Photonen besitzen demnach einen größeren Impuls als „rote“.
Lichtteilchen weisen also einen Impuls auf. Dies zeigt sich etwa bei der sog. Laserlevitation, welche ich hier experimentell umgesetzt habe: https://stoppi-homemade-physics.de/laserlevitation/
Die berühmte Beziehung von de Broglie verknüpft ja als Hauptaussage des Welle-Teilchen-Dualismus eine typische Welleneigenschaft (Wellenlänge λ) mit einer typischen Teilcheneigenschaft (Impuls p). Sie lautet:
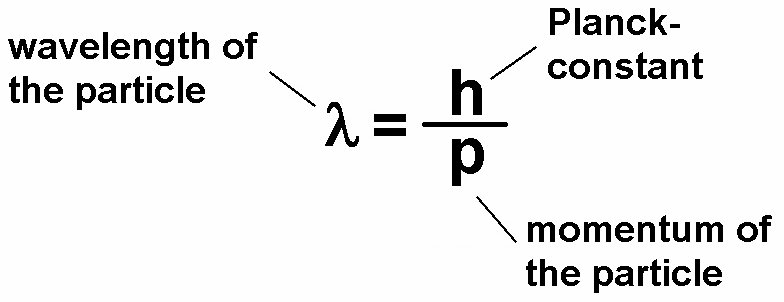
Eine Umformung liefert unter Verwendung der Wellengleichung dann genau wieder den obigen Ausdruck:
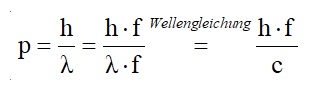
Wie soll nun ein weiterer experimenteller Beweis des Lichtimpulses aussehen? Ich habe hier meine µg-Waage präsentiert: https://stoppi-homemade-physics.de/%c2%b5g-waage/.
Mit dieser Waage bin ich imstande geringste Massen/Kräfte nachzuweisen. Geeicht habe ich diese Waage mit einem 1 x 1 mm großen Papierquadrat. Bei einer üblichen Masse von 70 g/m² wiegt dieses kleine Papierquadrat lediglich 70 µg. Damit erhielt ich eine am Multimeter angezeigte Ausgangsspannung von 9 mV. Die Empfindlichkeit der Waage beträgt also genau 9 / 70 = 0.129 mV/µg.


Leuchte ich nun mit einem sehr starken Laser auf die kleine Pfanne am Ende des Zeigers, so müsste durch den Impuls der Photonen eine Kraft bzw. Masse angezeigt werden. Diese gilt es einmal abzuschätzen:


Bei der vollständigen Reflexion eines Lichtteilchens/einer Masse wird der doppelte Impuls an den Stoßpartner übertragen. Dies ergibt sich ganz einfach aus dem Impulserhaltungssatz.
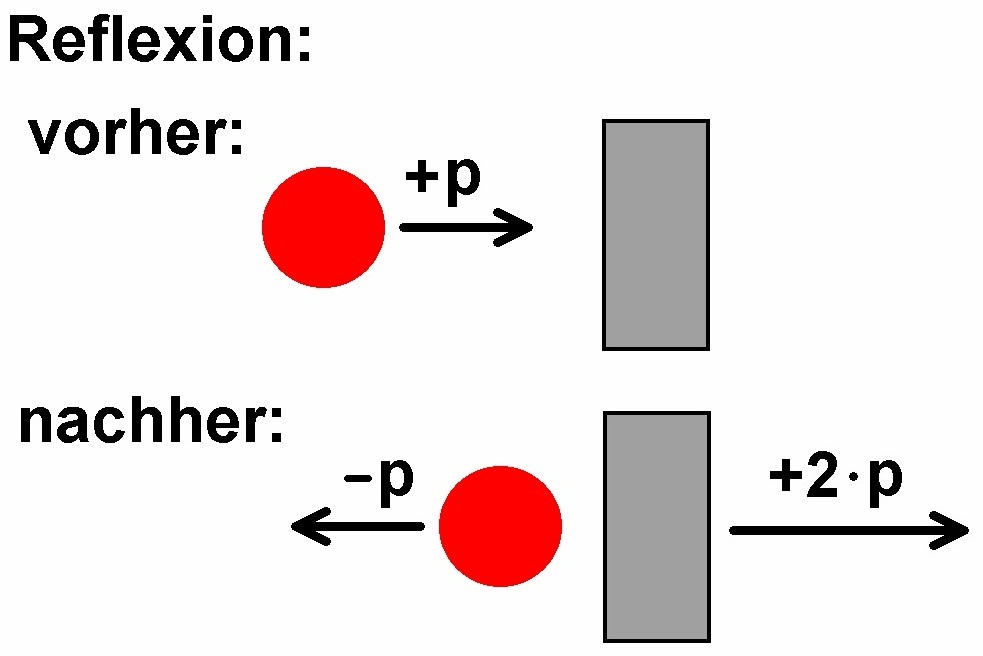
Wie man anhand folgender Tabelle sehen kann, benötigt man für einen einigermaßen messbaren Effekt einen sehr starken Laser.

Ein auf die Pfanne gerichteter 10W-Laser sollte also einer Masse von immerhin 6.7 µg entsprechen. Bei meiner Waage würde man also eine Ausgangsspannung von 0.129 · 6.7 = 0.8643 mV erwarten. Dies ist zwar wenig aber durchaus ohne größere Probleme messbar. Zum Erfassen dieser Spannung verwende ich einen Arduino in Kombination mit dem AD-Wandler ADS1115. Dieser hat in der empfindlichsten Einstellung immerhin eine Auflösung von 0.0078125 mV.
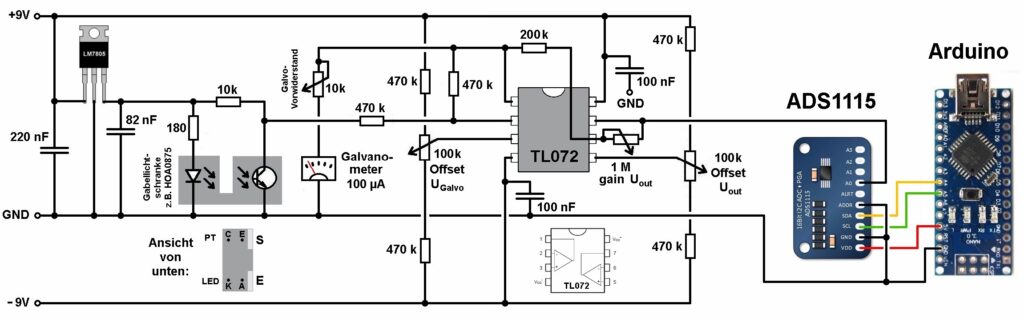

Damit ich eine größere Messsicherheit erhalte, erzeuge ich den Mittelwert über 1000 Spannungsmessungen. Damit müsste der Effekt durch den Laser eigentlich ohne Probleme erfassbar sein, wenn nicht andere Effekte wie Konvektion durch Erwärmung der Pfanne mir einen Strich durch die Rechnung machen. Konvektion müsste aber eher die erwärmte Pfanne in der aufsteigenden Luft nach oben drücken, die angezeigte Masse also eher reduzieren und nicht erhöhen wie durch den Strahlungsdruck erwartet. Aber das werden wir nachher sehen… 😉
Auf aliexpress gibt es für rund 60 Euro bereits so starke Laser wie benötigt:
Hier also der sehr einfache Versuchsaufbau:
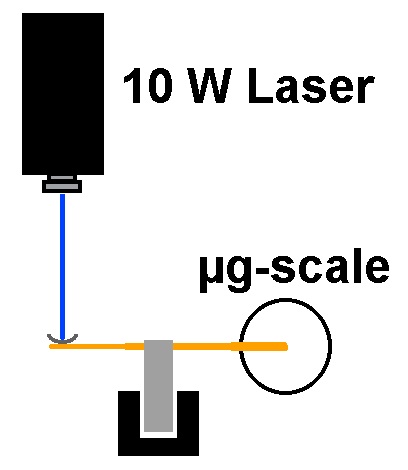
Wenn man an Lichtdruck denkt, fällt einem sofort eine Lichtmühle (Radiometer, https://de.wikipedia.org/wiki/Radiometer) ein. Man könnte meinen, dass wiederum der Impuls der Lichtteilchen die Rotation der Lichtmühle verursacht. Dies ist aber nicht der Fall. Denn würde tatsächlich der Photonenimpuls dafür verantwortlich sein, so müsste die zur Lichtquelle zugewandte dunkle Fläche das Photon absorbieren und daher für einen Impulszuwachs 1·p sorgen. Bei der reflektierenden Fläche wäre der Impulsübertrag aber doppelt so groß, genau 2·p. Daher müsste sich die reflektierende Fläche der Lichtmühle von der Lichtquelle wegdrehen und die dunkle Fläche auf die Lichtquelle zukommen. In der Praxis ist es aber genau umgekehrt. Daher kann der Lichtdruck keine Rolle spielen.

Bildquelle: https://en.wikipedia.org/wiki/Radiometer
Es ist vielmehr eine thermische Angelegenheit. Die dunkle Fläche der Lichtmühle ist geringfügig wärmer. Dadurch schwingen auf dieser Seite die Atome etwas stärker. Luftmoleküle, die nun auf die dunkle Fläche stoßen, werden etwas stärker reflektiert, als dies bei der reflektierenden Fläche der Fall ist. Daher erhält die dunkle Fläche einen stärkeren Rückstoß und die Lichtmühle dreht sich mit der dunklen Fläche vom Licht weg.
Das sehr simple Arduino-Programm zur Messung der geringen Ausgangsspannung ist soweit fertig. Getestet habe ich es mit einer 9V-Batterie an einem 1:1000 Spannungsteiler. Die angezeigte Spannung ist der Mittelwert aus 1000 Einzelmessungen.



In der zweiten Zeile des Displays wird die Spannungsänderung gegenüber der letzten Messung angezeigt. Dies soll den Ablesevorgang erleichtern, wenn ich den Laser zugeschaltet habe…

Arduino-Programm:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 |
#include <Wire.h> #include <Adafruit_ADS1015.h> #include <LiquidCrystal_I2C.h> //Adafruit_ADS1015 ads1015; // Construct an ads1015 at the default address: 0x48 //Adafruit_ADS1115 ads1115(0x49); // construct an ads1115 at address 0x49 Adafruit_ADS1115 ads1115; // Construct an ads1115 at the default address: 0x48 LiquidCrystal_I2C lcd(0x27,16,2); // set the LCD address to 0x27 for a 16 chars and 2 line display. ACHTUNG: Adresse kann auch 0x3F sein !!! // Anschlüsse: // GND - GND // VCC - 5V // SDA - ANALOG Pin 4 // SCL - ANALOG pin 5 int16_t adc0, adc1, adc2, adc3; float voltage, voltage_old; int i; byte delta[8] = { B00100, B00100, B01010, B01010, B10001, B10001, B11111, B00000 }; void setup(void) { Serial.begin(9600); //ads1015.begin(); // Initialize ads1015 ads1115.begin(); // Initialize ads1115 // The ADC input range (or gain) can be changed via the following // functions, but be careful never to exceed VDD +0.3V max, or to // exceed the upper and lower limits if you adjust the input range! // Setting these values incorrectly may destroy your ADC! // ADS1015 ADS1115 // ------- ------- // ads1115.setGain(GAIN_TWOTHIRDS); // 2/3x gain +/- 6.144V 1 bit = 3 mV 0.1875 mV (default) // ads1115.setGain(GAIN_ONE); // 1x gain +/- 4.096V 1 bit = 2 mV 0.125 mV // ads1115.setGain(GAIN_TWO); // 2x gain +/- 2.048V 1 bit = 1 mV 0.0625 mV // ads1115.setGain(GAIN_FOUR); // 4x gain +/- 1.024V 1 bit = 0.5 mV 0.03125 mV // ads1115.setGain(GAIN_EIGHT); // 8x gain +/- 0.512V 1 bit = 0.25 mV 0.015625 mV // ads1115.setGain(GAIN_SIXTEEN); // 16x gain +/- 0.256V 1 bit = 0.125 mV 0.0078125 mV ads1115.setGain(GAIN_SIXTEEN); // 16x gain +/- 0.256V 1 bit = 0.0078125 mV lcd.begin(); // initialize the lcd lcd.backlight(); lcd.setCursor(0,0); lcd.print("Voltmeter"); lcd.setCursor(0,1); lcd.print("Lichtdruck"); delay(3000); lcd.setCursor(0,0); lcd.print(" "); lcd.setCursor(0,1); lcd.print(" "); voltage_old = 0.0; lcd.createChar(0, delta); } void loop(void) { voltage = 0.0; for (i = 1; i <= 1000; i++) { adc0 = ads1115.readADC_SingleEnded(0); voltage = voltage + adc0 * 0.0078125; //delay(20); } voltage = voltage / 1000.0; Serial.print(" U = "); Serial.print(voltage,4); Serial.println(" mV"); lcd.setCursor(0,0); lcd.print("U = "); lcd.print(voltage,4); lcd.print(" mV "); lcd.setCursor(0,1); lcd.write(0); lcd.print("U = "); lcd.print(voltage - voltage_old,4); lcd.print(" mV "); voltage_old = voltage; //delay(1000); } |
Leider habe ich im Moment nur relativ schwache Laser zum Testen zuhause. Der stärkste war ein roter Laser mit rund 150 mW. Damit zeigte sich keinerlei Veränderung der Ausgangsspannung.




Bevor ich den 20W-Laser (optischer Output allerdings „nur“ rund 7W) ordere, probiere ich es noch mit einer 2W-Laserdiode. Diese habe ich auf aliexpress für rund 24 Euro gekauft.
Bei einer angenommenen optischen Leistung von 1.5W müsste ich folgende Spannungserhöhung erwarten können:

Inzwischen ist die blaue Laserdiode aus China eingetroffen. Dies ist wohl für einige Zeit die letzte Lieferung über aliexpress. Denn mit 1. Jänner 2023 versenden die Aliexpress-Händler aufgrund einer Verpackungsverordnung nicht mehr nach Österreich. Ich hoffe, dies ist nur temporär…



Ich konnte am Wochenende den Versuch durchführen. Zunächst musste ich allerdings feststellen, dass die Spannung am Ausgang der µg-Waage trotz der Mittelwertsbildung (1000 Werte) zu sehr schwankte. Daher verwende ich nun einen einfachen Tiefpassfilter bestehend aus einem 10 kΩ Widerstand und einem 100 nF Kondensator. Damit blieb dann die zu messende Spannung relativ konstant.
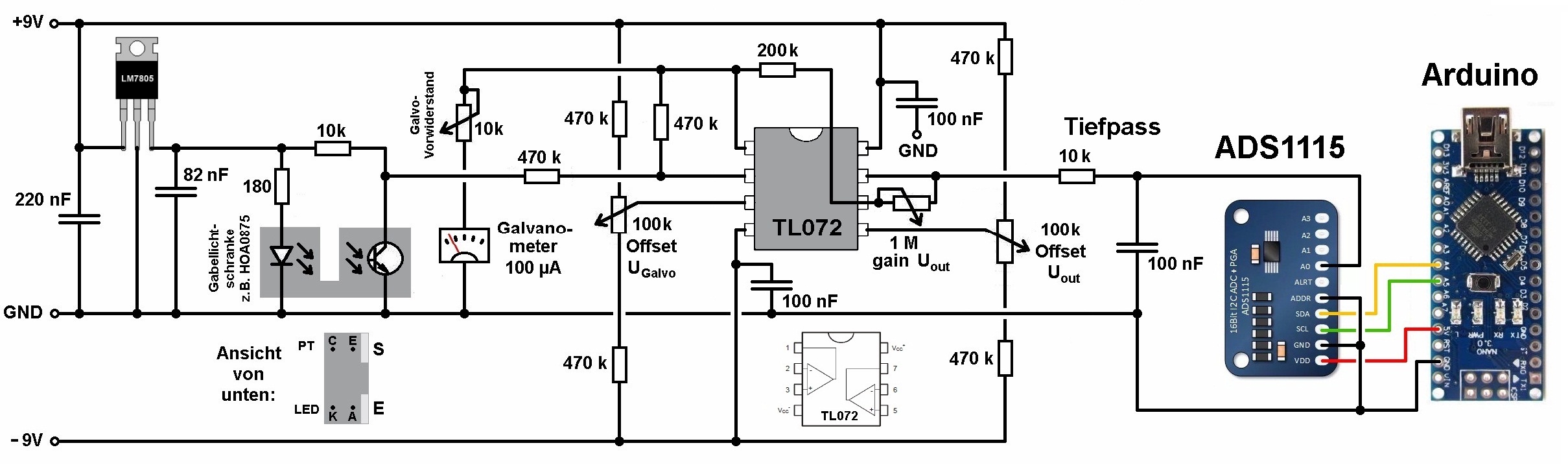


Den Laser betreibe ich bei einem Strom von 1.1 A. Damit sollte die optische Leistung im Bereich von 1.8 W liegen.




Als ich dann den Laser einschaltete, konnte ich tatsächlich eine Spannungserhöhung im Bereich von 0.15 mV beobachten. Dies würde sich sehr gut mit der obigen Abschätzung des zu erwartenden Spannungsanstiegs (+0.13 mV bei einer angenommenen Laserleistung von 1.5 W) decken. Bei wieder ausgeschalteten Laser ging diese Spannung zurück. Ich muss aber bemerken, dass es auch ohne eingeschalteten Laserlicht teilweise zu ähnlichen Änderungen der Ausgangsspannung kam. Aber scheinbar konnte ich tatsächlich den Impuls von Lichtteilchen/Photonen messen, Heureka 🙂

Hier noch wie versprochen das Youtube-Video:

