
Quelle: Wikipedia
Die Bragg-Gleichung, auch Bragg-Bedingung genannt, wurde 1912 von William Lawrence Bragg entwickelt. Er bekam dafür 1915 den Nobelpreis für Physik verliehen. Sie beschreibt, wann es zu konstruktiver Interferenz von Wellen bei Streuung an einem dreidimensionalen Gitter kommt. Sie erklärt die Muster, die bei der Beugung von Röntgenstrahlung an kristallinen Festkörpern entstehen, aus der strengen Periodizität von atomaren Gitterebenen.
Angeregt durch eine Veröffentlichung Max von Laues arbeitete Lawrence Bragg von 1912 bis 1914 zusammen mit seinem Vater an der Untersuchung von Kristallen mit Röntgenstrahlung. Er fand die berühmte Bragg-Gleichung 1912, die nach den beiden Physikern benannt wurde, und nutzte sie gemeinsam mit seinem Vater, der den Röntgenspektrografen entwickelte, zur Untersuchung verschiedener Kristalle.
Beim Versuch zur Elektronenbeugung an Graphit (https://stoppi-homemade-physics.de/elektronenbeugung/) kamen wir bereits einmal in Kontakt mit der Braggreflexion. In diesem Fall war es aber keine elektromagnetische Strahlung (z.B. Röntgenstrahlung), welche reflektiert wurde, sondern Materiewellen (schnelle Elektronen). Hier soll es nun um niederenergetische Gammastrahlung gehen, welche an einem Einkristall reflektiert/gebeugt wird.


Als Strahlungsquelle versuche ich es mit Americium-241. Dies ist ein Alpha- und Gammastrahler, wobei die Gammaquanten eine Energie von rund 60 keV besitzen.
Achtung: Im Umgang mit radioaktiven Proben ist größte Sorgfalt und Vorsicht geboten. Jeglicher direkte Kontakt der Probe mit der Umgebung und dem menschlichen Körper ist auszuschließen!
Wie kann man sich nun die Braggreflexion vorstellen? Treffen elektromagnetische Strahlung oder Materiewellen auf ein Kristallgitter mit der Gitterkonstante k, so kommt es nur dann zu einer Reflexion nach dem bekannten Gesetz Einfallswinkel = Ausfallswinkel, wenn die sog. Bragg-Bedingung erfüllt ist:

Der Wegunterschied 2·Δs der beiden Strahlengänge muss also ein ganzzahliges Vielfaches der Wellenlänge λ sein (= konstruktive Interferenz). Trifft die Strahlung unter dem Winkel φ auf den Kristall. so muss sich der Detektor (in meinem Fall ein Geiger-Müller-Zählrohr) bei einem Positionswinkel 2·φ befinden. Aber selbst dann erhält man in den meisten Fällen kein Signal, außer in den sog. Glanzwinkel, wenn eben die Braggbedingung erfüllt ist.

Als Einkristall verwende ich Lithiumfluorid. Dieser wurde mir dankenswerterweise gratis von der deutschen Firma Korth-Kristalle (https://www.korth.de/) bereitgestellt. Vielen herzlichen Dank dafür, ich habe mich riesig darüber gefreut. 🙂


Die Wahl fiel deshalb auf Lithiumfluorid, da es mit d = 201,38 pm eine vergleichsweise geringe Gitterkonstante aufweist und dadurch die Glanzwinkel größer werden (vgl. obige Formel sin(φ) = n·λ/2·d). Dies muss ich in meinem Fall beachten, da ich anstelle von Röntgenstrahlung deutlich energiereichere Gammastrahlung eben mit 60 keV verwende. Eine höhere Energie der Quanten hat aber eine geringere Wellenlänge und damit auch geringere Glanzwinkel zufolge. Selbst bei Verwendung von LiF betragen dann in meinem Fall die Glanzwinkel nur Vielfache von 3°, was sehr wenig ist. Würde ich anstelle von Lithiumfluorid zum Beispiel Natriumchlorid (Gitterkonstante 281,97 pm) verwenden, so wären die zu erwartenden Winkel noch einmal deutlich geringer.

Von der Firma FIAS Firsching Analytical Systems (http://www.fias.at/) bekam ich dankenswerterweise 5 Stück NaCl-Einkristalle gratis zugesandt. Vielen lieben Dank dafür, freue mich ebenfalls riesig darüber…



Auf willhaben.at hatte ich mir zuvor bereits Halit (also Steinsalz) gekauft. Dabei achtete ich auf möglichst schöne Kristallebenen…

Ich werde es aber wie bereits erwähnt mit LiF probieren. Wenn ich es damit nicht schaffe, die Glanzwinkel von nur 3° aufzulösen, dann geht es mit NaCl leider erst recht nicht…



Der mechanische Auufbau erfolgt unter anderem mit Matador-Holzspielsachen (https://www.matador.at/Produkte/Explorer-5/Einzelteile-Ersatzteile:::1_3_55.html). Dieses in Österreich gefertigte Spielzeug habe ich schon mehrmals bei meinen Projekten (z.B. Rutherfordstreuung oder Betaspektroskopie) erfolgreich verwendet.
Zur Einstellung der beiden Winkel (φ für Einkristall bzw. 2·φ für Geigerzähler) habe ich mir auf ebay.com solche Winkellineale besorgt:




Schön langsam geht es hier weiter mit dem mechanischen Aufbau:












Zum Abschirmen der schwachen Gammastrahlung verwende ich Walzblei mit einer Dicke von insgesamt 3 x 1 mm. Damit dürfte laut Grafik für eine ausreichende Abschwächung gesorgt sein…



Zum Kollimieren der Gammastrahlen habe ich 2 mm kleine Löcher ins Walzblei gebohrt:

Hier der soweit fertige mechanische Aufbau:



So, gestern und heute konnte ich erste Messungen durchführen. Zuerst habe ich einmal den Strahlungshintergrund mit meinem Geigerzähler bestimmt. Ich komme auf einen Background von 22.761 counts per minute (cpm), wobei die Messzeit fast 2 Stunden betrug.


Dann habe ich die Zählrate in Abhängigkeit vom Winkel ermittelt. Die Schrittweite betrug jeweils 0.5° und die Messzeiten lagen zwischen 16 min und fast einer Stunde.




Hier nun die Messergebnisse:

Zu erwarten wäre folgender Graph:

Resümee: Mein Gammastrahler ist deutlich zu schwach. Deshalb liegen die Zählraten auch nur minimal über dem Strahlungshintergrund. Würde ich aber einen deutlich stärkeren Strahler besorgen so hätte dieser wohl eine größere aktive Fläche und der Effekt würde verpuffen. Ich lasse ja durch die Kollimierung mit den Bleiblenden nur einen sehr engen Strahl auf den Lithiumfluoridkristall zu. Zweitens ist die Wellenlänge der Gammastrahlen für dieses Experiment zu gering. Dadurch sind die Glanzwinkel auch sehr klein im Bereich von Vielfachen von 3°. Dadurch wird die Messung nicht unbedingt leichter. Alles in allem hat das Experiment nicht ganz so funktioniert wie erhofft. Dies war mir aber nach ersten Berechnungen und Abschätzungen schon im Vorhinein klar. Aber auch das gehört zur Physik und bei weitem nicht jedes Experiment funktioniert so, wie man sich das ausgedacht hat. 😉
Zum Abschluss noch das Youtube-Video:
Hier auf dieser Seite (https://www.forphys.de/Website/qm/braggdual1.html) bin ich auf ein Experiment zur Bragg-Reflexion mit Ultraschall gestoßen.

Quelle: https://www.forphys.de/Website/qm/braggdual1.html
Dies kannst du doch auch probieren, dachte ich mir wie so oft. 40 kHz-Ultraschallmodule habe ich ja noch genügend zuhause und den Rest besorge ich halt wie üblich auf Amazon oder anderen Verkaufsportalen. Das Atomgitter möchte ich z.B. aus Schaschlikspießen und Holzkugeln basteln:


Für die Kollimierung bzw. Fokusierung des Ultraschalls habe ich solche Zigaretten-Solaranzünder bestellt:

Die Ultraschallsensoren entnehme ich den bekannten HC-SR04-Arduino-Modulen, welche man schon um ca. 4 Euro zu kaufen bekommt. Angesteuert wird die Senderkapsel mittels Arduino Nano und einem 40 kHz-Signal, welches zunächst einen L298N-fullbridge-Motortreiber speist, an dem dann die US-Kapsel hängt.



Hier gleich der kurze Arduino-Code:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
byte TP = 0b10101010; // jeder 2. Port bekommt das umgekehrte Signal void setup() { DDRC = 0b11111111; // alle Analogports als Ausgang definieren // Timer 1 initialisieren noInterrupts(); // Interrupts deaktivieren TCCR1A = 0; TCCR1B = 0; TCNT1 = 0; OCR1A = 200; // Compare Match Register setzen(16MHz / 200 = 80kHz Rechteck -> 40kHz Vollwelle ) TCCR1B |= (1 << WGM12); // CTC mode TCCR1B |= (1 << CS10); // Prescaler auf 1 ==> kein prescaling TIMSK1 |= (1 << OCIE1A); // Compare Timer Interrupt einschalten interrupts(); // Interrupts aktivieren } ISR(TIMER1_COMPA_vect) { PORTC = TP; // den Wert TP an die Ausgänge senden TP = ~TP; // TP invertieren für den nächsten Durchlauf } void loop() { // hier bleibt nichts zu tun übrig :-( } |
Die Empfänger-US-Kapsel werde ich hoffentlich direkt ohne Verstärker an ein True-RMS-Multimeter im VAC-Modus hängen können. Bei meinem Interferenz-Experiment ebenfalls mit solchen US-Kapseln bekam ich etwa ein sehr starkes Signal mit Amplituden im Bereich um die 3V. Gut, hier ist die Distanz Sender-Empfänger um ein Vielfaches größer, aber ich habe auch die beiden Parabolspiegel, welche mir die Ultraschallwellen kollimieren und dann fokusieren. Mal schauen, sonst löte ich einen simplen Verstärker mit OPV…

Als Gitterkonstante werde ich so wie im Bild oben 1.5 cm probieren. Die Wellenlänge des Ultraschalls beträgt ja ca. 8.5 mm. Damit komme ich auf einen ersten Glanzwinkel von α = arcsin(λ/(2·d)) = arcsin(0.85/(2·1.5)) = ca. 16.5°. Das sollte eigentlich recht gut passen.
So, die auf Amazon bestellten Teile sind inzwischen eingetroffen und ich konnte mich an die Arbeit machen, das Atomgitter mit den Schaschlikspießen und Holzkugeln zu bauen. Dies ist eine regelrechte Strafarbeit, sind es doch 8³ = 512 Kugeln die ich einzeln aufbohren und dann mit Kleber auf den Spießen fixieren muss…






So, es ist vollbracht. Insgesamt 64 Holzstangen mit je 8 Holzkugeln. Dafür weisen meine Hände jetzt Blasen auf 😉

Als ich mit den Stäben fertig war, dachte ich das Schlimmste überstanden zu haben. Dem war aber nicht so. Der Zusammenbau des Gitters gestaltete sich dann um einiges anspruchsvoller. Denn ich musste die 64 Stäbe ja durch die Boden- und Deckplatte führen. Durch die Bodenplatte war ja einfach, aber dann die Stäbe auch an deren Oberseite durch die 64 Löcher zu stecken war ein absolutes Geduldspiel. Damit dies überhaupt klappen konnte längte ich die Stäbe zunächst stufenförmig ab.


Dann begann ich die Reihe mit den längsten Stäben einzufädeln. War dies geschehen, folgte die nächste Reihe mit den eine Spur kürzeren Stäben und so weiter. Das Problem bestand darin, dass sich die einzelnen Stäbe wieder aus ihren Löchern schoben, wenn man einen anderen Stab zu fixieren versuchte. Ein Stab rein, ein anderer wieder raus. Nach rund 20 mehr als anstrengenden Minuten war ich dann fertig und alle Stäbe durch die beiden Platten geführt. Noch einmal möchte ich dies aber nicht machen müssen…



Jetzt muss ich nur noch die Stäbe ablängen und sie dann auch mit der Deckplatte verleimen…
So, das Atomgitter ist fertig. Noch einmal tue ich mir eine solche Arbeit aber nicht mehr an 😉

Für die Ultraschallmodule lasse ich mit folgende Halterungen 3d-drucken:


Die Berechnung der zu erwartenden Glanzwinkel:

In der Zwischenzeit sind die ausgedruckten Halterungen angekommen:









Den Ultraschallsender steuere ich ja mit einem Arduino an. Den Empfänger möchte ich mit einem gewöhnlichen True-RMS-Multimeter auslesen. Dazu habe ich zum Testen 40 kHz-Signale bekannter Amplitude bzw. mit bekanntem RMS-Wert mit meinem Fluke-Multimeter gemessen:

Urms = 2.0 V:
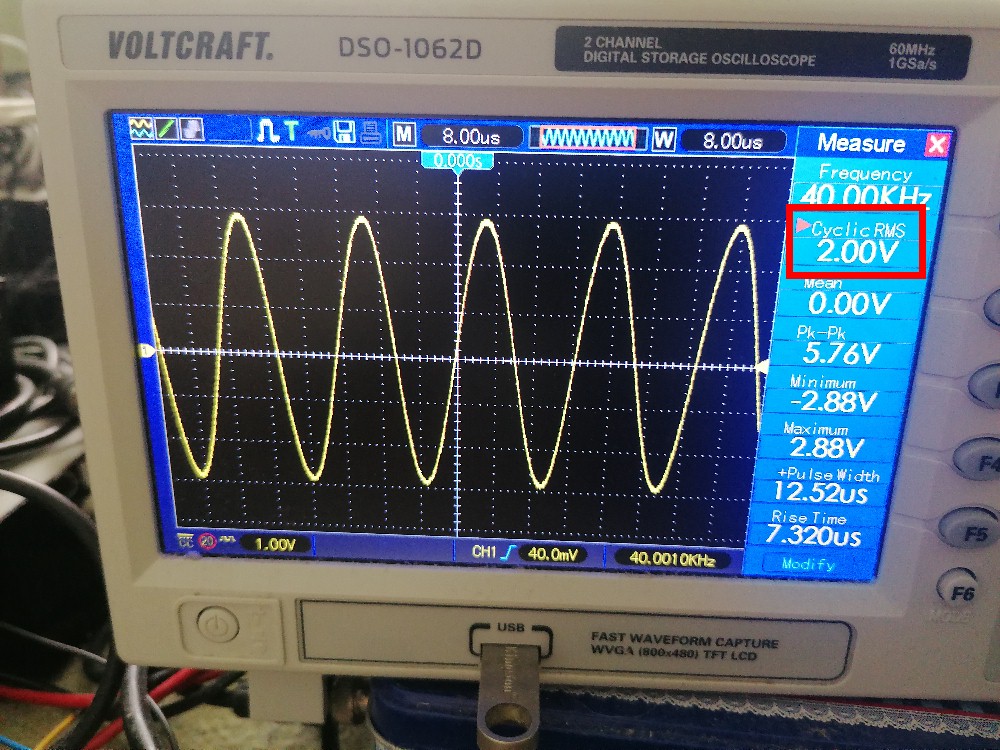
UMultimeter = 305 mV:

Urms = 1.0 V:
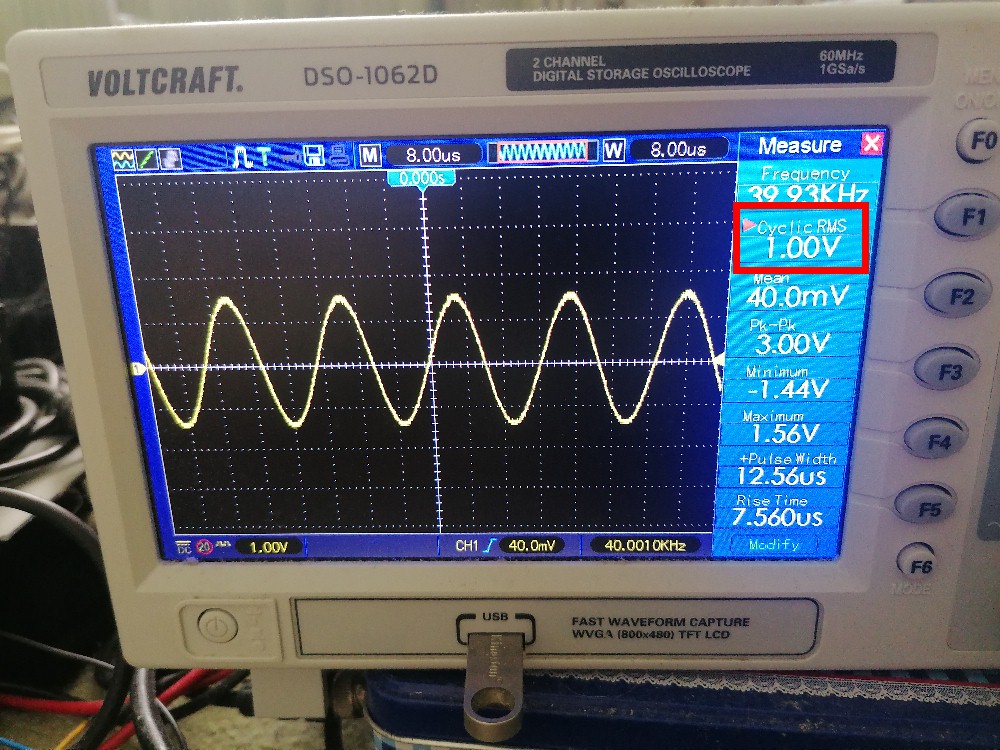
UMultimeter = 153.1 mV:

Urms = 0.5 V:
UMultimeter = 75.7 mV:

Das Multimeter zeigt war nicht den korrekten RMS-Wert an, aber die Ausgabe ist zumindest schön proportional zur Eingangsspannung. Von daher kann ich das Multimeter auch für das 40 kHz-Signal verwenden…
Für die einfache Einstellung der Sender- bzw. Empfängerposition habe ich mir eine halbkreisförmige Winkelskala ausgedruckt:
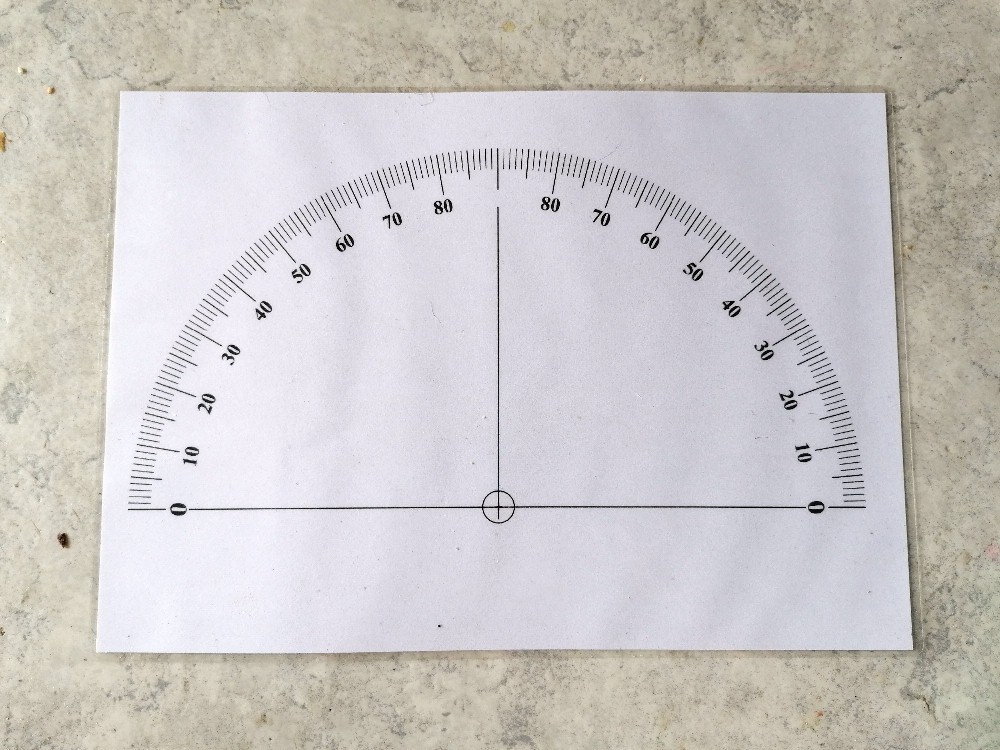
Die 3d-gedruckten Halterungen werde ich mittels einer M5 Gewindestange fixieren und drehbar lagern:



In der Zwischenzeit konnte ich das Experiment durchführen. Dazu habe ich eine M5-Schraube am Küchenboden als Achse für die beiden Ultraschallmodule festgeklebt:


Einfallswinkel = Ausfallswinkel = 60° = Glanzwinkel. Das Multimeter zeigt eine hohe Spannung an:

Einfallswinkel = Ausfallswinkel = 70° ≠ Glanzwinkel. Das Multimeter zeigt eine geringe Spannung an:

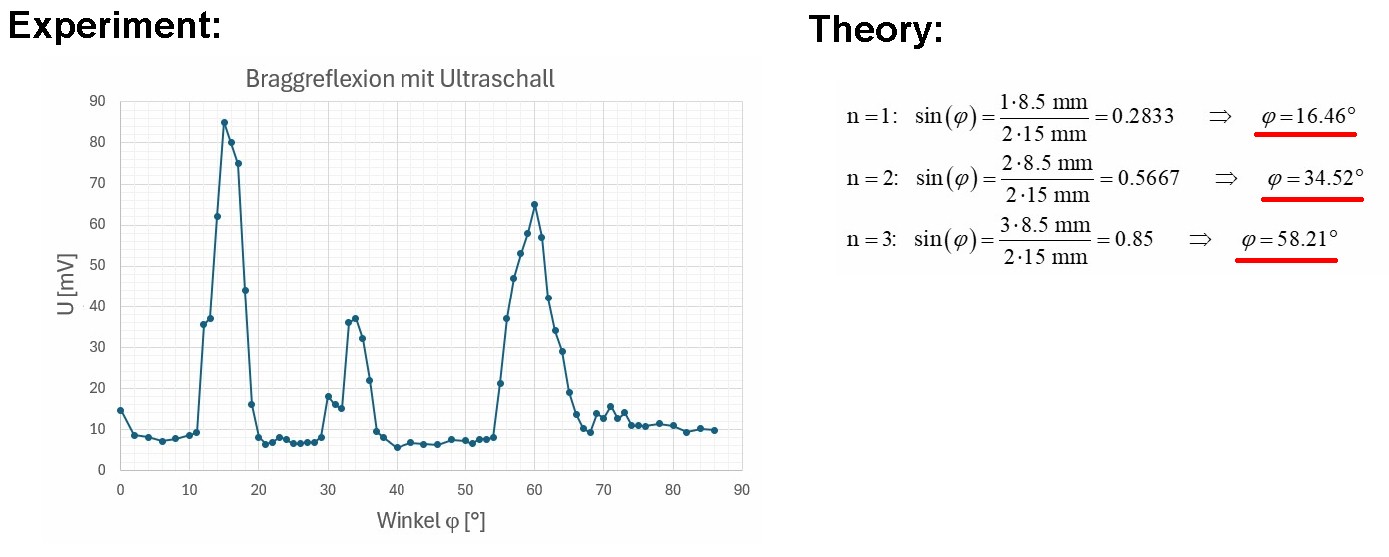
Hier nun die Messergebnisse:

Man erkennt wunderschön die Glanzwinkel bei ca. φ = 15°, 34° und 60°. Laut Theorie sollten sie bei 16.46°, 34.52° und 58.21° liegen. Besser hätte es nicht laufen können, Heureka 😉
Wie immer zum Abschluss das Youtube-Video:

