Es handelt sich bei der Boltzmannkonstanten zwar um eine ganz zentrale physikalische Konstante aus dem Bereich der Thermodynamik, aber sie besitzt trotzdem atomaren Charakter. Deshalb habe ich sie hier im Kapitel Atomphysik eingegliedert. Die Boltzmannkonstante ist nach dem österreichischen Physiker Ludwig Boltzmann (1844-1906) benannt.

Bildquelle: Wikipedia
Die Boltzmannkonstante stellt den Zusammenhang zwischen der Temperatur T und der Energie eines Teilchens her. Es gilt für die Energie eines einzelnen Freiheitsgrades:
EFG = 1/2 · kB · T
Liegt eine bestimmte Temperatur T vor, so besitzt jeder Freiheitsgrad des Teilchens/Moleküls die Energie EFG. Umgekehrt führt man Teilchen eine bestimmte Energie/Wärme zu und jeder Freiheitsgrad erhält die Energie EFG, so steigt die Temperatur um den Wert
ΔT = 2 · EFG / kB
Ein ideales Gas besitzt 3 Freiheitsgrade und zwar kinetische Energie in x-, y- und z-Richtung. Demnach besitzt ein ideales Gasteilchen bei der Temperatur T die Energie
Ekin,ideales Gas = 3/2 · kB · T
Die Temperatur T ist also ein Maß für die kinetische Energie der Teilchen.
Anhand obiger Erklärungen wird klar, dass bei einer bestimmten Temperatur T ein Teilchen mit mehr Freiheitsgraden auch eine größere Energie besitzt, denn es gilt ja Eges = f · 1/2 · kB · T.
Teilchen mit mehr Freiheitsgraden besitzen aber auch eine größere spezifische Wärmekapazität c. c ist direkt proportional zu f! Für die notwendige Energie um einen Körper mit der spezifischen Wärmekapazität c von T = 0 K auf die Temperatur T zu bringen gilt:
Q = c · m · T
In einem Körper mit einer größeren spezifischen Wärmekapazität (mehr Freiheitsgraden) steckt also bei gleicher Temperatur mehr Wärme/Energie.
Umgekehrt führt man einem Körper mit einer größeren Anzahl an Freiheitsgraden f (= höhere spezifische Wärmekapazität c) eine bestimmte Energie/Wärme zu, so bleibt für jeden Freiheitsgrad weniger Energie/Wärme übrig und die die erzielte Temperaturerhöhung
ΔT = (2 / f) · Qzu / kB
ist geringer. Dies ist aber auch anhand der Formel Q = c · m · ΔT ersichtlich. Ein Körper mit einer höheren spezifischen Wärmekapazität c ist schwerer zu erwärmen bzw. erwärmt sich bei gleichen, zugeführten Q weniger stark.
Wie kann man nun die Boltzmannkonstante experimentell bestimmen?
Variante 1: Shockleygleichung
Eine Diode sperrt ja bekanntlich bis zu einer Spannung von ca. 0.5 – 0.7 V. Darüber steigt der Strom aber sehr stark (exponentiell) an.
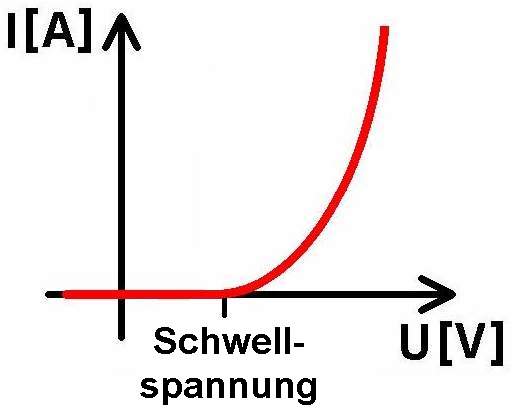
Die Shockleygleichung beschreibt den theoretischen Verlauf der Stromstärke I in Abhängigkeit von der Flussspannung U einer Diode.

Trägt man also den natürlichen Logarithmus der Stromstärke ln(I) durch die Diode in Abhängigkeit von der Flussspannung der Diode U auf, so erhält man eine Gerade mit dem Anstieg e / (ε · kB · T).

Der Schaltplan ist sehr simpel: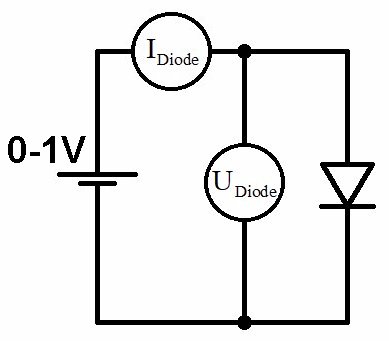





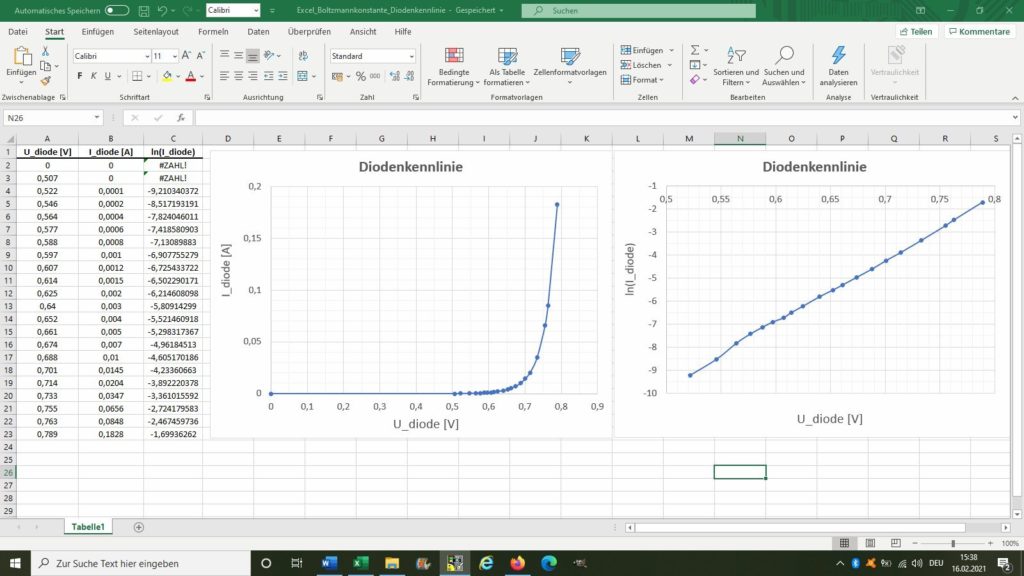


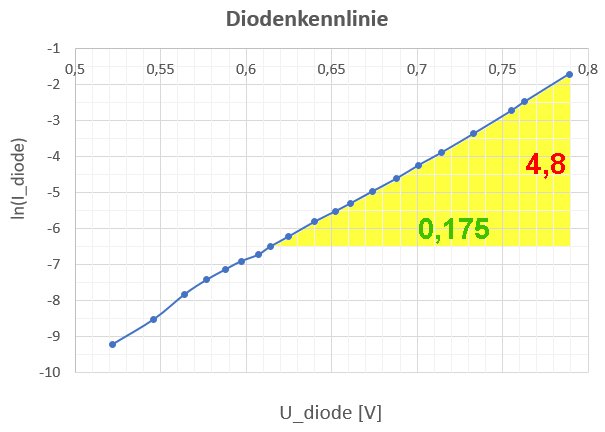
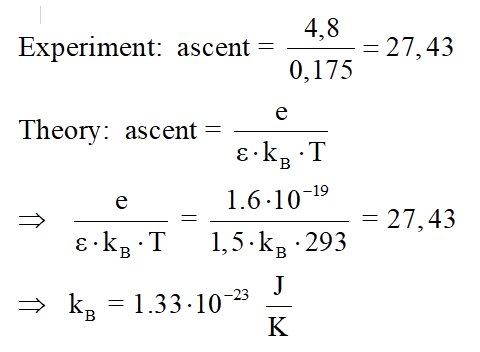
Der Sollwert für die Boltzmannkonstante liegt bei kB = 1,38 · 10^ –23 J/K. Somit ist die Abweichung des experimentell ermittelten Werts sehr gering.
Variante 2: Gasgesetz
Auch im Gasgesetz p · V = n · kB · T, welches die Größen Druck p, Volumen V, Teilchenanzahl n und Temperatur T miteinander verknüpft, kommt die Boltzmannkonstante kB vor.
Wenden wir das Gasgesetz konkret für die Verhältnisse von Luft auf Meereshöhe an, so können wir daraus die Boltzmannkonstante ermitteln.
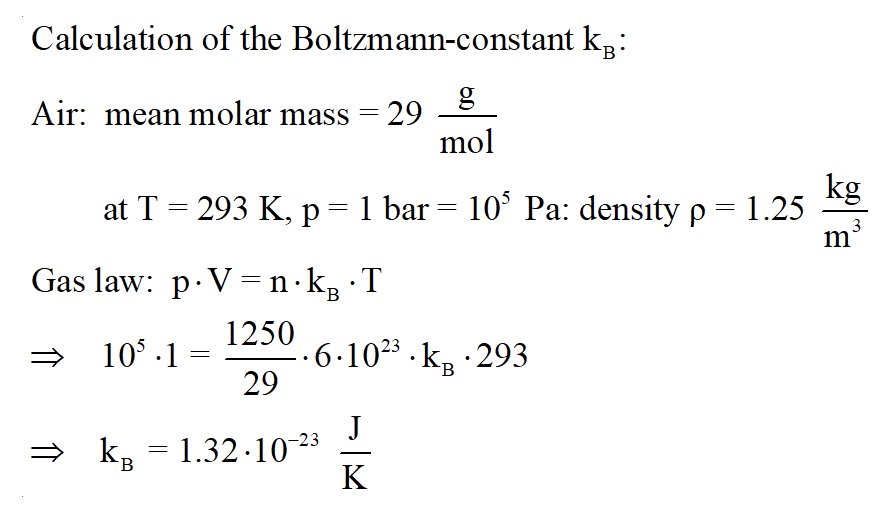
Auch dieses Ergebnis ist zufriedenstellend.

