
Bildquelle: Wikipedia
Führt man einem Körper (Festkörper, Flüssigkeit oder Gas) eine bestimmte Wärmeenergie Q zu, so steigt logischerweise dessen Temperatur. Die dazugehörige Formel lautet:


Welche anschauliche Bedeutung hat nun c? Die spezifische Wärmekpazität c ist genau Q, wenn m = 1 kg und ΔT = 1°C. c ist also die notwendige Wärmemenge, um 1 kg des Stoffs um 1°C zu erwärmen. Die spezifische Wärmekapazität von Wasser beträgt zum Beispiel 4155 J/kg·°C = 1 kcal/kg·°C.
Wie kann man die spezifische Wärmekapazität von einem Festkörper einfach bestimmen? Man erhitzt zunächst den Festkörper der Masse mMetall auf eine bekannte Temperatur, z.B. 100°C im kochenden Wasser. Danach gibt man den Körper in ein mit Wasser (Masse mWasser, Temperatur TWasser) gefülltes Glas. Dadurch steigt dessen Temperatur und es stellt sich eine Mischtemperatur TMisch ein.
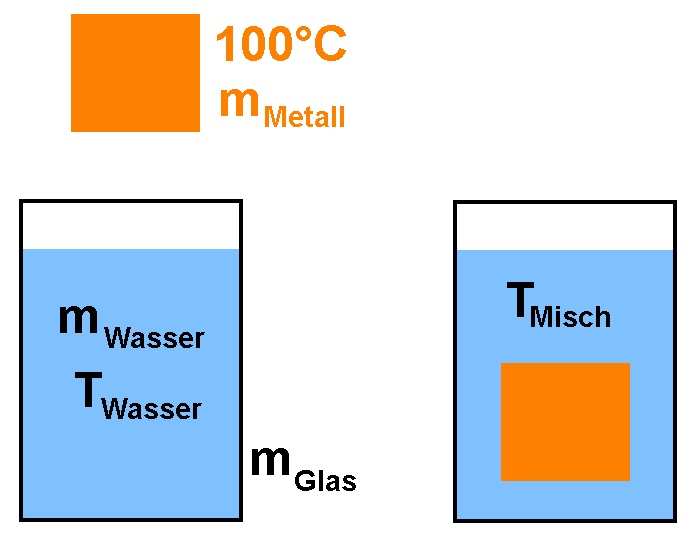
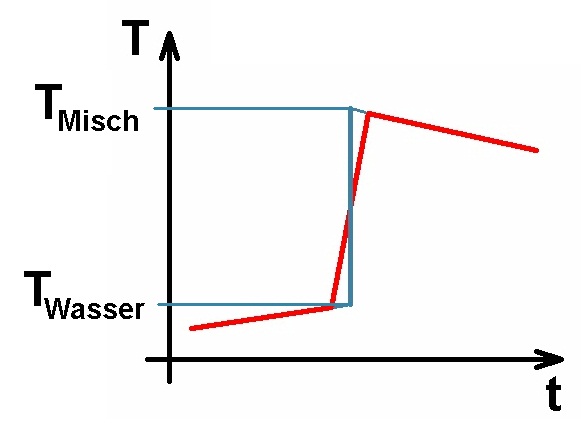
Die vom Metall abgegebene Wärmemenge Qab muss natürlich der dem Wasser und dem Glas zugeführten Wärmemenge Qzu entsprechen. Daraus lässt sich dann die unbekannte spezifische Wärmekapazität cMetall des Metalls bestimmen.

Was besagt aber nun die Regel von Dulong-Petit? Sie sagt aus, dass für Festkörper die molare spezifische Wärmekapazität, also die notwendige Wärmemenge, um 1 mol des Stoffs um 1°C zu erwärmen, genau der 3-fachen Gaskonstante R entspricht. Die Herleitung dieser Regel ist recht simpel. Ausgangspunkt ist der Zusammenhang zwischen der mittleren kinetischen Energie Ekin eines Teilchens pro Freiheitsgrad und der Temperatur T: Ekin = 1/2 · kB · T.

Die für diesen Versuch benötigten Metallwürfel aus Aluminium, Kupfer und Eisen habe ich auf Amazon entdeckt:








Das Experiment konnte ich heute erfolgreich durchführen. Die Erwärmung des Wassers (ca. 300 g) betrug zwischen 2-4°C. Die Erwärmung des Glasgefäßes wurde vernachlässigt. Die erhaltenen spezifischen Wärmekapazitäten liegen relativ nahe bei den Sollwerten und die molaren spezifischen Wärmekapazitäten in der Nähe des Sollwerts von 25 J/mol·°C, Heureka 😉






Hier zum Abschluss die drei Temperaturgraphen und die Berechnungen der molaren spezifischen Wärmekapazitäten:




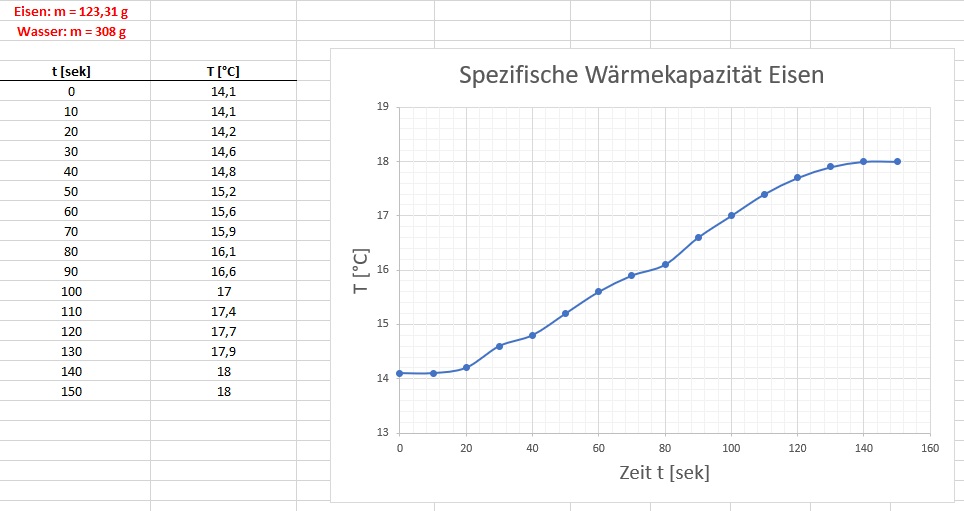

Wie man sieht, liegen die molaren spezifischen Wärmekapazitäten von Eisen, Kupfer und Aluminium nahe am Sollwert 3·R = 24.9 J/mol·°C:

Zum Schluss noch das Youtube-Video:

