Der Tunneleffekt ist ein quantenmechanisches Phänomen, welches klassisch nicht zu erklären ist. Nehmen wir zum Beispiel eine Hochschaubahn:
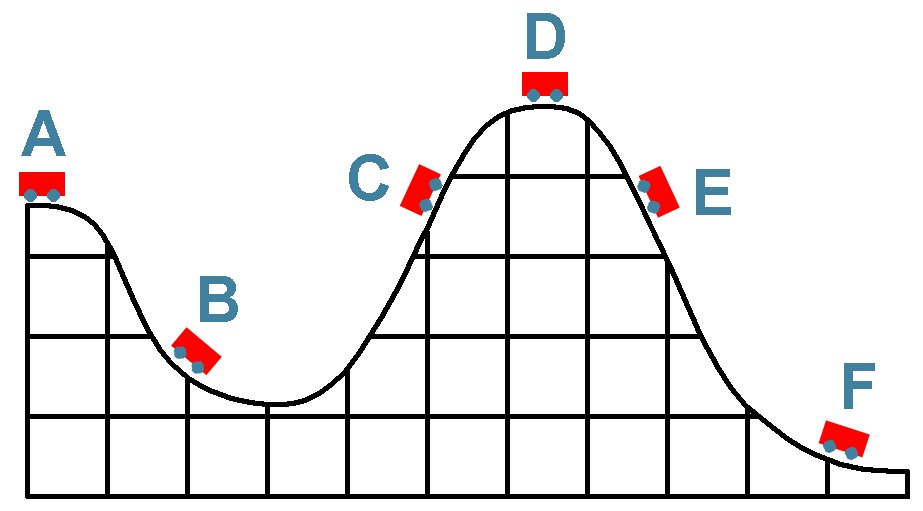
Der Wagen wird am Punkt A losgelassen. Er saust zu Beginn hinab und besitzt am Ort B aufgrund der Reduzierung seiner potentiellen Energie eine hohe kinetische Energie. Am Weg wieder hinauf wird seine kinetische Energie (Geschwindigkeit) nun kleiner, seine potentielle Energie steigt aber wieder. Klassisch betrachtet und ohne Reibung würde der Wagen am Ort C (gleiche Höhe wie Punkt A) zum Stillstand kommen. Er könnte niemals den Punkt D erreichen bzw. den Berg überwinden, da seine Gesamtenergie nicht für die zu hohe potentielle Energie im Punkt D ausreicht. Was passiert aber quantenmechanisch?
Der Wagen kann quantenmechanisch aber durch diese scheinbar unüberwindbare Energiebarriere von C nach E durchtunneln. Am Ort E angekommen nimmt er wieder in Richtung Ort F an Fahrt auf. Der Tunneleffekt erklärt also, wie quantenmechanische Objekte (zum Beispiel Elektronen) energetische Hindernisse überwinden, obwohl die Teilchenenergie eigentlich dazu nicht ausreichen dürfte.
Ausgangspunkt quantenmechanischer Berechnungen ist die sog. Schrödingergleichung. Dabei handelt es sich um eine Differentialgleichung mit der gesuchten Wellenfunktion ψ(r,t) bzw. ψ(r).

Nehmen wir für das Potential V(x) folgende Potentialbarriere 
Klassisch betrachtet könnte ein Teilchen mit der Energie E < V0 diese Potentialbarriere nicht überwinden und sich im Bereich III nach rechts weiter fortbewegen.
Um die Schrödingergleichung zu lösen, setzt man für die Bereiche I und III mit V(x) = 0 folgende Wellenfunktion ψ(x) an:

Setzt man ψ(x) und ψ”(x) in die Schrödingergleichung ein, erhält man folgende Lösungsfunktion für die Bereiche I und III:

Für den Bereich II mit V(x) = V0 setzt man für die Wellenfunktion ψ(x) wiefolgt an:
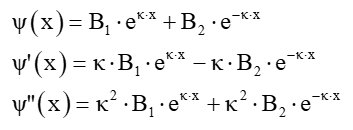
Dies liefert eingesetzt in die Schrödingergleichung folgendes Ergebnis für die Wellenfunktion im Bereich II:

Insgesamt lautet die Wellenfunktion ψ(x) also:


Wie man erkennen kann, nimmt die Wellenfunktion ψ(x) im Bereich II zwar exponentiell ab, sie ist aber am rechten Ende der Potentialbarriere bei x = a nicht vollends verschwunden. Graphisch dargestellt gilt also für die Wellenfunktion folgender Verlauf:
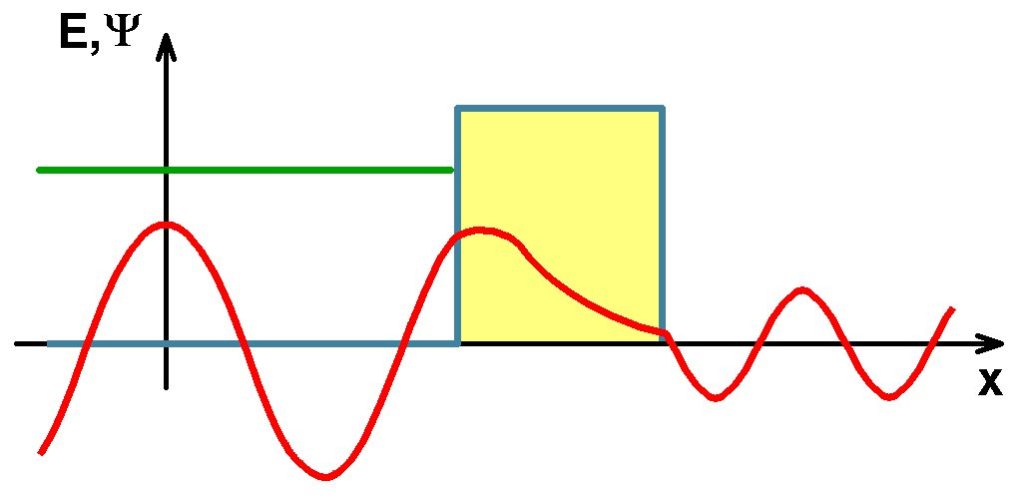
Die Wellenfunktion nimmt zwar im Bereich der Potentialbarriere exponentiell ab, sprich die Aufenthaltswahrscheinlichkeit wird immer geringer, aber ist die Potentialbarriere nicht zu breit, so besteht für das Teilchen eine bestimmte Wahrscheinlichkeit, diese Barriere zu durchtunneln und im Bereich III noch existent/detektierbar zu sein. Für die Tunnelwahrscheinlichkeit T ergibt sich schlussendlich der Ausdruck

Dieser Tunneleffekt wird gezielt beim sog. Rastertunnelmikroskop (RTM oder engl. scanning tunneling microscope, kurz STM) ausgenutzt. Bei diesem Mikroskop fährt man mit einem sehr spitzen Draht (in meinem Fall aus Platin) die zu untersuchende Oberfläche rasterförmig ab, ohne dass der Draht diese berührt. Klassisch betrachtet kann kein Elektron vom Draht zur Oberfläche gelangen. Quantenmechanisch tunneln nun aber Elektronen vom Draht zur Oberfläche und es fließt ein sehr geringer Tunnelstrom. Dieser ist natürlich abhängig vom Abstand des Drahts zur Oberfläche. Die Position des Drahts ist mittels Piezoelementen regelbar. In x- und y-Richtung wird der Draht über die Oberfläche geführt/gescannt. In z-Richtung wird der Draht nun so positioniert, dass immer der gleiche Tunnelstrom fließt. Gleicher Tunnelstrom bedeutet aber in etwa gleicher Abstand Drahtspitze-Oberfläche. Gelangt die Drahtspitze etwa zu einem Oberflächenhindernis, so muss die z-Komponente des Drahts abgeändert werden und dieser weicht dem Hindernis nach oben aus. Bei einer Mulde und demnach größeren Abstand Drahtspitze-Oberfläche würde der Tunnelstrom abnehmen. Um diesen dennoch konstant zu halten, muss der z-Piezo gedehnt werden, damit sich die Spitze wieder der Oberfläche auf den Sollabstand nähert. Die am z-Piezo anliegende Spannung ist also ein Maß für die jeweilige Oberflächenstruktur.

Kennt man nun das Steuersignal des z-Piezos in Abhängigkeit von den x- und y-Steuersignalen, so lässt sich auf diese Weise die (atomare) Struktur der untersuchten Oberfläche abbilden. Wandelt man die notwendige Steuerspannung des z-Piezos in Abhängigkeit von der Drahtposition (x,y) in einen Grauwert um, so erhält man ein Abbild der Oberfläche.

Abbildung: Atomare Auflösung von HOPG (hochorientierter, pyrolitischer Graphit: ein Graphitkristall, der sehr regelmässige und glatte Spaltflächen hat). Aufnahme mit einem STM-Nachbau von Sven Ullrich
Kann man nun ein solches Tunnelmikroskop als Amateur bauen? Die Antwort lautet “Ja”. Mein Rastertunnelmikroskop basiert auf einem Projekt der deutschen Universität Münster. Diese stellte im Jahr 2004 den kompletten Bau eines STM vor. Im Laufe der Jahre besorgte ich mir Teil für Teil zur Umsetzung dieses Projekts. So kam auch die für den Betrieb notwendige PC-Steuerkarte PC20TR der deutschen Firma BMC Messsysteme GmbH in meinen Besitz. Diese gibt über 2 steuerbare, analoge Ausgänge die Spannungen für den x- und y-Piezo aus und liest zeitgleich über 2 analoge Eingänge den von der Steuerelektronik konstant gehaltenen Tunnelstrom I und die Spannung des z-Piezos ein. Damit erzeugt die Software dann ein Abbild der untersuchten Oberfläche.

Da für den Betrieb des Tunnelmikroskops also immer ein PC mit dem veralteten ISA-Kartenslot vonnöten ist, schaute ich mich nach einer kompakteren Lösung um und wurde beim Arduino fündig. Anfang 2016 begann ich damit, das STM auf Arduino-Betrieb umzurüsten. Nun ist kein PC mehr zum Betrieb des Tunnelmikroskops notwendig. Das Bild wird direkt auf einem 320×480 pixel Display ausgegeben. Den Tunnelstrom bzw. die Spannung am z-Piezo kann man als bargraph auf einem 16×2 Display überwachen.
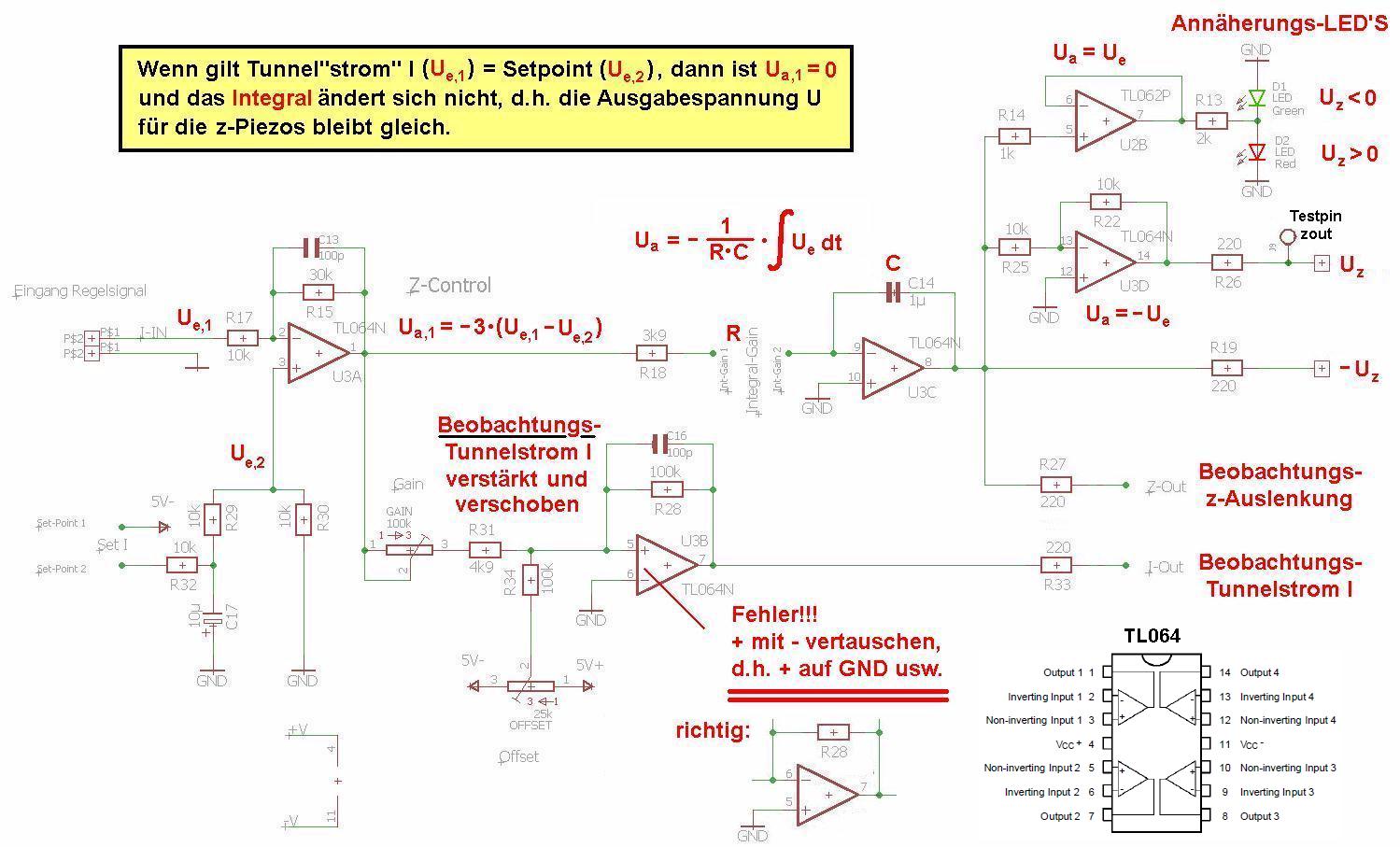
Die beiden Steuersignale für den x- und y-Piezo mit den Spannungsbereichen [-10V,+10V] werden mittels DAC MCP4922 und nachfolgendem Operationsverstärker (LM358) erzeugt. Die Eingangssignale/spannungen des z-Piezos und des Tunnelstroms werden ebenfalls mittels Operationsverstärker von [-10V,+10V] nach für den Arduino kompatible [0,+5V] umgewandelt.
ACHTUNG: Bei der Platine für die Steuerung/Regelung hat sich beim IC TL064N (U3B im Schaltplan) ein Fehler eingeschlichen! Pin 5 (nicht invertierender Eingang) muss eigentlich mit GND verbunden sein und Pin 6 (invertierender Eingang) mit den Widerständen R34, R31 und R28 bzw. dem Kondensator C16.
Hier nun die Bilder meines Rastertunnelmikroskops inklusive der Steuer/Regelungsbox:


















Folgende Bilder dokumentieren die Veränderungen beim Umbau auf Arduino-Betrieb:



















Zum Abschluss eine noch mit dem alten Setup (mit PC und ohne Arduino) erhaltene Aufnahme einer Goldoberfläche. Ergebnisse mit dem neuen Arduino-Setup sind noch ausständig!

Arduino-Code:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299 300 301 302 303 304 305 306 307 308 309 310 311 312 313 314 315 316 317 318 319 320 321 322 323 324 325 326 327 328 329 330 331 332 333 334 335 336 337 338 339 340 341 342 343 344 345 346 347 348 349 350 351 352 353 354 355 356 357 358 359 360 361 |
// ================================================== // ============ RASTERTUNNELMIKROSKOP =============== // ================================================== #include "AH_MCP4922.h" #include <LiquidCrystal_I2C.h> #include <Wire.h> #include <UTFT.h> // Declare which fonts we will be using extern uint8_t SmallFont[]; UTFT myGLCD(CTE32HR,38,39,40,41); LiquidCrystal_I2C lcd(0x27,16,2); // set the LCD address to 0x27 for a 16 chars and 2 line display ACHTUNG: Adresse kann auch 0x3F sein !!! // Anschlüsse: // GND - GND // VCC - 5V // SDA - D20 beim Mega ANALOG Pin 4 beim Uno // SCL - D21 beim Mega ANALOG pin 5 beim Uno double Prozent = 100.0; double a; unsigned char b; unsigned int Rest; // custom characters // ================= byte p1[8] = {B10000,B10000,B10000,B10000,B10000,B10000,B10000,B10000}; byte p2[8] = {B11000,B11000,B11000,B11000,B11000,B11000,B11000,B11000}; byte p3[8] = {B11100,B11100,B11100,B11100,B11100,B11100,B11100,B11100}; byte p4[8] = {B11110,B11110,B11110,B11110,B11110,B11110,B11110,B11110}; byte p5[8] = {B11111,B11111,B11111,B11111,B11111,B11111,B11111,B11111}; //define AnalogOutput (MOSI_pin, SCK_pin, CS_pin, DAC_x, GAIN) AH_MCP4922 AnalogOutput1(11,13,12,LOW,HIGH); // define AnalogOutput1 for UNO_board, select DAC_A, Gain=1x AH_MCP4922 AnalogOutput2(11,13,12,HIGH,HIGH); // define AnalogOutput2 for UNO_board, select DAC_B, Gain=1x // Arduino-Pin 11 verbunden mit IC-Pin 5, Arduino-Pin 12 verbunden mit IC-Pin 3, Arduino-Pin 13 verbunden mit IC-Pin 4 /******************************** * | MEGA | UNO * * -------------------------- * * SCK_pin | 52 | 13 * * MOSI_pin | 51 | 11 * * CS_pin | 53 | 12 * ********************************* * DAC=LOW => DAC_A select * * DAC=HIGH => DAC_B select * * * * GAIN=LOW => 2x gain select * * GAIN=HIGH => 1x gain select * ********************************/ int intputPin_z = A0; // Deklaration des input-pin für z_piezo int inputPin_i = A1; // Deklaration des input-pin für Tunnelstrom int startPin = 2; // Deklaration des Start-Pins int buttonState; // Variable für Starttaste int x,y; // x- und y-Output für x- und y-piezo int z_piezo = 0; // Variable für den Spannungswert des z-piezos int tunnelstrom = 0; // Variable für den Tunnelstrom int value; // Grauwert // =========================== // ========== SETUP ========== // =========================== void setup() { Serial.begin(115200); // Init serial interface pinMode(startPin, INPUT); buttonState = HIGH; // Starttaste noch nicht gedrückt lcd.init(); // initialize the lcd lcd.backlight(); lcd.setCursor(0,0); lcd.print("Rastertunnel-"); lcd.setCursor(0,1); lcd.print("mikroskop"); delay(3000); lcd.setCursor(0,0); lcd.print("Annaeherungs-"); lcd.setCursor(0,1); lcd.print("modus "); delay(3000); lcd.setCursor(0,0); lcd.print("When ready "); lcd.setCursor(0,1); lcd.print("push button..."); delay(3000); lcd.createChar(0, p1); lcd.createChar(1, p2); lcd.createChar(2, p3); lcd.createChar(3, p4); lcd.createChar(4, p5); // Setup the LCD myGLCD.InitLCD(); myGLCD.setFont(SmallFont); myGLCD.clrScr(); myGLCD.setColor(255, 255, 0); myGLCD.fillRect(0, 0, 479, 13); myGLCD.setColor(0, 0, 0); myGLCD.setBackColor(255, 255, 0); myGLCD.print("Rastertunnelmikroskop - stoppi", CENTER, 1); } // =========================== // ====== HAUPTSCHLEIFE ====== // =========================== void loop() { AnalogOutput1.setValue(0); AnalogOutput2.setValue(0); buttonState = HIGH; // =================================================== // ==== Annäherungsphase vor Beginn der Rasterung ==== // ========= Startknopf noch nicht gedrückt ========== // =================================================== while(buttonState == HIGH) // Starttaste noch nicht gedrückt { z_piezo = analogRead(intputPin_z); // Einlesen der Spannung des z-Piezos tunnelstrom = analogRead(inputPin_i); // Einlesen des Tunnelstroms Anzeige(); // Unterprogramm zur graphischen Darstellung des Tunnelstroms und des z-Piezos buttonState = digitalRead(startPin); } // ============================================ // ============ Startknopf gedrückt =========== // ========= Beginn der x/y-Rasterung ========= // ============================================ delay(1000); for (y = 0; y < 76; y++) { AnalogOutput2.setValue(y * 34); // Ausgabe des y-Werts; Maximum = 4095 == 5V! // Rasterung nach rechts // ===================== for (x = 0; x < 120; x++) { AnalogOutput1.setValue(x * 34); // Ausgabe des y-Werts; Maximum = 4095 == 5V! delay(5); z_piezo = analogRead(intputPin_z); // Einlesen der Spannung des z-Piezos tunnelstrom = analogRead(inputPin_i); // Einlesen des Tunnelstroms Anzeige(); // Unterprogramm zur graphischen Darstellung des Tunnelstroms und des z-Piezos value = z_piezo; value = map(value,0,1023,0,255); myGLCD.setColor(255 - value,255 - value,255 - value); // großer z-Wert (positiv) bedeutet Mulde -> dunkel; kleiner z-Wert (negativ) bedeutet Hügel -> hell myGLCD.fillRect(x * 4, 15 + y * 4, x * 4 + 3, 15 + y * 4 + 3); } y++; AnalogOutput2.setValue(y * 34); // set voltage for AnalogOutput1 = IC-pin 10 // Rasterung nach links // ==================== for (x = 119; x >= 0; x--) { AnalogOutput1.setValue(x * 34); // set volateg for AnalogOutput2 = IC-pin 14 delay(5); z_piezo = analogRead(intputPin_z); // Einlesen der Spannung des z-Piezos tunnelstrom = analogRead(inputPin_i); // Einlesen des Tunnelstroms Anzeige(); // Unterprogramm zur graphischen Darstellung des Tunnelstroms und des z-Piezos value = z_piezo; value = map(value,0,1023,0,255); myGLCD.setColor(255 - value,255 - value,255 - value); // großer z-Wert (positiv) bedeutet Mulde -> dunkel; kleiner z-Wert (negativ) bedeutet Hügel -> hell myGLCD.fillRect(x * 4, 15 + y * 4, x * 4 + 3, 15 + y * 4 + 3); } } // Langsame Fahrt in die Ausgangsposition x = y = 0 // ================================================ AnalogOutput1.setValue(0); for (y = 75; y >= 0; y--) { AnalogOutput2.setValue(y * 34); delay(20); } } // ============================================================= // == Unterprogramm zur Anzeige des Tunnelstroms und z-Piezos == // ============================================================= void Anzeige() { // ============================== // Zeichnen des z_piezo-bargraphs // ============================== lcd.setCursor(0,0); Prozent = (z_piezo / 1023.0) * 100.0; // Umrechnen in % a = (16.0 / 100) * Prozent; // Ermittlung, bis zu welchem Rechteck der bargraph geht (z.B. 3.7; maximal bis zum 16-ten) // Zeichnen der vollen Rechtecke if (a >= 1) { for (int i = 1;i < a;i++) { lcd.write(4); // Ausfüllen mit vollen Rechtecken (entspricht character 4) b = i; } a = a - b; // verbleibender Rechtecksrest in Teilen eines ganzen Rechtecks, z.B. 0.7 } Rest = a * 5; // verbleibende Breite (minimal 0, maximal 5) des Rechtecksrests, z.B. 3.5 // drawing character's colums switch(Rest) { case 0: break; case 1: lcd.print((char)0); break; case 2: lcd.write(1); break; case 3: lcd.write(2); break; case 4: lcd.write(3); break; } // Ausfüllen des rechts freibleibenden Rests mit Leerzeichen for (int i = 0;i < (16.0 - b);i++) { lcd.print(" "); } // ================================== // Zeichnen des tunnelstrom-bargraphs // ================================== lcd.setCursor(0,1); Prozent = (tunnelstrom / 1023.0) * 100.0; // Umrechnen in % a = (16.0 / 100) * Prozent; // Ermittlung, bis zu welchem Rechteck der bargraph geht (z.B. 3.7; maximal bis zum 16-ten) // Zeichnen der vollen Rechtecke if (a >= 1) { for (int i = 1;i < a;i++) { lcd.write(4); // Ausfüllen mit vollen Rechtecken (entspricht character 4) b = i; } a = a - b; // verbleibender Rechtecksrest in Teilen eines ganzen Rechtecks, z.B. 0.7 } Rest = a * 5; // verbleibende Breite (minimal 0, maximal 5) des Rechtecksrests, z.B. 3.5 // drawing character's colums switch(Rest) { case 0: break; case 1: lcd.print((char)0); break; case 2: lcd.write(1); break; case 3: lcd.write(2); break; case 4: lcd.write(3); break; } // Ausfüllen des rechts freibleibenden Rests mit Leerzeichen for (int i = 0;i < (16.0 - b);i++) { lcd.print(" "); } } |

