Mit einem sog. ballistischen Pendel lässt sich die Geschwindigkeit von Projektilen/Pfeilen bestimmen. Die Basis für die Berechnung bilden der Impulserhaltungs- und Energieerhaltungssatz. Diese besagen, dass der Gesamtimpuls vor/nach dem Stoß konstant ist bzw. die Energie vor/nach dem Stoß gleich bleibt. Wie wir sehen werden, führt der Einschlag des Pfeiles zu „Energieverlusten“, sodass wir für eine korrekte Berechnung der Pfeilgeschwindigkeit auf den Impulserhaltungssatz zugreifen müssen.

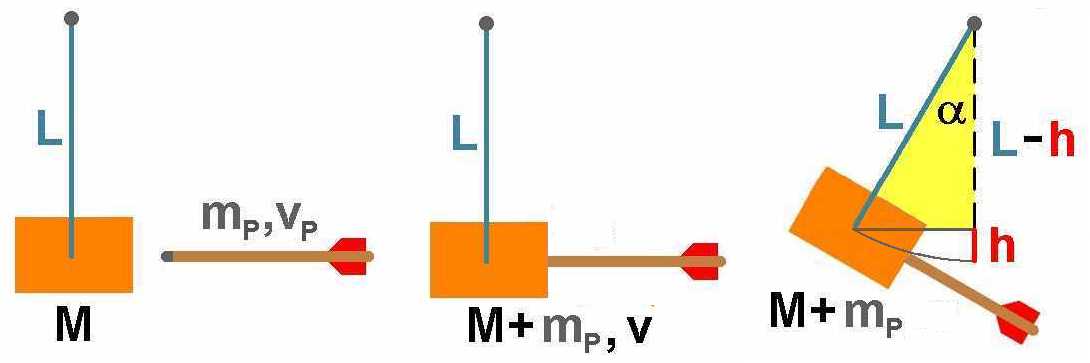
Wie sieht die Physik hinter dem ballistischen Pendel aus? Ein Pfeil mit der Masse m_P werde mit einer Geschwindigkeit v_P auf ein Ziel (konkret ein mit Holz beschwerter Schaumstoffkörper) mit der Masse M geschossen, welches an einem Seil aufgehängt ist. Der Pfeil bleibt im Ziel stecken und das Pendel vollführt dadurch Schwingungen mit einem maximalen Auslenkungswinkel α.

Über den Auslenkwinkel α lässt sich der Höhengewinn h wiefolgt berechnen:  h = L – L · cos(α) = L · [1 – cos(α)].

Der Energieerhaltungssatz besagt nun, dass während der Auslenkung des Pendels bei Vernachlässigung von Reibung (z.B. in der Aufhängung oder durch den Luftwiderstand) die Gesamtenergie E = Summe der kinetischen Energie E_kin + potentielle Energie E_pot konstant bleibt. Zu Beginn der Auslenkung direkt nach dem Eindringen des Pfeils verfügt das Ziel nur über kinetische Energie (Bewegungsenergie), welche dann mit zunehmender Auslenkung in potentielle Energie (Energie der Lage) umgewandelt wird.

Setzt man in die Formel den Höhengewinn h ein, so lässt sich die Geschwindigkeit v des Ziels (Schaumstoff + darin steckender Pfeil) berechnen.

Wie gelangt man nun aber zur Geschwindigkeit des Pfeils? Hierzu bedienen wir uns des Impulserhaltungssatzes:

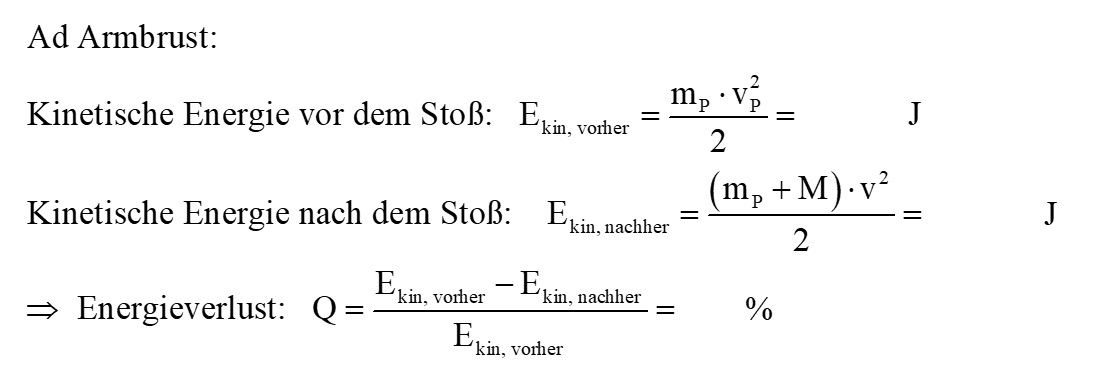
Jetzt könnte man natürlich auch auf die Idee kommen, die Pfeilgeschwindigkeit über die kinetischen Energien vor und nach dem Stoß zu berechnen. Hier müsste man wiefolgt ansetzen:

Wie man erkennen kann, unterscheiden sich beide Formeln zur Berechnung der Pfeilgeschwindigkeit v_P voneinander. Einmal befindet sich der Ausdruck mit den Massen unter einer Wurzel, im ersten Fall fehlt die Wurzel.

Welche Methode ist aber nun richtig? Betrachten wir hierzu einmal den Fall eines komplett inelastischen Stoßes zweier gleicher Münzen mit der Masse m:

Durch die Knetmasse wird garantiert, dass die beiden Münzen nach der Kollision beisammen kleben bleiben. Wollen wir die Geschwindigkeit v‘ nach dem Stoß ermitteln, bedienen wir uns wieder des Impulserhaltungssatzes:

Man erkennt, dass der Stoß zu einem Energieverlust konkret um 50% der kinetischen Energie vor dem Stoß geführt hat. Genau aus diesem Grund dürfen wir also zur Berechnung der Pfeilgeschwindigkeit NICHT die kinetischen Energien des Ziels bzw. des Pfeils gleichsetzen! Zur Berechnung der Pfeilgeschwindigkeit müssen wir die Formel basierend auf der Impulserhaltung heranziehen, welche gelautet hat:

Würden wir die kinetischen Energien gleichsetzen, so hätten wir durch unberücksichtigte Verluste (Reibung, Wärme bzw. Verformung) eine zu geringe kinetische Energie des Pfeils erhalten und damit auch eine zu geringe Pfeilgeschwindigkeit!

Ballistische Pendel können im Schulmittelhandel zum Beispiel bei Conatex erworben werden: https://www.conatex.com/physik-lehrmittel/mechanik/kraefte-statik-dynamik/wurfgeraet-und-ballistisches-pendel/ballistisches-pendel.html

Ich wählte den Selbstbau. Daher habe ich mir für dieses Experiment eine 50 lbs Armbrust gekauft:

Als Ziel verwende ich einen Block aus Styrodurplatten, welchen ich mit UHU POR zusammengeklebt habe:

Eine spannende Überlegung zum total inelastischen Stoß:

Das heißt also, egal ob das Projektil spitz oder stumpf ist, ob es leicht verformbar ist oder nicht, ob es tief eindringt ins Pendel oder nicht, bei gleicher Projektilmasse, Projektilgeschwindigkeit und Pendelmasse ist die Summe aus erzeugter Wärme Q + geleisteter Verformungsarbeit W beim total inelastischen Stoß IMMER gleich. Wird daher zum Beispiel mehr Wärme erzeugt, muss die Verformungsarbeit entsprechend geringer gewesen sein und vice versa. Dies ist auf den ersten Blick nicht gerade einleuchtend. Aber so ist die Physik auch, je mehr man sich mit ihr beschäftigt und je tiefer man gräbt, umso komplexer und verästelter wird sie. Das liebe ich an der Physik bzw. hasse ich 😉

Das Experiment mit der Armbrust ist noch ausständig, da ich zur Durchführung inkl. Filmen eine zweite Person benötige. Wenn ich es durchgeführt habe, berichte ich hier davon…

 

---

In der Zwischenzeit habe ich die Geschwindigkeit meiner Luftdruckpistole mittels ballistischen Pendel in meiner Wohnung durchgeführt. Die Pistole habe ich vor vielen Jahren für die Physikolympiade bzw. das Physiklabor angeschafft und wird durch Knicken geladen. Somit erspare ich mir teure CO2-Patronen.

Auf der Verpackung ist die Projektilgeschwindigkeit mit v_P = 100 m/s angegeben, mal schauen wie nahe ich diesem Wert mit meinem Experiment komme:

Der Pendelkörper für die Armbrust ist viel zu schwer für die kleinen Bleigeschoße, daher habe ich mir schnell einen zweiten wieder aus Styrodur gebastelt:

Die Masse M beträgt genau 30.98 g:

Die Bleigeschoße sind mit 0.51 g angegeben, ich habe aber zur Sicherheit 10 Stück abgewogen und komme auf eine Masse m_P = 0.516 g:

Das Pendel besitzt eine Länge vom Aufhängepunkt bis zum Schwerpunkt der Masse M von L = 66 cm:

 

Die Videoauswertung erfolgt mit der Software „Tracker“:

Ich komme auf einen maximalen Auslenkungswinkel von 20.8°:

Mit diesem Wert kann dann die Projektilgeschwindigkeit zu v_P = 56.1 m/s bestimmt werden. Dies ist natürlich deutlich zu niedrig. Der Grund liegt darin, dass beim Pendel doch eine gewisse Energie auch in die Rotation des Pendelkörpers geht. Zudem besitzt das Pendel durch den Faden keine starre Aufhängung und der Pendelkörper eilt dem Faden zum Teil voraus bzw. hinterher. Besser wäre es wohl gewesen, wenn ich eine dünne Metallleiste anstelle des Fadens genommen hätte…

Die Berechnung der Geschwindigkeit über den Auslenkwinkel des Pendels ist also sehr ungenau. Daher habe ich die Geschwindigkeit des Pendelkörpers mittels Videoanalyse ermittelt und komme bei Verwendung des Smartphone-Videos mit 30 fps auf eine Geschwindigkeit v = 1.139 m/s. Mittels Auslenkwinkel waren es nur 0.919 m/s (siehe oben).

Der höhere Wert für v liefert eine Projektilgeschwindigkeit v_P = 69.5 m/s. Schon besser aber wohl noch immer deutlich zu wenig…

Deshalb habe ich zum Schluss noch die Geschwindigkeit v des Pendelkörpers im High-Speed-Video mit 420 fps bestimmt mit dem Ergebnis v = 1.756 m/s:

Setze ich diesen Wert in die Impulsgleichung, so erhalte ich eine Projektilgeschwindigkeit v_P = 107.2 m/s. Dieser Wert liegt nun recht nahe am Sollwert von v = 100 m/s.

Die kinetische Energie des Projektils beträgt bei dieser Geschwindigkeit fast 3 J, die kinetische Energie des Pendelkörpers nach dem Beschuß allerdings nur bescheidene 0.049 J. Demnach gehen konkret beim total inelastischen Stoß 98.35 % der kinetischen Energie verloren, beachtlich.

Daher wäre es komplett falsch, bei der Berechnung von v_P die kinetische Energie des Pendelkörpers mit jener des Projektils gleichzusetzen. Man würde eine massiv zu geringe Projektilgeschwindigkeit erhalten!