
Werden Drähte unterschiedlichen Materials miteinander verbunden und die beiden Kontaktstellen auf verschiedene Temperaturen gebracht, so misst man zwischen den Drahtenden eine Spannung, die sog. Thermospannung.
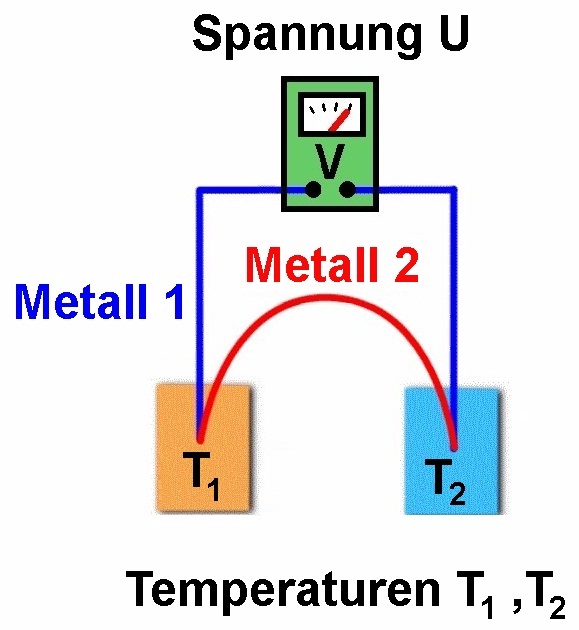
Ursache dieser elektrischen Spannung ist der sog. Seebeck-Effekt benannt nach dem Physiker Thomas Johann Seebeck (1770 – 1831). Diese Thermospannung hängt einerseits von den beiden Materialien und andererseits von der Temperaturdifferenz ΔT ab. Wählt man ein Material als Norm, in diesem Fall Platin, so kann man eine sog. thermoelektrische Spannungsreihe erstellen und den sog. Seebeck-Koeffizient angeben. Dieser besitzt für jedes Element die Einheit µV/K = µV/°C. Befinden sich zwei Materialien in der Spannungsreihe weit voneinander entfernt, so ist die zu messende Thermospannung pro °C Temperaturdifferenz groß und vice versa.
Die Umkehrung des Seebeck-Effekts ist der sog. Peltier-Effekt. Legt man an die Metalldrähte eine elektrische Spannung an, so erzielt man dadurch einen Temperaturunterschied der beiden Kontaktstellen.

Quelle: Wikipedia

Quelle: Wikipedia
In diesem Versuch möchte ich die Seebeck-Koeffizienten für verschiedene Materialien experimentell ermitteln. Die Durchführung ist denkbar einfach: Man verknüft die beiden unterschiedlichen Drähte miteinander und hält eine Kontaktstelle in einen Wasserkocher, die andere an der Luft. Dann schaltet man den Wasserkocher ein und bestimmt die Thermospannung in Abhängigkeit von der Wassertemperatur. Da die Thermospannungen sehr gering sind, benötigt man ein sehr sensibles Voltmeter. In meinem Fall kommt mein µV-Meter (https://stoppi-homemade-physics.de/mikrovoltmeter/) zum Einsatz. Dieses besitzt eine Verstärkung von 1000. Wird also eine Spannung von 1 mV abgezeigt, beträgt die Spannung 1 µV.









Trägt man die Thermospannung U gegen die Wassertemperatur T auf, so müsste man eine annähernd eine Gerade erhalten. Deren Steigung k entspricht dann genau der Differenz der beiden Seebeck-Koeffizienten der beiden Materialien SA – SB.
Metallpaarung Kupfer-Nickelchrom
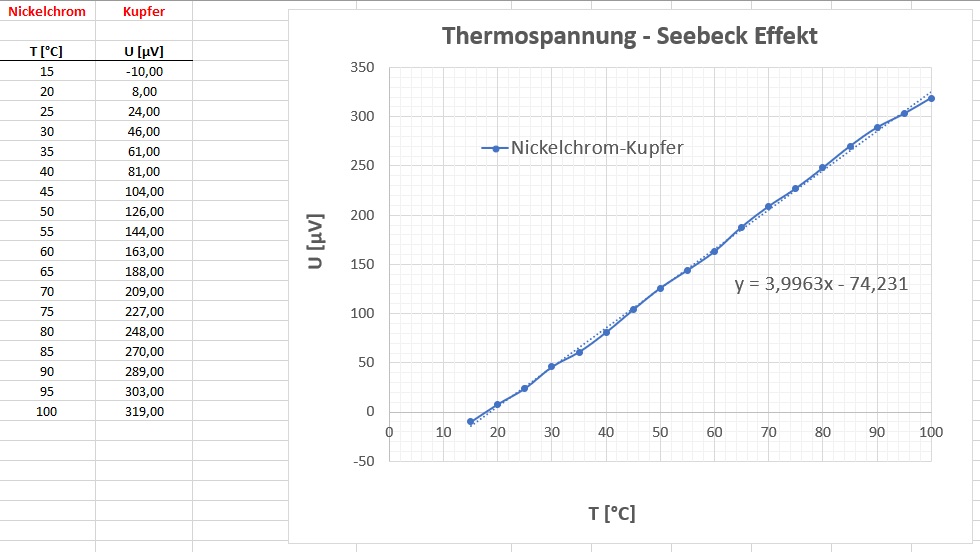

Für die Kombination Kupfer-Nickelchrom erhalte ich einen Wert SKupfer – SNickelchrom = 4 µV/K. Laut Tabelle (siehe oben) müsste ich allerdings einen Wert von 25 – 6.5 = 18.5 µV/K erhalten. Eine Recherche im Internet ergab aber, dass ich mit meinen 4 µV/K jedoch nicht so verkehrt liege:

Quelle: https://ap.physik.uni-konstanz.de/projektpraktikum/PP2012/Bericht-SeebeckEffekt.pdf
Hier nun die Ergebnisse/Graphen für andere Metallkombinationen:
Metallpaarung Kupfer-Eisen


Metallpaarung Kupfer-Konstantan


Eigenartigerweise stimmt für diese Paarung mein experimentelles Ergebnis überhaupt nicht mit dem theoretischen überein. Ich habe den Versuch mit einem anderen Kupferdraht nochmals wiederholt, aber das gleiche Ergebnis erhalten. Der Grund für diese Abweichung ist mir unklar. Ich werde aber der Sache nachgehen.
Da mir das Messergebnis keine Ruhe ließ, habe ich über ebay einen weiteren Konstantandraht aus Bulgarien bestellt. Dieser ist nun angekommen und ich konnte die Messung mit der Metallpaarung Kupfer-Konstantan wiederholen. Der damit erhaltene Wert liegt jetzt bei 51.5 µV/K und somit deutlich näher am Tabellenwert. 😉 Man muss aber auch anmerken, dass die Seebeck-Koeffizienten keine Konstanten sind, sondern ebenfalls von der Temperatur abhängen. Sie wachsen mit zunehmender Temperatur und die Tabellenwerte gelten für 273 K = 0°C. Meine Messungen lagen aber zwischen 20°C und 100°C.



Das Youtube-Video reiche ich wie immer nach…

