Im Jahr 1990 kaufte mir mein Vater fürs Studium einen damals brandaktuellen PC, konkret einen 386-er mit ganzen 33 MHz Taktrate und 42 MB Festplatte! Damit konnte ich in den darauffolgenden Jahren das eine oder andere Programm (zumeist in TurboPascal) aus dem Bereich Physik bzw. Astronomie schreiben.
Im Alter von 17 Jahren stieß ich zufällig in der amerikanischen Zeitschrift Astronomy (welche ich mir immer in einem Laden vornehmlich für Sexzeitschriften besorgte 😉 ) auf ein unscheinbares BASIC-Programm, welches trotz seiner wenigen Zeilen in der Lage zu sein schien, komplexe kosmische Bewegungen zu simulieren. Konkret ging es um die gravitative Wechselwirkung eines massereichen schwarzen Lochs mit dem Zentralkörper und den diesen umrundenden Sternen einer Galaxie.

Ich bin bei meiner Recherche nach dieser Zeitschrift fündig geworden. Es handelt sich bei der gesuchten Ausgabe um jene vom Dezember 1988. Auf den Seiten 90-96 wird unter dem Titel „Galactic collisions on your computer“ von Michael C. Schroeder und Neil F. Comins diese Simulation präsentiert.
Natürlich habe ich den Programmcode gleich abgeschrieben und ich war wirklich verblüfft zu sehen, wie nun das schwarze Loch völlig realistisch meine Galaxie am Computermonitor sukzessive verformte. Den mathematischen/physikalischen Hintergrund verstand ich damals noch nicht wirklich. Heute weiß ich, dass hinter der Simulation von damals das sog. Euler-Verfahren zur Lösung der Differentialgleichungen steckt. Das eulersche Polygonzugverfahren ist das einfachste Verfahren zur numerischen Lösung eines Anfangswertproblems. Es wurde von Leonhard Euler 1768 in seinem Buch Institutiones Calculi Integralis vorgestellt.
Was steckt dahinter? Nehmen wir unsere Astrosimulation. Die wirkenden Kräfte sind rein gravitativer Natur. Das Newtonsche Gravitationsgesetz beinhaltet zur Berechnung der Kraft zwischen 2 Himmelskörper neben der Gravitationskonstante G nur deren Massen M1 und M2 und deren Abstand d:
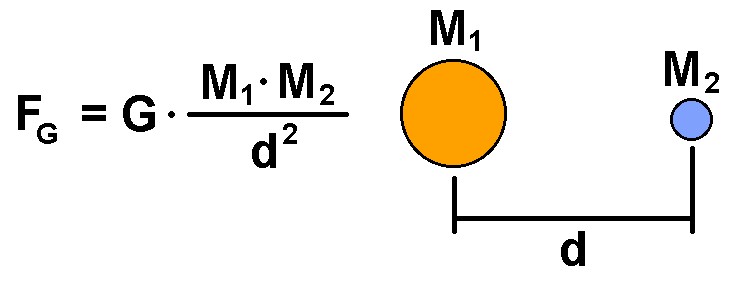
Kenne ich alle Positionen der Sterne, des Zentralkörpers und des schwarzen Lochs, so kann ich einmal die auf jedes dieser Objekte wirkende Gesamtkraft F berechnen. Was fange ich aber nun mit diesen Kraftvektoren an?
Das zweite Newtonsche Axiom beinhaltet die sog. Bewegungsgleichung
F = m · a.
Diese wohl wichtigste Formel der ganzen Mechanik verknüpft also die auf einen Körper wirkende Kraft F mit dessen Beschleunigung a. Kenne ich F, so kenne ich auch a. Wir kennen aber auch den Zusammenhang zwischen der Beschleunigung a und der Geschwindigkeitsänderung dv bzw. Δv innerhalb des Zeitintervalls dt bzw. Δt. Er lautet:
a = dv/dt (infinitesimal) bzw. bei größeren Zeitintervallen a = Δv/Δt.
Formt man diese Gleichung nach Δv = v(t + Δt) – v(t) um erhält man:
v(t + Δt) – v(t) = a · Δt bzw. v(t + Δt) = v(t) + a · Δt
Damit kennen wir also bereits die Geschwindigkeiten v(t + Δt), also zum etwas späteren Zeitpunkt t + Δt! Nun möchten wir nur noch die neuen Orte zum Zeitpunkt t + Δt kennen. Hierfür bedienen wir uns des Zusammenhangs zwischen v und der Ortsänderung ds bzw. Δs innerhalb des Zeitintervalls dt bzw. Δt. Er lautet:
v = ds/dt (infinitesimal) bzw. bei größeren Zeitintervallen v = Δs/Δt.
Mit dieser Beziehung sind wir [wie vorhin bei der Berechnung der Geschwindigkeit v(t + Δt)] in der Lage den aktualisierten Ort s(t + Δt) zum Zeitpunkt t + Δt zu berechnen. Es gilt:
Δs = s(t + Δt) – s(t) = v · Δt bzw. s(t + Δt) = s(t) + v · Δt
Welches v setzen wir aber nun hier ein? Wir könnten die Geschwindigkeit v(t) zu Beginn des betrachteten Zeitintervalls [t, t+Δt] einsetzen, was von der Herleitung her naheliegend erscheinen würde. Bezüglich der Geschwindigkeiten kennen wir aber jetzt nicht nur die Geschwindigkeit v(t) zu Beginn des betrachteten Zeitintervalls [t, t+Δt], sondern auch jene an dessen Ende in Form von v(t + Δt). Diesen Vorteil wollen wir natürlich nützen und setzen daher das arithmetische von v(t) und v(t + Δt) ein und erhalten
s(t + Δt) = s(t) + ½ · [v(t) + v(t + Δt)] · Δt
Wir kennen damit also nicht nur die „neuen“ Geschwindigkeiten zum Zeitpunkt t + Δt, sondern auch die aktualisierten Orte s(t + Δt) zum Zeitpunkt t + Δt. Und genau mit diesen neuen Werten werden abermals in Form einer Berechnungsschleife die aktuellen Kräfte F, Beschleunigungen a, Geschwindigkeiten v und Orte s berechnet. Dieses Spiel wiederholt sich immer wieder, was natürlich ein gefundenes Fressen für einen Blechtrottel ist. Hier kann er seine ganze Stärke ausspielen und vollführt tausende Berechnungen innerhalb einer einzelnen Sekunde.
Dieses Euler-Verfahren ist wie oben schon erwähnt das einfachste Verfahren zur Lösung dieses Anfangwertproblems. Es lässt sich aber im Gegensatz zu komplexeren Methoden (wie etwa das Runge-Kutta-Verfahren) auch für Schüler einigermaßen leicht nachvollziehen. Die Genauigkeit des Euler-Verfahrens hängt natürlich entscheidend von der gewählten Schrittweite Δt ab. Je feiner man diese wählt, umso genauer wird die Simulation bzw. umso später erst weicht dieses simple Verfahren deutlich von den realen Verhältnissen ab. Zum Abschluss also nochmals die grafische Zusammenfassung des hier zum Einsatz kommenden Euler-Verfahrens:
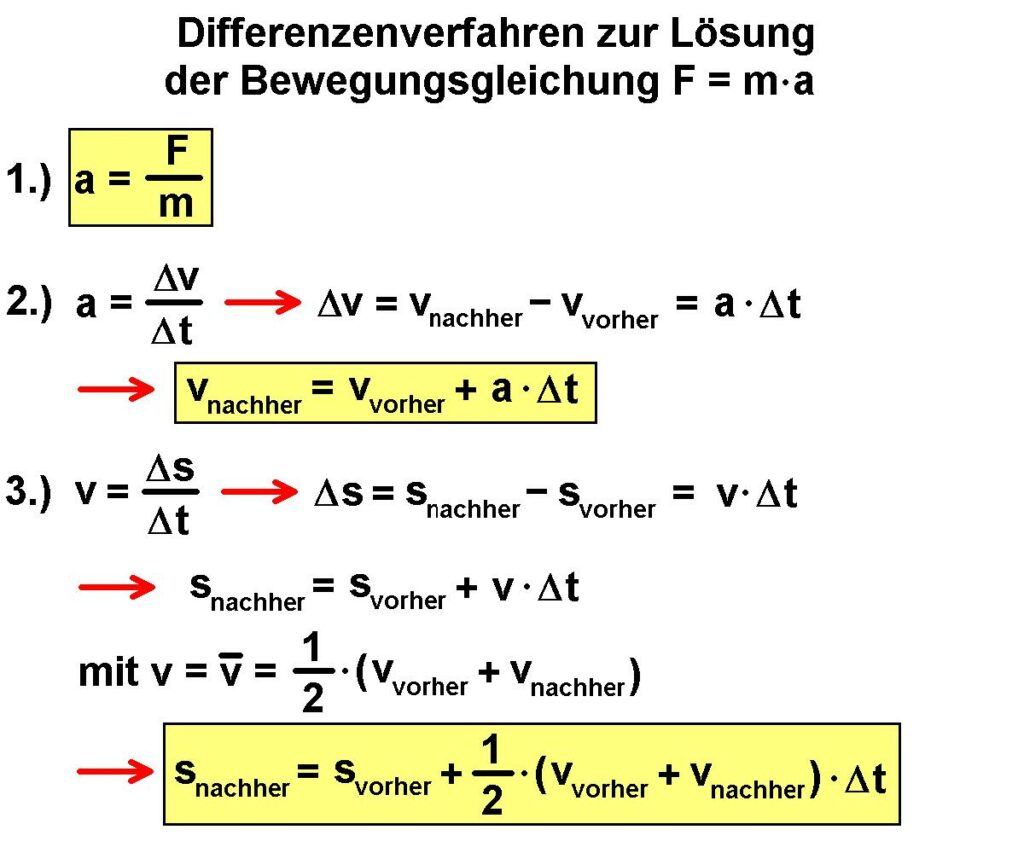
Mit diesem Verfahren habe ich etliche meiner astrophysikalischen Simulationen vom Sonnenanalemma bis hin zur Galaxienkollision berechnet. Einige davon werden nachfolgend kurz vorgestellt.
Sonnenanalemma

Bildquelle: https://de.wikipedia.org/wiki/Analemma
Fotografiert man die Sonne im Laufe einen ganzen Jahres immer zur selben Uhrzeit (z.B. 12 Uhr mittags), so ändert sich nicht nur die Höhe über dem Horizont (im Winter tiefer, im Sommer höher), sondern auch der sog. Azimut, also der Positionswinkel. Denn die Sonne befindet sich keinesfalls so wie man annehmen könnte um 12 Uhr mittags immer genau im Süden! Dies ist nur an 4 Tagen im Jahr genau der Fall. An allen anderen Tagen befindet sich die Sonne etwas in Richtung Osten (geht quasi nach) oder Westen (geht quasi vor).
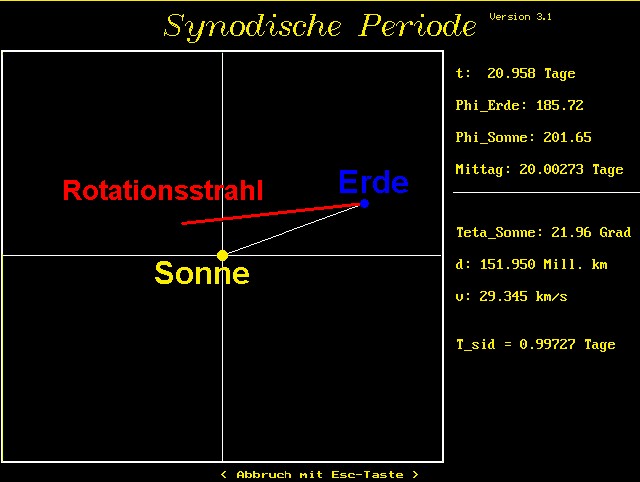
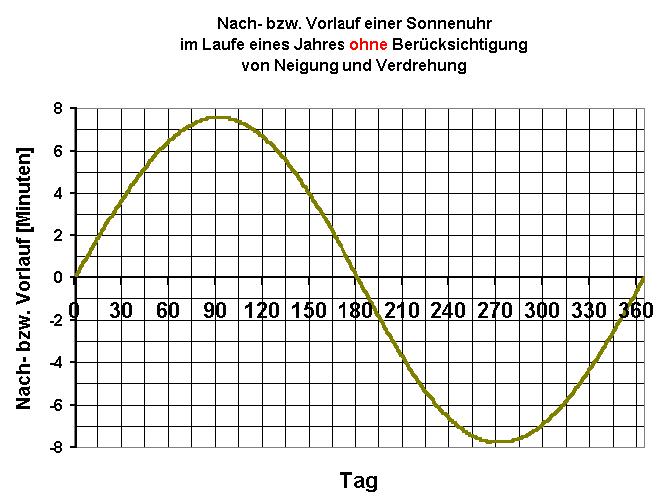
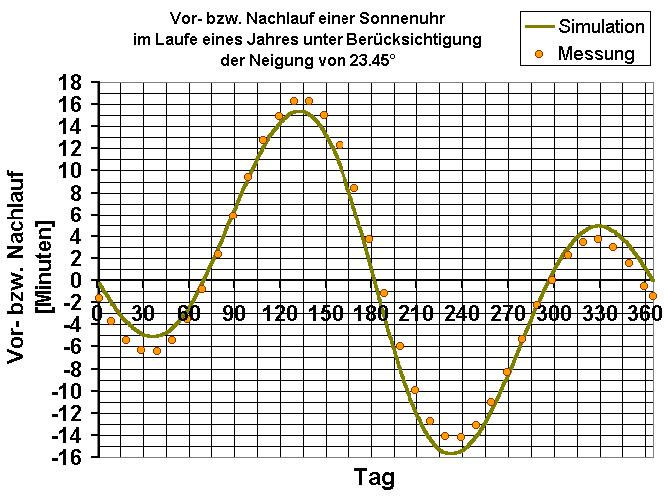
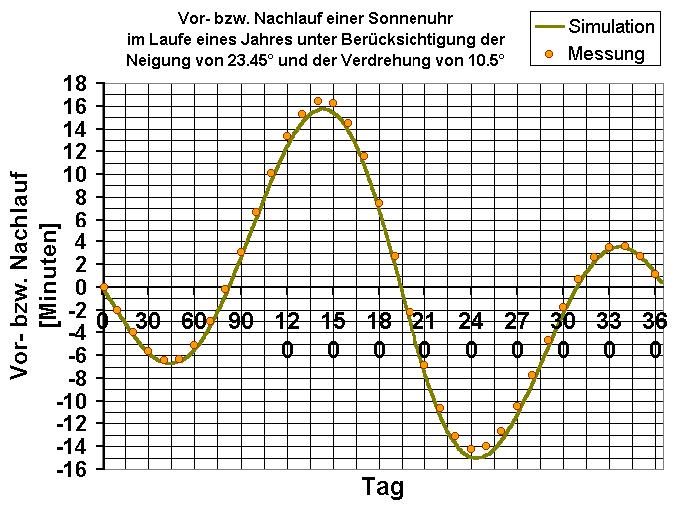
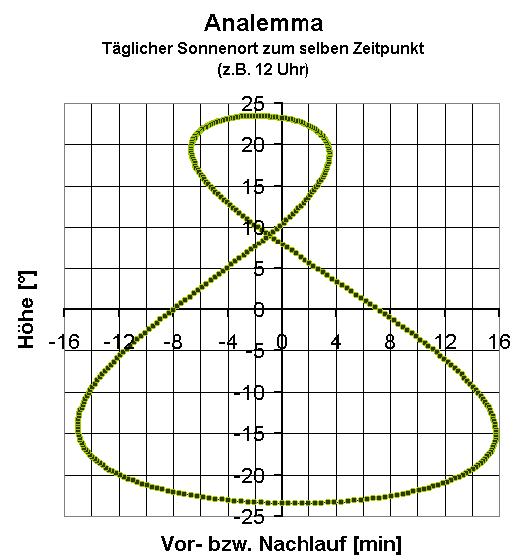
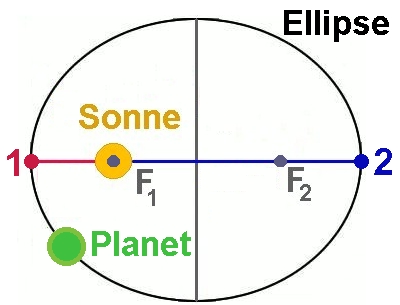
Basis der Berechnung des Analemmas war die Simulation der Erdbewegung um die Sonne im Laufe eines Jahres. Die Erde bewegt sich ja nach Johannes Kepler auf einer Ellipse um die Sonne, wobei sich diese in einem der beiden Brennpunkte befindet. In der unteren Abbildung ist die Exzentrizität der Erdbahn deutlich vergrößert dargestellt. In Wirklichkeit unterscheiden sich die Abstände Erde-Sonne in den Punkten 1 (Perihel) und 2 (Aphel) bedeutend weniger als skizziert.
Satellitensimulation
Die Simulation von Satellitenbahnen um die Erde ist deutlich einfacher als die Herleitung des Analemmas. Ich griff bei der Positionsberechnung des Satelliten abermals auf das Euler-Verfahren zurück. Mit dieser Simulation lässt sich etwa die erste kosmische Geschwindigkeit vI simulieren bzw. wie die Bahn aussieht, wenn der Satellit eine Geschwindigkeit größer bzw. kleiner als die für seinen Abstand notwendige Kreisbahngeschwindigkeit besitzt. Die Schüler erkennen dann sofort, dass sich dabei Ellipsenbahnen ergeben. Einen besonderen Spaß bereitet es natürlich den Schülern, den Satelliten abstürzen zu lassen…
Galaxienkollisionen
Diese Simulation wurde inspiriert durch den Eingangs bereits erwähnten Artikel in der Zeitschrift Astronomy Ende der 80-er Jahre. In der ersten Variante stört ein massereiches schwarzes Loch (dargestellt durch einen roten Kreis) eine Galaxie (deren massereicher Zentralkörper ist der grüne Kreis) und ihre Sterne (weiße Punkte).
In der zweiten Variante ersetze ich das schwarze Loch durch eine zweite vollständige Galaxie (roter Kreis und rote Sterne). Ziel war es, solche engen kosmischen Begegnungen wie sie etwa bei den beiden Mäusegalaxien NGC 4676 A und NGC 4676 B im Sternbild Haar der Berenike oder bei NGC4038 und NGC4039 im Sternbild Rabe stattgefunden haben zumindest ansatzweise zu simulieren.


Variante 1: Galaxie vs. Schwarzes Loch
Bei dieser Simulation tritt ein schwarzes Loch gegen eine Galaxie an, die über einen massereichen Zentralkörper verfügt. Dessen Masse und die Masse des schwarzen Lochs können mittels Potentiometer eingegeben werden. Zudem noch die Startposition (x/y/z) und Startgeschwindigkeit (vx/vy/vz) des schwarzen Lochs. Die Anzahl der Sterne in der Galaxie ist auch variabel, wobei aufgrund des limitierten Speichers des Arduino Due maximal 80 Sterne gewählt werden können.
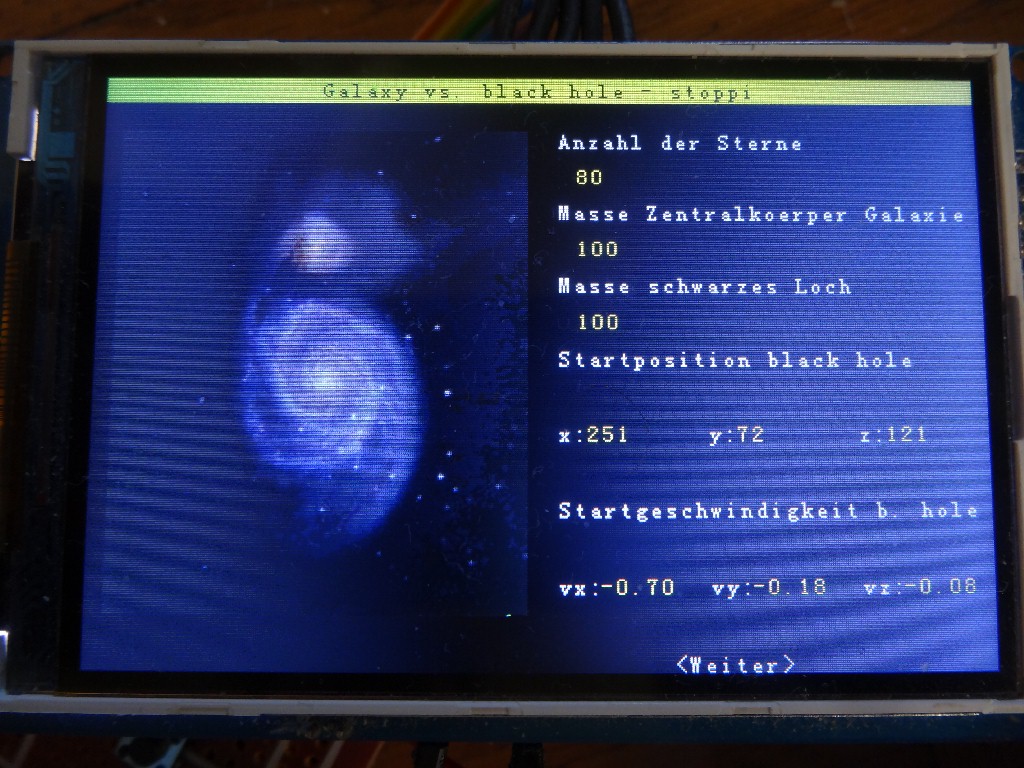
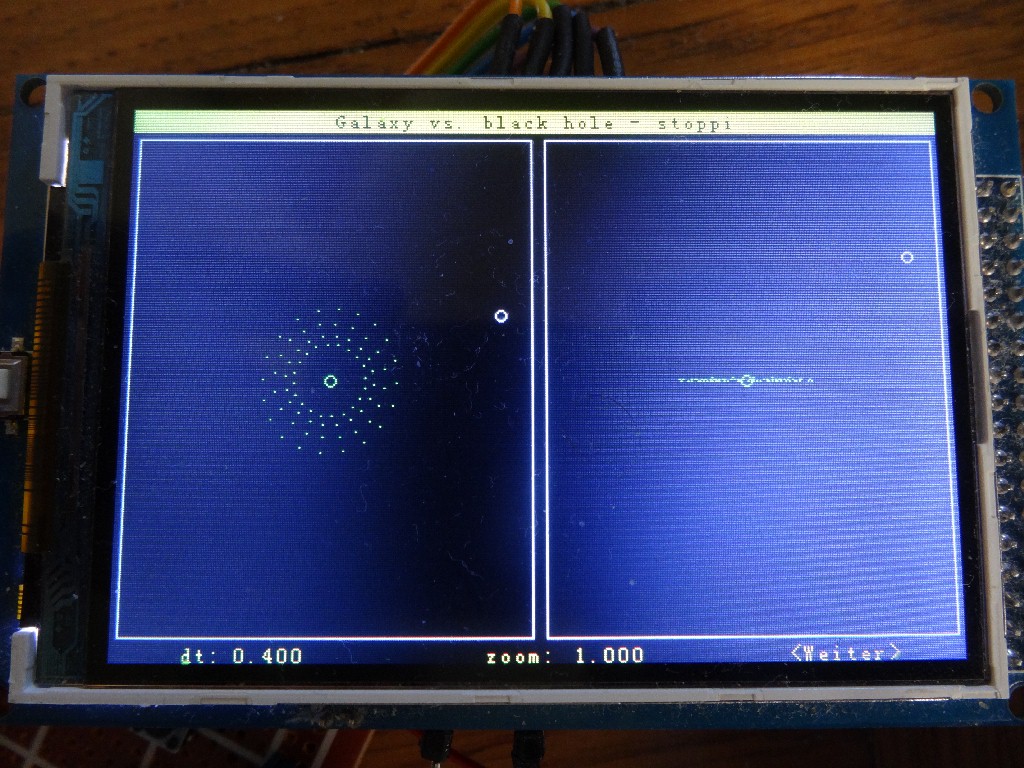
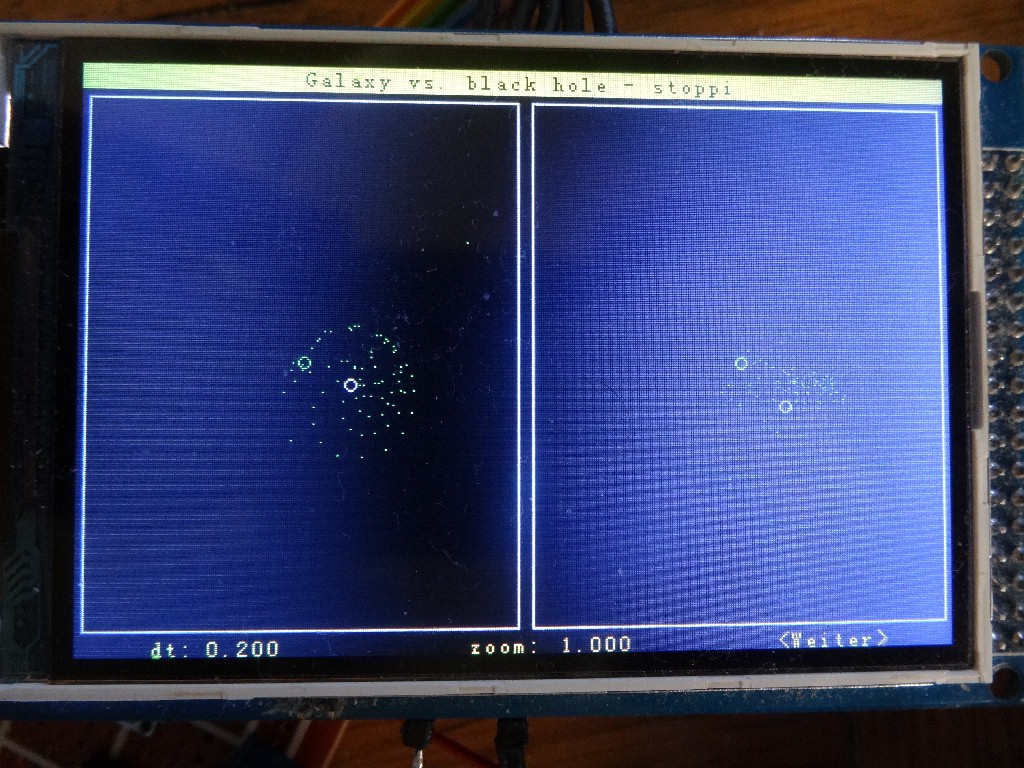
Nach der Werteeingabe gelangt man zur Simulation. In der linken Bildschirmhälfte wird die x-y Ansicht, rechts die x-z Ansicht ausgegeben. Mittels Taster sind die Zeitschrittweite dt und der Zoomfaktor einstellbar.
Arduino-Code:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299 300 301 302 303 304 305 306 307 308 309 310 311 312 313 314 315 316 317 318 319 320 321 322 323 324 325 326 327 328 329 330 331 332 333 334 335 336 337 338 339 340 341 342 343 344 345 346 347 348 349 350 351 352 353 354 355 356 357 358 359 360 361 362 363 364 365 366 367 368 369 370 371 372 373 374 375 376 377 378 379 380 381 382 383 384 385 386 387 388 389 390 391 392 393 394 395 396 397 398 399 400 401 402 403 404 405 406 407 408 409 410 411 412 413 414 415 416 417 418 419 420 421 422 423 424 425 426 427 428 429 430 431 432 433 434 435 436 437 438 439 440 441 442 443 444 445 446 447 448 449 450 451 452 453 454 455 456 457 458 459 460 461 462 463 464 465 466 467 468 469 470 471 472 473 474 475 476 477 478 479 480 481 482 483 484 485 486 487 488 489 490 491 492 493 494 495 496 497 498 499 500 501 502 503 504 505 506 507 508 509 510 511 512 513 514 515 516 517 518 519 520 521 522 523 524 525 526 527 528 529 530 531 532 533 534 535 536 537 538 539 540 541 542 543 544 545 546 547 548 549 550 551 552 553 554 555 556 557 558 559 560 561 562 563 564 565 566 567 568 569 570 571 572 573 574 575 576 577 578 579 580 581 582 583 584 585 586 587 588 589 590 591 592 593 594 595 596 597 598 599 600 601 602 603 604 605 606 607 608 609 610 611 612 613 614 615 616 617 618 619 620 621 622 623 624 625 626 627 628 629 630 631 632 633 634 635 636 637 638 639 640 641 642 643 644 645 646 647 648 649 650 651 652 653 654 655 656 657 658 659 660 661 662 663 664 665 666 667 668 669 670 671 672 673 674 675 676 677 678 679 680 |
#include <UTFT.h> // Declare which fonts we will be using extern uint8_t SmallFont[]; UTFT myGLCD(ILI9486,38,39,40,41); extern unsigned short M51[0xE350]; float vx_vorher[82], vy_vorher[82], vz_vorher[82]; // Geschwindigkeiten vor dem Zeitschritt in x-, y- und z-Richtung float vx_nachher[82], vy_nachher[82], vz_nachher[82]; // Geschwindigkeiten nach dem Zeitschritt in x-, y- und z-Richtung float sx_vorher[82], sy_vorher[82], sz_vorher[82]; // Orte vor dem Zeitschritt in x-, y- und z-Richtung float sx_nachher[82], sy_nachher[82], sz_nachher[82]; // Orte nach dem Zeitschritt in x-, y- und z-Richtung float Kraft_x[82] [82]; // Kraftmatrix für alle Wechselwirkungen zwischen allen Massen float Kraft_y[82] [82]; // Kraftmatrix für alle Wechselwirkungen zwischen allen Massen float Kraft_z[82] [82]; // Kraftmatrix für alle Wechselwirkungen zwischen allen Massen float m[82]; // Masse der Objekte // Hinweis: Zentralkörper Galaxie = Index 0, Sterne Galaxie = Index 1 bis n // Schwarzes Loch = Index n+1 // ======================================================================== float Force_x, Force_y, Force_z; // die auf das Objekt wirkende Kraft in x- und y-Richtung float delta_t, t, time_step; // Zeitschrittweite und aktuelle Zeit bzw. Zeitdauer für eine komplette Berechnung float Vergroesserung; // Vergrößerungsfaktor bei der grafischen Darstellung int n; // Anzahl der Objekte ohne Zentralkörper und ohne schwarzes Loch. n muss durch 4 teilbar sein! int zaehler, i, j; // Zählvariable const float Pi = 3.141592653589; const float rad = Pi / 180.0; const int Pin_continue = 6; const int Pin_fast = 5; const int Pin_slow = 4; const int Pin_zoom_in = 3; const int Pin_zoom_out = 2; int Pin_value = A0; int sensorValue; // ================= // == SETUP == // ================= void setup() { Serial.begin(9600); // Init serial interface pinMode(Pin_continue, INPUT); pinMode(Pin_fast, INPUT); pinMode(Pin_slow, INPUT); pinMode(Pin_zoom_in, INPUT); pinMode(Pin_zoom_out, INPUT); // Setup the LCD myGLCD.InitLCD(); myGLCD.setFont(SmallFont); } // ================ // == LOOP == // ================ void loop() { myGLCD.clrScr(); myGLCD.setColor(255, 255, 0); myGLCD.fillRect(0, 0, 479, 13); myGLCD.setColor(0, 0, 0); myGLCD.setBackColor(255, 255, 0); myGLCD.print("Galaxy vs. black hole - stoppi", CENTER, 1); myGLCD.drawBitmap (10, 30, 223, 261, M51); myGLCD.setColor(255, 255, 255); myGLCD.setBackColor(0, 0, 0); myGLCD.print("Anzahl der Sterne", 250, 30); myGLCD.print("Masse Zentralkoerper Galaxie", 250, 70); myGLCD.print("Masse schwarzes Loch", 250, 110); myGLCD.print("Startposition black hole", 250, 150); myGLCD.print("x:", 250, 190); myGLCD.print("y:", 330, 190); myGLCD.print("z:", 410, 190); myGLCD.print("Startgeschwindigkeit b. hole", 250, 230); myGLCD.print("vx:", 250, 270); myGLCD.print("vy:", 330, 270); myGLCD.print("vz:", 410, 270); myGLCD.print("<Weiter>", 310, 310); delay(1000); // ====================== // === WERTEEINGABE === // ====================== while(digitalRead(Pin_continue)) { sensorValue = analogRead(Pin_value); n = map(sensorValue,0,1023,1,20); n = 4 * n; myGLCD.setColor(0,0,0); myGLCD.fillRect(260,50,310,60); myGLCD.setColor(255, 255, 0); myGLCD.printNumI(n,260,50); //myGLCD.printNumF(n, 3, 260,50); delay(10); } delay(300); while(digitalRead(Pin_continue)) { sensorValue = analogRead(Pin_value); m[0] = map(sensorValue,0,1023,1,100); myGLCD.setColor(0,0,0); myGLCD.fillRect(260,90,310,100); myGLCD.setColor(255, 255, 0); myGLCD.printNumI(m[0],260,90); //myGLCD.printNumF(m[0], 3, 260,50); delay(10); } delay(300); while(digitalRead(Pin_continue)) { sensorValue = analogRead(Pin_value); m[n+1] = map(sensorValue,0,1023,1,100); myGLCD.setColor(0,0,0); myGLCD.fillRect(260,130,310,140); myGLCD.setColor(255, 255, 0); myGLCD.printNumI(m[n+1],260,130); //myGLCD.printNumF(m[n+1], 3, 260,130); delay(10); } delay(300); while(digitalRead(Pin_continue)) { sensorValue = analogRead(Pin_value); sx_vorher[n+1] = map(sensorValue,0,1023,50,500); myGLCD.setColor(0,0,0); myGLCD.fillRect(265,190,315,200); myGLCD.setColor(255, 255, 0); myGLCD.printNumI(sx_vorher[n+1],265,190); //myGLCD.printNumF(sx_vorher[n+1], 3, 265,190); delay(10); } delay(300); while(digitalRead(Pin_continue)) { sensorValue = analogRead(Pin_value); sy_vorher[n+1] = map(sensorValue,0,1023,-200,200); myGLCD.setColor(0,0,0); myGLCD.fillRect(345,190,395,200); myGLCD.setColor(255, 255, 0); myGLCD.printNumI(sy_vorher[n+1],345,190); //myGLCD.printNumF(sy_vorher[n+1], 0, 345,190); delay(10); } delay(300); while(digitalRead(Pin_continue)) { sensorValue = analogRead(Pin_value); sz_vorher[n+1] = map(sensorValue,0,1023,-200,200); myGLCD.setColor(0,0,0); myGLCD.fillRect(425,190,475,200); myGLCD.setColor(255, 255, 0); myGLCD.printNumI(sz_vorher[n+1],425,190); //myGLCD.printNumF(sz_vorher[n+1], 0, 425,190); delay(10); } delay(300); while(digitalRead(Pin_continue)) { sensorValue = analogRead(Pin_value); vx_vorher[n+1] = map(sensorValue,0,1023,-100,0); vx_vorher[n+1] = vx_vorher[n+1] / 50.0; myGLCD.setColor(0,0,0); myGLCD.fillRect(272,270,322,280); myGLCD.setColor(255, 255, 0); //myGLCD.printNumI(vx_vorher[n+1],272,270); myGLCD.printNumF(vx_vorher[n+1], 2, 272,270); delay(10); } delay(300); while(digitalRead(Pin_continue)) { sensorValue = analogRead(Pin_value); vy_vorher[n+1] = map(sensorValue,0,1023,-100,100); vy_vorher[n+1] = vy_vorher[n+1] / 50.0; myGLCD.setColor(0,0,0); myGLCD.fillRect(352,270,402,280); myGLCD.setColor(255, 255, 0); //myGLCD.printNumI(vy_vorher[n+1],352,270); myGLCD.printNumF(vy_vorher[n+1], 2, 352,270); delay(10); } delay(300); while(digitalRead(Pin_continue)) { sensorValue = analogRead(Pin_value); vz_vorher[n+1] = map(sensorValue,0,1023,-100,100); vz_vorher[n+1] = vz_vorher[n+1] / 50.0; myGLCD.setColor(0,0,0); myGLCD.fillRect(432,270,480,280); myGLCD.setColor(255, 255, 0); //myGLCD.printNumI(vz_vorher[n+1],432,270); myGLCD.printNumF(vz_vorher[n+1], 2, 432,270); delay(10); } delay(300); // ====================== // === SIMULATION === // ====================== myGLCD.clrScr(); myGLCD.setColor(255, 255, 0); myGLCD.fillRect(0, 0, 479, 13); myGLCD.setColor(0, 0, 0); myGLCD.setBackColor(255, 255, 0); myGLCD.print("Galaxy vs. black hole - stoppi", CENTER, 1); sx_vorher[0] = 0.0; // Start-Standort des Zentralkörpers der Galaxie sy_vorher[0] = 0.0; sz_vorher[0] = 0.0; vx_vorher[0] = 0.0; vy_vorher[0] = 0.0; vz_vorher[0] = 0.0; t = 0.0; delta_t = 0.2; Vergroesserung = 1; // Stern-Initialisierung // ===================== for (i = 1; i <= n; i++) { m[i] = 0.01; // Masse eines Sterns der Galaxie } zaehler = 0; for (j = 1; j <= 4; j++) // Festlegung der Stern-Startorte und Geschwindigkeiten der Galaxie 1 { for (i = 0; i < n/4; i++) { zaehler = zaehler + 1; sx_vorher[zaehler] = 10.0 * j * cos(rad * 360.0 * i * 4 / n); sy_vorher[zaehler] = 10.0 * j * sin(rad * 360.0 * i * 4 / n); sz_vorher[zaehler] = 0.0; vx_vorher[zaehler] = -sin(rad * 360 * i * 4 / n) * sqrt(m[0] / sqrt(sx_vorher[zaehler] * sx_vorher[zaehler] + sy_vorher[zaehler] * sy_vorher[zaehler])); vy_vorher[zaehler] = cos(rad * 360 * i * 4 / n) * sqrt(m[0] / sqrt(sx_vorher[zaehler] * sx_vorher[zaehler] + sy_vorher[zaehler] * sy_vorher[zaehler])); vz_vorher[zaehler] = 0.0; } } for(i = 0; i <= n+1; i++) // Kraft auf sich selbst ist 0 { Kraft_x [i] [i] = 0; Kraft_y [i] [i] = 0; Kraft_z [i] [i] = 0; } myGLCD.setBackColor(0, 0, 0); myGLCD.setColor(255, 255, 0); myGLCD.print("dt: ", 40, 310); myGLCD.setColor(0,0,0); myGLCD.fillRect(70,310,120,320); myGLCD.setColor(255, 255, 0); myGLCD.printNumF(delta_t, 3, 70, 310); myGLCD.print("zoom: ", 210, 310); myGLCD.setColor(0,0,0); myGLCD.fillRect(260,310,310,320); myGLCD.setColor(255, 255, 0); myGLCD.printNumF(Vergroesserung, 3, 260, 310); myGLCD.print("<Weiter>", 380, 310); // =============================== // Start der grafischen Simulation // =============================== while(digitalRead(Pin_continue)) { // Rahmen zeichnen // =============== myGLCD.setColor(255, 255, 255); myGLCD.drawLine(4,18,236,18); myGLCD.drawLine(4,18,4,306); myGLCD.drawLine(236,18,236,306); myGLCD.drawLine(4,306,236,306); myGLCD.drawLine(244,18,476,18); myGLCD.drawLine(244,18,244,306); myGLCD.drawLine(476,18,476,306); myGLCD.drawLine(244,306,476,306); myGLCD.setColor(255, 255, 0); // =================== // === Key pressed === // =================== if(digitalRead(Pin_fast)) { delta_t = delta_t * 2.0; myGLCD.setColor(0,0,0); myGLCD.fillRect(70,310,120,320); myGLCD.setColor(255, 255, 0); myGLCD.printNumF(delta_t, 3, 70,310); delay(300); } if(digitalRead(Pin_slow)) { delta_t = delta_t / 2.0; myGLCD.setColor(0,0,0); myGLCD.fillRect(70,310,120,320); myGLCD.setColor(255, 255, 0); myGLCD.printNumF(delta_t, 3, 70,310); delay(300); } if(digitalRead(Pin_zoom_in)) { myGLCD.setColor(0, 0, 0); if(abs(Vergroesserung * sx_vorher[0]) <= 115 && abs(Vergroesserung * sy_vorher[0]) <= 143) { myGLCD.drawCircle((int) 120 + Vergroesserung * sx_vorher[0], (int) 162 - Vergroesserung * sy_vorher[0], 3); } if(abs(Vergroesserung * sx_vorher[0]) <= 115 && abs(Vergroesserung * sz_vorher[0]) <= 143) { myGLCD.drawCircle((int) 360 + Vergroesserung * sx_vorher[0], (int) 162 - Vergroesserung * sz_vorher[0], 3); } if(abs(Vergroesserung * sx_vorher[n+1]) <= 115 && abs(Vergroesserung * sy_vorher[n+1]) <= 143) { myGLCD.drawCircle((int) 120 + Vergroesserung * sx_vorher[n+1], (int) 162 - Vergroesserung * sy_vorher[n+1], 3); } if(abs(Vergroesserung * sx_vorher[n+1]) <= 115 && abs(Vergroesserung * sz_vorher[n+1]) <= 143) { myGLCD.drawCircle((int) 360 + Vergroesserung * sx_vorher[n+1], (int) 162 - Vergroesserung * sz_vorher[n+1], 3); } for(i = 1; i <= n; i++) { if(abs(Vergroesserung * sx_vorher[i]) <= 115 && abs(Vergroesserung * sy_vorher[i]) <= 143) { myGLCD.drawPixel((int) 120 + Vergroesserung * sx_vorher[i], (int) 162 - Vergroesserung * sy_vorher[i]); } } for(i = 1; i <= n; i++) { if(abs(Vergroesserung * sx_vorher[i]) <= 115 && abs(Vergroesserung * sz_vorher[i]) <= 143) { myGLCD.drawPixel((int) 360 + Vergroesserung * sx_vorher[i], (int) 162 - Vergroesserung * sz_vorher[i]); } } Vergroesserung = Vergroesserung * 2.0; myGLCD.setColor(0,0,0); myGLCD.fillRect(260,310,310,320); myGLCD.setColor(255, 255, 0); myGLCD.printNumF(Vergroesserung, 3, 260,310); delay(300); } if(digitalRead(Pin_zoom_out)) { myGLCD.setColor(0, 0, 0); if(abs(Vergroesserung * sx_vorher[0]) <= 115 && abs(Vergroesserung * sy_vorher[0]) <= 143) { myGLCD.drawCircle((int) 120 + Vergroesserung * sx_vorher[0], (int) 162 - Vergroesserung * sy_vorher[0], 3); } if(abs(Vergroesserung * sx_vorher[0]) <= 115 && abs(Vergroesserung * sz_vorher[0]) <= 143) { myGLCD.drawCircle((int) 360 + Vergroesserung * sx_vorher[0], (int) 162 - Vergroesserung * sz_vorher[0], 3); } if(abs(Vergroesserung * sx_vorher[n+1]) <= 115 && abs(Vergroesserung * sy_vorher[n+1]) <= 143) { myGLCD.drawCircle((int) 120 + Vergroesserung * sx_vorher[n+1], (int) 162 - Vergroesserung * sy_vorher[n+1], 3); } if(abs(Vergroesserung * sx_vorher[n+1]) <= 115 && abs(Vergroesserung * sz_vorher[n+1]) <= 143) { myGLCD.drawCircle((int) 360 + Vergroesserung * sx_vorher[n+1], (int) 162 - Vergroesserung * sz_vorher[n+1], 3); } for(i = 1; i <= n; i++) { if(abs(Vergroesserung * sx_vorher[i]) <= 115 && abs(Vergroesserung * sy_vorher[i]) <= 143) { myGLCD.drawPixel((int) 120 + Vergroesserung * sx_vorher[i], (int) 162 - Vergroesserung * sy_vorher[i]); } } for(i = 1; i <= n; i++) { if(abs(Vergroesserung * sx_vorher[i]) <= 115 && abs(Vergroesserung * sz_vorher[i]) <= 143) { myGLCD.drawPixel((int) 360 + Vergroesserung * sx_vorher[i], (int) 162 - Vergroesserung * sz_vorher[i]); } } Vergroesserung = Vergroesserung / 2.0; myGLCD.setColor(0,0,0); myGLCD.fillRect(260,310,310,320); myGLCD.setColor(255, 255, 0); myGLCD.printNumF(Vergroesserung, 3, 260,310); delay(300); } // ======================================================================= // Berechnung der neuen Orte und Geschwindigkeiten mittels Euler-Verfahren // ======================================================================= //time_step = millis(); Euler(); // Alte Bildpunkte löschen // ======================= myGLCD.setColor(0, 0, 0); if(abs(Vergroesserung * sx_vorher[0]) <= 115 && abs(Vergroesserung * sy_vorher[0]) <= 143) { myGLCD.drawCircle((int) 120 + Vergroesserung * sx_vorher[0], (int) 162 - Vergroesserung * sy_vorher[0], 3); } if(abs(Vergroesserung * sx_vorher[0]) <= 115 && abs(Vergroesserung * sz_vorher[0]) <= 143) { myGLCD.drawCircle((int) 360 + Vergroesserung * sx_vorher[0], (int) 162 - Vergroesserung * sz_vorher[0], 3); } if(abs(Vergroesserung * sx_vorher[n+1]) <= 115 && abs(Vergroesserung * sy_vorher[n+1]) <= 143) { myGLCD.drawCircle((int) 120 + Vergroesserung * sx_vorher[n+1], (int) 162 - Vergroesserung * sy_vorher[n+1], 3); } if(abs(Vergroesserung * sx_vorher[n+1]) <= 115 && abs(Vergroesserung * sz_vorher[n+1]) <= 143) { myGLCD.drawCircle((int) 360 + Vergroesserung * sx_vorher[n+1], (int) 162 - Vergroesserung * sz_vorher[n+1], 3); } for(i = 1; i <= n; i++) { if(abs(Vergroesserung * sx_vorher[i]) <= 115 && abs(Vergroesserung * sy_vorher[i]) <= 143) { myGLCD.drawPixel((int) 120 + Vergroesserung * sx_vorher[i], (int) 162 - Vergroesserung * sy_vorher[i]); } } for(i = 1; i <= n; i++) { if(abs(Vergroesserung * sx_vorher[i]) <= 115 && abs(Vergroesserung * sz_vorher[i]) <= 143) { myGLCD.drawPixel((int) 360 + Vergroesserung * sx_vorher[i], (int) 162 - Vergroesserung * sz_vorher[i]); } } // Werteübergabe und Ortsverschiebung // ================================== for (i = 0; i <= n+1; i++) { sx_vorher[i] = sx_nachher[i] - sx_nachher[0]; // Werteübergabe der Orte und Verschiebung, da Zentralkörper immer im Punkt (0,0) sy_vorher[i] = sy_nachher[i] - sy_nachher[0]; // Werteübergabe der Orte und Verschiebung, da Zentralkörper immer im Punkt (0,0) sz_vorher[i] = sz_nachher[i] - sz_nachher[0]; // Werteübergabe der Orte und Verschiebung, da Zentralkörper immer im Punkt (0,0) vx_vorher[i] = vx_nachher[i]; // Werteübergabe der Geschwindigkeiten in x-Richtung vy_vorher[i] = vy_nachher[i]; // Werteübergabe der Geschwindigkeiten in y-Richtung vz_vorher[i] = vz_nachher[i]; // Werteübergabe der Geschwindigkeiten in z-Richtung } // neue Orte zeichnen // ================== myGLCD.setColor(0, 255, 0); if(abs(Vergroesserung * sx_vorher[0]) <= 115 && abs(Vergroesserung * sy_vorher[0]) <= 143) { myGLCD.drawCircle((int) 120 + Vergroesserung * sx_vorher[0], (int) 162 - Vergroesserung * sy_vorher[0], 3); } if(abs(Vergroesserung * sx_vorher[0]) <= 115 && abs(Vergroesserung * sz_vorher[0]) <= 143) { myGLCD.drawCircle((int) 360 + Vergroesserung * sx_vorher[0], (int) 162 - Vergroesserung * sz_vorher[0], 3); } for(i = 1; i <= n; i++) { if(abs(Vergroesserung * sx_vorher[i]) <= 115 && abs(Vergroesserung * sy_vorher[i]) <= 143) { myGLCD.drawPixel((int) 120 + Vergroesserung * sx_vorher[i], (int) 162 - Vergroesserung * sy_vorher[i]); } } for(i = 1; i <= n; i++) { if(abs(Vergroesserung * sx_vorher[i]) <= 115 && abs(Vergroesserung * sz_vorher[i]) <= 143) { myGLCD.drawPixel((int) 360 + Vergroesserung * sx_vorher[i], (int) 162 - Vergroesserung * sz_vorher[i]); } } myGLCD.setColor(255, 255, 255); if(abs(Vergroesserung * sx_vorher[n+1]) <= 115 && abs(Vergroesserung * sy_vorher[n+1]) <= 143) { myGLCD.drawCircle((int) 120 + Vergroesserung * sx_vorher[n+1], (int) 162 - Vergroesserung * sy_vorher[n+1], 3); } if(abs(Vergroesserung * sx_vorher[n+1]) <= 115 && abs(Vergroesserung * sz_vorher[n+1]) <= 143) { myGLCD.drawCircle((int) 360 + Vergroesserung * sx_vorher[n+1], (int) 162 - Vergroesserung * sz_vorher[n+1], 3); } t = t + delta_t; //Serial.println(millis() - time_step); //delay(500); //Serial.println(sx_nachher[2]); } } // ============================== // === UNTERPROGRAMM FORCE === // ============================== void Force() { float distance; // Distanz zwischen zwei Objekten i_Force und j_Force float einheit_x, einheit_y, einheit_z; // Einheitsvektor in x-, y- bzw. z-Richtung zwischen zwei Objekten k_Force und l_Force int k_Force, l_Force; // Zählvariablen for(k_Force = 0; k_Force <= n; k_Force++) { for(l_Force = k_Force + 1; l_Force <= n+1; l_Force++) { distance = sqrt((sx_vorher[l_Force] - sx_vorher[k_Force]) * (sx_vorher[l_Force] - sx_vorher[k_Force]) + (sy_vorher[l_Force] - sy_vorher[k_Force]) * (sy_vorher[l_Force] - sy_vorher[k_Force]) + (sz_vorher[l_Force] - sz_vorher[k_Force]) * (sz_vorher[l_Force] - sz_vorher[k_Force])); // Berechnung des Einheitsvektors in Richtung der Verbindungsgeraden der beiden Massen einheit_x = (1.0 / distance) * (sx_vorher[l_Force] - sx_vorher[k_Force]); einheit_y = (1.0 / distance) * (sy_vorher[l_Force] - sy_vorher[k_Force]); einheit_z = (1.0 / distance) * (sz_vorher[l_Force] - sz_vorher[k_Force]); Kraft_x [k_Force] [l_Force] = (m[k_Force] * m[l_Force] / (distance * distance)) * einheit_x; Kraft_y [k_Force] [l_Force] = (m[k_Force] * m[l_Force] / (distance * distance)) * einheit_y; Kraft_z [k_Force] [l_Force] = (m[k_Force] * m[l_Force] / (distance * distance)) * einheit_z; /* Serial.print("F["); Serial.print(k_Force); Serial.print(","); Serial.print(l_Force); Serial.print("] = "); Serial.print(Kraft_x [k_Force] [l_Force]); Serial.print(" "); Serial.println(Kraft_y [k_Force] [l_Force]); delay(500); */ Kraft_x [l_Force] [k_Force] = -Kraft_x [k_Force] [l_Force]; Kraft_y [l_Force] [k_Force] = -Kraft_y [k_Force] [l_Force]; Kraft_z [l_Force] [k_Force] = -Kraft_z [k_Force] [l_Force]; } } } // ======================= // == EULER-Verfahren == // ======================= void Euler() { int i_Euler, j_Euler; // Zählvariablen Force(); for (i_Euler = 0; i_Euler <= n+1; i_Euler++) { Force_x = 0; Force_y = 0; Force_z = 0; for (j_Euler = 0; j_Euler <= n+1; j_Euler++) { Force_x = Force_x + Kraft_x [i_Euler] [j_Euler]; Force_y = Force_y + Kraft_y [i_Euler] [j_Euler]; Force_z = Force_z + Kraft_z [i_Euler] [j_Euler]; } vx_nachher[i_Euler] = vx_vorher[i_Euler] + delta_t * (1.0 / m[i_Euler]) * Force_x; vy_nachher[i_Euler] = vy_vorher[i_Euler] + delta_t * (1.0 / m[i_Euler]) * Force_y; vz_nachher[i_Euler] = vz_vorher[i_Euler] + delta_t * (1.0 / m[i_Euler]) * Force_z; sx_nachher[i_Euler] = sx_vorher[i_Euler] + delta_t * 0.5 * (vx_vorher[i_Euler] + vx_nachher[i_Euler]); sy_nachher[i_Euler] = sy_vorher[i_Euler] + delta_t * 0.5 * (vy_vorher[i_Euler] + vy_nachher[i_Euler]); sz_nachher[i_Euler] = sz_vorher[i_Euler] + delta_t * 0.5 * (vz_vorher[i_Euler] + vz_nachher[i_Euler]); } } |
Bilddatei der Galaxie M51: M51
Variante 2: Galaxie vs. Galaxie
Bei der zweiten Variante wird das schwarze Loch gegen eine weitere Galaxie ausgetauscht. Die Masse der beiden Zentralkörper ist ebenso einstellbar wie die Startposition (x/y) und Startgeschwindigkeit (vx/vy) der zweiten Galaxie. Die Anzahl der Sterne pro Galaxie ist hier aufgrund des Arbeitsspeichers auf 40 Sterne beschränkt.
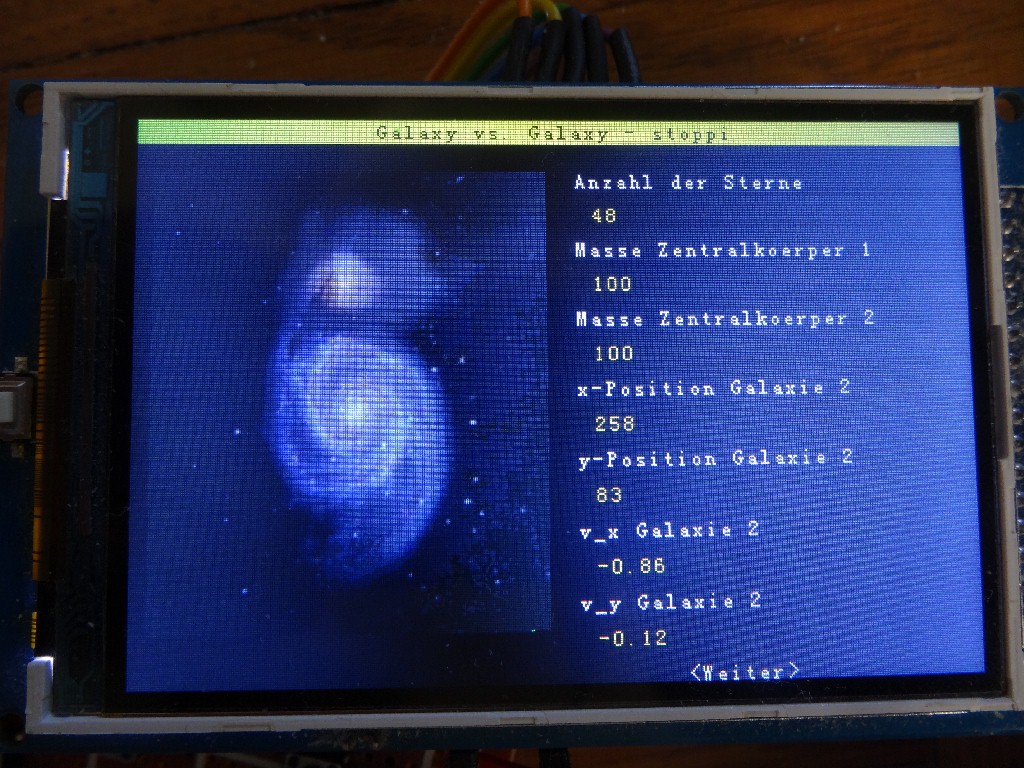
Da sich diese Simulation nur in der x-y-Ebene abspielt, ist der Bildschirm nicht zweigeteilt. Zu sehen ist die Draufsicht der beiden sich nähernden Galaxien.
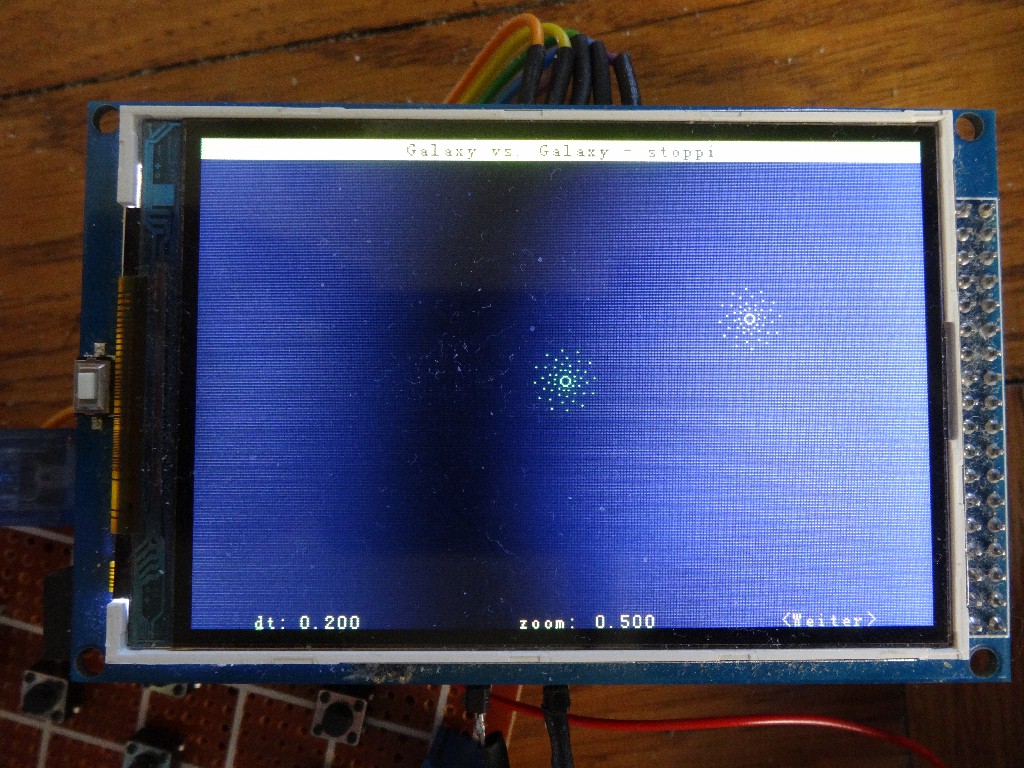

Während der Simulation sind wieder wie bei der Variante 1 die Zeitschritte dt und der Zoomfaktor veränderbar.
Arduino-Code:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299 300 301 302 303 304 305 306 307 308 309 310 311 312 313 314 315 316 317 318 319 320 321 322 323 324 325 326 327 328 329 330 331 332 333 334 335 336 337 338 339 340 341 342 343 344 345 346 347 348 349 350 351 352 353 354 355 356 357 358 359 360 361 362 363 364 365 366 367 368 369 370 371 372 373 374 375 376 377 378 379 380 381 382 383 384 385 386 387 388 389 390 391 392 393 394 395 396 397 398 399 400 401 402 403 404 405 406 407 408 409 410 411 412 413 414 415 416 417 418 419 420 421 422 423 424 425 426 427 428 429 430 431 432 433 434 435 436 437 438 439 440 441 442 443 444 445 446 447 448 449 450 451 452 453 454 455 456 457 458 459 460 461 462 463 464 465 466 467 468 469 470 471 472 473 474 475 476 477 478 479 480 481 482 483 484 485 486 487 488 489 490 491 492 493 494 495 496 497 498 499 500 501 502 503 504 505 506 507 508 509 510 511 512 513 514 515 516 517 518 519 520 521 522 523 524 525 526 527 528 529 530 531 532 533 534 535 536 537 538 539 540 541 542 543 544 545 546 547 548 549 550 551 552 553 554 555 556 557 558 559 560 561 562 563 564 565 566 567 568 569 570 571 572 573 574 575 576 577 578 579 580 581 582 583 584 585 586 587 588 589 |
#include <UTFT.h> // Declare which fonts we will be using extern uint8_t SmallFont[]; UTFT myGLCD(ILI9486,38,39,40,41); extern unsigned short M51[0xE350]; float vx_vorher[102], vy_vorher[102]; // Geschwindigkeiten vor dem Zeitschritt in x- und y-Richtung float vx_nachher[102], vy_nachher[102]; // Geschwindigkeiten nach dem Zeitschritt in x- und y-Richtung float sx_vorher[102], sy_vorher[102]; // Orte vor dem Zeitschritt in x- und y-Richtung float sx_nachher[102], sy_nachher[102]; // Orte nach dem Zeitschritt in x- und y-Richtung float Kraft_x[102] [102]; // Kraftmatrix für alle Wechselwirkungen zwischen allen Massen float Kraft_y[102] [102]; // Kraftmatrix für alle Wechselwirkungen zwischen allen Massen float m[102]; // Masse der Objekte // Hinweis: Zentralkörper 1 = Index 0, Sterne Galaxie 1 = Index 1 bis n // Zentralkörper 2 = Index n+1, Sterne Galaxie 2 = Index n+2 bis 2n+1 // =========================================================================== float Force_x,Force_y; // die auf das Objekt wirkende Kraft in x- und y-Richtung float delta_t, t, time_step; // Zeitschrittweite und aktuelle Zeit bzw. Zeitdauer für eine komplette Berechnung float Vergroesserung; // Vergrößerungsfaktor bei der grafischen Darstellung int n; // Anzahl der Objekte ohne Zentralkörper und ohne schwarzes Loch. n muss durch 4 teilbar sein! int zaehler, i, j; // Zählvariable const float Pi = 3.141592653589; const float rad = Pi / 180.0; const int Pin_continue = 6; const int Pin_fast = 5; const int Pin_slow = 4; const int Pin_zoom_in = 3; const int Pin_zoom_out = 2; int Pin_value = A0; int sensorValue; // ================= // == SETUP == // ================= void setup() { Serial.begin(9600); // Init serial interface pinMode(Pin_continue, INPUT); pinMode(Pin_fast, INPUT); pinMode(Pin_slow, INPUT); pinMode(Pin_zoom_in, INPUT); pinMode(Pin_zoom_out, INPUT); // Setup the LCD myGLCD.InitLCD(); myGLCD.setFont(SmallFont); } // ================ // == LOOP == // ================ void loop() { myGLCD.clrScr(); myGLCD.setColor(255, 255, 0); myGLCD.fillRect(0, 0, 479, 13); myGLCD.setColor(0, 0, 0); myGLCD.setBackColor(255, 255, 0); myGLCD.print("Galaxy vs. Galaxy - stoppi", CENTER, 1); myGLCD.drawBitmap (10, 30, 223, 261, M51); myGLCD.setColor(255, 255, 255); myGLCD.setBackColor(0, 0, 0); myGLCD.print("Anzahl der Sterne", 250, 30); myGLCD.print("Masse Zentralkoerper 1", 250, 70); myGLCD.print("Masse Zentralkoerper 2", 250, 110); myGLCD.print("x-Position Galaxie 2", 250, 150); myGLCD.print("y-Position Galaxie 2", 250, 190); myGLCD.print("v_x Galaxie 2", 250, 230); myGLCD.print("v_y Galaxie 2", 250, 270); myGLCD.print("<Weiter>", 310, 310); delay(1000); // ====================== // === WERTEEINGABE === // ====================== while(digitalRead(Pin_continue)) { sensorValue = analogRead(Pin_value); n = map(sensorValue,0,1023,1,12); n = 4 * n; myGLCD.setColor(0,0,0); myGLCD.fillRect(260,50,350,60); myGLCD.setColor(255, 255, 0); myGLCD.printNumI(n,260,50); //myGLCD.printNumF(n, 3, 260,50); delay(10); } delay(300); while(digitalRead(Pin_continue)) { sensorValue = analogRead(Pin_value); m[0] = map(sensorValue,0,1023,1,100); myGLCD.setColor(0,0,0); myGLCD.fillRect(260,90,350,100); myGLCD.setColor(255, 255, 0); myGLCD.printNumI(m[0],260,90); //myGLCD.printNumF(m[0], 3, 260,50); delay(10); } delay(300); while(digitalRead(Pin_continue)) { sensorValue = analogRead(Pin_value); m[n+1] = map(sensorValue,0,1023,1,100); myGLCD.setColor(0,0,0); myGLCD.fillRect(260,130,350,140); myGLCD.setColor(255, 255, 0); myGLCD.printNumI(m[n+1],260,130); //myGLCD.printNumF(m[n+1], 3, 260,130); delay(10); } delay(300); while(digitalRead(Pin_continue)) { sensorValue = analogRead(Pin_value); sx_vorher[n+1] = map(sensorValue,0,1023,50,500); myGLCD.setColor(0,0,0); myGLCD.fillRect(260,170,350,180); myGLCD.setColor(255, 255, 0); myGLCD.printNumI(sx_vorher[n+1],260,170); //myGLCD.printNumF(sx_vorher[n+1], 3, 260,170); delay(10); } delay(300); while(digitalRead(Pin_continue)) { sensorValue = analogRead(Pin_value); sy_vorher[n+1] = map(sensorValue,0,1023,-200,200); myGLCD.setColor(0,0,0); myGLCD.fillRect(260,210,350,220); myGLCD.setColor(255, 255, 0); myGLCD.printNumI(sy_vorher[n+1],260,210); //myGLCD.printNumF(sy_vorher[n+1], 0, 260,210); delay(10); } delay(300); while(digitalRead(Pin_continue)) { sensorValue = analogRead(Pin_value); vx_vorher[n+1] = map(sensorValue,0,1023,-100,0); vx_vorher[n+1] = vx_vorher[n+1] / 50.0; myGLCD.setColor(0,0,0); myGLCD.fillRect(260,250,350,260); myGLCD.setColor(255, 255, 0); //myGLCD.printNumI(vx_vorher[n+1],260,250); myGLCD.printNumF(vx_vorher[n+1], 2, 260,250); delay(10); } delay(300); while(digitalRead(Pin_continue)) { sensorValue = analogRead(Pin_value); vy_vorher[n+1] = map(sensorValue,0,1023,-100,100); vy_vorher[n+1] = vy_vorher[n+1] / 50.0; myGLCD.setColor(0,0,0); myGLCD.fillRect(260,290,350,300); myGLCD.setColor(255, 255, 0); //myGLCD.printNumI(vy_vorher[n+1],260,290); myGLCD.printNumF(vy_vorher[n+1], 2, 260,290); delay(10); } delay(300); // ====================== // === SIMULATION === // ====================== myGLCD.clrScr(); myGLCD.setColor(255, 255, 0); myGLCD.fillRect(0, 0, 479, 13); myGLCD.setColor(0, 0, 0); myGLCD.setBackColor(255, 255, 0); myGLCD.print("Galaxy vs. Galaxy - stoppi", CENTER, 1); sx_vorher[0] = 0.0; // Start-Standort des Zentralkörpers 1 sy_vorher[0] = 0.0; vx_vorher[0] = 0.0; vy_vorher[0] = 0.0; t = 0.0; delta_t = 0.2; Vergroesserung = 1; // Stern-Initialisierung // ===================== for (i = 1; i <= n; i++) { m[i] = 0.01; // Masse eines Sterns der ersten Galaxy } for (i = n+2; i <= 2*n+1; i++) { m[i] = 0.01; // Masse eines Sterns der zweiten Galaxy } zaehler = 0; for (j = 1; j <= 4; j++) // Festlegung der Stern-Startorte und Geschwindigkeiten der Galaxie 1 { for (i = 0; i < n/4; i++) { zaehler = zaehler + 1; sx_vorher[zaehler] = 10.0 * j * cos(rad * 360.0 * i * 4 / n); sy_vorher[zaehler] = 10.0 * j * sin(rad * 360.0 * i * 4 / n); vx_vorher[zaehler] = -sin(rad * 360 * i * 4 / n) * sqrt(m[0] / sqrt(sx_vorher[zaehler] * sx_vorher[zaehler] + sy_vorher[zaehler] * sy_vorher[zaehler])); vy_vorher[zaehler] = cos(rad * 360 * i * 4 / n) * sqrt(m[0] / sqrt(sx_vorher[zaehler] * sx_vorher[zaehler] + sy_vorher[zaehler] * sy_vorher[zaehler])); } } zaehler = n+1; for (j = 1; j <= 4; j++) // Festlegung der Stern-Startorte und Geschwindigkeiten der Galaxie 2 { for (i = 0; i < n/4; i++) { zaehler = zaehler + 1; sx_vorher[zaehler] = 10.0 * j * cos(rad * 360.0 * i * 4 / n); sy_vorher[zaehler] = 10.0 * j * sin(rad * 360.0 * i * 4 / n); vx_vorher[zaehler] = -sin(rad * 360 * i * 4 / n) * sqrt(m[n+1] / sqrt(sx_vorher[zaehler] * sx_vorher[zaehler] + sy_vorher[zaehler] * sy_vorher[zaehler])) + vx_vorher[n+1]; vy_vorher[zaehler] = cos(rad * 360 * i * 4 / n) * sqrt(m[n+1] / sqrt(sx_vorher[zaehler] * sx_vorher[zaehler] + sy_vorher[zaehler] * sy_vorher[zaehler])) + vy_vorher[n+1]; sx_vorher[zaehler] = sx_vorher[zaehler] + sx_vorher[n+1]; sy_vorher[zaehler] = sy_vorher[zaehler] + sy_vorher[n+1]; } } for(i = 0; i <= 2*n+1; i++) // Kraft auf sich selbst ist 0 { Kraft_x [i] [i] = 0; Kraft_y [i] [i] = 0; } myGLCD.setBackColor(0, 0, 0); myGLCD.setColor(255, 255, 0); myGLCD.print("dt: ", 40, 310); myGLCD.setColor(0,0,0); myGLCD.fillRect(70,310,120,320); myGLCD.setColor(255, 255, 0); myGLCD.printNumF(delta_t, 3, 70, 310); myGLCD.print("zoom: ", 210, 310); myGLCD.setColor(0,0,0); myGLCD.fillRect(260,310,310,320); myGLCD.setColor(255, 255, 0); myGLCD.printNumF(Vergroesserung, 3, 260, 310); myGLCD.print("<Weiter>", 380, 310); while(digitalRead(Pin_continue)) { // =================== // === Key pressed === // =================== if(digitalRead(Pin_fast)) { delta_t = delta_t * 2.0; myGLCD.setColor(0,0,0); myGLCD.fillRect(70,310,120,320); myGLCD.setColor(255, 255, 0); myGLCD.printNumF(delta_t, 3, 70,310); delay(300); } if(digitalRead(Pin_slow)) { delta_t = delta_t / 2.0; myGLCD.setColor(0,0,0); myGLCD.fillRect(70,310,120,320); myGLCD.setColor(255, 255, 0); myGLCD.printNumF(delta_t, 3, 70,310); delay(300); } if(digitalRead(Pin_zoom_in)) { myGLCD.setColor(0, 0, 0); if(abs(Vergroesserung * sx_vorher[0]) <= 240 && abs(Vergroesserung * sy_vorher[0]) <= 145) { myGLCD.drawCircle((int) 240 + Vergroesserung * sx_vorher[0], (int) 160 - Vergroesserung * sy_vorher[0], 3); } if(abs(Vergroesserung * sx_vorher[n+1]) <= 240 && abs(Vergroesserung * sy_vorher[n+1]) <= 145) { myGLCD.drawCircle((int) 240 + Vergroesserung * sx_vorher[n+1], (int) 160 - Vergroesserung * sy_vorher[n+1], 3); } for(i = 1; i <= n; i++) { if(abs(Vergroesserung * sx_vorher[i]) <= 240 && abs(Vergroesserung * sy_vorher[i]) <= 145) { myGLCD.drawPixel((int) 240 + Vergroesserung * sx_vorher[i], (int) 160 - Vergroesserung * sy_vorher[i]); } } for(i = n+2; i <= 2*n + 1; i++) { if(abs(Vergroesserung * sx_vorher[i]) <= 240 && abs(Vergroesserung * sy_vorher[i]) <= 145) { myGLCD.drawPixel((int) 240 + Vergroesserung * sx_vorher[i], (int) 160 - Vergroesserung * sy_vorher[i]); } } Vergroesserung = Vergroesserung * 2.0; myGLCD.setColor(0,0,0); myGLCD.fillRect(260,310,310,320); myGLCD.setColor(255, 255, 0); myGLCD.printNumF(Vergroesserung, 3, 260,310); delay(300); } if(digitalRead(Pin_zoom_out)) { myGLCD.setColor(0, 0, 0); if(abs(Vergroesserung * sx_vorher[0]) <= 240 && abs(Vergroesserung * sy_vorher[0]) <= 145) { myGLCD.drawCircle((int) 240 + Vergroesserung * sx_vorher[0], (int) 160 - Vergroesserung * sy_vorher[0], 3); } if(abs(Vergroesserung * sx_vorher[n+1]) <= 240 && abs(Vergroesserung * sy_vorher[n+1]) <= 145) { myGLCD.drawCircle((int) 240 + Vergroesserung * sx_vorher[n+1], (int) 160 - Vergroesserung * sy_vorher[n+1], 3); } for(i = 1; i <= n; i++) { if(abs(Vergroesserung * sx_vorher[i]) <= 240 && abs(Vergroesserung * sy_vorher[i]) <= 145) { myGLCD.drawPixel((int) 240 + Vergroesserung * sx_vorher[i], (int) 160 - Vergroesserung * sy_vorher[i]); } } for(i = n+2; i <= 2*n + 1; i++) { if(abs(Vergroesserung * sx_vorher[i]) <= 240 && abs(Vergroesserung * sy_vorher[i]) <= 145) { myGLCD.drawPixel((int) 240 + Vergroesserung * sx_vorher[i], (int) 160 - Vergroesserung * sy_vorher[i]); } } Vergroesserung = Vergroesserung / 2.0; myGLCD.setColor(0,0,0); myGLCD.fillRect(260,310,310,320); myGLCD.setColor(255, 255, 0); myGLCD.printNumF(Vergroesserung, 3, 260,310); delay(300); } // ======================================================================= // Berechnung der neuen Orte und Geschwindigkeiten mittels Euler-Verfahren // ======================================================================= //time_step = millis(); Euler(); // Alte Bildpunkte löschen // ======================= myGLCD.setColor(0, 0, 0); if(abs(Vergroesserung * sx_vorher[0]) <= 240 && abs(Vergroesserung * sy_vorher[0]) <= 145) { myGLCD.drawCircle((int) 240 + Vergroesserung * sx_vorher[0], (int) 160 - Vergroesserung * sy_vorher[0], 3); } if(abs(Vergroesserung * sx_vorher[n+1]) <= 240 && abs(Vergroesserung * sy_vorher[n+1]) <= 145) { myGLCD.drawCircle((int) 240 + Vergroesserung * sx_vorher[n+1], (int) 160 - Vergroesserung * sy_vorher[n+1], 3); } for(i = 1; i <= n; i++) { if(abs(Vergroesserung * sx_vorher[i]) <= 240 && abs(Vergroesserung * sy_vorher[i]) <= 145) { myGLCD.drawPixel((int) 240 + Vergroesserung * sx_vorher[i], (int) 160 - Vergroesserung * sy_vorher[i]); } } for(i = n+2; i <= 2*n + 1; i++) { if(abs(Vergroesserung * sx_vorher[i]) <= 240 && abs(Vergroesserung * sy_vorher[i]) <= 145) { myGLCD.drawPixel((int) 240 + Vergroesserung * sx_vorher[i], (int) 160 - Vergroesserung * sy_vorher[i]); } } // Werteübergabe und Ortsverschiebung // ================================== for (i = 0; i <= 2*n + 1; i++) { sx_vorher[i] = sx_nachher[i] - sx_nachher[0]; // Werteübergabe der Orte und Verschiebung, da Zentralkörper immer im Punkt (0,0) sy_vorher[i] = sy_nachher[i] - sy_nachher[0]; // Werteübergabe der Orte und Verschiebung, da Zentralkörper immer im Punkt (0,0) vx_vorher[i] = vx_nachher[i]; // Werteübergabe der Geschwindigkeiten vy_vorher[i] = vy_nachher[i]; // Werteübergabe der Geschwindigkeiten } // neue Orte zeichnen // ================== myGLCD.setColor(0, 255, 0); if(abs(Vergroesserung * sx_vorher[0]) <= 240 && abs(Vergroesserung * sy_vorher[0]) <= 145) { myGLCD.drawCircle((int) 240 + Vergroesserung * sx_vorher[0], (int) 160 - Vergroesserung * sy_vorher[0], 3); } for(i = 1; i <= n; i++) { if(abs(Vergroesserung * sx_vorher[i]) <= 240 && abs(Vergroesserung * sy_vorher[i]) <= 145) { myGLCD.drawPixel((int) 240 + Vergroesserung * sx_vorher[i], (int) 160 - Vergroesserung * sy_vorher[i]); } } myGLCD.setColor(255, 255, 255); if(abs(Vergroesserung * sx_vorher[n+1]) <= 240 && abs(Vergroesserung * sy_vorher[n+1]) <= 145) { myGLCD.drawCircle((int) 240 + Vergroesserung * sx_vorher[n+1], (int) 160 - Vergroesserung * sy_vorher[n+1], 3); } for(i = n+2; i <= 2*n + 1; i++) { if(abs(Vergroesserung * sx_vorher[i]) <= 240 && abs(Vergroesserung * sy_vorher[i]) <= 145) { myGLCD.drawPixel((int) 240 + Vergroesserung * sx_vorher[i], (int) 160 - Vergroesserung * sy_vorher[i]); } } t = t + delta_t; //Serial.println(millis() - time_step); //delay(500); //Serial.println(sx_nachher[2]); } } // ============================== // === UNTERPROGRAMM FORCE === // ============================== void Force() { float distance; // Distanz zwischen zwei Objekten i_Force und j_Force float einheit_x, einheit_y; // Einheitsvektor in x- bzw. y-Richtung zwischen zwei Objekten i_Force und j_Force int k_Force, l_Force; // Zählvariablen for(k_Force = 0; k_Force <= 2*n; k_Force++) { for(l_Force = k_Force + 1; l_Force <= 2*n + 1; l_Force++) { distance = sqrt((sx_vorher[l_Force] - sx_vorher[k_Force]) * (sx_vorher[l_Force] - sx_vorher[k_Force]) + (sy_vorher[l_Force] - sy_vorher[k_Force]) * (sy_vorher[l_Force] - sy_vorher[k_Force])); // Berechnung des Einheitsvektors in Richtung der Verbindungsgeraden der beiden Massen einheit_x = (1.0 / distance) * (sx_vorher[l_Force] - sx_vorher[k_Force]); einheit_y = (1.0 / distance) * (sy_vorher[l_Force] - sy_vorher[k_Force]); Kraft_x [k_Force] [l_Force] = (m[k_Force] * m[l_Force] / (distance * distance)) * einheit_x; Kraft_y [k_Force] [l_Force] = (m[k_Force] * m[l_Force] / (distance * distance)) * einheit_y; /* Serial.print("F["); Serial.print(k_Force); Serial.print(","); Serial.print(l_Force); Serial.print("] = "); Serial.print(Kraft_x [k_Force] [l_Force]); Serial.print(" "); Serial.println(Kraft_y [k_Force] [l_Force]); delay(500); */ Kraft_x [l_Force] [k_Force] = -Kraft_x [k_Force] [l_Force]; Kraft_y [l_Force] [k_Force] = -Kraft_y [k_Force] [l_Force]; } } } // ===================================== // == UNTERPROGRAMM EULER-Verfahren == // ===================================== void Euler() { int i_Euler, j_Euler; // Zählvariablen Force(); for (i_Euler = 0; i_Euler <= 2*n + 1; i_Euler++) { Force_x = 0; Force_y = 0; for (j_Euler = 0; j_Euler <= 2*n + 1; j_Euler++) { Force_x = Force_x + Kraft_x [i_Euler] [j_Euler]; Force_y = Force_y + Kraft_y [i_Euler] [j_Euler]; } vx_nachher[i_Euler] = vx_vorher[i_Euler] + delta_t * (1.0 / m[i_Euler]) * Force_x; vy_nachher[i_Euler] = vy_vorher[i_Euler] + delta_t * (1.0 / m[i_Euler]) * Force_y; sx_nachher[i_Euler] = sx_vorher[i_Euler] + delta_t * 0.5 * (vx_vorher[i_Euler] + vx_nachher[i_Euler]); sy_nachher[i_Euler] = sy_vorher[i_Euler] + delta_t * 0.5 * (vy_vorher[i_Euler] + vy_nachher[i_Euler]); } } |
Bilddatei der Galaxie M51: M51
Ein abschließendes Wort noch zur doch recht bescheidenen Anzahl an Sternen. Leider lässt der Speicher des Arduino Due keine allzu große Anzahl an Sternen zu. Im Fall Galaxy vs. black hole sind es max. 80 Sterne, im Fall Galaxy vs. Galaxy max. je 48 Sterne. Der Grund für diese Limitierung besteht darin, dass es bei n gravitativ wechselwirkenden Objekten insgesamt n·(n–1) Wechselwirkungen gibt. Man muss aber zum Glück nur die Hälfte dieser Wechselwirkungen ausrechnen, da erstens die Kraft auf sich selbst ja 0 ist für alle Objekte und zudem die Gravitationskraft ja symmetrisch ist. Die Kraft des i-ten Objekts auf das j-te Objekt ist die negative Kraft des j-ten Objekts auf das i-te. Durch diese Symmetrie verbleiben bei n Objekten also „nur“ noch ½·n·(n–1) zu berechnende Wechselwirkungen. Grob gesprochen wächst aber der notwendige Speicher und auch die Rechenzeit mit n² stark an.

Hier noch das Youtube-Video:
Venustransit und Merkurtransit
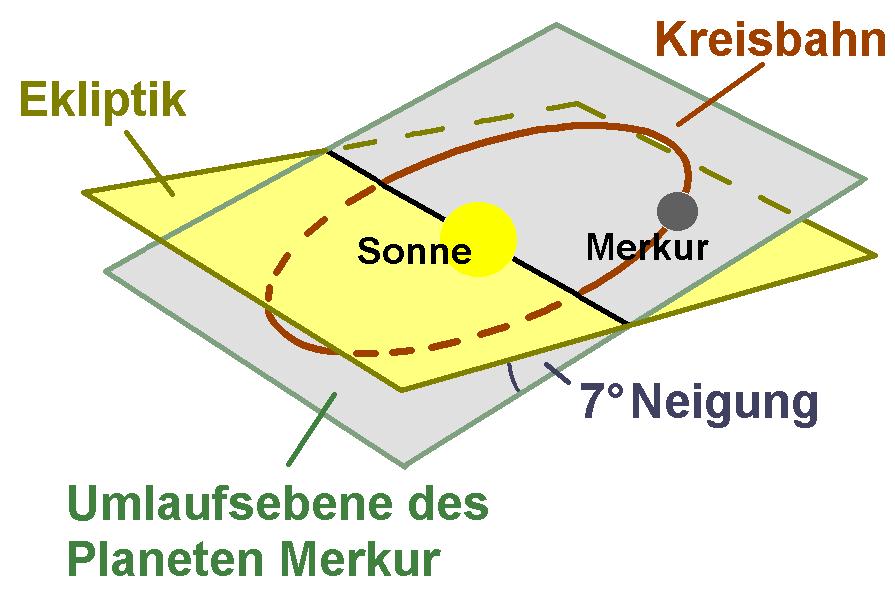
Bei dieser Simulation geht es um die Stellung der inneren Planeten Merkur und Venus bei einer sog. unteren Konjunktion. Dabei befindet sich der jeweilige Planet zwischen Sonne und Erde. Jetzt könnte man meinen, dass Merkur bzw. Venus bei einer jeden unteren Konjunktion von der Erde aus betrachtet vor der Sonnenscheibe vorbeiwandert. Dies ist aber nicht der Fall, da die Umlaufsebenen der Planeten „leicht“ unterschiedich sind. Daher ist es viel wahrscheinlicher, dass Merkur bzw. Venus bei einer unteren Konjunktion oberhalb oder unterhalb der Sonne vorbeizieht. Die Umlaufsebene des Planeten Merkur ist zum Beispiel um 7° gegenüber der Umlaufsebene der Erde (= Ekliptik) geneigt!
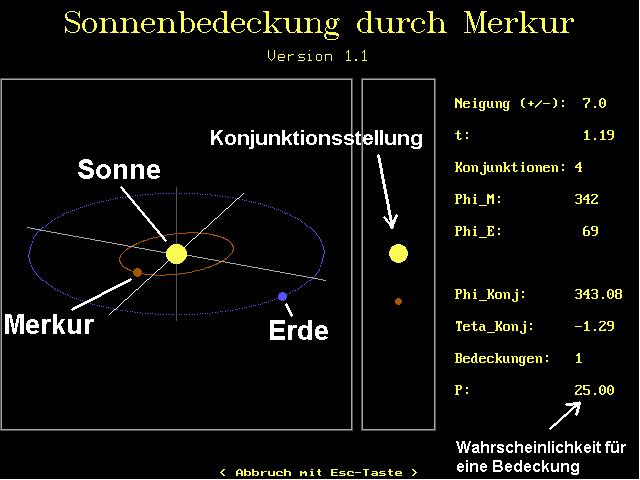
Ich habe weiters untersucht, ob die unteren Konjunktionen bei allen Positionswinkeln der Erde in etwa gleich wahrscheinlich sind. Bei 15000 unteren Konjunktionen erhielt ich folgende (Gleich)Verteilung:
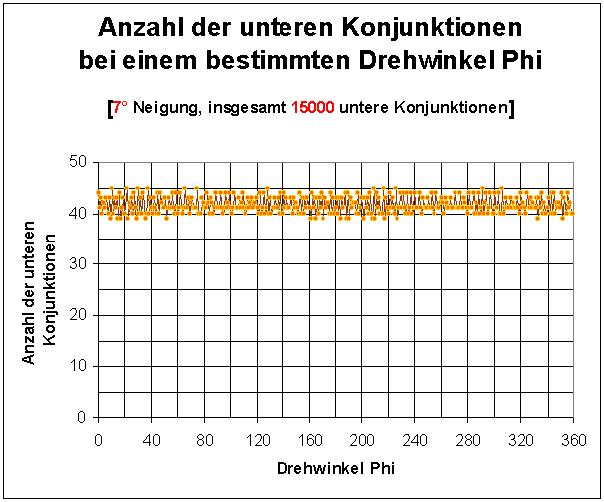
Mit diesem Ergebnis lässt sich dann die durchschnittliche Häufigkeit eines Merkur- oder Venustransits berechnen. Die Sonne besitzt von der Erde aus betrachtet einen Winkeldurchmesser von ca. 0.5° = 30 Bogenminuten. Merkur wandert bei einer unteren Konjunktion maximal um ca. 4.4° oberhalb bzw. unterhalb der Sonne vorüber (siehe untere Abbildung). Wenn nun alle Positionswinkel bei der eine untere Konjunktion stattfindet gleich wahrscheinlich sind, so gilt für die Wahrscheinlichkeit eines Merkurtransits:
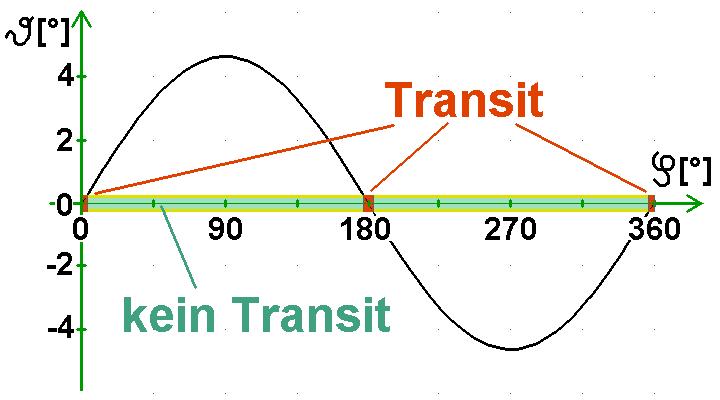
P_Merkurtransit = günstige Positionswinkel/ mögliche Positionswinkel = 4 · 3.257° / 360° = 0.0362 = 3.62%.
Eine untere Konjunktion des Planeten Merkur findet ca. alle 116 Tage statt. Wenn nur 3.59% aller unteren Konjunktionen zu einem Merkurtransit führen, muss man im Schnitt 116/0.0362 = 3204 Tage auf einen Merkurtransit warten. Dies sind 8.78 Jahre. Laut Internet kommt es insgesamt ca. 13-mal pro Jahrhundert zu einem Merkurdurchgang, was also einem durchschnittlichen Abstand zwischen 2 Merkurtransiten von 100/13 = 7.69 Jahren entspricht. Beide Werte liegen nicht allzuweit voneinander entfernt…
Venushelligkeit

Die Konjunktion der Planeten Venus und Mars (ca. in der Bildmitte) im Jahr 2015
Die scheinbare Helligkeit der Venus variiert recht stark und besitzt maximal einen Wert von -4.4 mag (lat. magnitudo für Größenklasse). Wovon hängt deren scheinbare Helligkeit, also von der Erde aus betrachtet, ab? Zum einen einmal sicher vom Abstand Erde-Venus. Die Lichtintensität einer punktförmigen Lichtquelle nimmt ja nach dem Abstandsgesetz 1/r² ab. Dies kann man auf die Venus übertragen. Demnach müsste deren Helligkeit in der unteren Konjunktion (Abstand Erde-Venus ist minimal) am größten sein. Dies ist aber nicht der Fall. Grund sind die unterschiedlichen Phasen der Venus. In der unteren Konjunktion beträgt der von der Erde aus sichtbare beleuchtete Teil der Venusoberfläche nahezu 0%. Daher wird/ist die Venus in der unteren Konjunktion zumeist unsichtbar. Die größtmögliche Phase von 100% besitzt die Venus in der oberen Konjunktion, also von der Erde aus betrachtet hinter der Sonne. In dieser Position besitzt aber die Venus zugleich auch den größten Abstand zur Erde. Daher wird das Helligkeitsmaximum irgendwo zwischen oberer und unterer Konjunktion liegen.
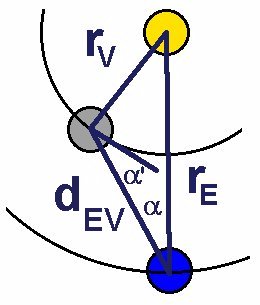
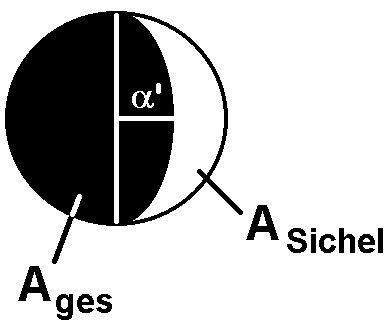

Mit meiner Simulation habe ich für alle Stellungen Erde-Sonne-Venus die beleuchtete Fläche (Phase) und den Abstand Erde-Venus berechnet und daraus deren Helligkeit abgeleitet.
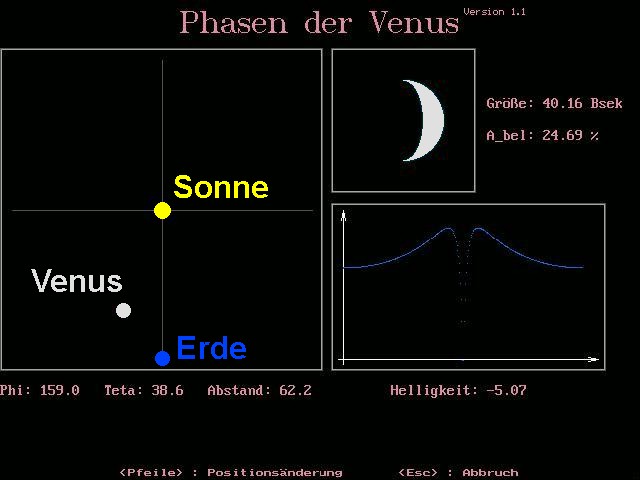
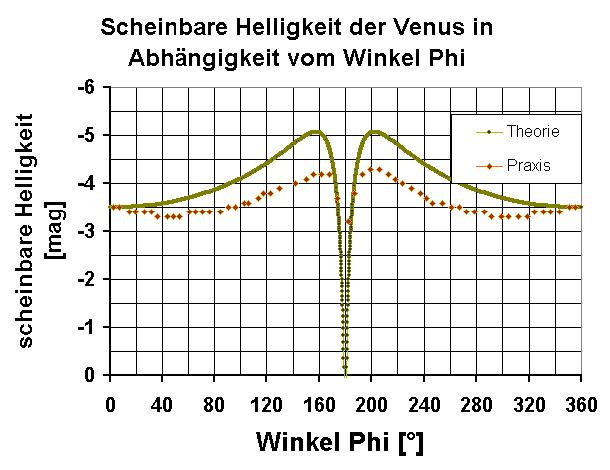
Wie man anhand des Graphen erkennen kann, beträgt der Positionswinkel der Venus bei ihrer größten scheinbaren Helligkeit rund 160°. Die Erde befindet sich fix bei einem Positionswinkel von 180°. Dies deckt sich recht gut mit dem praktischen/echten Helligkeitsverlauf…

