Spannungsdoppelbrechung
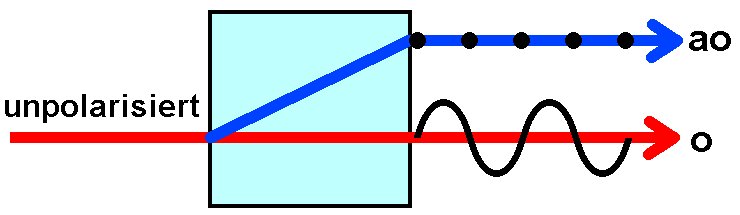
Bei mechanischer Belastung zeigen bestimmte Materialien doppelbrechende Eigenschaften, die sog. Spannungsdoppelbrechung. Unter Doppelbrechung versteht man die Fähigkeit optisch anisotroper Medien, ein Lichtbündel in zwei senkrecht zueinander polarisierte Teilbündel zu trennen. Diese beiden Teilbündel nennt man ordentlicher (o) und außerordentlicher (ao) Strahl. Die Ursache dieses Effekts liegt im unterschiedlichen Brechungsindex n0 und na0 in Abhängigkeit von der Ausbreitungsrichtung des Lichts.
In optisch isotropen Medien (isotrop = keine Richtung ist ausgezeichnet) breitet sich Licht nach allen Richtungen mit gleicher Geschwindigkeit cMedium = cVakuum / Brechungsindex n aus. Die von einer punktförmigen Lichtquelle ausgehenden Wellenflächen sind also Kugelflächen bzw. 2-dimensional betrachtet Kreise.
In optisch anisotropen Medien (anisotrop = eine Eigenschaft hängt von der Richtung ab), das sind eben doppelbrechende Medien, spaltet sich das Licht in zwei Anteile auf, welche beide linear polarisiert sind mit senkrecht zueinander orientierten Schwingungsebenen. Diese beiden Anteile nennt man wie oben schon erwähnt ordentlicher und außerordentlicher Strahl. Der ordentliche Strahl breitet sich isotrop aus, der außerordentliche anisotrop, d.h. in verschiedenen Richtungen verschieden schnell. Die von einer punktförmigen Lichtquelle ausgehenden Wellenflächen sind dann beim außerordentlichen Strahl Rotationsellipsoide bzw. 2-dimensional betrachtet Ellipsen. Entlang der optischen Achse (o. A.) stimmen die Geschwindigkeiten von ordentlichen und außerordentlichen Strahl überein. Dies bedeutet, dass sich Kreis und Ellipse auf der optischen Achse berühren. Hier ein Beispiel für einen einachsig negativen Kristall (cao > co, d.h. nao < no):
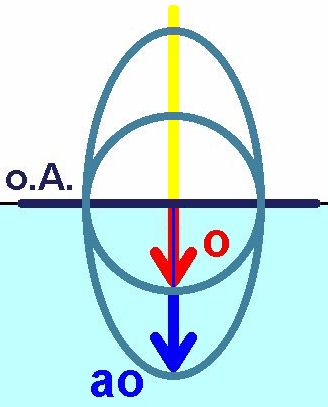
Ist der doppelbrechende Kristall so geschnitten, dass sich die optische Achse in der Schnittebene des Kristalls befindet (siehe Abbildung oben), so kommt es bei senkrechten Lichteinfall zu keiner Richtungsaufspaltung von ordentlichen und außerordentlichen Strahl. Wie aber dargestellt, ist der außerordentliche Strahl konkret schneller als der ordentliche. Am Ende des Kristalls überlagern sich dann wieder der außerordentliche und ordentliche Strahl. Je nach Länge des Kristalls kommt es aber bei der Zusammenführung zu unterschiedlichen Phasenverschiebungen. Beträgt die Phasenverschiebung etwa 90°, so entsteht aus dem in den Kristall eintretenden linear polarisierten Licht ein zirkular polarisiertes Licht. Diesen Kristall nennt man dann λ/4-Plättchen. Dazu habe ich vor mehr als 25 Jahren eine 3D-Simulation mit bewegten Wellen und allerhand Verstellmöglichkeiten in Turbo-Pascal programmiert:
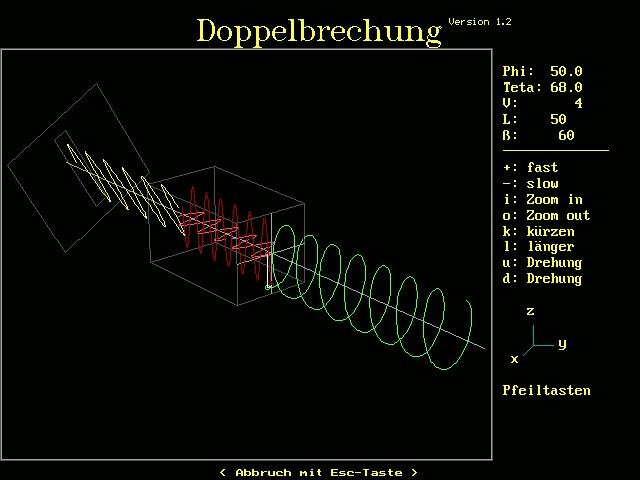

In der obigen Abbildung beträgt die Phasenverschiebung des ordentlichen und außerordentlichen Strahls genau 90°, sodass aus dem linear polarisierten Licht ein zirkular polarisiertes entsteht.
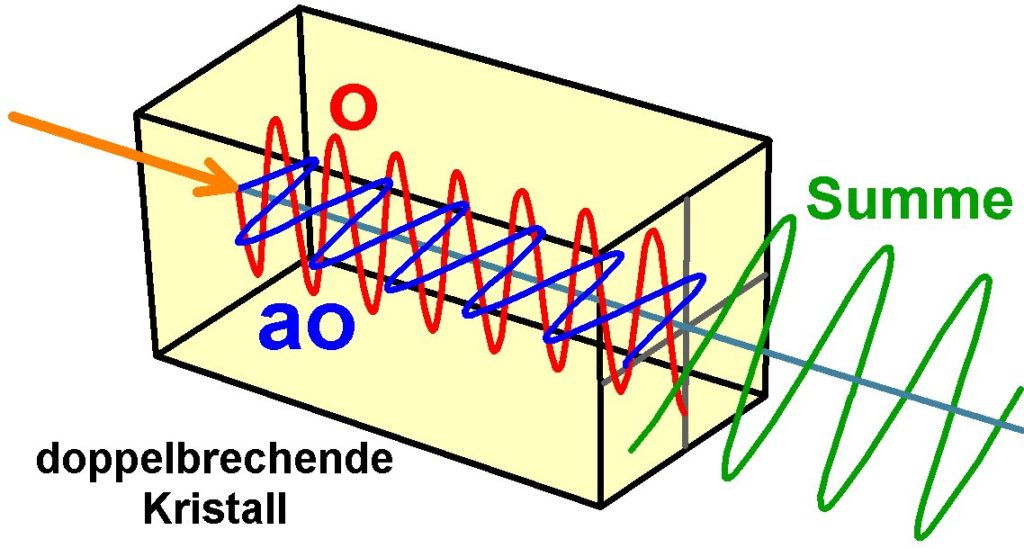
In diesem abgebildeten Fall beträgt die Phasenverschiebung zufälligerweise genau 180°. Daher verlässt auch wieder linear polarisiertes Licht den Kristall.
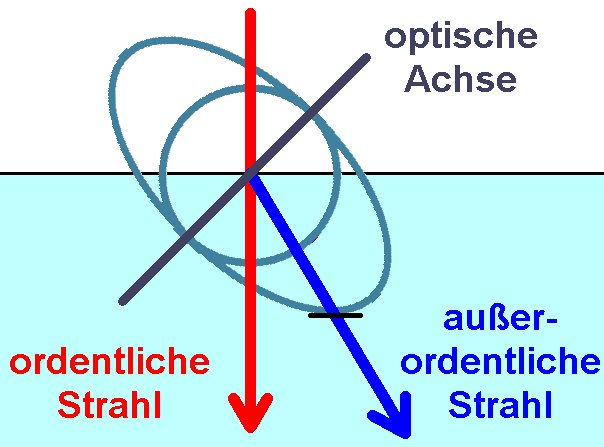
Ist der Kristall hingegen anders geschnitten, sodass die optische Achse zum Beispiel schräg zur Schnittebene des Kristalls liegt (siehe Abbildung oben), so kommt es auch bei senkrechten Lichteinfall zur einer Richtungsaufspaltung von ordentlichen und außerordentlichen Strahl. Der ordentliche Strahl verhält sich so wie erwartet, d.h. für ihn gilt das Brechungsgesetz nach Snellius. Für den außerordentlichen Strahl gilt dieses nicht mehr. Dies ergibt dann das für doppelbrechende Kristalle (z.B. Calcit, auch Kalkspat oder Doppelspat genannt) gewohnte Bild einer doppelten Schrift. Mit einem Polarisationsfilter lässt sich zum Beispiel immer jeweils eine Schrift des Doppelspats ausblenden.


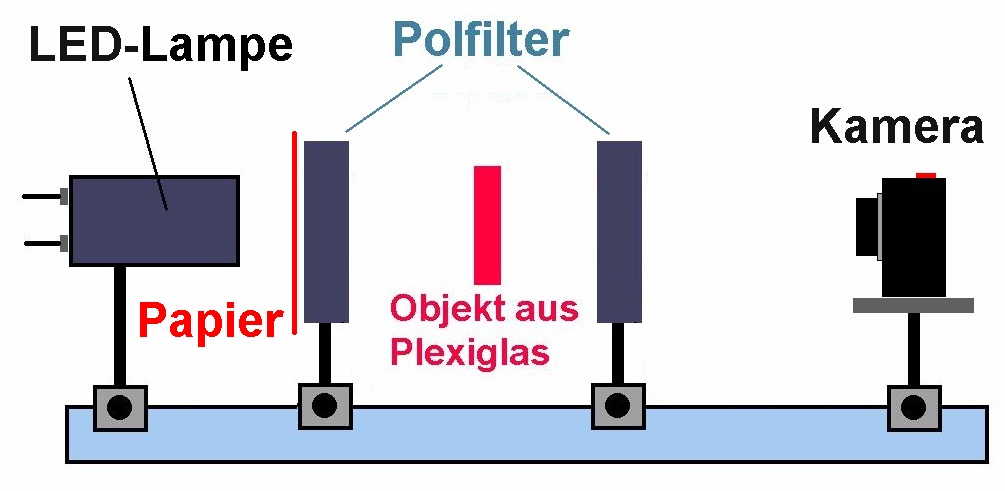
Einen für den Unterricht/das Physiklabor geeigneten Versuch stellt eben die Spannungsdoppelbrechung dar. Man benötigt hierfür nur eine helle Lichtquelle (z.B. Overhead-Projektor oder LED-Taschenlampe), 2 Polarisationsfilter (diese sind etwa bei Astro Media günstig erhältlich) und ein von den Schülern ausgeschnittenes Plexiglasmodell (z.B. Fahrradrahmen, Gabelschlüssel etc.). Befindet sich das Plexiglasmodell zwischen den beiden Polarisationsfolien und wird mechanisch etwa durch Druck mit den Fingern belastet, so erkennt man Strukturen im Modell, welche auf den jeweiligen Belastungszustand schließen lassen. Damit der Polarisator (= erste Polfilter) gleichmäßig ausgeleuchtet ist, verwende ich einfach ein gleich großes Stück Papier.









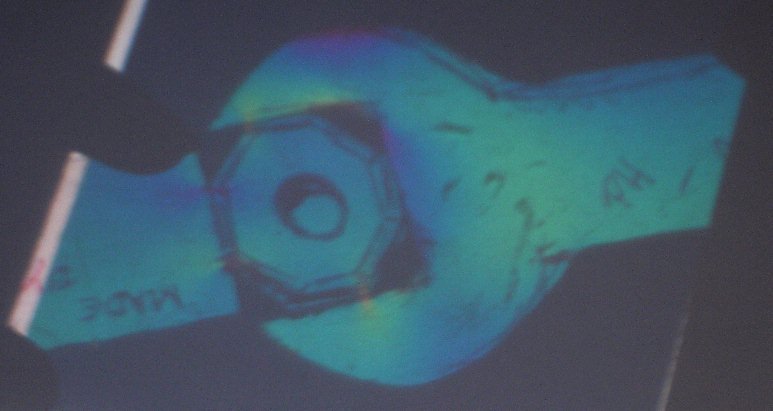
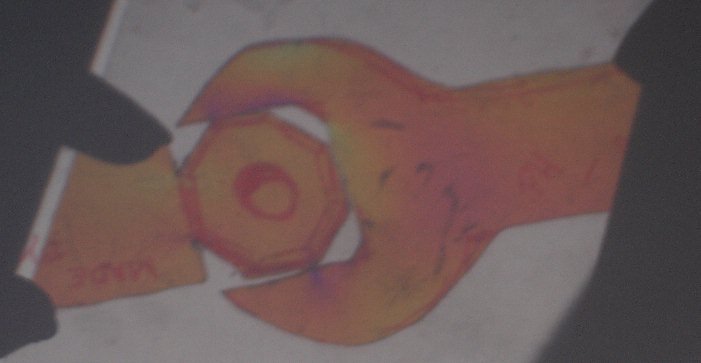
Hier einige Modelle meiner Schüler:



Polarimeter – optische Aktivität
Optisch aktive Substanzen haben die Eigenschaft, die Polarisationsebene von linear polarisierten Licht zu drehen.
 Der Drehwinkel α hängt von der Länge L der Flüssigkeitssäule ab und von der Konzentration c der optisch aktiven Flüssigkeit. Es gilt also der Zusammenhang:
Der Drehwinkel α hängt von der Länge L der Flüssigkeitssäule ab und von der Konzentration c der optisch aktiven Flüssigkeit. Es gilt also der Zusammenhang:
α = k · L · c
Die Zahl k ist ein Proportionalitätsfaktor (= spezifischer Drehwinkel), welcher für verschiedene Wellenlängen zumeist unterschiedlich ist, da nicht alle Farben gleich stark gedreht werden. Eine optisch aktive Substanz ist etwa Joghurt. Deshalb auch die Bezeichnungen links-drehend bzw. rechts-drehend.
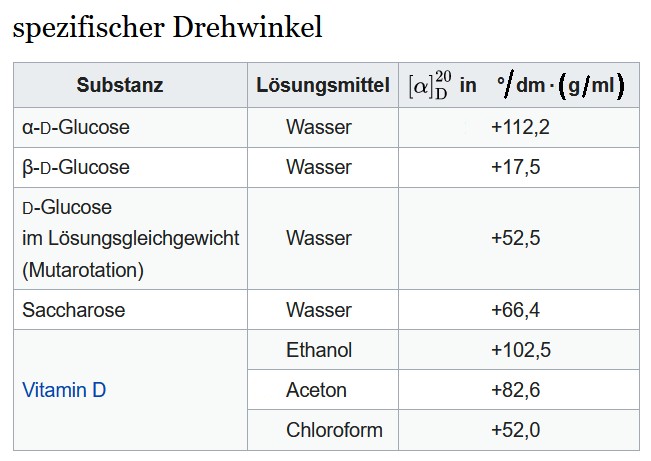
Ein Polarimeter besteht aus einer Lichtquelle (im Idealfall monochromatisch), einem Polarisationsfilter am Eingang (= Polarisator), der optisch aktiven Substanz und einem Polarisationsfilter am Ausgang (= Analysator). Ist die Substanz/Flüssigkeit nicht optisch aktiv, so erhält man die geringste Helligkeit bei senkrecht aufeinander stehenden Polarisator und Analysator. Diese Stellung ist dann die Nullstellung des Analysators.
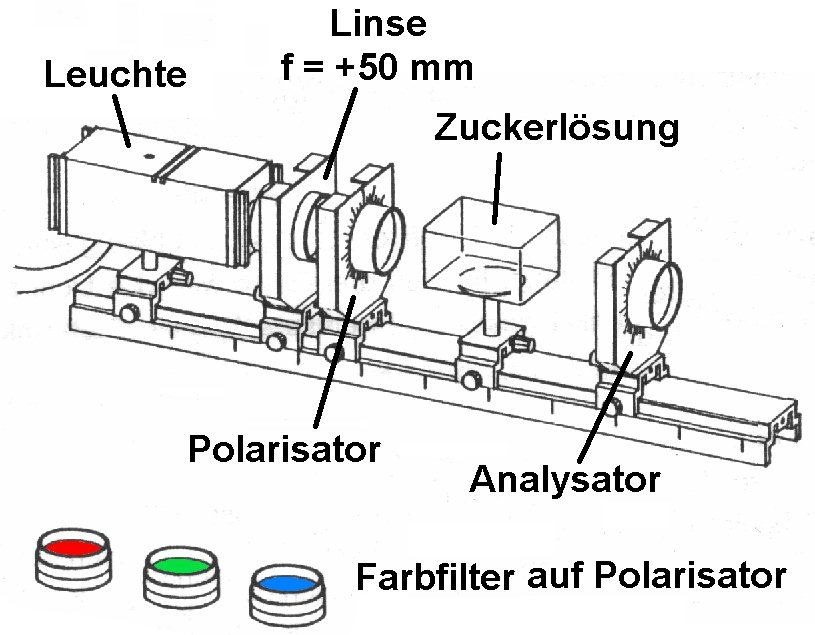
Dreht aber die Flüssigkeit die Polarisationsebene um einen Winkel α, so muss der Analysator eben um genau diesen Winkel aus der Nulllage verdreht werden, um abermals minimale Helligkeit zu erzielen. Diesen Winkel α notiert man nun bei gegebener Konzentration c bzw. kennt man die Größen α, k und L, so kann man die (unbekannte) Konzentration c ausrechnen. Um k zu kennen, muss man natürlich das Polarimeter erst mittels verschiedener bekannter Konzentrationen kalibrieren.
Von meinem Versuch “Quantenradierer” (https://stoppi-homemade-physics.de/quantenradierer/) hatte ich noch ein Stück Polarisationsfilterfolie übrig. Zwei Filterfassungen hatte ich auch zum Glück noch übrig. Diese waren Gratiszugabe bei der Bestellung mehrerer Okulare für mein Teleskop.





Die Glasküvette, welche dann mit der optisch aktiven Flüssigkeit (z.B. Zuckerlösung) gefüllt wird, habe ich im Schulmittelhandel günstig gefunden.

Was die Lichtquelle betrifft, habe ich mich noch nicht entschieden. Zur Auswahl steht meine Natrium-Niederdrucklampe oder ein Laser. Bei Verwendung des Lasers kann ich wegen der Gefahr natürlich nicht mit dem Auge durch das Polarimeter blicken, sondern muss einen Schirm verwenden. Die Lichtquelle sollte deshalb monochromatisch sein, weil wie schon erwähnt der Proportionalitätsfaktor k von der Wellenlänge abhängt. Verwende ich weißen Licht, so werden die einzelnen Farben unterschiedlich stark gedreht und ich erziele mit dem Analysator keine absolute Dunkelheit mehr.


Ich werde das Polarimeter mit meinen verschiedenen Diodenlaser betreiben. Folgende Wellenlängen stehen zur Auswahl:
- 405 nm
- 450 nm
- 520 nm
- 532 nm
- 639 nm
Damit kann ich dann die Abhängigkeit des spezifischen Drehwinkels k von der Wellenlänge wohl gut bestimmen.

Heute ist die Küvette angekommen, sodass ich den finalen Aufbau zeigen kann. Die Nullausrichtung des Analysators habe ich mit Hilfe der Sonne bewerkstelligt. Abgeglichen wird, weil das Auge hier sensibler ist, auf minimale Helligkeit.









Die Messungen mit Kristallzucker sind im Kasten und die Ergebnisse decken sich eigentlich sehr gut mit den Tabellenwerten. Je kürzer die Wellenlänge, desto größer ist die optische Aktivität bei Kristallzucker. Die folgenden Abbildungen zeigen die Drehwinkel bei 4 Würfelzucker zu je 3.6 g in rund 85 ml Wasser:








Hier nun die Messwerte: Man erkennt schön den linearen Zusammenhang zwischen der Konzentration c und dem Drehwinkel α für alle 4 verschiedenfarbigen Laser.



Trage ich die spezifischen Drehwinkel k in Abhängigkeit von der Wellenlänge λ auf und interpoliere für die Natrium-D-Linie (589 nm), so erhalte ich einen spezifischen Drehwinkel von 68 °/(dm·g/ml), was sehr gut mit dem Tabellenwert von 66.4 °/(dm·g/ml) für Saccharose übereinstimmt.

Zaubertrick mit zwei Polarisationsfolien
Für diesen Zaubertrick benötigt man lediglich zwei größere Polarisationsfolien, eine Plexiglasröhre und einen Tischtennisball o.ä.

Bei der Polarisationsfolie muss man darauf achten, dass sie erstens NICHT klebend ist und zweitens die Polarisationsrichtung parallel bzw. normal zur Seitenkante ausgerichtet ist. Bei aus China bestellten Folien war dies nämlich nicht der Fall und deren Orientierung war 45° gegenüber den Schnittkanten!


Die beiden Filter schneidet man so zurecht, dass sie die Innenseite der Röhre möglichst ohne Überlappung oder Freiraum auskleiden. Dabei aber unbedingt auf die Orientierung der Folien achten. Sie müssen nämlich wie abgebildet gekreuzt zueinander eingebaut werden:

Im mittleren Bereich hat man jetzt den Eindruck, als befände sich dort ein schwarzer Boden. Nun besorgt man sich noch einen Tischtennisball und lässt diesen wohlgemerkt erst nach Murmeln kryptischer Zaubersprüche durch das Plexiglasrohr fallen. Wie durch Zauberei kann der Ball den Boden mühelos überwinden und kommt an der anderen Seite wieder an…



Das Youtube-Video von meinen Zauberkünsten reiche ich natürlich nach…
3 Polarisationsfilter-Paradoxon
Zum obigen Zaubertrick passt sehr gut dieses Paradoxon. Man benötigt dazu nur 3 Polarisationsfilter und einen Laser. Zunächst schickt man den Laserstrahl durch einen einzelnen Polarisationsfilter, welcher horizontal ausgerichtet ist:


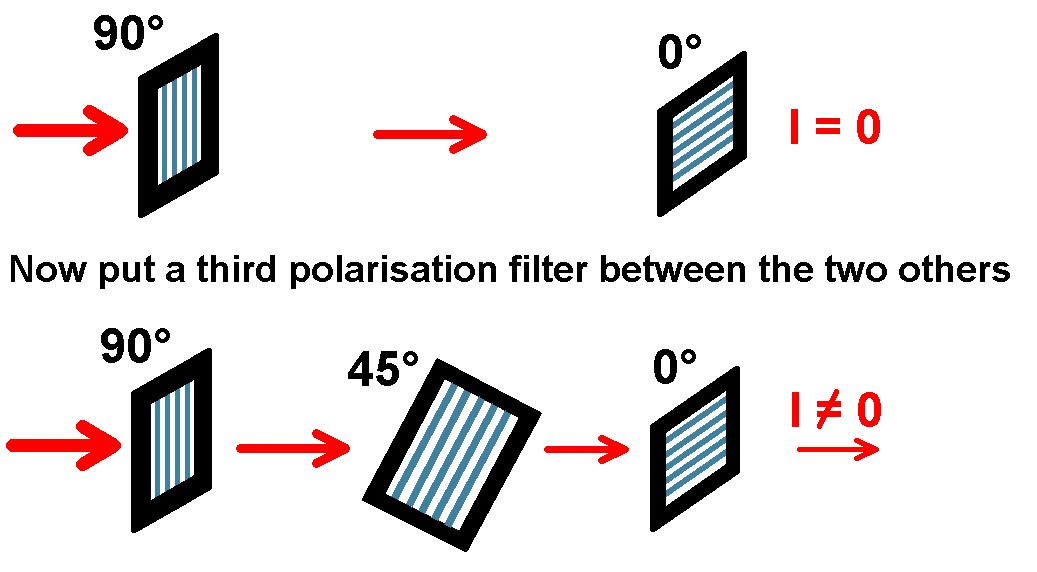
Dann postiert man einen vertikal ausgerichteten Polarisationsfilter hinter dem ersten. Der Laserstrahl verschwindet…


Und nun der Zaubertrick: Gibt man einen um 45° geneigten Polarisationsfilter zwischen die beiden anderen, so sieht man den Laser wieder auf dem Schirm:


Wie kann dies sein, dass durch einen hinzugefügten Filter die Helligkeit wieder wächst? Betrachten wir hierzu die durchgelassenen Schwingungsebenen:
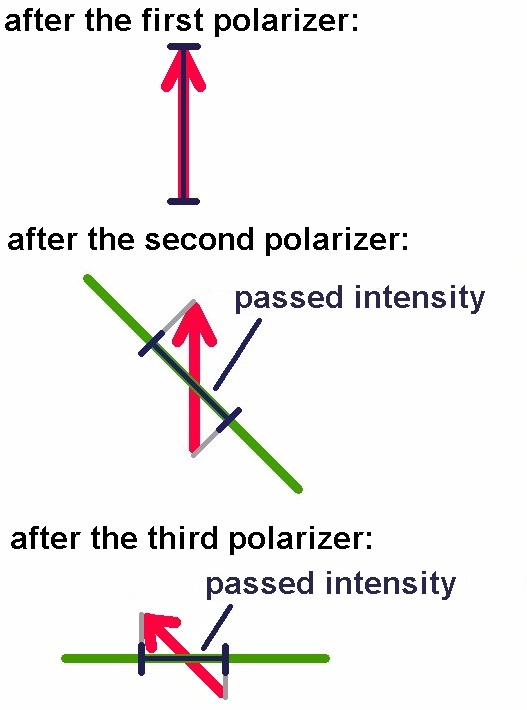
Das magische Klebeband
Einen “Zaubertrick” mit Polarisationsfolien habe ich noch auf Lager. Benötigt werden zwei Polarisationsfilter, eine Overheadfolie und Klebeband. Dieses klebt man regellos auch übereinander auf die Overheadfolie. Gibt man nun diese mit dem Klebeband zwischen zwei Polarisationsfolien, so entsteht ein wunderschönes Farbenspiel. Dies deshalb, weil die Klebefolie doppelbrechend ist und das linear polarisierte Licht des Polarisators für die einzelnen Farben in unterschiedlich polarisiertes Licht aufspaltet. Durch den Analysator dringen dann immer unterschiedliche Farben mit unterschiedlichen Intensitäten und ergeben in Summe dann dieses schöne Farbenspiel…








