Das berühmte Induktionsgesetz geht auf Michael Faraday zurück. Es besagt, dass bei einer Änderung des magnetischen Flusses (vereinfacht ausgedrückt des Magnetfelds) innerhalb einer Spule eine elektrische Spannung U induziert wird. Die Formel lautet:

Ändert sich der magnetische Fluss innerhalb der Spule nicht, wird auch keine Spannung induziert. Betrachten wir folgendes Experiment: Ein Magnet wird oberhalb einer Spule losgelassen und fällt durch die Spule hindurch. Welchen Verlauf der Induktionsspannung erwarten wir?
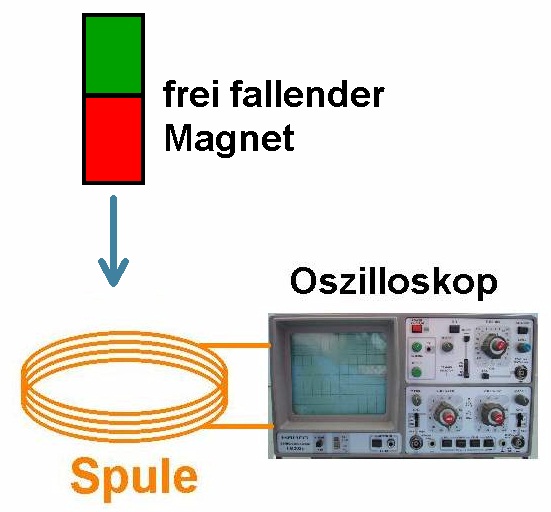
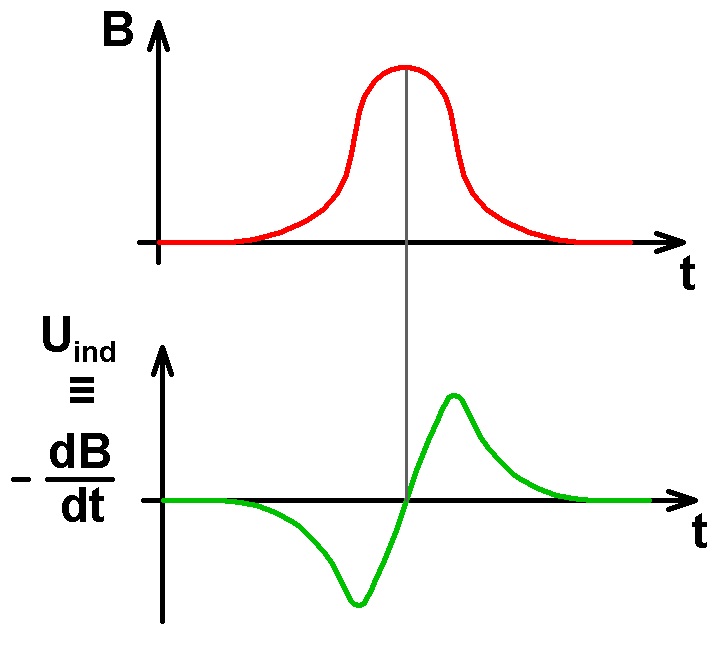
Die Flussdichte B wird wenn sich der Magnet der Spule nähert ansteigen, ein Maximum durchschreiten und dann wieder abnehmen (rote Kurve). Die Induktionsspannung Uind, welche ja proportional zur zeitlichen Änderung von B ist (≡ erste Ableitung), wird dann ungefähr den grünen Verlauf annehmen.
Dieses Experiment habe ich natürlich auch durchgeführt. Dazu habe ich ein PVC-Rohr genommen und die Verdickung an einem Ende abgeschnitten. Auf diesem etwas größeren Rohrstück habe ich dann die Spule mit n = 100 Windungen aufgewickelt.









Passende Magnete hatte ich zum Glück noch in meinem Fundus:




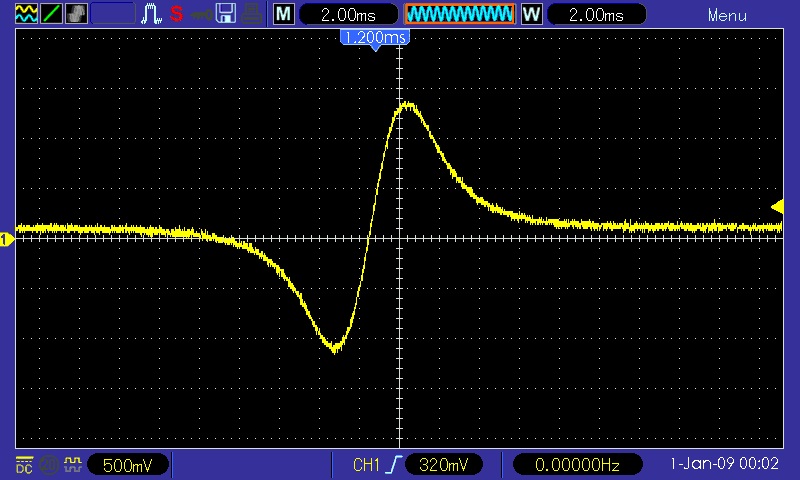
Hier nun der erhaltene Spannungsverlauf, welcher sich sehr gut mit der Erwartung deckt:
Kann man nun dieses Induktionsgesetz für etwas nutzen? Ja, man kann damit zum Beispiel die Stärke des Magneten, also seine Flussdichte B, bestimmen. Betrachten wir hierzu das Induktionsgesetz noch einmal genauer:
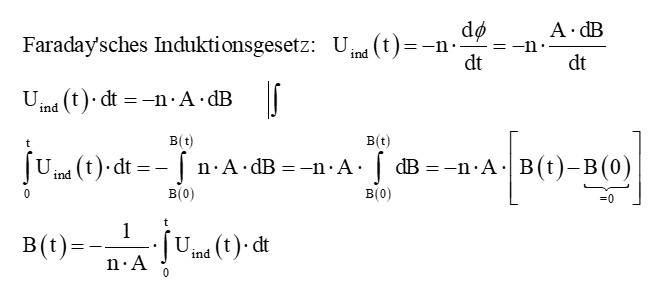
Mit dem Integral, also der Fläche unter der Uind(t)-Kurve, kann man den zeitlichen Verlauf der Flussdichte B(t) bestimmen.

Gehe ich mit dem Integral bis zur Nullstelle in der Mitte, so erhalte ich die maximale Flussdichte B0:

Lasse ich den Magneten aus unterschiedlichen Höhen durch die Spule fallen, so wird die Induktionsspannung bei schnelleren Magneten höher ausfallen, da sich dann ja das Magnetfeld schneller ändert. Die Fläche unter der Kurve bis zur ersten Nullstelle müsste dann aber nach wie vor B0 ergeben. Dies ist dadurch garantiert, dass die Zeit über die integriert wird nun kürzer ist, da der Puls nicht so lange dauert…
Heute konnte ich einige Messungen durchführen. Dabei ließ ich den Magneten einmal aus größerer Höhe fallen und dann aus geringerer. Hier die beiden erhaltenen Spannungsverläufe:


Da mein Oszilloskop über keine Integralfunktion verfügt und ich keine Lust hatte, die Kästchenteile aufzusummieren, habe ich mich für eine unkonventionelle Methode entschieden. Und zwar bestimme ich die Integrale mittels Waage. Dazu drucke ich die beiden Spannungsverläufe auf ein Blatt Papier aus und schneide die in Frage kommenden Flächen unter der Kurve aus. Das gleiche mache ich mit einer Normfläche bestehend aus konkret 9 Kästchen. Ein Kästchen besitzt ja die “Länge” 2 ms und die “Höhe” 500 mV. Die Fläche eines Kästchens entspricht also der Fläche 2 ms · 500 mV = 1 mVs. Wiege ich die 9 Kästchen ab und dividiere dann die mit der Waage erhaltene Masse durch 9, so erhalte ich die Masse von 1 mVs. Jetzt brauche ich nur noch die erhaltenen Massen der Flächen unter der Kurve durch diesen Zahlenwert dividieren und schon bekomme ich deren Fläche in mVs. 😉





Wie zu erwarten war, wiegen die beiden gesuchten Integrale gleich viel:


Hier noch die dazugehörige Rechnung: 
Die mittlere maximale Flussdichte verteilt auf die gesamte Fläche innerhalb der Spule beträgt also 0.19 T. Dies habe ich natürlich sogleich mit meinem Teslameter überprüft:




Während die Flussdichte in er Mitte des Magneten rund 0.41 T betrug, sank dieser Wert mit zunehmender Entfernung von der Mitte deutlich ab. Knapp außerhalb des Rands betrug er zum Beispiel nur noch 0.07 T. Daher passt eine mittlere Flussdichte von 0.19 T sehr gut zu diesen Messungen, Heureka… 🙂

