
Bildquelle: https://en.wikipedia.org/wiki/Wilhelm_Hallwachs
Am Beginn des 20. Jahrhunderts konnte man sich den sog. Photo- bzw. Hallwachseffekt mit Licht als Welle nicht erklären. Beim Photoeffekt beleuchtet man mit einer Lampe (UV oder mittels Filter andere Wellenlängen) eine elektrisch negativ aufgeladene Zinkplatte. Diese ist mit einem Elektroskop verbunden, welches die Ladung anzeigt.

Leuchtet man nun mit UV-Licht die Platte an, so nimmt deren elektrische Ladung rasch ab. Verwendet man hingegen Licht mit größerer Wellenlänge, so passiert gar nichts. Dies widerspricht aber den Erwartungen, wenn Licht als reine elektromagnetische Welle betrachtet wird. Welche Dinge sollte man “klassisch” betrachtet beobachten?
1.) Die Ablösung von Elektronen dürfte nicht sofort eintreten
Nehmen wir an, die Lampe mit der Leistung P = 50 W und dem Wirkungsrad η = 4 % befinde sich im Abstand r = 0.4 m zur Zinkplatte. Weiters nehmen wir an, dass ein Zinkatom eine Seitenlänge von 10^ –10 m besitzt. Damit befindet sich unter der Annahme einer quadratischen Form pro 10^ –20 m² ein Zinkatom. Die Ablösearbeit für ein Elektron betrage 2 eV.


Wie man sieht, müsste es rund 32 Sekunden dauern, bis die für die Ablösung eines Elektrons notwendige Energie erreicht wird. Dies stand wie gesagt im Widerspruch zur Beobachtung der sofortigen Ablösung.
2.) Die Entladung müsste von der Intensität des Lichts abhängen
Besitzt die Lichtquelle eine höhere Leistung P, so müsste die Entladung schneller stattfinden. Wenn auch die Leistung P eine Rolle spielt, so ist primär scheinbar die Wellenlänge/Frequenz der verwendeten Lichtquelle ausschlaggebend. Verwendet man etwa eine Infrarotlampe, so kann deren Leistung beliebig hoch sein und es werden dennoch keine Elektronen abgelöst. Erst bei Verwendung höherfrequenten Lichts kommt es zur Entladung der Zinkplatte. Dann hängt die Schnelligkeit dieser aber sehr wohl von der Intensität der Lampe ab.
3.) Klassisch betrachtet müsste eigentlich eine elektromagnetische Welle mit höherer Frequenz f sogar eine geringere Ablösung bewirken. Dies kann wie folgt hergeleitet werden:

Um den äußeren lichtelektrischen Effekt also erklären zu können, bedurfte es eines komplett neuen Ansatzes. Und dieser Ansatz wurde vom deutschen Physiker Max Planck (1858 – 1947) auch getätigt.

Bildquelle: https://de.wikipedia.org/wiki/Max_Planck#/media/Datei:Max_Planck_(1858-1947).jpg
Sein fundamental neuer Ansatz läutete quasi den Beginn der Quantenphysik ein. Er postulierte, dass Licht nur in diskreten Energieportionen existieren kann. Diese Energieportionen E hängen mit der Frequenz des Lichts wie folgt zusammen:
E = h · f mit dem Planckschen Wirkungsquantum h = 6.63 · 10^ –34 Js.
Verwendet man also eine Lichtquelle mit einer bestimmten Frequenz f, so tritt die Lichtenergie ausschließlich in Portionen h·f auf. Dies ebnete den Weg für die Interpretation von Licht als Teilchen, den sog. Photonen.
Warum konnte man mit dieser Teilchentheorie nun den Photoeffekt so elegant erklären? Nun für die Ablöse der Elektronen ist eine bestimmte Energie E_ion notwendig. Besitzt nun die Lichtquelle eine Frequenz f mit h·f < E_ion, so reicht die Energie der Photonen nicht aus, um die Elektronen abzulösen. Auch eine Steigerung der Intensität hätte keinen Einfluss, da sich ja dadurch an der einzelnen Energie der Photonen nichts ändert. Erst für h·f > E_ion ist das Licht/sind die Lichtteilchen imstande, die Elektronen abzulösen. Genau diese Beobachtung machte man ja.
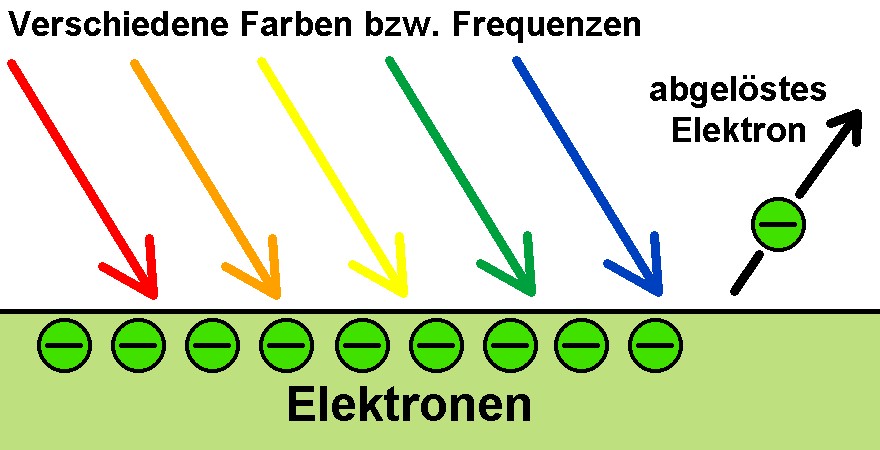

Hundert Opel sind langsamer als ein Ferrari
Es gilt in diesem Zusammenhang zu erwähnen, dass der wohl bekannteste Physiker Albert Einstein genau für seine Arbeiten zum äußeren lichtelektrischen Effekt und nicht etwa für seine Relativitätstheorien den Nobelpreis für Physik 1921 zugesprochen bekam!
Experiment 1:
Der klassische Versuch zum äußeren lichtelektrischen Effekt (Photoeffekt oder auch Hallwachs-Effekt genannt) bedient sich einer Zinkplatte, eines Elektroskops zum Nachweis der elektrischen Ladungen und verschiedener Lichtquellen, darunter auch eine UV-C Lichtquelle.
Ein Elektroskop lässt sich ganz einfach selbst basteln. Man benötigt lediglich ein Glas mit Plastikdeckel, etwas Draht, ein Stück Aluminiumfolie und eine Metallplatte zum Aufbringen der Ladungen.




Die restlichen Materialien für dieses Experiment erhält man u.a. auf aliexpress oder ebay.

Betrachten wir die Dinge einmal genauer: Die Austrittsarbeit für ein überschüssiges Elektron von Zink beträgt 4.34 eV. Die mittels Photonen zugeführte Lichtenergie berechnet sich nach Max Planck ja mittels der Beziehung E = h · f = h · c / λ. Daraus lässt sich die maximale Wellenlänge, welche gerade noch zur Ablösung der Elektronen reicht, berechnen:
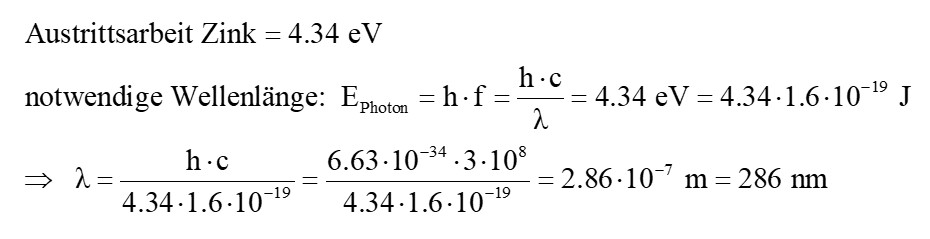
Die Wellenlänge der Photonen muss also ≤ 286 nm sein. Dies liegt bereits an der Grenze zum UV-C Bereich. Eine entsprechende Lampe mit λ = 253.7 nm erhält man ebenfalls auf aliexpress:

Mittlerweile sind einige Sachen aus China eingetroffen: Die Stäbe zum Übertragen der Ladungen, ein Fell und ein Stoffstück und dann noch die UV-C Lampe. Sie gibt ein schön gefärbtes Licht ab, wenngleich man ungeschützt sich nicht lange der UV-Strahlung aussetzen sollte!



Auch die Zinkplatte ist mittlerweile eingetroffen und ich konnte einen ersten erfolgreichen Versuch starten. Am geeignetsten hat sich die Kombination durchsichtiger Glas/Kunststoffstab + Pullover herausgestellt. Mit der UV-C Lampe erfolgt die vollständige Entladung binnen einer Sekunde. Mit der 365 nm-UV-Taschenlampe geschieht hingegen wie zu erwarten war nichts.


Experiment 2:
Dieser äußere, lichtelektrische Effekt kann auch mittels einer Photozelle (= alte Röhre etwa zur Messung der Lichtintensität) sehr einfach nachgestellt werden. Zusätzlich kann damit neben der Ablösearbeit E_ion auch das Plancksche Wirkungsquantum h bestimmt werden.


Photozellen erhält man relativ günstig auf ebay. Ich habe für ein Stück rund 15–20 Euro bezahlt. Neben der Photozelle werden noch LEDs unterschiedlicher Farbe, eine 1.5 V Batterie, ein Potentiometer und ein Multimeter benötigt. Normalerweise ist jene großflächige Elektrode, von der die Elektronen abgelöst werden, mit der Kathode verbunden. Man spricht deshalb auch von der sog. Photokathode. In unserem Fall wird diese aber mit dem Pluspol der variablen Spannung verbunden. Wie erfolgt nun eine Messung? Man beleuchtet die Photokathode mit einer LED bestimmter Farbe/Frequenz. Mittels Potentiometer stellt man zunächst eine Gegenspannung U = 0 V ein. Die von den Photonen an die Elektronen übergebene Energie reicht nun aus, dass diese die Kathode erreichen können und für einen (kleinen) Strom sorgen.

Danach vergrößert man stetig die Gegenspannung. Die abgelösten Elektronen mit der kinetischen Energie E_kin tun sich immer schwerer gegen die steigende Gegenspannung anzukämpfen um zur Kathode zu gelangen. Um die Gegenspannung U zu überwinden, ist ja die Energie U = E/q ⇒ E = U·q = U·e notwendig.
Ist nun die Gegenspannung U so groß, dass der Anodenstrom auf 0 sinkt, so entspricht die kinetische Energie der abgelösten Elektronen exakt der durch die Gegenspannung aufzuwendenden Arbeit. Es gilt für diesen Fall (I = 0):
E_kin = U·e
Energetisch muss also folgende Gleichung gelten: Photonenenergie h·f = Ablöseenergie E_ion + E_kin = E_ion + U·e
Löst man diese Gleichung nach U auf erhält man: U(f) = (h/e)·f – E_ion/e

Trägt man also die notwendige Gegenspannung U in Abhängigkeit von der Lichtfrequenz f auf, müsste man eine Gerade erhalten, aus deren Anstieg k das Plancksche Wirkungsquantum h und aus deren Ordinatenabschnitt d die Ionisierungsenergie ermittelt werden kann.









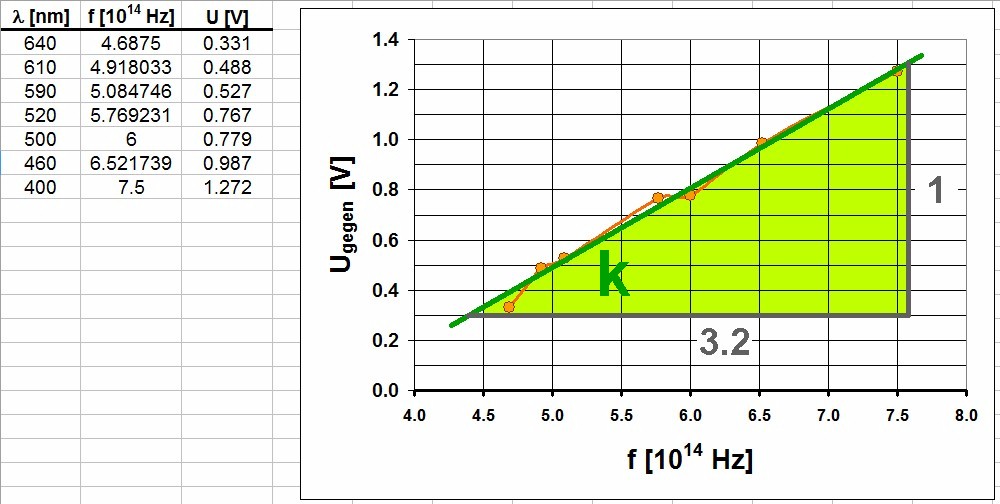
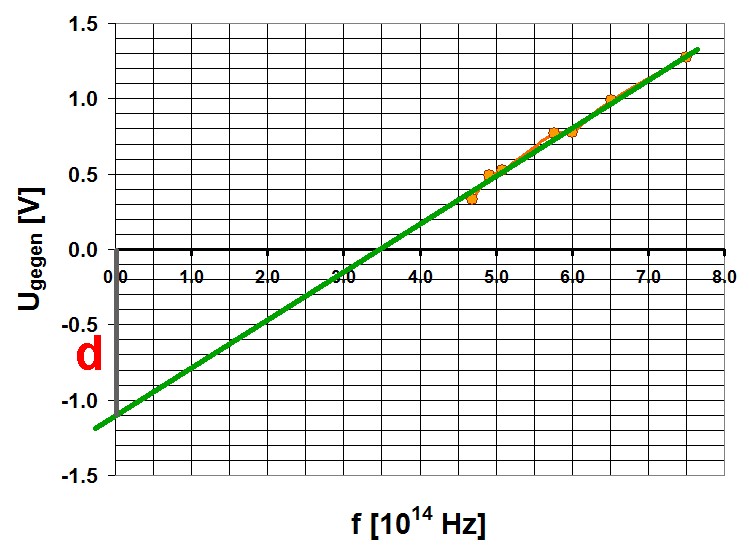

Die Ablöseenergie/Ionisierungsenergie der verwendeten Photozelle beträgt also konkret 1.1 eV. Das Plancksche Wirkungsquantum konnte zu 5 · 10^ –34 Js bestimmt werden. Der richtige Wert liegt bei 6.63 · 10^ –34 Js.

