Einzelatome oder ein dünnes Gas besitzen nur diskrete Energieniveaus für die Elektronen. Das Termschema besitzt dann also nur einzelne, diskrete Stufen. Bei Festkörper bilden sich anstelle der einzelnen Sprossen Bänder aus. Das höchste, voll mit Elektronen besetzte Band nennt man Valenzband (VB). Jenes darüber ist das sog. Leitungsband (LB).
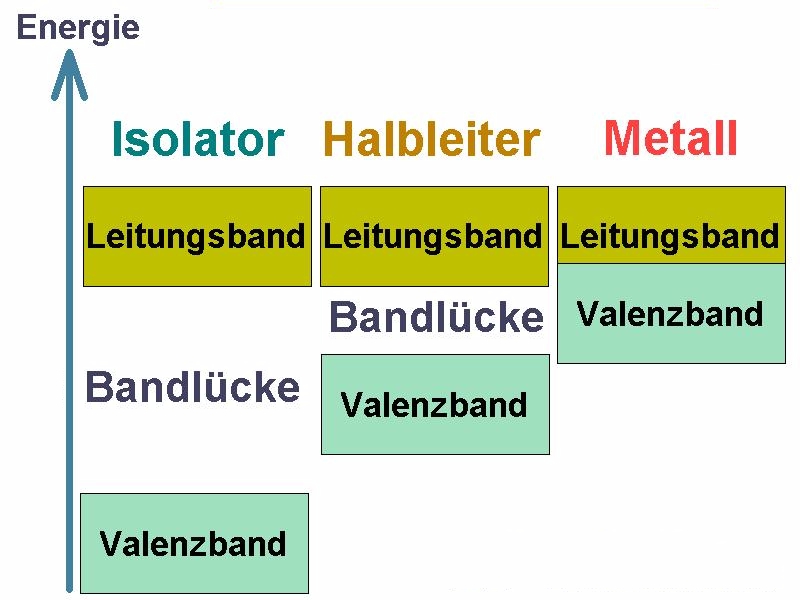
Bei Isolatoren ist das Leitungsband leer und die Lücke (der sog. Bandabstand) zwischen VB und LB groß. Daher leiten Isolatoren den elektrischen Strom nicht. Bei Halbleitern ist zumindest bei tiefen Temperaturen das Leitungsband auch leer. Der Bandabstand ist aber geringer als bei den Isolatoren. Bei Metallen überlappen VB und LB und es befinden sich selbst bei niedrigen Temperaturen zahlreiche Elektronen im LB. Diese Elektronen tragen dann zur guten Leitfähigkeit der Metalle bei.
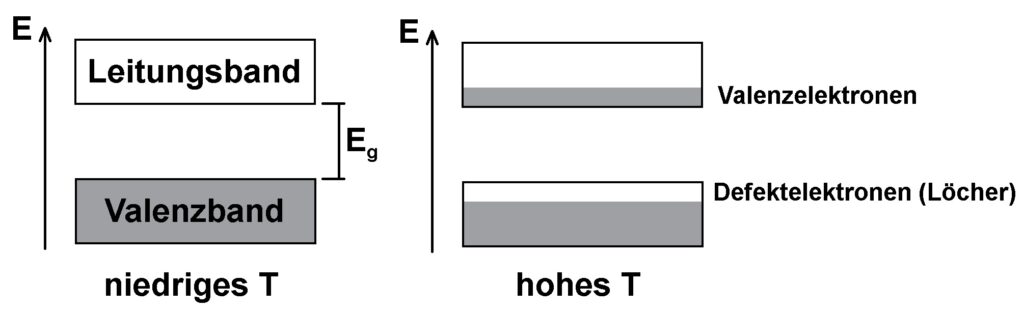
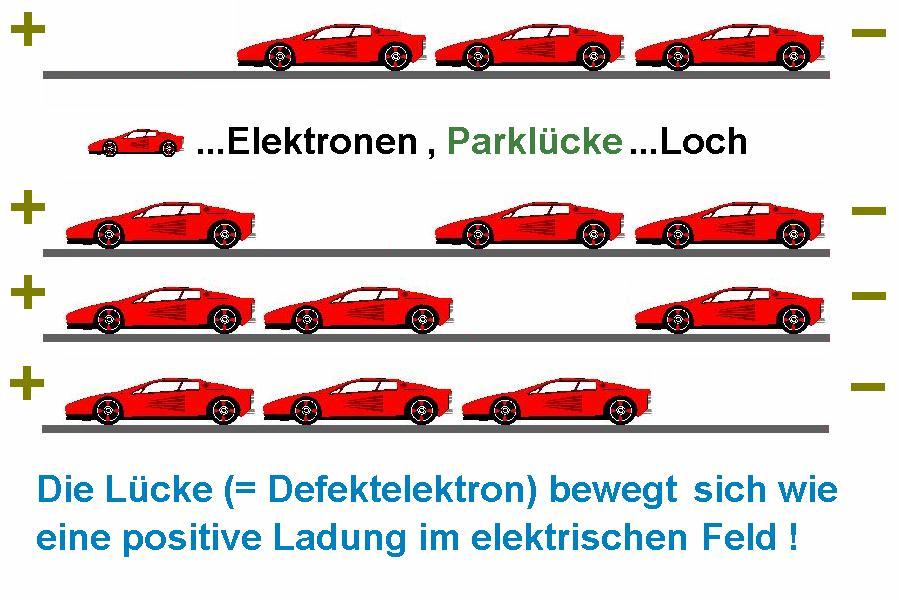
Betrachten wir nun die Verhältnisse bei Halbleiter genauer. Bei sehr tiefen Temperaturen T ist das VB vollständig gefüllt und das LB leer. Der Halbleiter leitet in diesem Zustand den elektrischen Strom nicht. Erhöht sich allerdings die Temperatur T, so gelangen immer mehr Elektronen aus dem VB ins LB, wo sie dann die elektrische Leitfähigkeit erhöhen. Die im VB zurückgebliebenen Leerstellen nennt man Defektelektronen oder Löcher. Auch diese tragen zur Leitfähigkeit bei, indem sie im elektrischen Feld wandern. Sie bewegen sich dabei in die Gegenrichtung der Elektronen, also quasi wie eine positive Ladung.
Mit zunehmender Temperatur gelangen also immer mehr Elektronen vom VB ins LB und erhöhen im Valenzband die Ladungsträgerkonzentration. Für diese gilt der Zusammenhang:

Zwischen dem elektrischen Widerstand R eines Körpers und seinen Abmessungen besteht folgender Zusammenhang:

Neben seinen geometrischen Abmessungen hängt sein Widerstand natürlich auch vom Material ab. Diese Materialabhängigkeit steckt im spezifischen Widerstand ρ. Je besser ein Körper den elektrischen Strom leitet, desto geringer ist sein spezifischer Widerstand ρ. Diese Größe hängt wiefolgt mit der spezifischen Leitfähigkeit κ zusammen:

Die spezifische Leitfähigkeit κ ist direkt proportional zur Ladungsträgerkonzentration n. Es folgt daraus:
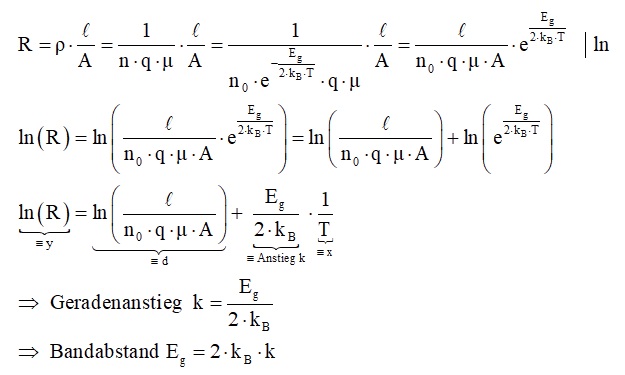
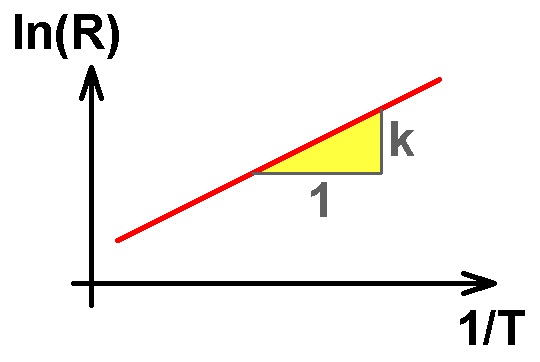
Trägt man also den ln(R) gegen 1/T auf, so müsste man eine steigende Gerade erhalten. Aus deren Anstieg k lässt sich dann der Bandabstand Eg ermitteln.
Experiment
Hier der gesamte Aufbau des Experiments:
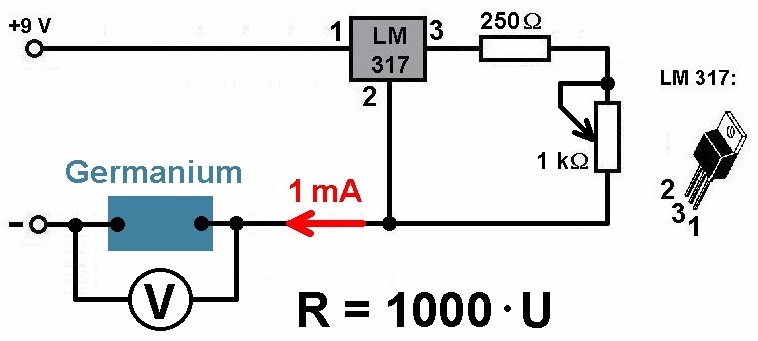
Mittels eines LM317 wird ein konstanter Strom von 1 mA durch den Halbleiter (Germaniumblock) geleitet. Durch die Verwendung des 1 kΩ Potentiometers bin ich die Stromstärke betreffend ein wenig flexibel. Um den Widerstand R des Halbleiters zu bestimmen, wird der Spannungsabfall U an ihm mit einem Voltmeter gemessen. Bei einer eingestellten Stromstärke von 1 mA ergibt sich der Widerstand R dann ganz einfach zu R = U/I = U/1 mA = 1000·U.
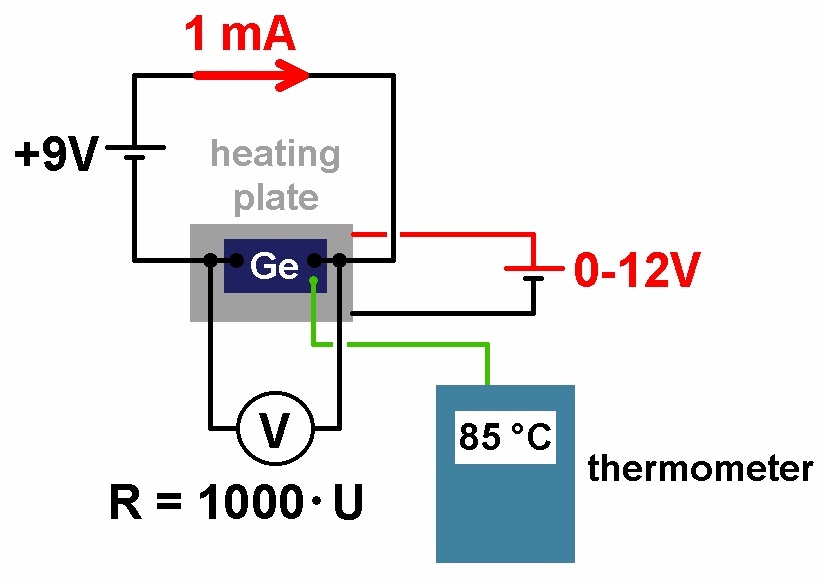
Diesen bestimmt man für verschiedene Temperaturen T im Bereich von 20°C und 160°C. Hierfür befindet sich der Germaniumblock auf einer regelbaren Heizplatte. Die Temperatur wird mit einem am Germanium befestigten Thermoelement bestimmt.


Der Wärmeleitkleber zur Fixierung des Germaniumblocks auf der Heizplatte und des Thermoelements am Germanium:
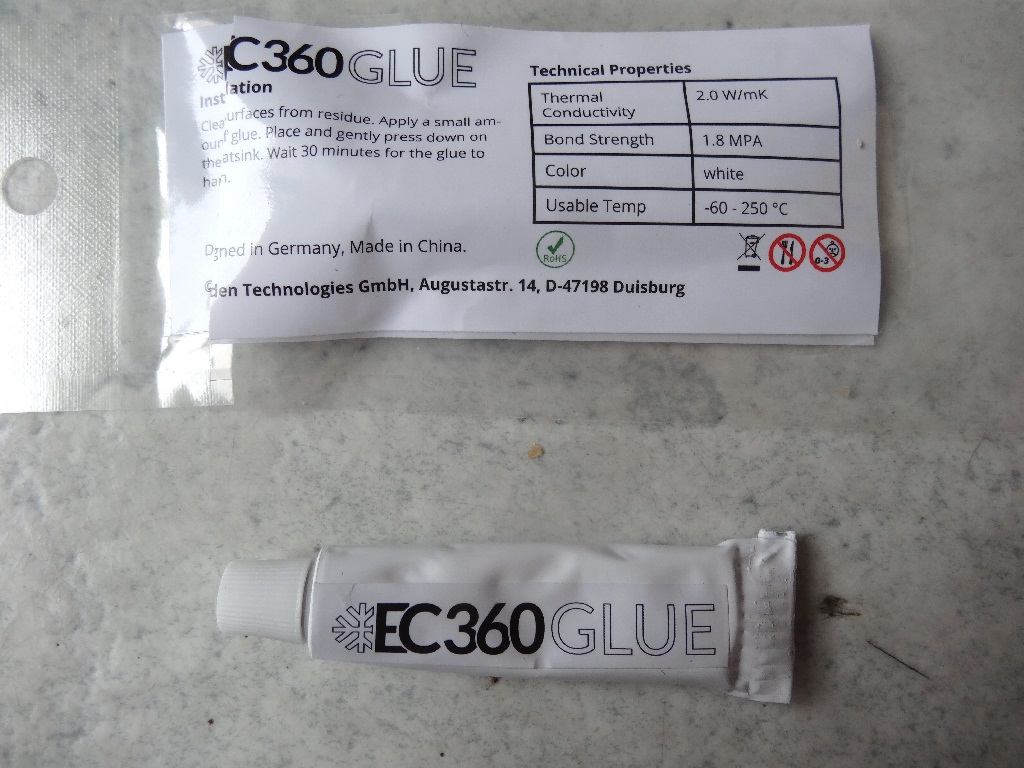
Da sich die Kabel aufgrund des Flussmittels im Lötzinn schlecht auf dem Germanium verlöten lassen, habe ich auf Amazon Fittingslot ohne Flussmittel bestellt. Damit ging es dann einigermaßen…

Die Konstantstromquelle mit dem LM317 habe ich einmal gelötet und sie funktioniert wie sie soll.

Das Germanium ist heute mit der Post angekommen:


Wie schon erwähnt war das Verlöten der Kabel auf dem Germanium nicht ganz einfach. Daher sehen die Lötstellen auch nicht gerade vorbildlich aus. Schönheitswettbewerb gewinne ich mit ihnen mit Sicherheit nicht 😉

Der komplette Aufbau ist mittlerweile fertig und ich konnte eine Messreihe aufnehmen.





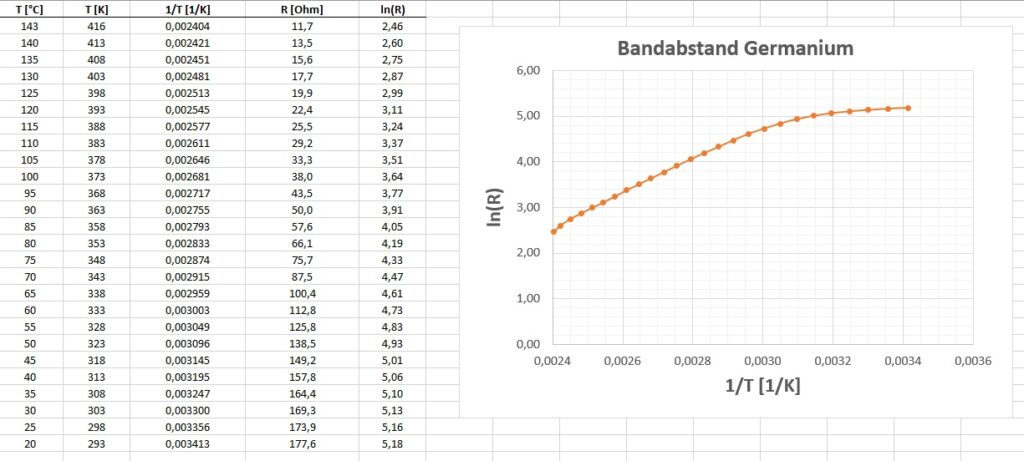
Bei einer Temperatur von 113.3 °C beträgt der Widerstand des Germaniums nur noch 27 Ω. Bei Raumtemperatur betrug dieser immerhin 178 Ω.


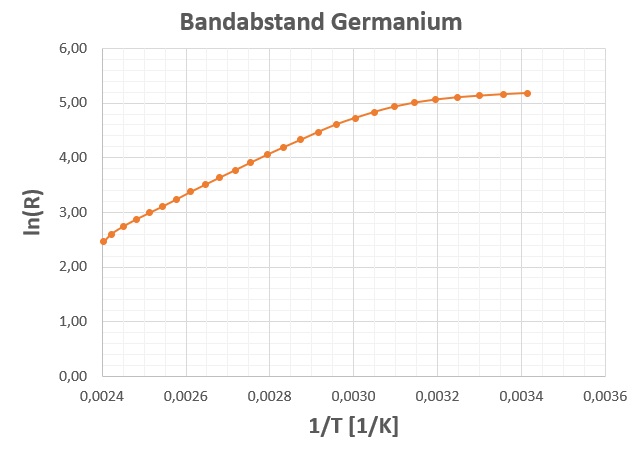
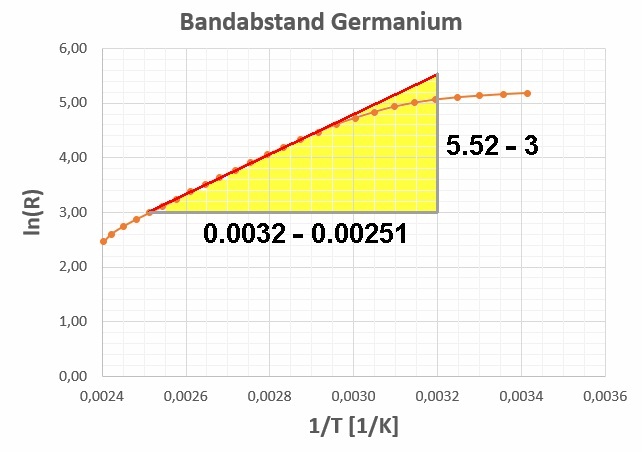
Trägt man die inverse absolute Temperatur 1/T gegen den ln(R) auf, so müsste sich der Theorie nach eine ansteigende Gerade ergeben. Dies konnte experimentell zumindest teilweise (siehe Graph unten) bestätigt werden. Aus dem Anstieg k und der Boltzmannkonstante ermittelte ich einen Bandabstand von Germanium von 0.63 eV. Dieser Wert stimmt sehr gut mit dem Sollwert überein 🙂
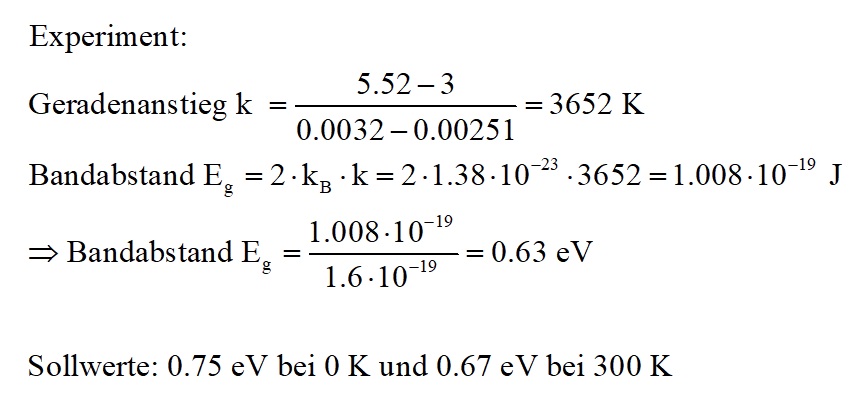
Zum Abschluss noch das Youtube-Video:

