
Bildquellen: Wikipedia
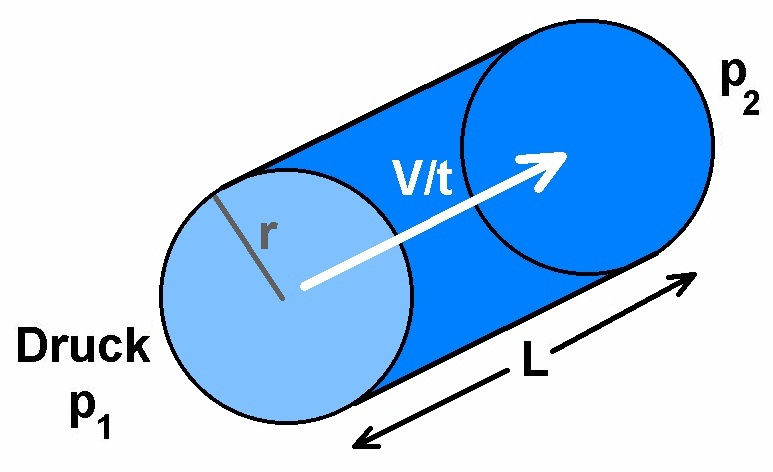
Das Hagen Poiseuille Gesetz, benannt nach den beiden Personen Gotthilf Hagen und Jean Poiseuille, beschreibt den Volumsstrom V/t einer laminaren Strömung durch ein Rohr mit dem Radius r. Auffallend ist die starke Abhängigkeit von V/t von r, nämlich in Form von r ^4. Ein doppelt so dickes Rohr lässt also bei gleichem Druckunterschied innerhalb einer bestimmten Zeit die 16-fache Menge an Flüssigkeit durchfließen.

Hier die doch sehr kurze (einfachere) Herleitung des Hagen-Poiseuille-Gesetzes:

Mit diesem Geschwindigkeitsprofil v(r) lässt sich dann der Volumsfluss V/t durch Integration über dr berechnen:

Der dazugehörige Versuch ist sehr einfach. Zwei unterschiedlich dicke aber gleich lange Schläuche sind über ein Absperrventil mit einem Wasserreservoire verbunden. Man öffnet das Ventil und lässt eine bestimmte Zeit t das Wasser durch beide Schläuche in jeweils einen eigenen Auffangbehälter fließen. Danach bestimmt man die beiden Volumina V1 und V2 und setzt sie in Relation zueinander. Es muss dann gelten: V1/V2 = (r1/r2) ^ 4. 
Die beiden Schläuche und die Schlauchverbinder habe ich über Amazon bestellt bzw. beim örtlichen Baumarkt besorgt, den Rest der Teile hatte ich bereits zuhause. Ich habe mich für Schläuche mit dem Innendurchmesser 2 mm bzw. 3 mm entschieden. Demnach sollte das Verhältnis der beiden Wasservolumina konkret 1.5 ^ 4 ≈ 5 betragen.






Nachdem ich sämtliche Teile beisammen hatte, konnte ich mit dem Versuch starten. Wie immer muss meine Küche oder das Wohnzimmer dafür herhalten 😉


Die beiden unterschiedlich dicken Schläuche müssen für den Versuch natürlich die gleiche Länge haben, denn es geht ja der Druckunterschied Δp pro Meter in die Formel ein und dieser muss bei beiden Schläuchen gleich sein.



Es ist gar nicht so einfach einen konstanten Volumsfluss durch beide Schläuche zu erzielen. Manchmal muss man einen der beiden zuhalten oder an einem kurz saugen. Ich konnte aber einige erfolgreiche Versuche durchführen. Während sich beim dicken Schlauch (3 mm) innerhalb der Messdauer rund 55 ml gesammelt haben, waren es beim dünnen Schlauch (2 mm) nur 12 ml. Das experimentelle Verhältnis der Volumsflüsse beträgt also 55/12 = 4.58. Damit liege ich gar nicht so weit vom theoretischen Wert 5.06 entfernt, Heureka…




Das Youtube-Video reiche ich wie immer nach…

