Gleich vorweg: Inspiriert wurde ich zu diesem Versuch von einer schon recht alten (1997), aber für mich immer noch äußerst wertvollen CD mit über 400 Freihandversuchen aus vielen Bereichen der Physik von der Universität Augsburg/Deutschland.

Literatur: Hilscher, H.: Universität Augsburg, Institut für Didaktik der Physik, CD-ROM Freihandexperimente

Bezugsquelle: https://www.isbn.de/buch/9783933446015/physikalische-freihandexperimente

Glas ist ja für sichtbares Licht und darüber hinaus sehr transparent. In diesem Versuch möchte ich aber zeigen, dass Glas hindurchtretendes Licht dennoch stark abschwächen kann und zwar durch Reflexionen an den Grenzschichten. Die Fresnelgleichungen waren bereits Thema eines meiner Physikprojekte (https://stoppi-homemade-physics.de/fresnel-gleichungen/). Sie beschreiben den Reflexionsgrad für unterschiedlich polarisiertes Licht in Abhängigkeit vom Einfallswinkel α.

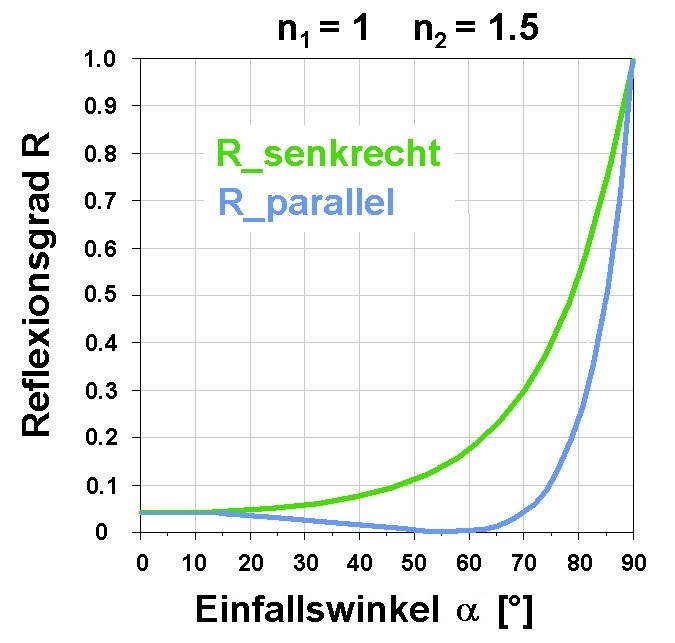
Wie man anhand des Graphen erkennen kann, liegt der Reflexionsgrad für den Übergang Luft-Glas bei senkrechtem Einfall (Einfallswinkel α = 0°) bei rund 0.04, also nur 4%. Genau für diesen Fall des senkrechten Einfalls vereinfachen sich die Fresnelgleichungen zu folgender einfachen Beziehung:

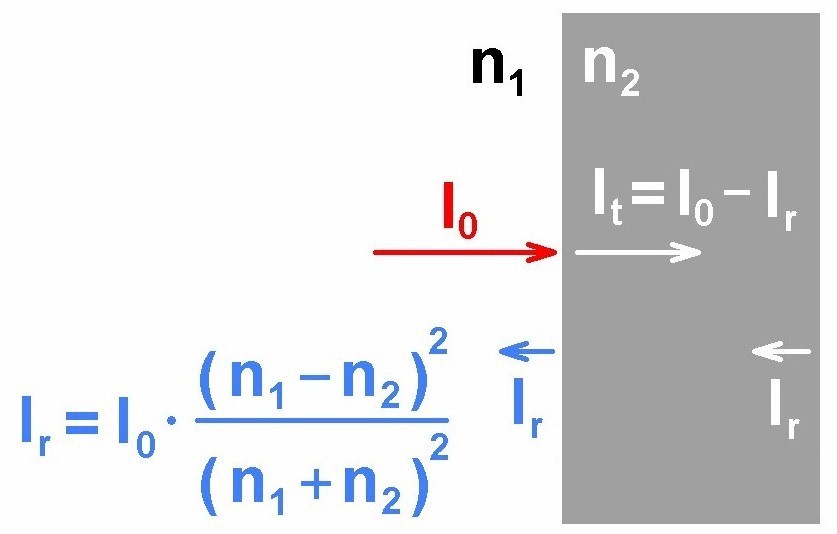
Setzt man in diese Formel n₁ = 1 für Luft und n₂ = 1.5 für Glas ein, erhält man: I_r = I₀ · (1.5 – 1)² / (1.5 + 1)² = I₀ · 0.04, also genau den oben erwähnten Reflexionsgrad von 4% beim Übergang Luft-Glas bzw. Glas-Luft.

Lässt man nun einen Laserstrahl durch viele einzelne Glasplatten strahlen, so kommt es an jedem einzelnen Übergang zu einer Reflexion von 4%, d.h. nur noch 96% der Intensität dringen weiter vor. Bei vielen Glasplatten führt dies dazu, dass der Laserstrahl doch massiv abgeschwächt wird, trotz der ausgezeichneten Transparenz von Glas.

Die Herleitung einer Formel für die hindurchtretende Lichtintensität I(x) in Abhängigkeit von der Anzahl x der Glasplatten ist sehr einfach:

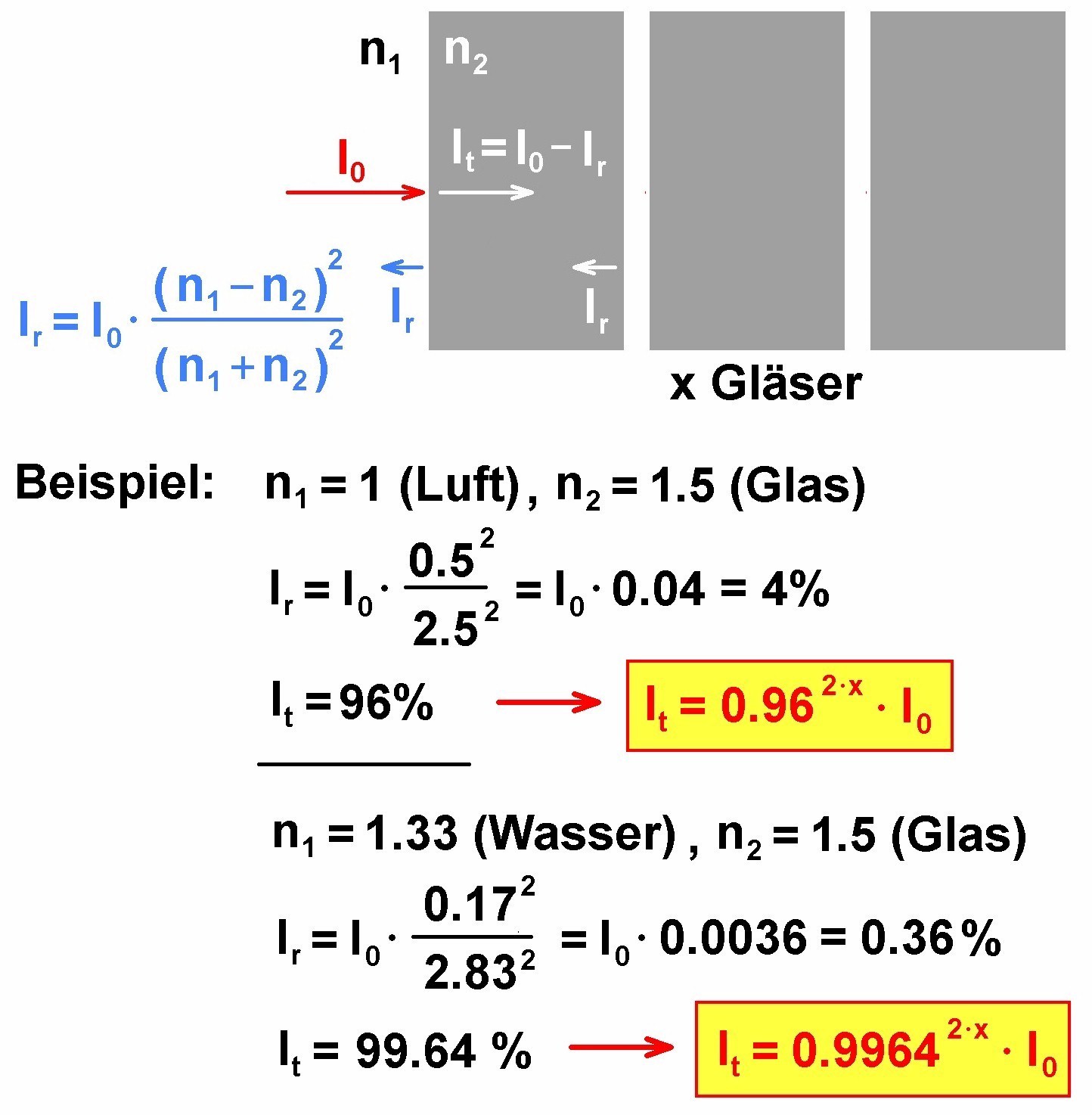
Jede einzelne Glasplatte schwächt das Laserlicht durch Reflexion zweimal, beim Eintritt und beim Austritt. Das bedeutet, dass jede einzelne Glasplatte die einfallende Intensität um den Faktor 0.96 · 0.96 = 0.96² abschwächt. Bei zwei Glasplatten beträgt die gesamte Abschwächung (Anm.: die Lichtaborption innerhalb des Glases wird hier vernachlässigt!) 0.96² · 0.96² = 0.96 ^ (2 + 2), bei drei Platten 0.96^ (2 + 2 + 2), allgemein bei x Platten demnach 0.96^ (2 · x). Bei zum Beispiel x = 30 Glasplatten sollte die Transmission nur noch ca. 10% betragen. Glas kann also scheinbar doch undurchsichtig werden…

Befindet sich zwischen den Glasplatten nicht Luft (Brechungsindex n ≈ 1) sondern Wasser (n = 1.33), so verringert sich der Reflexionsgrad von 4% auf nur noch 0.36% an jeder Grenzschicht. Die Folge ist, dass der Laserstrahl deutlich weniger abgeschwächt wird. Genau dies möchte ich experimentell überprüfen.

Für das Experiment werden nur ein Laser, Mikroskop-Objektträger aus Glas, Wasser + Pipette und ein Lichtsensor benötigt.

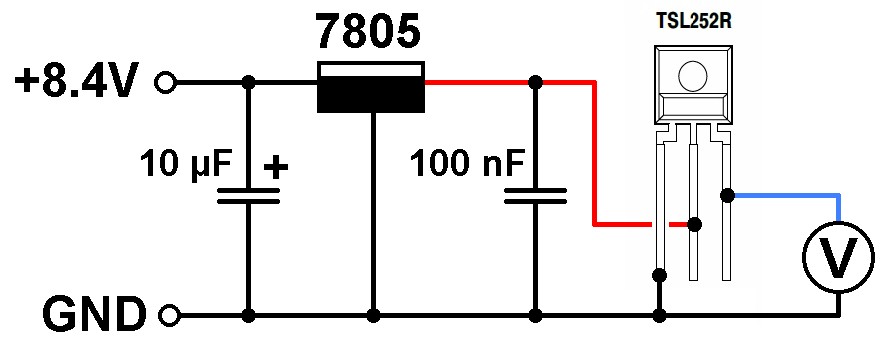
Für die Erfassung der durchscheinenden Laserintensiät verwende ich den Sensor TSL252R. Hier die einfache Schaltung:

Da der Sensor aber selbst bei einem leistungsschwachen Laser mit nur 5 mW total übersteuert, musste ich den Strahl mittels Neutraldichtefilter auf nur 1% abschwächen:

Im ersten Teil des Experiments postierte ich an Luft einen Objektträger nach dem anderen hintereinander und bestimmte jeweils die hindurchtretende Lichtintensität:

Die Ausgangsspannung am Lichtdetektor nahm dabei von U = 3.29 V ohne Glasplatten auf U = 0.83 V bei 12 Glasplatten ab:

Im zweiten Teil des Experiments gebe ich mit einer Pipette Wasser zwischen die einzelnen Glasplatten und stelle diese dann in eine mit Wasser gefüllte, flache Schale:

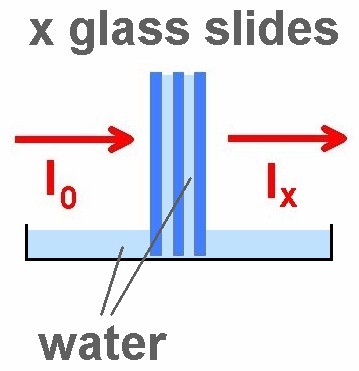
Bei 12 Glasträgern sank nun die Spannung am Lichtdetektor lediglich von 3.29 V auf 2.64 V. Zum Vergleich: Ohne Wasser betrug die Spannung bei 12 Gläsern nur noch 0.83 V!

Die beiden experimentell ermittelten Graphen U(x) ohne/mit Wasser sehen wiefolgt aus:

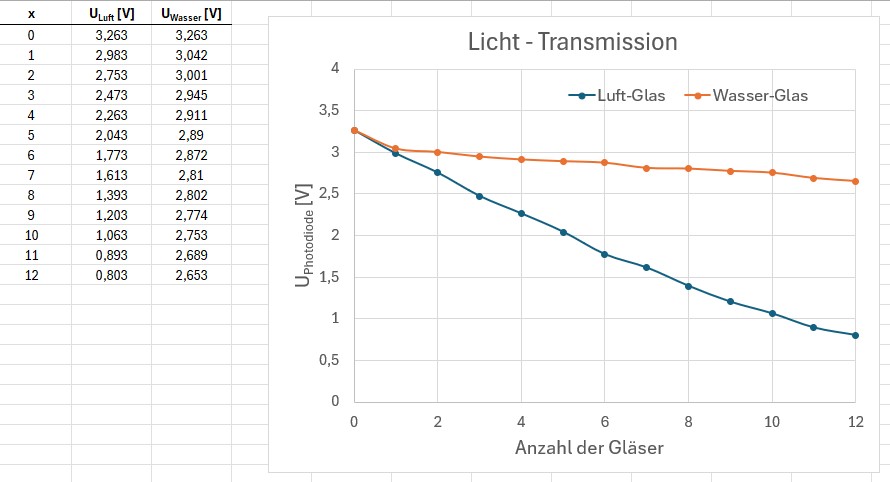
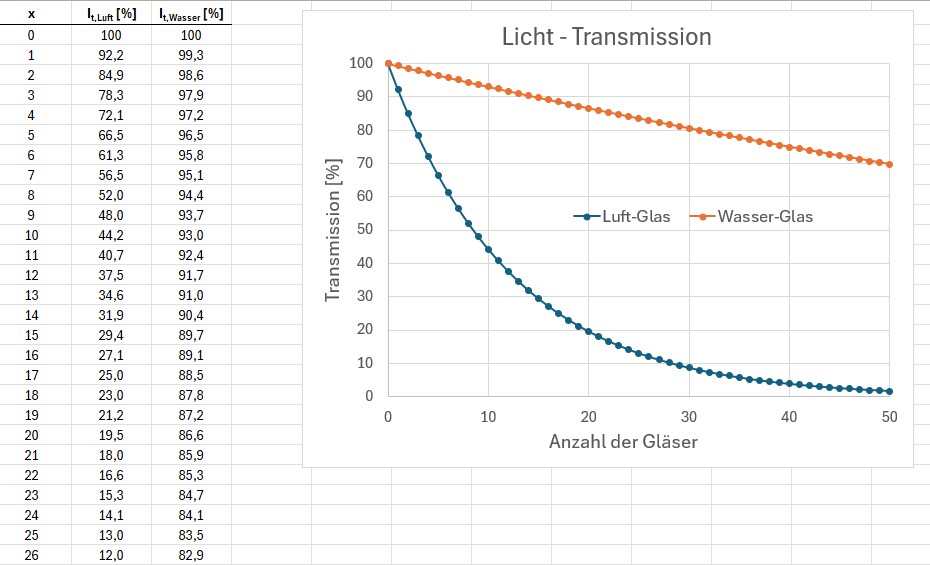
Kleine Anmerkung zum Graphen mit Wasser: Dieser verläuft deshalb für x = 0 und x = 1 gleich wie jener für Luft, da ja bei keinem bzw. nur einem Objektträger kein Wasser hinzugefügt werden kann! Erst ab x = 2 konnte ich Wasser zwischen die Gläser geben…

Man erkennt aber deutlich, dass die Transmission bei Verwendung von Wasser zwischen den Gläsern stark erhöht ist. Ohne Wasser sinkt die Spannung/Lichtintensität bei nur 12 Gläsern bereits auf rund 1/4, also 25 % ab. Glas kann also in der Tat durchaus undurchsichtig werden, Heureka 😉

Excel-Datei: Reflexion_undurchsichtiges_Glas_Excel

Das Youtube-Video reiche ich wie immer nach…