Bildquelle: Wikipedia
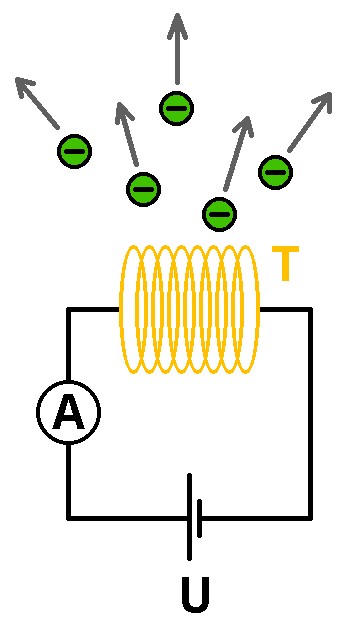
Ohne Richardson-Effekt gäbe es keine alten Röhrenfernseher oder Elektronenröhren. Bei diesem nach dem Physiker Owen Willans Richardson (1879 – 1959) benannten Effekt geht es um das Austreten von Elektronen aus einer mittels Strom geheizten Glühkathode.
Die Sättigungsstromdichte wurde 1901 von ihm rechnerisch in der Richardson-Gleichung erfasst, wofür er 1928 mit dem Nobelpreis für Physik ausgezeichnet wurde. Jene Sättigungsstromdichte J = Stromstärke / Fläche = I / A mit der Einheit Ampere pro Quadratmeter steigt logischerweise mit zunehmender Temperatur T der Glühwendel stark an. Die Formel lautet:
Damit Elektronen aber das Metall der Glühwendel verlassen können, muß dieses eine Temperatur von > 900 K aufweisen. Die Glühemission findet zumeist im Vakuum statt und wird/wurde wie schon erwähnt etwa bei Elektronenröhren ausgenützt. Genau eine solche alte Elektronenröhre bildet auch das Herzstück des Experiments.
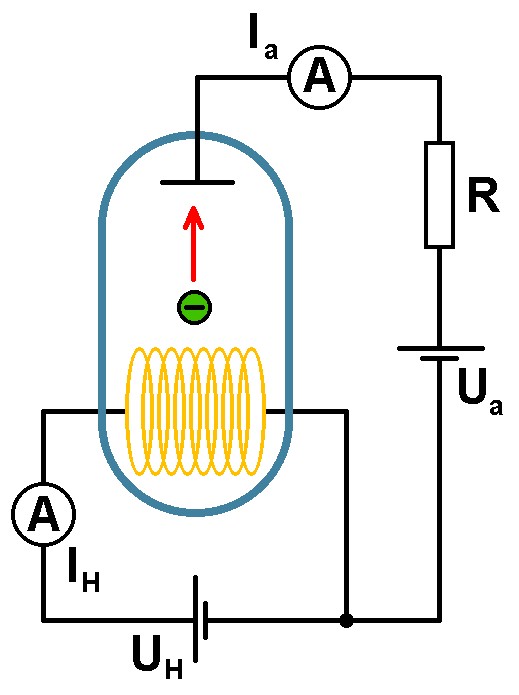
Mit der Heizspannung UH und dem daraus sich ergebenden Heizstrom IH wird die Glühwendel auf eine bestimmte Temperatur T gebracht. Die von der Glühwendel emittierten Elektronen werden durch die positiv gepolte Anode abgesaugt und ergeben den Anodenstrom Ia. Werden sämtliche Elektronen zur Anode geleitet gilt: Stromdichte J · Glühwendelfläche A (Achtung: Nicht zu verwechseln mit der Richardson-Konstante A) = Anodenstrom Ia. Der Anodenstrom ist also direkt proportional zur Stromdichte J.
Trage ich ln(Ia/T²) in Abhängigkeit von 1/T auf, so müsste ich eine fallende Gerade erhalten. Ihr Anstieg k beträgt –We/kB. Der Graph müsste im Idealfall so aussehen:
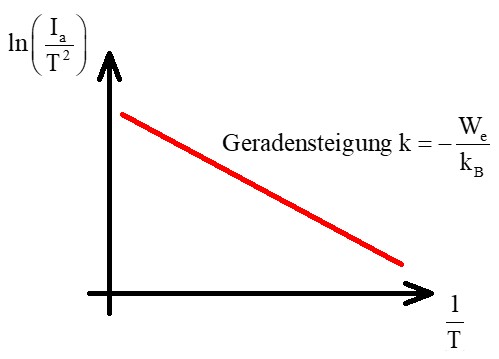
Mittels der experimentell ermittelten Geradensteigung kann man demnach die Auslösearbeit We für Elektronen aus dem Metall ermitteln. Für reines Wolfram sollte diese bei 4.5 – 4.6 eV liegen, für thoriertes Wolfram nur bei 2.6 – 2.7 eV. Diese Werte habe ich mittels ChatGPT erfragt:
Wie messe ich aber nun die Temperatur T der Glühwendel? Nun, je heißer die Glühwendel wird, desto größer ist ihr ohmscher Widerstand R. Aus dem aktuellen Widerstand R und jenem bei Raumtemperatur lässt dich die Temperatur bestimmen. Es gilt nämlich folgender Zusammenhang zwischen R(T) und der Temperatur T:
Es gibt Elektronenröhren mit direkt und indirekt geheizter Kathode. Bei der direkt geheizten ist der Glühfaden gleichzeitig auch Kathode. Bei der indirekt geheizten befindet sich die Kathode nur sehr nahe zur separaten Glühwendel. Im letzteren Fall besitzt wohl die Kathode nicht die ganz gleiche Temperatur wie die Glühwendel, sondern eine etwas geringere. Daher suchte ich für diesen Versuch eine Elektronenröhre mit direkter Heizung. Gefunden habe ich die Röhre AG1006:
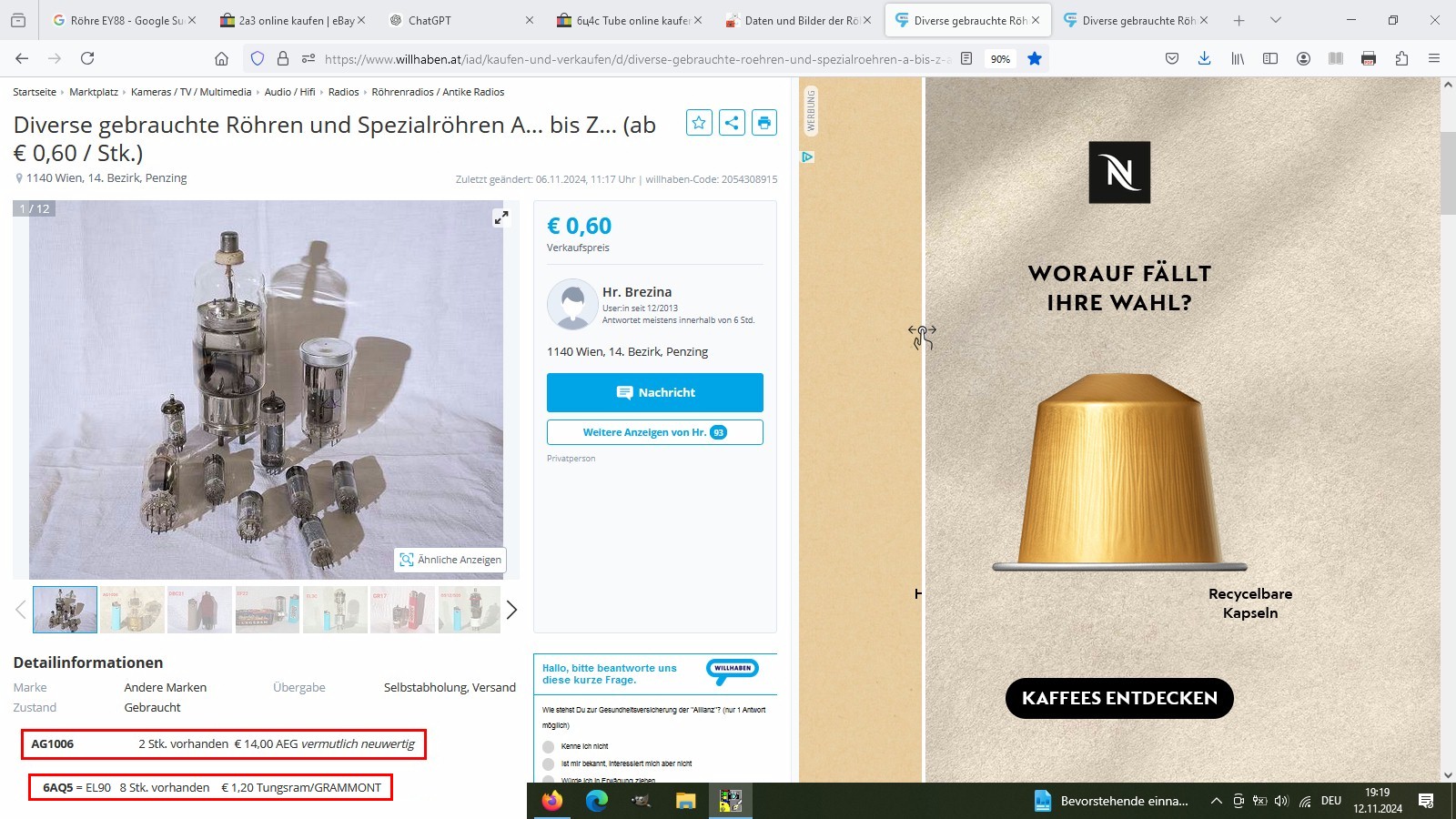
Ihre Heizspannung beträgt 3V und der Heizstrom 3 A.
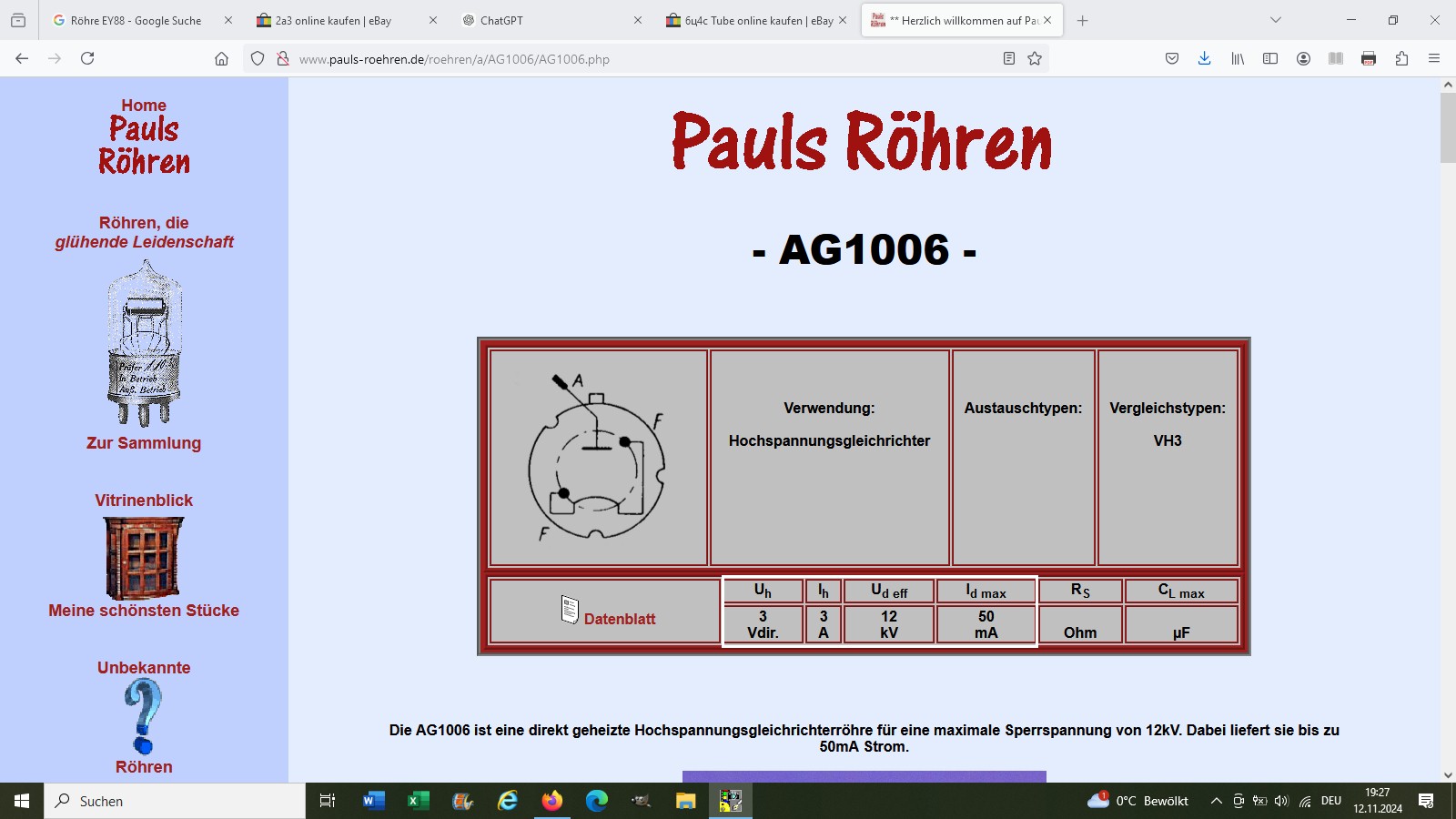
Quelle: http://www.pauls-roehren.de/roehren/a/AG1006/AG1006.php
Um herauszufinden, aus welchem Material deren Glühwendel ist, habe ich wieder ChatGPT bedient:
Die Röhre ist inzwischen gut bei mir angekommen:
Mit der Richardson-Gleichung lässt sich bei bekannter Fläche A der Glühwendel die Stromstärke durch Glühemission bestimmen. Angenommene Werte A = 100 mm², Kathodenmaterial Wolfram:
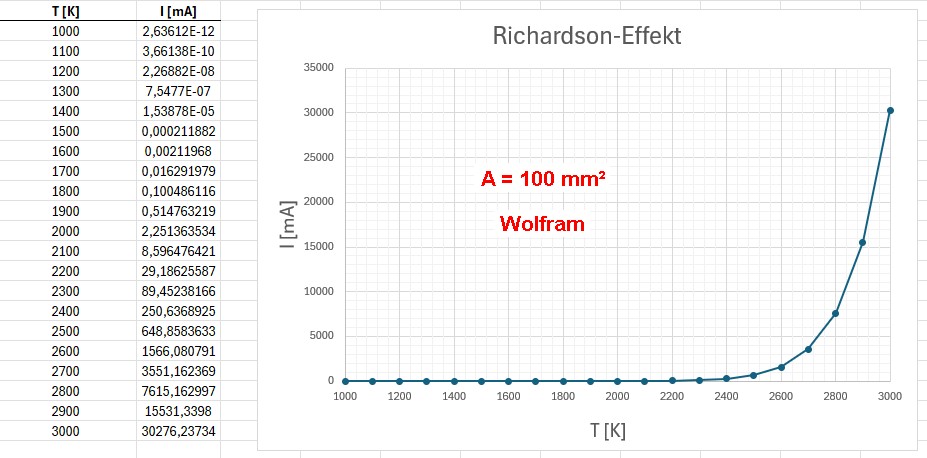
Bei einer Glühwendeltemperatur von 2800 K beträgt die Stromstärke schon beachtliche 7.6 Ampere (!). Von daher werde ich nicht so hoch mit der Temperatur raufgehen. Bei T = 1500 K sollte die Stromstärke 0.2 µA betragen, bei 1800 K bereits 100 µA und bei 2200 K dann 29 mA:
Das Experiment konnte ich in der Zwischenzeit durchführen. Zur Messung des Anodenstroms kommt mein Nanoamperemeter zum Einsatz:
Der gesamte Aufbau:
Die Anodenspannung betrug 20 V, der Anodenwiderstand zur Limitierung des Anodenstroms 390 Ohm:
Bei einer Heizspannung von 1.755 V…
und einem Heizstrom von 2.43 A…
betrug der Anodenstrom 1784 µA:
Zur Bestimmung der Temperatur T der Glühwendel benötigte ich deren Widerstand bei Raumtemperatur. Ich maß ihn mittels gewöhnlichen Spannungsteiler:
Die Messergebnisse:
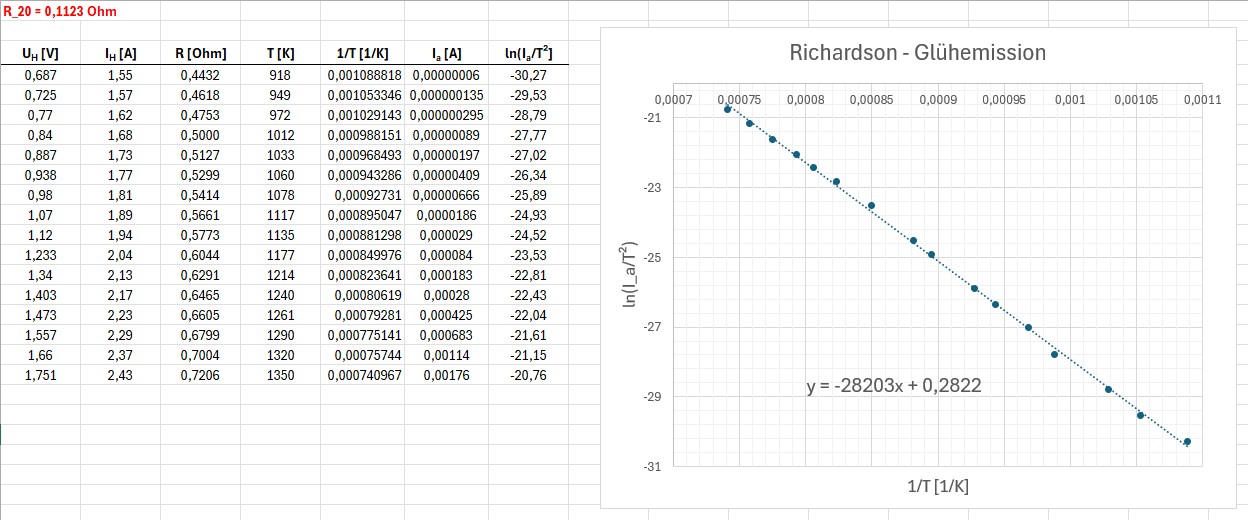
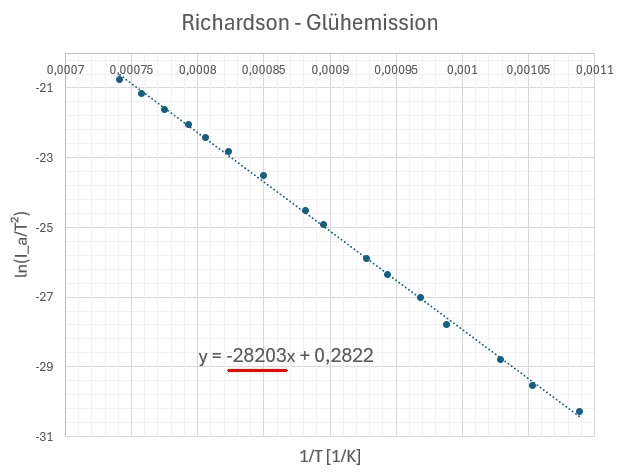
Die Geradensteigung beträgt also –28203 K. Damit konnte ich die Ablöseenergie We der Elektronen bestimmen:
Das Datenblatt zur AG1006 Röhre konnte ich dann auch noch im Internet finden. Dort ist angegeben, dass es sich um eine thorierte Wolframkathode handelt. Damit liegt mein experimentell erhaltener Wert von 2.43 eV für die Ablösearbeit gar nicht so weit vom Sollwert zwischen 2.6 und 2.7 eV entfernt, Heureka 😉
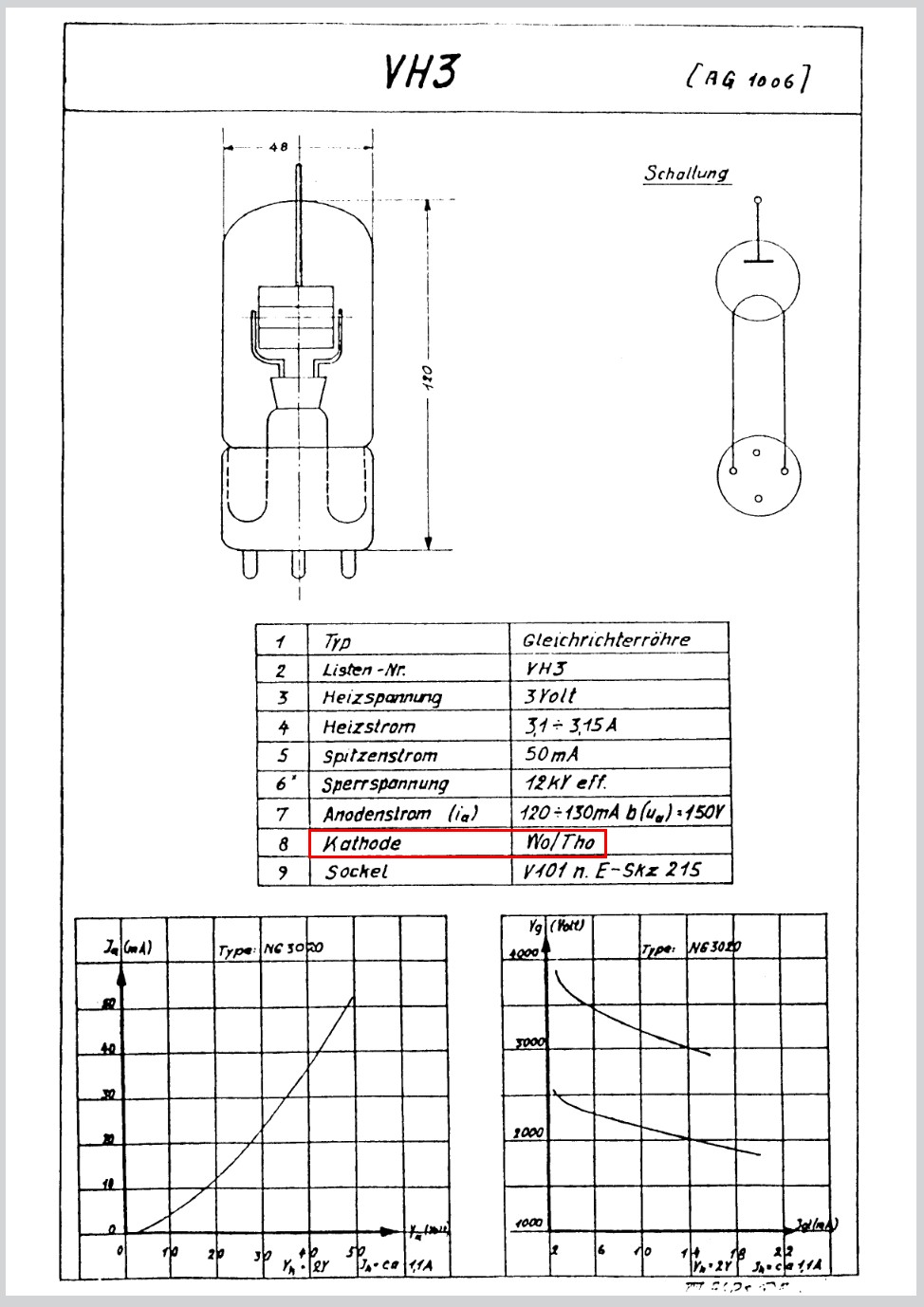
Quelle: http://www.pauls-roehren.de/roehren/a/AG1006/AG1006.php
Das Youtube-Video reiche ich wie immer nach…
