
Bildquelle: https://www.mpp.mpg.de/ueber-uns/geschichte
Der deutsche Physiker Werner Heisenberg (1901-1976) gilt als einer der bedeutendsten theoretischen Physiker. 1927 formulierte er die nach ihm benannten Unschärferelationen, für die er 1932 auch den Nobelpreis in Physik bekam. Sie treten in zwei Formen auf:
- Orts- und Impulsunschärfe: Δx · Δp > h/4π
- Energie- und Zeitunschärfe: ΔE · Δt > h/4π
Was sagen diese beiden Unschärferelationen aus? Nehmen wir einmal die Orts- und Impulsunschärfe. Sie besagt, dass die Unschärfen/Unsicherheiten bzgl. Ort und Impuls nicht zugleich (!) beliebig klein werden können. Das Produkt beider Unschärfen muss also zwingend größer als h/4π sein (h … Plancksche Wirkungsquantum mit h = 6.63 * 10^ –34 Js). Es gibt also unabhängig von der Art und Genauigkeit der Messung eine gewisse Unschärfe/Unsicherheit, die nicht umgangen werden kann.
Im Alltag spielen diese Unsicherheiten/Unschärfen durch den extrem kleinen Wert von h natürlich keine Rolle. Die auf den Messungen beruhenden Ungenauigkeiten sind viel, viel größer. Zweifelsohne kann man schon etwa stolz sein, den Ort eines Autos auf µm genau zu kennen. Wo aber spielen dann diese von der Natur selbst vorgegebenen Unschärfen eine Rolle? Im atomaren Bereich…
Die Ort- und Impulsunschärferelation sagt aus, dass eine geringere Ortsunschärfe Δx eine größere Impulsunschärfe Δp bedingt und umgekehrt. Beides kann nicht beliebig genau angegeben werden. Dies hat aber zum Beispiel weitreichende Folgen für die Stabilität der Atome.
Man wusste damals bereits, dass beschleunigte elektrische Ladungen elektromagnetische Wellen absenden und dadurch Energie verlieren. Ein um den Kern kreisendes Elektron vollführt aber genau so eine beschleunigte Bewegung (Anm.: Die Beschleunigung auf einer Kreisbahn beträgt a = v²/r = Zentripetalbeschleunigung). Demnach müsste das Elektron eigentlich Energie abstrahlen und dadurch in den Kern „fallen“. Dies ist aber nicht der Fall. Warum aber? Zuerst postulierten Physiker wie Niels Bohr einfach stabile Bahnen für das Elektron, konnten dies aber nicht erklären.
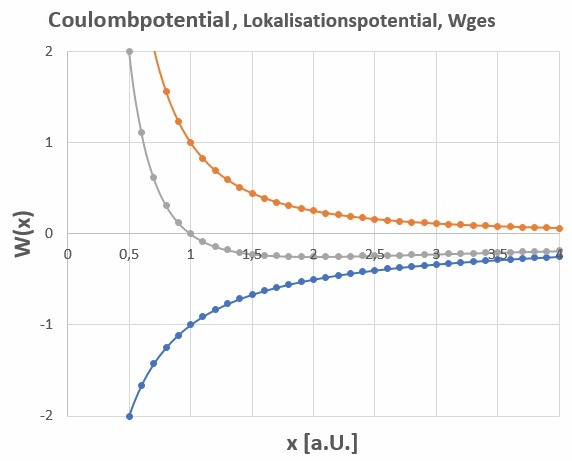
Mit der Heisenbergschen Unschärferelation wurde dies aber klarer. Angenommen ein Elektron würde sich dem Kern nähern. Demzufolge wäre sein Ort genauer lokalisiert und die Ortsunschärfe Δx dadurch geringer. Laut Unschärferelation müsste dann im Gegenzu seine Impulsunschärfe Δp wachsen. Für die kinetische Energie des Elektrons gilt aber Ekin = p² / 2m. Demnach würde auch die kinetische Energie wachsen und das Elektron könnte somit einen Sturz in den Kern verhindern. Neben der potentiellen Energie auf Basis der Coulombanziehung (Wpot = –1/r) tritt also auch eine sog. Lokalisationsenergie auf Basis der Heisenbergschen Unschärferelation auf (Wkin = p²/2m > Δp²/2m > h²/(32·m·π²·Δx²)) auf, welche also eine 1/r²-Abhängigkeit zeigt.
Diese kinetische Energie kommt nicht durch irgendeine Bewegung zustande, sondern einzig und allein durch die Einschränkung des Aufenthaltsbereiches!
Coulombpotential und Lokalisationsenergie überlagern sich zur Gesamtenergie. Diese besitzt ein Minimum bei einem bestimmten Radius r, da für sehr kleine Radien die 1/r² Abhängigkeit der Lokalisationsenergie gegenüber der –1/r Abhängigkeit des Coulombpotentials dominiert!
Die beiden Heisenbergschen Unschärferelationen lassen sich aber auch experimentell mit einfachen Mitteln untermauern.
Experiment zur Orts-Impuls-Unschärfe
Varinte 1:
Für diesen Versuch benötigen wir nur einen Laserpointer und einen sehr schmalen Spalt. Leuchten wir mit dem Laser auf den Spalt, so erkennen wir dahinter keinen kleinen Punkt, sondern ein sog. Beugungsmuster mit Maxima und Minima. Wir beobachten weiters, dass bei einer Verringerung der Spaltbreite die Beugungsmuster breiter werden. Kleinerer Spalt bedingt stärkere Beugung. Nun die Spaltbreite können wir als Ortsunschärfe Δx der Photonen betrachten und die Beugung zu den Seiten hin als Impulsunschärfe Δp. Je kleiner nun Δx wird, umso stärker wird die Beugung, sprich umso größer wird Δp. Wir können mittels der Formel für die Beugung am Spalt und der de Broglie Beziehung sogar eine Art/die Unschärferelation wie folgt herleiten:




Wir können auch konkret überprüfen, ob für den Fall der Beugung am Spalt die Heisenbergsche Unschärferelation erfüllt ist. Hierfür benötigen wir neben den Maßen des Beugungsbildes noch die de Broglie Beziehung λ = h/p, um bei gegebener Wellenlänge des Laser (λ = 532 nm) den Impuls p der Photonen zu berechnen. Es gilt:

Variante 2:
Für die zweite Variante benötigen wir ein Oszilloskop mit FFT (Fast Fourier Transformation), welche ein Signal in seine Frequenzanteile zerlegt. Ein reiner Sinus besitzt im Fourierspektrum nur eine Linie/Peak bei der Frequenz des Sinussignals. Eine Rechtecksschwingung besteht zum Beispiel schon aus mehreren Sinussignalen. Daher besitzt das Fourierspektrum eines Rechtecksignals mehrere „Linien“. Was hat dies aber alles mit der Heisenbergschen Unschärferelation zu tun?
Betrachten wir einen schönen Sinus. Wenn man diesen als Wellenfunktion betrachtet, so ist der Ort maximal undefiniert, d.h. die Ortsunschärfe Δx sehr groß. Die Aufenthaltswahrscheinlichkeit berechnet sich ja zu ψ·ψ∗, und wenn die Wellenfunktion (in unserem Fall der Sinus) nirgends verschwindet, ist auch die Aufenthaltswahrscheinlichkeit nirgends 0.

Das Frequenzspektrum eines einzelnen Sinussignals ist aber wie schon erwähnt eine einzige Linie eben bei der Frequenz des Sinus. Das bedeutet, dass die Frequenzunschärfe Δf sehr gering ist und demnach auch die Wellenlängeunschärfe Δλ. Nach der berühmten Beziehung von de Broglie p = h / λ ist aber in weiterer Folge auch die Impulsunschärfe Δp minimal, q.e.d.
Betrachten wir nun aber ein sehr kurzes Sinussignal, d.h. die Ortsunschärfe Δx soll dieses Mal sehr klein sein. Dieses kurze Sinuspaket besteht aber aus sehr vielen Sinussignalen, wenn man es sich zusammengesetzt vorstellt. Das Fourierspektrum besitzt also viele „Linien“. Jede einzelne Sinusschwingung besitzt aber nun eine eigene Wellenlänge und demnach auch einen eigenen, unterschiedlichen Impuls. Die Impulsunschärfe Δp ist daher sehr groß…
Für das Experiment benötigt man neben einem Digitaloszilloskop noch einen sehr günstigen Frequenzgenerator und eine kleine elektronische Schaltung bestehend aus einem NE555-Timer und einem CD4066 Transmissionsgatter.

Mit dem NE555 zerhackt man das Sinussignal des Funktionsgenerators in kürzere Pakete. Den Durchlass (quasi ein Schalter) regelt der CD4066.
Zuerst stellt man mit den beiden Potentiometern bei der Timerschaltung einen quasi kontinuierlichen Sinus ein. Wenn ein Hund (und nicht Schrödingers Katze) anwesend ist, kann man diesen ja wie in meinem Fall um Hilfe bitten 😉



Das Fourierspektrum besteht nun wie oben erläutert aus einem einzelnen, schmalen Peak genau bei der Frequenz des Sinussignals:

Nun regelt man den Timer so, dass die Sinuspakete immer kürzer werden:

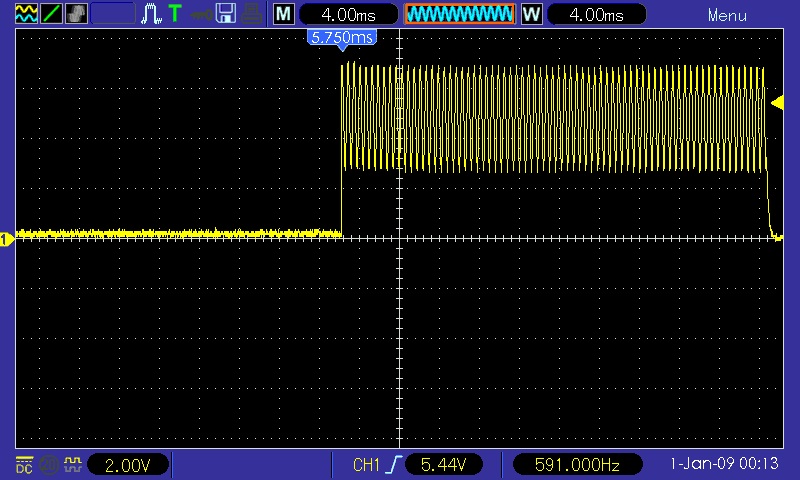
Der Peak im Fourierspektrum wird zunehmend breiter, wie man hier schön sieht:

Ist das Sinuspaket nur noch ganz kurz (geringe Ortsunschärfe Δx), so ist das dazugehörige Frequenzspektrum sehr breit (große Impulsunschärfe Δp):


Zum Schluss mein Youtube-Video…
… und ein Link: https://www.experimente.physik.uni-freiburg.de/H_Atom_und_Kernphysik/versuchemitelektronenundmateriestrahlen/heisenbergakustikanalogie
Experiment zur Energie-Zeit-Unschärfe
Die Energie-Zeit-Unschärferelation besagt, dass Energie- und Zeitunschärfen nicht zugleich beliebig klein werden können. Wählt man eine sehr, sehr kleine Zeitspanne Δt, so kann/muss die Energieunschärfe ΔE sehr groß werden. Dies hat aber zur Folge, dass etwa auch im Vakuum für sehr kurze Zeit große Energien bereitgestellt werden können, die dann zum Beispiel zur Schaffung von Teilchen/Antiteilchen genutzt werden. Dies nennt man dann Vakuumfluktuationen. Auf diese Weise soll ja auch im Rahmen des Urknalls Materie geschaffen worden sein.
Man kann die Energie-Zeit-Unschärfe aber auch wiefolgt auslegen: Die Zeitunschärfe ist die Verweildauer der Elektronen im angeregten Zustand und die Energieunschärfe ist dann die Unschärfe der Energie dieses Zustands. Verweilt also ein Elektron sehr lange im angeregten Zustand (Δt groß), so wird die Energieunschärfe des Zustands sehr klein (ΔE klein). Eine geringere Energieunschärfe bedingt aber auch eine geringere Frequenzunschärfe des beim „Sprung nach unten“ emittierten Photons, da ja die Beziehung E = h · f gilt. Ist also die Energiesprosse im Termschema schärfer, so ist die beim „Sprung nach unten“ freiwerdende Energie schärfer und demnach auch die Frequenz des emittierten Photons. Normalerweise verweilen Elektronen im angeregten Zustand nur extrem kurze Zeit (ns-Bereich). Diese Zeiten sind für einen Hobbyphysiker (fast) nicht überprüfbar. In manchen Materialien wie etwa in einem Rubinstab verweilen die Elektronen aber verhältnismäßig lange im angeregten Zustand (im ms-Bereich). Diese Zeiten sind durchaus messbar. Den Rubinlaserstab konnte ich für ca. 45 Euro auf ebay.com aus Russland erwerben.
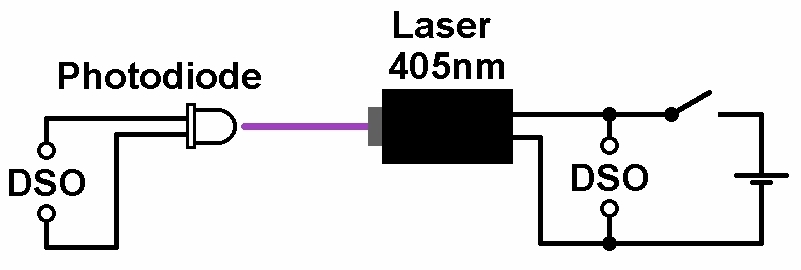
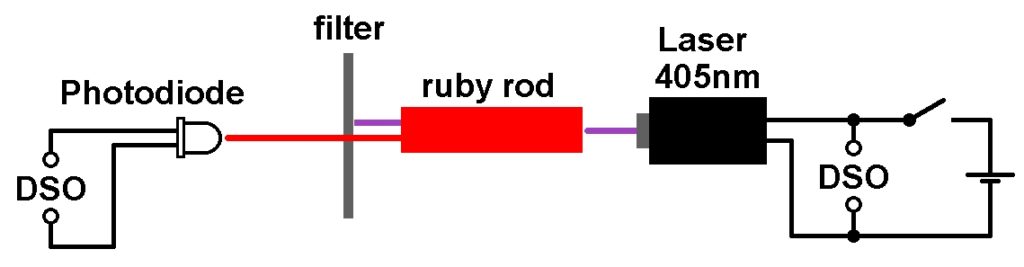
Wie misst man nun diese Verweilzeit? Man regt den Rubinlaser zunächst mit höherfrequentem Licht aus einem Bluray-Laser (λ = 405 nm) an. Dadurch befinden sich permanent viele Elektronen in einem angeregten Zustand. Schaltet man nun den Laser abrupt aus, so stoppt die „Nachlieferung“ und die verbleibenden, angeregten Elektronen kehren wieder in ihren Grundzustand zurück. Dabei emittieren sie aber noch Licht. Dieses Licht kann mit einem Lichtdetektor noch gemessen werden. Dabei ist eine exponentielle Abnahme der Intensität zu erwarten, da das angeregte Energieniveau durch die Sprünge der Elektronen nach unten immer leerer wird.
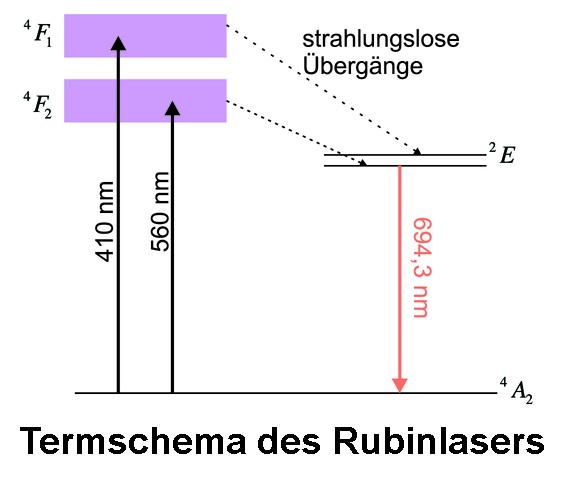
Während also das Anregungslicht (λ = 405 nm) durch Betätigung des Laserschalters abrupt endet, nimmt das Fluoreszenzlicht (λ = 694 nm) exponentiell ab. Anhand der Abnahme kann eine mittlere Lebensdauer Δt bestimmt werden. Hierfür ist der Spannungsausgang des Lichtdetektors mit einem Oszilloskop verbunden.
Konkret ergibt sich aus der exponentiellen Abnahme der Lichtintensität eine mittlere Lebensdauer von Δt = ca. 4 ms. Dies ist wie schon gesagt für atomare Zustände extrem lange.











Man erkennt schön die exponentielle Abnahme des vom Rubinstab emittierten Fluoreszenzlichts. Zum Glück hatte ich bei diesem Versuch professionelle Hilfe von meinem Sohn…

Ein großes Δt hat aber laut Heisenbergscher Unschärferelation eine sehr geringe Energieunschärfe ΔE zufolge. Das rote Fluoreszenzlicht des Rubinlaserstabs muss also eine sehr geringe Frequenz- bzw. Wellenlängenunschärfe besitzen. Dies kann man mit einem Spektroskop überprüfen. Mit einem Spektroskop lassen sich die von einer Lichtquelle emittierten Frequenzen bzw. Wellenlängen bestimmen. Postiert man also den Rubinlaserstab vor dem Eingangsspalt des Spektroskops, so lässt sich dessen Lichtspektrum untersuchen. Und in der Tat, das rote Licht des Rubinlasers besitzt eine sehr geringe Wellenlängenunschärfe oder anders ausgedrückt, dessen Spektrallinie ist sehr scharf.




