Die meisten werden die berühmte Einstein’sche Beziehung E = m·c² zwischen Energie und Masse kennen. Wo sie konkret auftritt, wissen schon weniger. Als wichtiges Beispiel ist die sog. Bindungsenergie von Atomen zu nennen, auf der exotherme Vorgänge wie die Kernfusion oder Kernspaltung beruhen.
Was versteht man unter der Bindungsenergie? Nehmen wir einmal Helium-4 her, welches aus 2 Protonen und 2 Neutronen besteht. Die Massen ungebundener/freier Neutronen und Protonen bzw. von Helium-4 betragen
mProton = 1.6726 · 10–27 kg, mNeutron = 1.6749 · 10–27 kg, mHelium-4 = 6.645 · 10–27 kg, 2 · mProton + 2 · mNeutron= 6.695 · 10–27 kg
Wie man sieht, ist die Masse von Helium-4 geringer als die Summe der Einzelmassen. Genau diese Massenabnahme (sog. Massendefekt) Δm geht nun in die berühmte Einstein-Beziehung E = m·c2 ein und entspricht der Bindungsenergie von Helium-4.
Konkret gilt für Helium-4:
EBindung = ∆m · c2 = 0.05 · 10–27 · (3 · 108)2 = 4.5 · 10–12 J = 28 MeV
EBindung/Nukleon = 28 MeV/4 = 7 MeV/Nukleon
Berechnet man nun die Bindungsenergie pro Nukleon für sämtliche Atome, so stellt man fest, dass dieser Wert nicht für alle Atome gleich ist. Er wächst zunächst mit zunehmender Massenzahl bis Nickel-62 an, um dann wieder abzunehmen. Welche weitreichende Konsequenzen hat dies aber nun?

Wäre die Bindungsenergie pro Nukleon für alle Atome gleich, würde man bei der Fusion (Verschmelzung) bzw. Fission (Spaltung) von Atomen keine Energie gewinnen. Es wäre ein Nullsummenspiel. Durch den besonderen Verlauf der Bindungsenergie/Nukleon gewinnt man aber bei der Fusion leichter Atome bzw. der Spaltung schwerer Atome Energie.
Nehmen wir die Kernfusion von 2 Deuteriumatomen zu Helium-3. Die Bindungsenergie pro Nukleon beträgt für Deuterium 1.11 MeV/Nukleon und für Helium-3 genau 2.57 MeV/Nukleon. Um die beiden Deuteriumatome in ihre Einzelbestandteile zu zerlegen ist Energie vonnöten und zwar genau ihre Bindungsenergie. Konkret macht dies also 4 · 1.11 = 4.44 MeV aus.

Beim “Zusammenbau” des Helium-3 Atoms + freies Neutron wird hingegen die Energie 3 · 2.57 = 7.71 MeV frei. In Summe macht dies also einen Energiegewinn von 7.71 – 4.44 = 3.27 MeV pro Fusion aus. Dies mag wenig erscheinen, aber wenn man von sehr großen Fusionszahlen pro Sekunde ausgeht, dann ist die frei werdende Energie bzw. Leistung gewaltig. Die Sonne macht uns dies jede Sekunde deutlich.
Momentan wird in der Physik eifrig an der energiegewinnenden Fusion gearbeitet, so etwa am ITER (International Thermonuclear Experimental Reactor) in Frankreich. Man kann aber eine Kernfusion sogar zuhause realisieren. Benötigt wird hierfür ein sog. Farnsworth-Hirsch-Fusor.
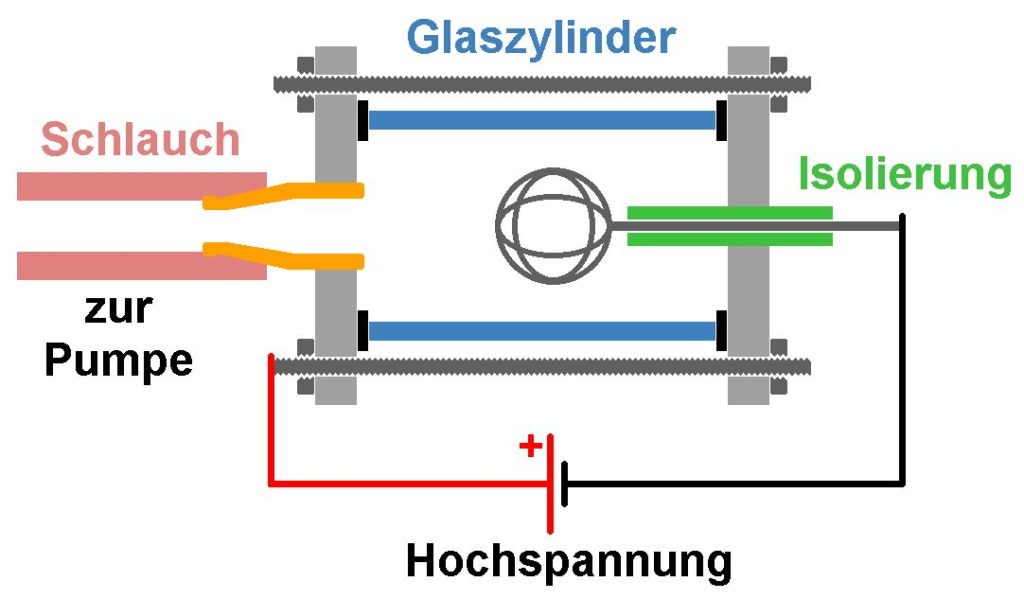
Dieser besteht aus einer Vakuumkammer, wobei das Gehäuse (Pluspol) und eine innere kugelförmige Drahtelektrode (Minuspol) unter Hochspannung (10-40 kV) stehen. Durch Stöße entstehen Ionen und Elektronen. Diese werden im elektrischen Feld beschleunigt und zwar Elektronen nach außen zum Gehäuse und positive Ionen (Kationen) zur inneren Elektrode. Befindet sich innerhalb der Vakuumkammer Deuteriumgas, so besitzen diese nach innen beschleunigten Deuteriumionen eine so hohe Energie, dass sie die Coulombbarriere überwinden können und fusionieren.
Wie weiß man aber nun, ob die Fusion erfolgreich war? Anhand der vorhin erwähnten Reaktionsgleichung wird ersichtlich, dass bei der Fusion zweier Deuteriumatome ein Helium-3 Atom + freies Neutron entsteht. Dieses Neutron ist primärer Träger der frei werdenden Fusionsenergie und kann mit speziellen Neutronendetektoren (siehe auch mein Projekt Neutrongenerator unter Radioaktivität) registriert werden.
Die notwendige Hochspannung erzeuge ich mit einer sog. ZVS-Schaltung und einem Diodensplittrafo (DST) aus einem alten Fernseher.