
Mit Gummibällen habe ich schon als Kind gespielt. Es gibt aber auch einige schöne physikalische Experimente mit ihnen.
Hüpfender Gummiball
Beim ersten Versuch lässt man einen Gummiball ohne Schwung aus einer bestimmten Höhe fallen und bestimmt mit einer Videoanalyse die erzielten maximalen Höhen. Das Programm Tracker (https://physlets.org/tracker/) eignet sich hierfür vorzüglich.


Hat man die maximalen Höhen hi bestimmt, so kann man daraus die jeweiligen Flugzeiten ti von einem Aufprall zum nächsten berechnen. Es gilt:

Das Verhältnis zweier aneinanderfolgender Höhen hi / hi-1 bezeichne ich als q, jenes für die Flugzeiten ti / ti-1 als k:

Zwischen q und k besteht also der einfache Zusammenhang k = √q. Bei jedem Aufprall verliert der Gummiball kinetische Energie. Den Prozentsatz des Energieverlusts berechnet man wiefolgt:

Beträgt also zum Beispiel q = 0.8, so verliert der Gummiball bei jedem Kontakt 20% seiner kinetischen Energie, wenn man den Luftwiderstand unberücksichtigt lässt. Hier mein mit Tracker aufgenommener Höhenverlauf h(t):

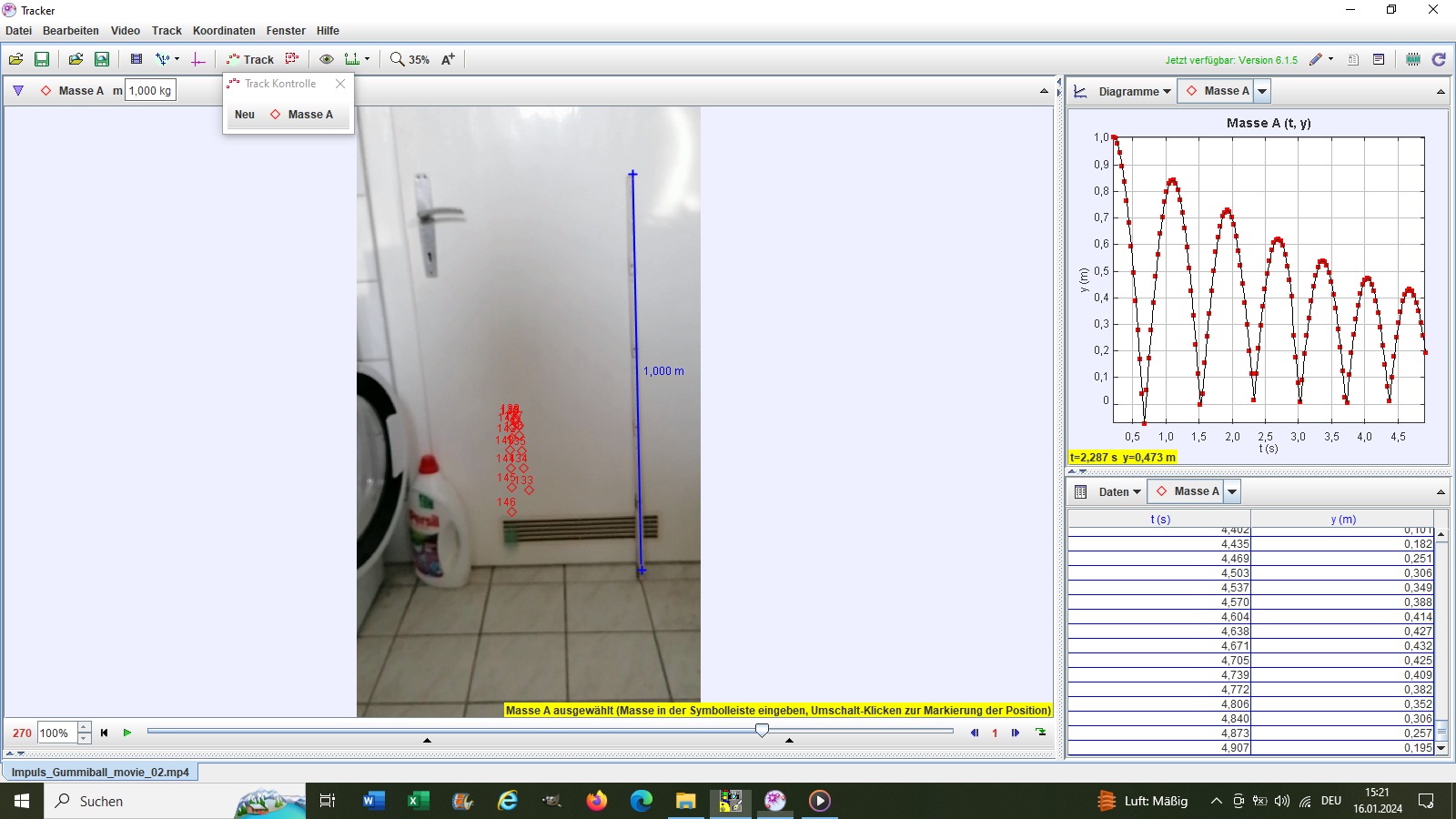

Notiert man sich die maximalen Flughöhen hi, so kann man daraus die prozentuelle Höhenabnahme bestimmen. Bei mir beträgt sie im Schnitt -13%:


Mit diesem Wert kann man die einzelnen Flugzeiten ti ermitteln und diese zur Gesamtzeit tges aufsummieren. Jetzt könnte man meinen, durch die prozentuelle Abnahme der Flugzeiten werden diese zwar immer kleiner, aber ich summiere eine unendliche Anzahl an Zeiten auf. Demnach dürfte der Gummiball niemals zur Ruhe kommen. Dem ist aber nicht so. Selbst die unendliche Summe von (immer kleiner werdenden) Zahlen kann eine endliche Zahl ergeben, wie in diesem Fall. Wir haben es hier konkret mit einer geometrischen Folge zu tun, welche für q < 1 einen endlichen Grenzwert besitzt:
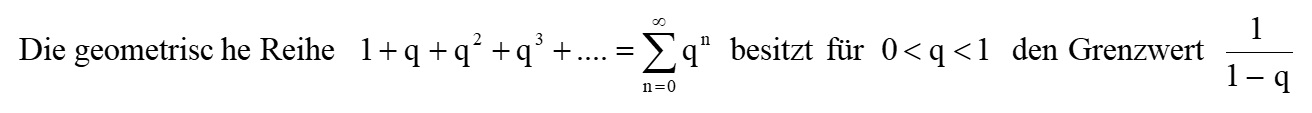
Nutzt man dieses Wissen, kann man die gesamte Flugzeit tges des Gummiballs nun konkret für die 13%ige Abnahme der Flughöhen berechnen:

Nach 13 Sekunden sollte der Gummiball also zum Liegen kommen. Dieser Wert ist durchaus plausibel…
Superspringball
Für den zweiten Versuch benötigt man einen großen und einen deutlich kleineren Gummiball. Diese postiert man in einer bestimmten Höhe h über dem Boden übereinander und lässt beide zeitgleich fallen.

Was wird passieren? Nun, hat man alles richtig gemacht schießt der obere kleine Gummiball mit deutlich höherer Geschwindigkeit nach dem Aufprall nach oben weg. Wie kann dies sein? Woher nimmt er die dafür notwendige Energie?
Die physikalische Herleitung für unterschiedliche Massenverhältnisse mschwer / mleicht ist etwas aufwendiger. Nehmen wir stattdessen ein unendlich großes Massenverhältnis her. Beide Bälle kommen mit der Geschwindigkeit v am Boden an. Der schwere Gummiball wird mit der gleichen Geschwindigkeit -v vom Boden reflektiert. Begeben wir uns nun als Beobachter auf den schweren Ball. Für diesen kommt der leichte Ball mit der Geschwindigkeit 2·v entgegen. Da nun der schwere Ball unendlich schwerer ist als der leichte, wird der leichte mit der selben Geschwindigkeit 2·v vom großen reflektiert und bewegt sich nach oben. Wir befinden uns aber noch immer auf dem schweren Ball und relativ zu diesem bewegt sich der leichte Gummiball mit 2·v nach oben. Da sich der schwere Gummiball aber selbst mit v nach oben bewegt, beträgt nun die Geschwindigkeit des leichten Balls relativ zum Boden 3·v.
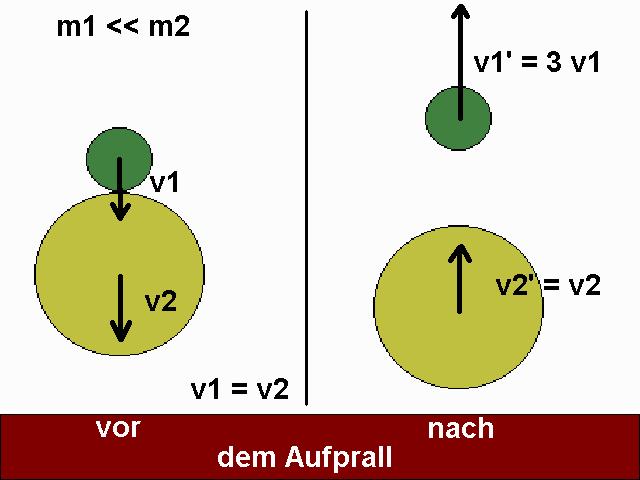
Der kleine/leichte Gummiball saust also mit der dreifachen Aufprallgeschwindigkeit nach oben und besitzt daher die 9-fache kinetische Energie. Er müsste also demnach ohne Energieverluste die 9-fache Ausgangshöhe erreichen. Verblüffend, oder 😉
Ist das Massenverhältnis mschwer / mleicht nicht unendlich, so kommt der kleine Gummiball nicht ganz so hoch. Aber beeindruckend ist es nach wie vor. Die zugenommene kinetische Energie des kleinen Balls stammt natürlich vom großen Gummiball, der dafür nicht mehr ganz die Ausgangshöhe erreicht. Die Superspringbälle hat man einmal im Handel käuflich erwerben können. Derzeit (Stand 2024) habe ich leider kein Angebot für die “AstroBlaster” gefunden. Man kann aber auch einfach selbst zwei Gummibälle besorgen und das Experiment durchführen.

Hat man 3 unterschiedlich schwere Gummibälle (leicht/mittel/schwer) und lässt auch diese übereinander liegend fallen, so kommt der oberste leichte Gummiball sogar noch höher…
Das Experiment konnte ich mit meiner Tochter und meinem Sohn im Hof durchführen. Für einen brauchbaren Versuch bedurfte es dann doch einiger Wiederholungen. Die mit der Software Tracker ermittelte maximale Flughöhe betrug 493 cm bei einer Starthöhe von rund 1.2 m.

Im Video erkennt man, dass wir auch mit shady, dem Hund meiner Tochter, gehörig zu kämpfen hatten 😉
Kraftvoller Gummiball
Lässt man einen Gummiball der Masse m zu Boden fallen, so trifft er mit einer bestimmten Geschwindigkeit v auf. Sein Impuls unmittelbar vor dem Kontakt beträgt also p = m·v. Nach dem Aufprall beträgt seine Geschwindigkeit annähernd noch immer v, nun aber in die entgegengesetzte Richtung und zwar nach oben. Demnach beträgt der Impuls nun p = –m·v. Die Impulsänderung Δp macht demnach den doppelten Impuls aus, nämlich 2·m·v.

Für diese Impulsänderung bedarf es einer Kraft F. Es gilt der einfache Zusammenhang F = Δp / Δt, wobei Δt die Zeitspanne des Kontakts ist. Um diese Kontaktzeit abzuschätzen, verwende ich meine Casio-High speed Kamera. Diese kann Videos mit bis zu 1000 Bildern/sek aufnehmen. Gesagt, getan…
Die Masse des Gummiballs beträgt 34.26 g.



Während des Kontakts wirkt also eine mittlere Kraft von immerhin 71 N, was dem Gewicht von 7 kg entspricht! Den zeitlichen Kraftverlauf könnte ich noch mit meiner Waage für sehr kurze Kraftstöße ermitteln, siehe https://stoppi-homemade-physics.de/kraftmessplatte/.
Stoßexperimente
Mit zwei gleich schweren Gummibällen lassen sich auch folgende Stoßexperimente durchführen. Im ersten Experiment stößt man einen der beiden Bälle auf den anderen, welcher zuvor ruht. Der angestoßene Gummiball bewegt sich dann mit der Geschwindigkeit des ersten davon, während Ersterer stehen bleibt. Dies lässt sich auch theoretisch mittels Impuls- und Energieerhaltungssatz herleiten:




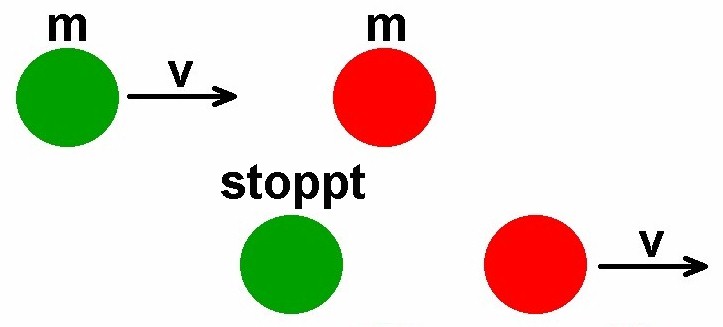

Im zweiten Experiment betrachten wir einen nicht geraden Stoß. Der Gummiball stößt mit dem zuvor ruhenden zweiten Gummiball schräg zusammen. Es geht nun um den Winkel, mit dem die beiden Gummibälle nach dem Stoß auseinanderlaufen.
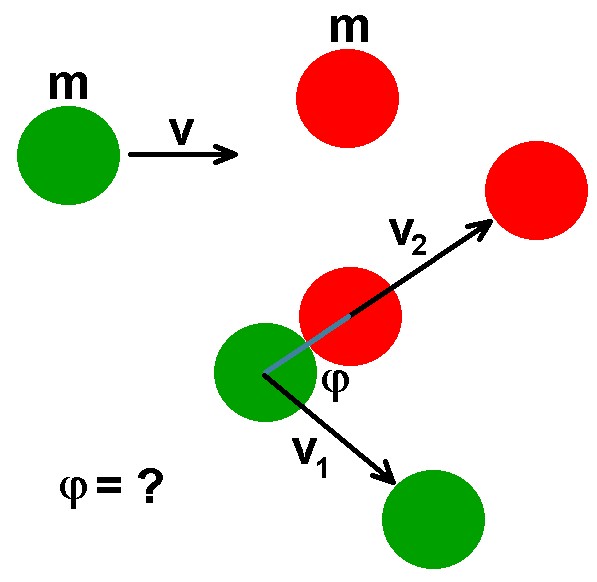

Wie man anhand der theoretischen Herleitung sieht, laufen die beiden Gummibälle im rechten Winkel auseinander (Skalarprodukt der beiden Geschwindigkeitsvektoren = 0). Dies lässt sich auch experimentell leicht überprüfen:


