Wer sich in der Physik ein wenig auskennt, dem ist wohl das Newton’sche Gravitationsgesetz bekannt. Es beschreibt die zwischen zwei Massen m und M im Abstand r wirkende Gravitationskraft (Massenanziehung). Es lautet:
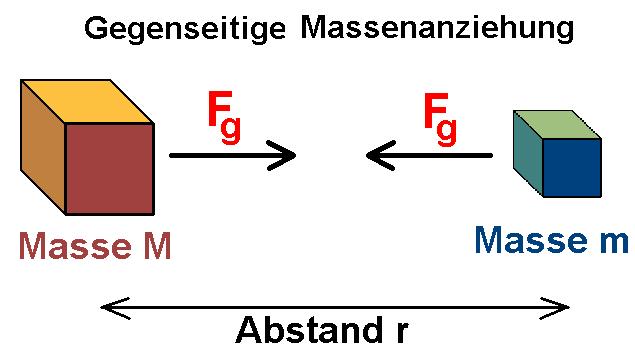

Wie man anhand der Formel erkennen kann entspricht die Gravitationskonstante G (Anm.: nicht zu verwechseln mit der Erdbeschleunigung g) genau der Kraft, die zwischen 1 kg Massen im Abstand von 1 m wirkt. Wie man sich vorstellen kann, ist diese Kraft sehr klein, eben nur 6.67·10^ –11 N. Erst wenn zumindest einer der beiden Körper eine sehr große Masse besitzt, wird die Kraft auch wirklich spürbar. Bestes Beispiel ist unsere Erde, die uns mit der Gravitationskraft (Gewichtskraft) F = m·g ≈ m · 10 anzieht.


Bildquelle: https://de.wikipedia.org/wiki/Henry_Cavendish
Wie konnte man nun solch geringe Kräfte messen? Das erste Experiment zur Bestimmung der Gravitationskonstante G geht auf den britischen Physiker Henry Cavendish (1731 – 1810) zurück. Mit einer sog. Torsions- oder Drehwaage war er im Jahr 1797 imstande, G bis auf 1.2% genau experimentell zu ermitteln. Dabei hängt eine Art Hantel an einem dünnen Torsionsfaden. Nähert man nun den beiden Massen am Ende der Hantelstange zwei weitere, schwere Massen, so müsste sich die Hantel aufgrund der Massenanziehung geringfügig verdrehen. Aus dieser minimalen Verdrehung lässt sich in weiterer Folge die Kraft zwischen den Massen und daher auch die Gravitationskonstante G ermitteln.
Zum Verdrehen des Torsionsfadens um den Winkel φ benötigt man ein Drehmoment T = R·φ (R…Richtmoment). Lässt man das Torsionspendel aus, so vollführt es Drehschwingungen mit einer bestimmten Periodendauer τ. Diese Periodendauer hängt von R und vom Trägheitsmoment I des am Torsionsfaden aufgehängten Körpers ab. Je größer quasi die Rückstellkraft R, desto schneller schwingt das Torsionspendel. Je träger der Körper (großes I), desto langsamer. Die Formel für die Periodendauer lässt sich recht einfach wiefolgt herleiten:

In diesem Experiment wird es unter anderem um die Bestimmung des Richtmoments R mittels der Periodendauer gehen. Laut Formel muss zur Bestimmung von R auch das Trägheitsmoment I des aufgehängten Körpers bekannt sein. Hier eine Tabelle mit den Trägheitsmomenten einiger einfacher Körper:

Bildquelle: https://de.wikipedia.org/wiki/Trägheitsmoment

Quelle: www.johannes-strommer.com

In meinem Fall entspricht der am Torsionsfaden aufgehängte Körper einer Hantel. Die beiden Kugeln am Ende der Hantelstange besitzen die Masse mK und den Radius rK. Die Stange zwischen den beiden Massen besitzt die Masse mS, den Innenradius rSi, den Aussenradius rSa und die Länge LS. Damit und dem Satz von Steiner lässt sich das Trägheitsmoment I der Hantelstange bestimmen.



Das Messingrohr mit genügend Wandstärke (1mm) habe ich auf Amazon gefunden:








Hier der am Messingrohr festgelötete Kupferlackdraht:

Die obere Drahtfixierung habe ich mit zwei Alu-L-Winkel gelöst:


Als Träger für das Torsionspendel verwende ich mein Fotostativ. Dieses besitzt am Boden einen ausreichenden Abstand der Beine, sodass sich das Pendel ungestört drehen kann:



Hier nun das berechnete Trägheitsmoment I, welches zusammen mit der Periodendauer τ das Richtmoment R ergibt:
Kennt man nun das Richtmoment R des Torsionsfadens, so kennt man das zum Verdrehen um den Winkel φ notwendige Drehmoment T. Dies werden wir gleich noch benötigen. Nähert man nämlich der Hantelstange zwei weitere Massen M, so wirkt primär zwischen diesen Massen und den beiden Hantelmassen die Gravitationskraft FG. Mittels dieser Kraft kann nun das wirkende Drehmoment T = Kraft · Kraftarm bestimmt werden.
Als Massen M kommen meine beiden Fernrohrgewichte zum Einsatz. Diese besitzen eine Masse von je 3.14 kg:




Dies sieht ja alles sehr überschaubar aus. Die Schwierigkeit liegt zum einen im sehr geringen Ablenkwinkel φ und zum anderen an den vielen, möglichen Störungen. Das Torsionspendel wird nicht still stehen, sondern langsame Schwingungen vollführen. Es gilt dann quasi den Mittelwert dieser Schwingungen ohne und mit Massen M zu ermitteln.
Mit bekannter Gravitationskonstante G lässt sich der zu erwartende Drehwinkel abschätzen:


Das Ergebnis ist ziemlich ernüchternd. Nur 1.8 mm Verschiebung des Laserpunkts auf einer 3 m vom Torsionsfaden entfernten Skala. Ich werde daher wohl einen noch dünneren Wolframdraht besorgen müssen. Diesen gibt es zum Beispiel auf ebay aus der Ukraine:


Ich habe mir gerade die Werte für die Zugfestigkeit von Kupfer bzw. Wolfram angeschaut.
Kupfer: Zugfestigkeit 250 MPa = 250 N/mm²
Wolfram: Zugfestigkeit 550 – 1920 N/mm²
 Quelle: https://www.materialmagazin.com/index.php/ne-metalle/eigenschaften-und-gewinnung-von-kupfer
Quelle: https://www.materialmagazin.com/index.php/ne-metalle/eigenschaften-und-gewinnung-von-kupfer

Quelle: https://de.wikipedia.org
Bei Verwendung des 0.1 mm Kupferdrahts (A = 0.00785 mm²) und einer Belastung mit 290 g (= 2.9 N) komme ich bereits auf eine Spannung von 369 N/mm². Da bin ich bereits deutlich über der Zugfestigkeit von Kupfer…
Wenn ich nun einen Wolframdraht mit 2.9 N belaste, komme ich auf folgende Spannungen:
0.08 mm Wolframdraht: Spannung = 577 N/mm²
0.065 mm Wolframdraht: Spannung = 874 N/mm²
Da bin ich ggf. auch schon über der Zugfestigkeit. Ich werde daher wohl beide Drähte aus der Ukraine bestellen und schauen, wie/ob es funktioniert.
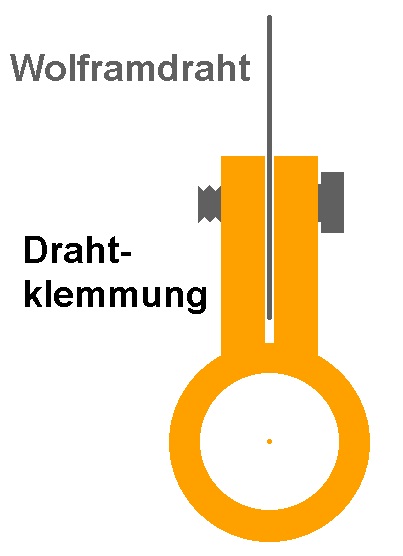
Da man Wolframdraht nicht mit dem normalen Lötkolben verlöten kann, habe ich mir eine einfache Klemmung ausgedacht. Dazu habe ich einfach 2 dünne Messingplatten auf das Messingrohr gelötet. Dazwischen spanne ich dann den Wolframdraht ein. Getestet habe ich die Konstruktion mit dem 0.1 mm Kupferlackdraht und es funktioniert sehr gut.



Zur bequemeren und vor allem störungsfreien Beobachtung/Aufzeichnung des Laserpunkts an der Wand vom Nachbarraum aus habe ich mir eine gebrauchte Logitech-Webcam für nur 10 Euro gekauft. Dasselbe Modell kommt schon in meinen Webcam-Spektroskopen zum Einsatz und ich bin mit der Bildqualität mehr als zufrieden. Sie besitzt 2 Megapixel und ein Zeiss-Objektiv.


In meinen Unterlagen zum Einstein-de Haas-Versuch hatte ich für das Richtmoment eines Nylondrahts mit 0.3 mm Durchmesser 10^-6 notiert. Dies würde doch deutlich unter jenem des 0.1 mm Kupferlackdrahts liegen. Daher habe ich einmal die Periodendauer mit der Nylonschnur bestimmt und ich komme auf τ = 902 sek. Damit errechnet sich ein Richtmoment von nur 1.145 · 10^ –6 Nm/rad.
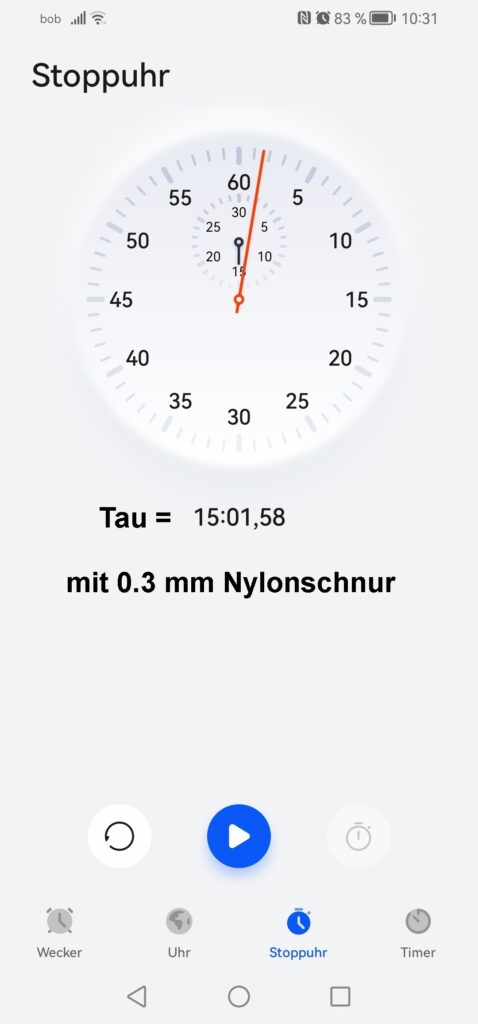

Bei einem solchen Richtmoment sollte die Ablenkung des Laserpunkts auf einer 3 m entfernten Skala bereits 11 mm betragen:
Da mich dies zuversichtlich stimmte, wagte ich mit der Nylonschnur einen ersten Versuch zur Messung der Gravitationskonstante G.




Das Ergebnis war aber ernüchternd. Das Pendel schwingte selbst nach Stunden des Wartens noch immer viel zu stark. Die Schwingungsamplitude betrug dann noch immer gute 20°, sodass der Laserpunkt in keinster Weise auf der Skala ruhte. Das Problem ist auch die sehr große Periodendauer von mehr als 10 Minuten. Bei einer geringen Dämpfung an Luft müsste ich schon rein theoretisch mehrere Stunden warten, bis sich das Pendel beruhigt hat. In der Praxis gibt es aber selbst dann noch immer Störeinflüsse, die eine Ruhe verhindern.
Video des vorbeirasenden Laserpunkts auf der Skala nach mehr als einer Stunde Wartezeit im Nebenraum ohne sichtbare Störung des Pendels:
So wird das nichts werden. Ich habe mir daher eine viel stärkere Dämpfung überlegt. Eine Messingfinne soll unterhalb des Pendels in ein Wasserbad ragen und dadurch in der Bewegung stark gedämpft werden. Als Profil dachte ich an einen doppel-T-Träger, sodass auch Bewegungen hinein und hinaus unterbunden werden.
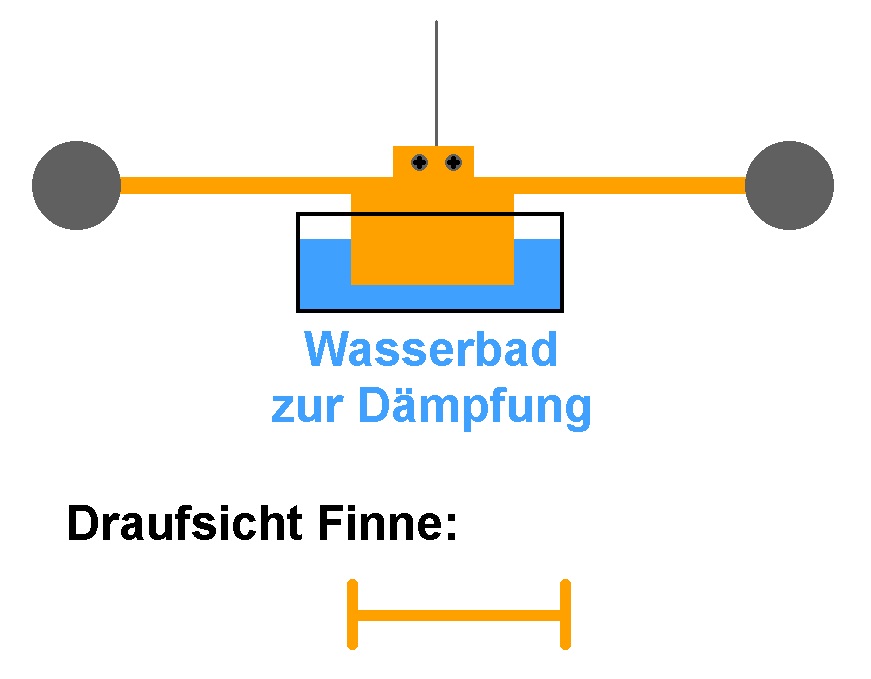
Grundvoraussetzung für die Messung der Gravitationskonstante G ist eine wirklich stabile Ruhelage des Pendels bzw. maximal Schwingungen im Bereich der 21 cm langen Skala. Erst dann kann ich die beiden großen Massen hinzufügen und die neue Ruhelage bestimmen. Wie schon erwähnt liegt die erwartete Verschiebung des Laserpunkts auf der Skala im Bereich von nur 10 mm. Da macht es keinen Sinn, wenn der Laserpunkt noch mehrere Meter hin und herschwingt.
Nach diesen Problemen habe ich die allergrößte Hochachtung vor der Leistung von Henry Cavendish bzw. anderer Experimentalphysiker. Ein Experiment lässt sich im Unterricht sehr einfach erörtern bzw. darstellen. Welche Schwierigkeiten dann real auf einen zukommen, wissen die wenigsten. Wie H. Cavendish Ende des 18. Jahrhunderts die Gravitationskonstante G auf 1.2 % genau bestimmen konnte ist für mich ein Wunder bzw. eine Glanzleistung ersten Ranges.
Hier die fertige Messingfinne:



Ich konnte heute die Finne ausprobieren und ja, sie dämpft. Aber……der Laserpunkt wandert, nun zwar langsamer und mit geringerer Amplitude aber auch nach langer Wartezeit noch immer aus der Skala hinaus. Als Flüssigkeit habe ich Rapsöl verwendet.



Video: Cavendish_movie_Öl_04
Da also die Aufzeichnung der Schwingungen mittels Laserstrahl fehlgeschlagen ist, postiere ich nun die Webcam oberhalb des Pendels. Damit kann ich zwar die Bewegungen massiv grober nur aufzeichnen, aber ich erfasse zumindest den gesamten Bewegungsablauf.



Ich werde nun also über 1 bis 1.5 Stunden die Schwingungen ohne und mit hinzugefügten Massen aufzeichnen. Ich bin mir aber dessen bewusst, dass eine Winkelabweichung ohne/mit Massen theoretisch so nicht zu messen ist, da viel zu gering. Auf Youtube sieht man allerdings fast in allen Videos Winkeländerungen im Grad-Bereich, was so nicht stimmen kann. Bei einer Kraft von 3.5·10^ –9 N, einem Richtmoment von 7·10^ –6 Nm/rad und einer Hantellänge von 60 cm sollte die Winkelablenkung durch die Massen im Bereich von nur 0.0172° liegen (Rechnung siehe oben), also so mit einer Webcam mit Sicherheit nicht feststellbar. Aber dann hätte ich wenigstens ein Messergebnis, welches sich interpretieren ließe… 😉
Heute konnte ich die Messreihen durchführen. Einmal 1.5 Stunden ohne Massen und dann 1.5 Stunden mit Massen in die eine Richtung und 0.5 Stunden in die andere Richtung. Das Torsionspendel folgte dabei sehr schön den Massen aber leider viel zu stark.



Ich konnte eine Winkeländerung von ganzen 6° bestimmen.



Bei einem Abstand der Massen von 5 cm zueinander komme ich mit diesen Werten auf eine Gravitationskonstante G = 8.7·10^ –9 m³/kg·s². Der Sollwert ist gut 100mal kleiner und beträgt G = 6.67·10^ –11 m³/kg·s².

Ehrlich gesagt kann ich mir die viel zu starke Ablenkung nicht erklären. Eventuell spielt eine elektrostatische Aufladung eine Rolle. Eigenartigerweise zeigen aber auch sehr viele Youtube-Videos eine viel zu große Gravitationswirkung wie bei mir. Naja, immerhin kam es zu einer Massenanziehung und nicht Abstoßung 😉
Kurzer Nachtrag: Die beiden Wolframdrähte mit 65 µm und 80 µm Durchmesser sind ohne Probleme aus der Ukraine bei mir eingetroffen. Möge dieser schreckliche Krieg bald zu Ende sein und es nicht noch zu mehr Blutvergießen kommen 🙁

Den Versuch habe ich mit diesen beiden Drähten nochmals wiederholt. Der 0.065 mm Draht riss immer wieder noch beim Festmachen der Hantel. Mit dem 0.08 mm Draht ging es dann besser, aber ich erhielt noch mehr störende Schwingungen als mit dem 0.1 mm Kupferdraht. Da das Pendel selbst nach mehr als einer Stunde nicht einmal eine definierte Ruhelage besaß war ich nicht imstande, eine Winkeländerung mit hinzugefügten Massen zu beobachten. Von daher muss ich wohl dieses Experiment zu den Akten legen. Vielleicht ist die Messumgebung inmitten eines Wohnhauses in einer Großstadt auch einfach zu unruhig für diesen Versuch…
Das Youtube-Video reiche ich wie immer nach…
Ich durchstreife ja verschiedene Verkaufsplattformen immer wieder einmal auf der Suche nach neuen Physikprojekten. Neulich bin ich auf Kleinanzeigen dann per Zufall auf die Verkaufsanzeige einer Gravitationswaage nach Cavendish gestoßen. Inseriert war das gute Stück um 125 Euro noch ohne Versand. Der Verkäufer machte mir aber ein unwiderstehliches Angebot, welches ich nicht ausschlagen konnte. Normalerweise kaufe ich keine kommerziellen Fertigprodukte, denn ich möchte meine Physikprojekte ja weitestgehend selbst basteln und umsetzen.

Die Gravitationswaage kam bestens verpackt und wohlbehalten bei mir an, vielen lieben Dank nochmals für alles an den Verkäufer Karl-Heinz 😉










Da die beiden schweren Massen fehlten (dies stand auch so in der Verkaufsanzeige) musste ich mich nach möglichst schweren Metallkugeln umsehen. Aus Blei (Dichte ρ = 11.34 g/cm³) waren aber leider keine zu einem vernünftigen Preis zu finden, daher kaufte ich schließlich zwei 70 mm messende Kugeln aus Stahl (Dichte ρ = 7.85 g/cm³).

Hier die Herleitung zur Bestimmung der Gravitationskonstante G:



Wenn es Neuigkeiten gibt, geht es hier weiter…

