Ein Körper mit einer bestimmten Temperatur T strahlt elektromagnetische Strahlung ab. Dies bemerkt man zum Beispiel in einer Schmiede, wenn das Eisenstück auf eine hohe Temperatur gebracht wird. Das Spektrum jener Strahlung war um das Jahr 1900 herum bereits bekannt, nur konnte man es nicht zufriedenstellend theoretisch herleiten.
Zwei vorhandene theoretische Näherungen scheiterten, den Intensitätsverlauf dieser Wärmestrahlung vollständig zu beschreiben. Während das Rayleigh-Jeans-Gesetz nur für große Wellenlängen (niedrige Frequenzen) mit den experimentellen Ergebnissen übereinstimmte und für steigende Frequenzen die sog. Ultraviolettkatastrophe vorhersagte, sagte das Wiensche Strahlungsgesetz den richtigen Intensitätsverlauf nur für kleine Wellenlängen (große Frequenzen) voraus.
Der deutsche Physiker Max Planck widmete sich dieser theoretischen Herausforderung der sog. Schwarzkörperstrahlung. Er postulierte, dass elektromagnetische Strahlung nur in Energieportionen E = h · f = h · c / λ abgegeben werden kann. Dies kann man als Geburtsstunde der Quantenphysik bezeichnen. Unter dieser Annahme erhielt er einen zu erwartenden Intensitätsverlauf, welcher ausgezeichnet mit den experimentellen Ergebnissen übereinstimmte.
Die von ihm hergeleitete Formel für den spektralen Intensitätsverlauf lautet:
M_0_λ(λ, T) ist die Strahlungsleistung, die vom Flächenelement dA im Wellenlängenbereich zwischen λ und λ + dλ in den gesamten Halbraum abgestrahlt wird. Neben der Wellenlänge λ hängt der Intensitätsverlauf von der Temperatur T ab:
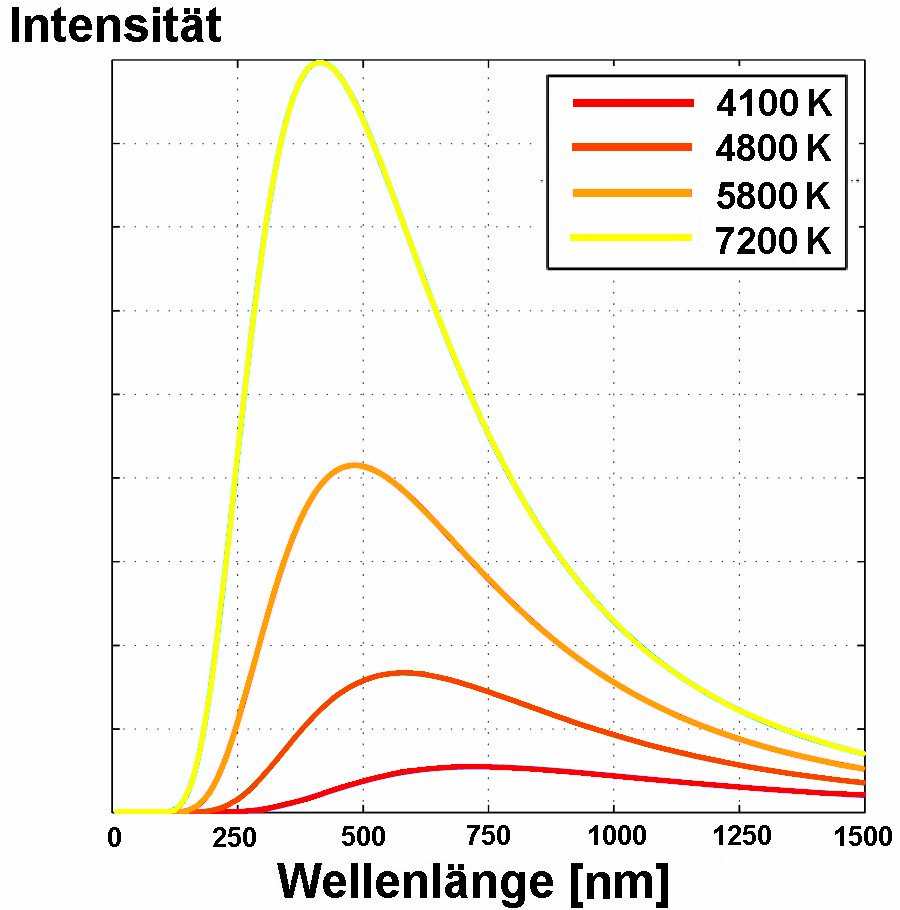
Was erkennt man anhand obiger Spektren? Je höher die Temperatur T, desto weiter verschiebt sich das Strahlungsmaximum nach links in Richtung kleinerer Wellenlänge. Bei einer Temperatur von zum Beispiel 5800 K liegt das Strahlungsmaximum bei einer Wellenlänge von ca. 500 nm. Dies entspricht auch etwa dem Intensitätsverlauf unserer Sonne. Deren Oberflächentemperatur muss daher auch in diesem Bereich liegen. Die einfache Beziehung zwischen λmax und Temperatur T beschreibt das Wien’sche Verschiebungsgesetz, welches lautet:
λmax [in μm] = 2897,8 / T [in K]
Man erkennt aber auch, dass die Fläche unter der Kurve mit zunehmender Temperatur stark zunimmt. Die Fläche unter dem Intensitätsverlauf entspricht der über alle Wellenlängen abgestrahlten Energie pro Sekunde und Quadratmeter, also der gesamten Strahlungsintensität.
Hierfür fanden die beiden österreichischen Physiker Josef Stefan und Ludwig Boltzmann eine einfache Beziehung, welche lautet:
Iges = σ · T^ 4 mit σ = Stefan-Boltzmann-Konstante = 5.67 · 10^ –8 W/m² · K^ 4
Ein Körper mit doppelter Temperatur strahlt demnach insgesamt die 16-fache Energie pro Sekunde und m² ab.
Bildquellen:
https://de.wikipedia.org/wiki/Ludwig_Boltzmann#/media/Datei:Boltzmann2.jpg
https://de.wikipedia.org/wiki/Josef_Stefan#/media/Datei:Jozef_Stefan.jpg
Das Stefan-Boltzmann-Gesetz lässt sich auf folgende zwei Arten experimentell überprüfen:
Variante 1:
Bei dieser Variante wird die von einer Glühbirne der Temperatur T abgestrahlte Leistung mit einer sog. Thermosäule gemessen. Dazu wird die Glühbirne in einem bestimmten Abstand vor der Thermosäule postiert und dann die Glühbirnenspannung U langsam erhöht. Sodann misst man die von der Thermosäule erfasste Strahlungsleistung P in Abhängigkeit von der Glühbirnenspannung U.
Kennt man die Spannung U und den Strom I durch die Glühbirne, lässt sich sehr einfach der Widerstand R = U / I der Wolframglühwendel berechnen. Dieser Widerstand R ist aber abhängig von der Temperatur T der Glühwendel. Es gilt:
Ich verwende konkret für diesen Versuch eine 12V/5W Glühbirne mit dem Widerstand bei Raumtemperatur, sprich ohne anliegende Spannung, R20°C = 3 Ω.
Kennt man nun das Widerstandsverhältnis R / R20°C, so kann man mit obiger Formel sehr einfach die Temperatur der Glühwendel berechnen. Der zugehörige Graph T(R) sieht wiefolgt aus:
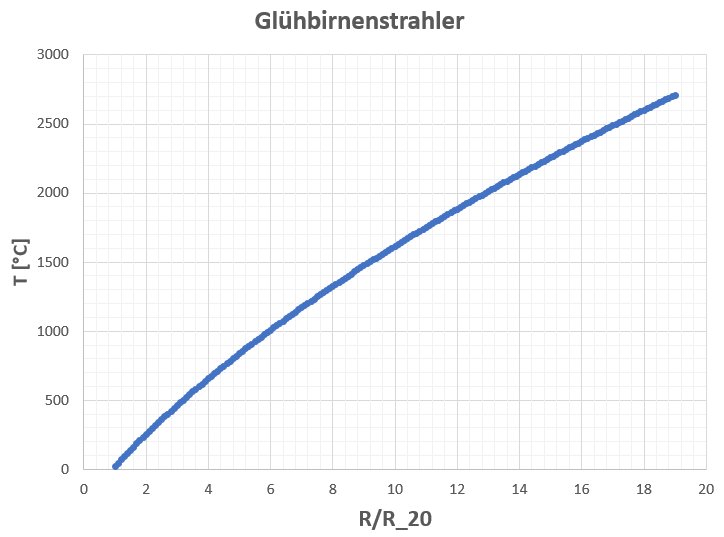
Hier die von mir gebastelte Thermosäule (https://stoppi-homemade-physics.de/thermosaeule/), mit der man die Strahlungsleistung bestimmen kann:
Die Schaltung zur variablen Ansteuerung der Glühbirne sieht wiefolgt aus:
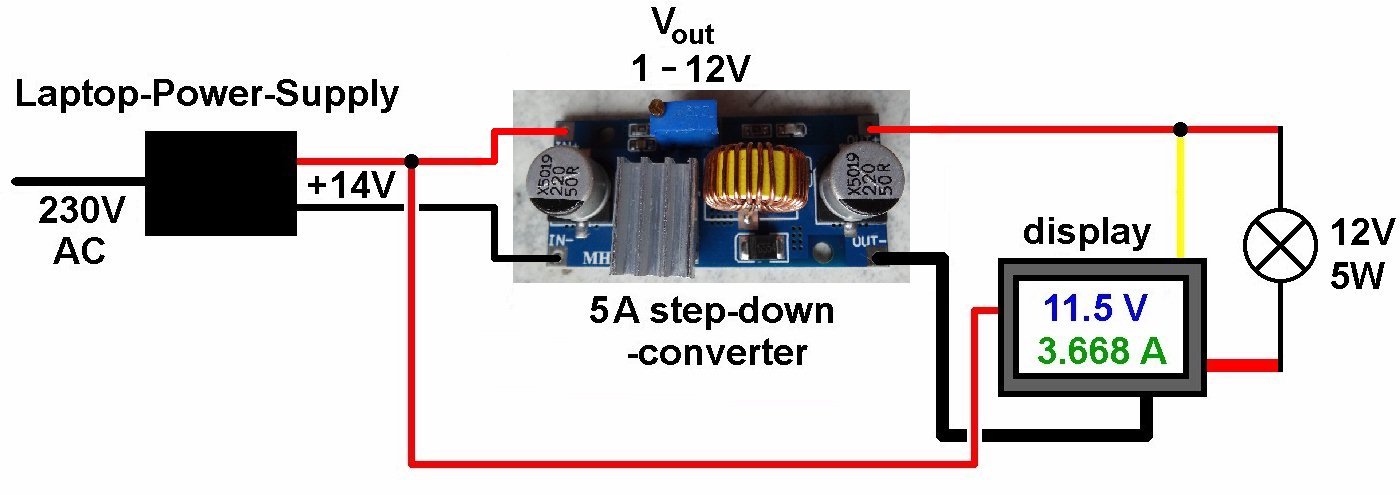
Diese Teile wurden dabei konkret verbaut:
Zur bequemeren und genaueren Einstellung der Glühbirnenspannung U dient ein 10-Gang Potentiometer mit 50 kΩ:
Zur Anzeige von U und I verwende ich dieses günstige 4-digit-Panelmeter aus China:
Hier nun der fertige Glühbirnen-Aufbau:
Hier nun der finale Aufbau des Experiments:
Besitzt die Glühbirne noch Raumtemperatur T = 293 K, sprich liegt noch keine Spannung U an ihr an, so zeigt die Thermosäule natürlich auch keine Strahlungsleistung P an. Daher muss man P in Abhängigkeit von T^ 4 – TRaum ^ 4 auftragen! Stimmt das Stefan-Boltzmann-Gesetz, so ist ein linearer Verlauf von P in Abhängigkeit von T^ 4 – TRaum ^ 4 zu erwarten.
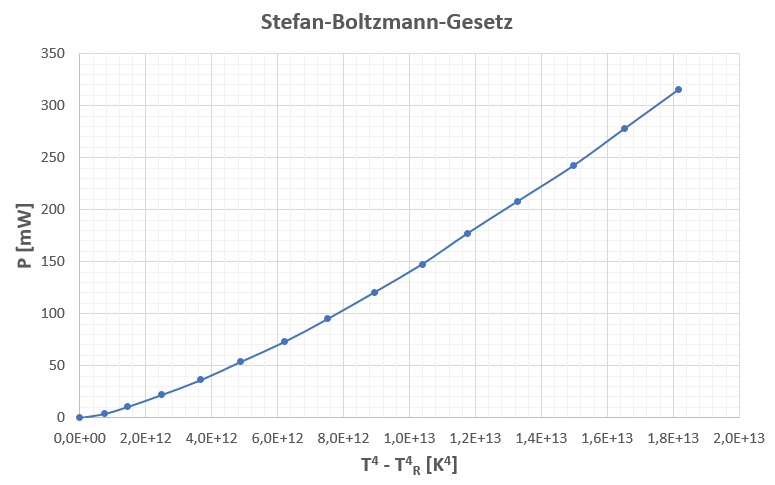
Wie man sieht, erhält man (fast) einen linearen Zusammenhang zwischen der mit der Thermosäule erfassten Strahlungsleistung und der 4-ten Potenz der Temperatur T. Somit gilt das Stefan-Boltzmann-Gesetz einigermaßen als bewiesen.
Variante 2:
Hat man keine Thermosäule zur direkten Messung der von der Glühbirne abgegebenen Strahlungsleistung zur Verfügung, so kann man auch stattdessen einfach die der Glühbirne zugeführte elektrische Leistung P = U · I in Abhängigkeit von T^ 4 – TRaum ^ 4 auftragen. Denn bei einem Gleichgewicht muss die der Glühbirne zugeführte elektrische Leistung der abgegebenen Strahlungsleistung entsprechen!
Wie man erkennen kann, ergibt sich wieder ein (fast) linearer Zusammenhang, Stefan-Boltzmann lässt grüßen…
Nochmals das Stefan-Boltzmann-Strahlungsgesetz: P = σ · A · (T ^4 – TRaum ^4). Trägt man also P gegen T ^4 – TRaum ^4 auf, so ergibt sich eine Gerade mit der Steigung k = σ · A.
Konkret erhalte ich mit meinen experimentellen Werten einen Anstieg von k = 3.19 · 10 ^–13 W/K ^4.
Um aus dem bekannten Anstieg k = σ · A die Stefan-Boltzmann-Konstante σ zu bestimmen, benötigt man die Oberfläche A der Glühwendel. Um diese zu ermitteln, messe ich zunächst den ohmschen Widerstand R der Glühbirne bei Raumtemperatur. Dazu baue ich eine einfache Serienschaltung bestehend aus Vorwiderstand und Glühbirne auf:
Ich komme auf einen Wert von 2.98 Ohm. Die Formel für den Widerstand eines Drahts lautet:
Vom Wolframdraht kenne ich nun den Widerstand R und den spezifischen Widerstand ρ. Den Radius r ermittle ich mit dem Mikroskop meiner Tochter. Dazu vergleiche ich die Drahtdicke mit einer 10 µm-Skala:
Die Bilder messe ich mit meinem uralten und simplen Grafikprogramm aus:
Ich komme also auf einen Drahtradius r = 20.7 µm. Damit lässt sich jetzt die Drahtlänge ableiten:
Das Ergebnis erscheint durchaus plausibel. Wir benötigen ja zur Bestimmung der Stefan-Boltzmann-Konstante σ die Drahtoberfläche. Für diese gilt:
Jetzt sind wir fast fertig:
Mein experimentell ermittelter Wert für σ weicht doch ein wenig vom Sollwert ab. Ich gebe aber zu bedenken, dass etwa der mit dem Mikroskop gemessene Drahtradius fehlerbehaftet ist, da sich Draht und Skala nicht in derselben Ebene unter dem Mikroskopobjektiv befanden. Und der Radius r geht zum Quadrat in die Formel für den ohmschen Widerstand R des Drahts ein, sodass sich ein Messfehler noch stärker auswirkt. Ein etwa zu groß gemessener Radius ergibt demnach eine noch deutlicher zu große Drahtlänge. Und beide gehen ja dann direkt proportional in die Formel zur Berechnung der Drahtoberfläche ein. Die dann viel zu große Drahtoberfläche würde eine viel zu geringe Stefan-Boltzmann-Konstante bedingen.
Den Versuch kann ich aber nur wärmstens empfehlen, da man mit sehr wenig Geld in die Welt der Quantenphysik eintauchen kann und sich mit σ sogar eine berühmte Konstante berechnen lässt. 😉
Das Youtube-Video reiche ich wie immer nach…
