Nanoleiter, also atomar betrachtet annähernd 1-dimensionale Leiter haben faszinierende Eigenschaften, die man mit der klassischen Physik nicht erklären kann. So ist der Leitwert G (also der inverse Widerstand 1/R) eines Leiters mit atomarer Dicke nicht beliebig und durch seinen spezifischen Widerstand, dessen Länge und der Querschnittfläche bestimmt, sondern gequantelt.

Links:

• https://physicsopenlab.org/2020/03/18/observing-quantized-conductance-in-a-normal-relay/
• https://docplayer.org/41378856-Quantisierung-des-leitwerts-in-eindimensionalen-goldkontakten.html

Nanoleiter entstehen zum Beispiel bei einem sich öffnenden Kontakt. Der Durchmesser der Nanoleiter beträgt oft nur 2-10 nm.

Bildquelle: PLUS LUCIS 2/97; https://docplayer.org/41378856-Quantisierung-des-leitwerts-in-eindimensionalen-goldkontakten.html

Um die quantenmechanischen Vorgänge in solchen Nanoleitern erfassen zu können, bedient man sich eines möglichst einfachen Modells. In diesem Fall ist dies der Potentialtopf mit unendlich hohen Wänden. Ein solcher, unendlich tiefer Potentialtopf besitzt das einfache Potential

Die Schrödingergleichung lautet allgemein

In den beiden äußeren Bereichen ist konkret V(x) = ∞. Daher muss dort die Wellenfunktion verschwinden, also Ψ(x) = 0 gelten. Durch die geforderte Stetigkeit der Wellenfunktion muss an den Rändern des Potentialtopfs weiters gelten: Ψ(x = 0) = 0 und Ψ(x = L) = 0. Für den Bereich innerhalb des Potentialtopfs lautet durch V(x) = 0 die Schrödingergleichung:

Wir setzen als Lösungsfunktion Ψ(x) an:

Eingesetzt in die Differentialgleichung liefert dies folgende Bedingung für k:

Die allgemeine Lösung für den inneren Bereich lautet also

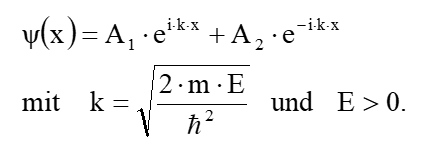
Jetzt gilt es auch noch die Stetigkeitsbedingungen Ψ(x = 0) = 0 und Ψ(x = L) = 0 zu erfüllen. Daraus folgt:

Die vollständige Wellenfunktion lautet also für den Bereich innerhalb des Potentialtopfs:

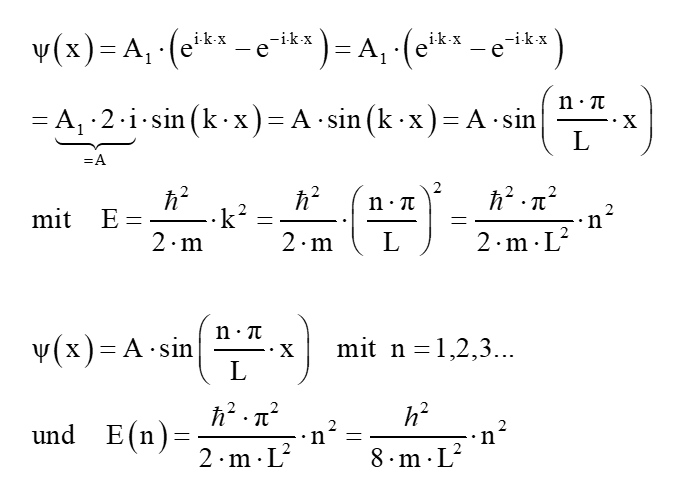
Wie sehen nun diese Lösungen der Wellenfunktion aus?

Man sieht anhand der Formel für die erlaubten Energien auch schön den Unterschied zwischen Quantenwelt und der klassischen Physik. In der Quantenwelt geht es um sehr kleine Abmessungen, zum Beispiel die Ausdehnung L des Potentialtopfs. Die klassische Physik behandelt viel größere Objekte. Wächst aber nun die Größe des Drahts L an, so liegen die erlaubten Energiezustände viel enger beisammen (vgl. E(n) = 1/L²) und es entsteht ein Quasikontinuum (siehe Abbildung weiter unten). In der klassischen Physik darf nämlich zum Beispiel ein Elektron sämtliche Energien annehmen und es existiert keine Quantelung.

Formen wir nun die Formel für die Energie nach n um und erhalten

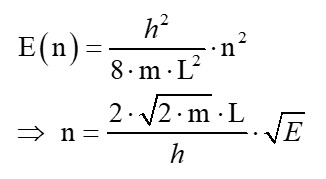
Setzt man für E eine bestimmte Energie ein, erhält man n, also die Anzahl der möglichen Zustände mit einer Energie ≤ E. Differenziert man nun die Funktion n(E) nach E, erhält man quasi die Dichte der Zustände. Dies ergibt:

Diese Zustandsdichte nimmt mit zunehmender Energie ab, da die Abstände der einzelnen Zustände mit zunehmender Energie wie abgebildet zunehmen.

Setzt man für E den Ausdruck der kinetischen Energie ½ · m · v² ein, erhält man für die Zustandsdichte

Zwischen den Enden des Nanodrahts, durch den ein bestimmter Strom fließt, liegt ja eine elektrische Spannung U an. Die beiden Bereiche an den Enden des Nanodrahts sind also unterschiedlich hoch aufgefüllt. Bei einer elektrischen Spannung U beträgt der Energieunterschied für die Elektronen mit der Ladung e genau e·U.

Wie viele Elektronen tragen nun zum Stromtransport im Nanodraht bei? Wir kennen ja die Zustandsdichte dn/dE. Daraus ergibt sich für die Anzahl an Zuständen innerhalb der Energie e·U der Ausdruck

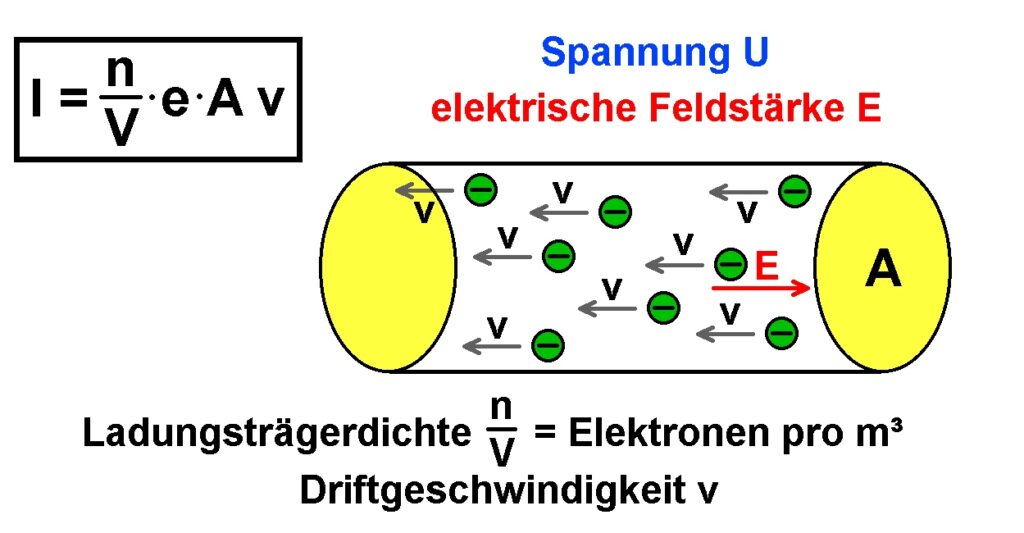
Für die Stromstärke I in einem Leiter gilt aber auch der Ausdruck:

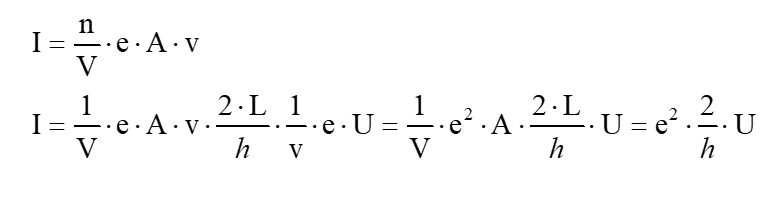
Setzt man nun für den Ausdruck I/U = 1/R den Leitwert G ein ergibt sich schlussendlich für G

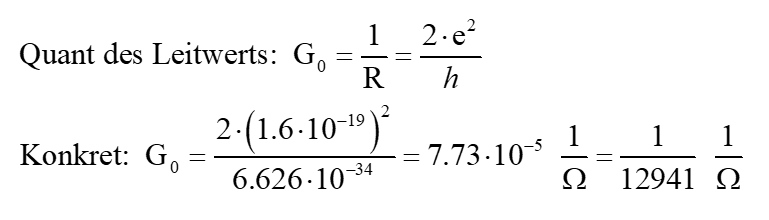
Der Leitwert G ist also für einen Nanoleiter eine konstante Größe, also gequantelt. Der gesamte Leitwert aufgrund mehrerer paralleler Nanoleiter ergibt sich also als Vielfaches dieses Leitwerts. Durch die Quantelung des Leitwerts können bei einer an den Nanoleitern anliegenden Spannung auch nur gequantelt Ströme fließen.

Nanoleiter kommen etwa bei einem sich öffnenden Relais vor. Liegt eine Spannung U von zum Beispiel 10 mV am Relais an, so fließt beim Öffnen durch die gequantelten Leitwerte der entstehenden Nanoleiter nur abnehmender, gequantelter Strom. Der Stromverlauf muss also Stufen aufweisen.

Bildquelle: https://physicsopenlab.org/2020/03/18/observing-quantized-conductance-in-a-normal-relay/

Mit einem Transimpedanzverstärker (TIA) wird der geringe Strom in eine Spannung umgewandelt und mit dem Oszilloskop aufgezeichnet. Der Verstärkungsfaktor liegt durch den 100 kOhm-Widerstand im Feedbackzweig bei 10^5. Als Operationsverstärker verwende ich den OPA354:

Welche Spannungsstufen sind am Oszilloskop zu erwarten?

Nehmen wir an, der Spannungsteiler liefert am Ausgang eine Spannung von 10 mV. Wie wir oben gesehen haben, kann der Leitwert des sich öffnenden Relais nur Vielfache von G₀ = 1/12941 Ohm annehmen. Für die Stromstärke folgt daraus:

Die am Oszilloskop sichtbaren Spannungsstufen müssten also bei einer Spannung von 10 mV rund 77 mV betragen. Verdoppelt man die Spannung auf 20 mV, so müssten auch die Stufen doppelt so groß sein, nämlich 154 mV.

Die Operationsverstärker und die dazupassenden Adapterplatinen sind soeben aus China eingetroffen. Hoffentlich handelt es sich bei den Chips nicht um fake-Produkte. Also ich muss sagen, viel kleineres als SOT23 könnte ich nicht mehr löten. Da benötigt es schon eine ruhige Hand. Die Kontakte scheinen aber alle zu passen (mit dem Durchgangsprüfer am Multimeter getestet).

In der Zwischenzeit konnte ich die einfache Schaltung mit dem Relais aufbauen und erstmalig testen. Die Ergebnisse sind nicht vollends befriedigend. Ich erhalte zwar immer wieder einmal Stufen in der fallenden Flanke, aber dies eher in Ausnahmefällen bzw. nicht sehr deutlich ausgeprägt.

Zu beachten ist die negative Spannungsversorgung des Spannungsteilers! Mit einer positiven Spannung erhält man nämlich am Ausgang des Operationsverstärkers keine Spannung. Ich habe hierfür einfach die vom Liion-Akku kommenden Drähte vertauscht angeschlossen.

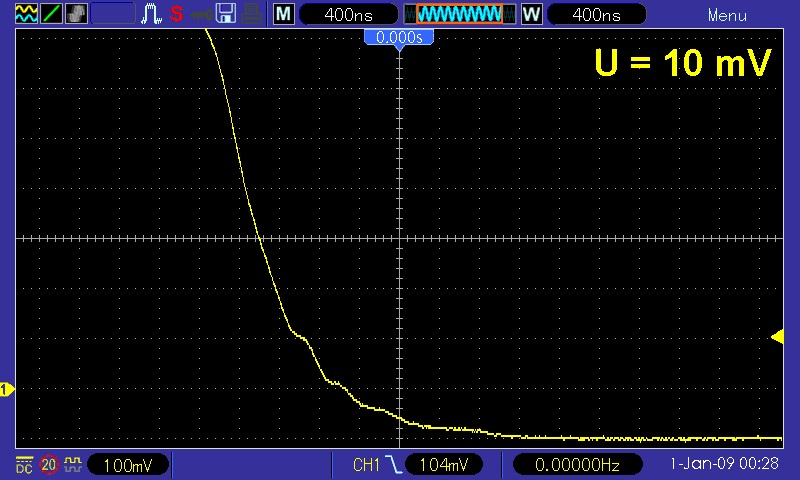
Habe die Schaltung dann auch noch mit den sich trennenden Golddrähten anstelle des Relais getestet. Die Ergebnisse sind ähnlich. Auch hier hin und wieder einige Stufen aber eher zufällig als reproduzierbar.

 

---

 

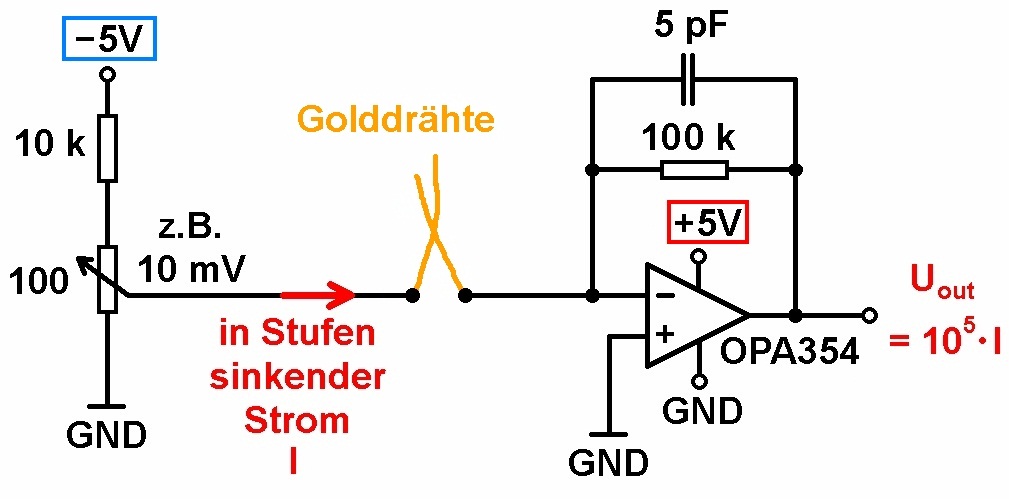
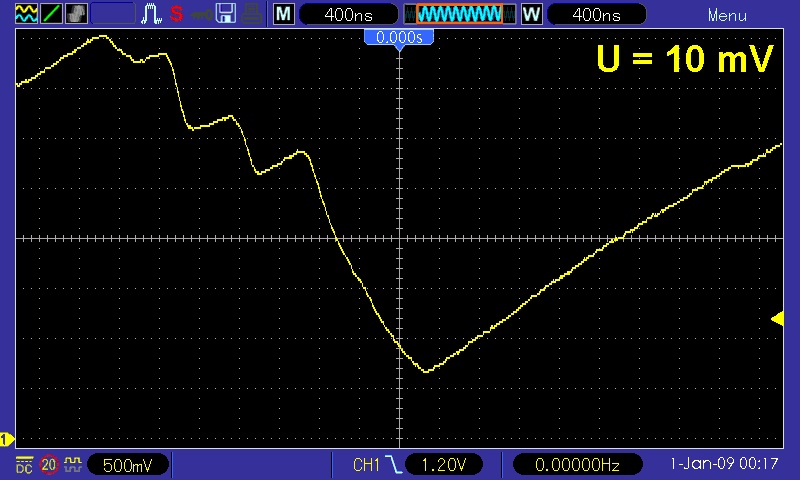
Bei einem zweiten, ähnlichen Versuch verwendet man anstelle des sich öffnenden Relais zwei dünne, sich berührende Golddrähte. Schlägt man mit der Faust auf den Tisch, so bewegen sich die Golddrähte aufgrund der Erschütterung und es kann sein, dass sie sich nicht mehr berühren. Beim Öffnen des Kontakts kommt es wieder zur Ausbildung von Nanoleitern mit dem gequantelten Leitwert.

Bildquelle: PLUS LUCIS 2/97; https://docplayer.org/41378856-Quantisierung-des-leitwerts-in-eindimensionalen-goldkontakten.html

Die Leitwerte G = 1/R sind im Nanodraht quantisiert und zwar mit DG = 1/12.9 kW. Die Leitwerte in den Nanodrähten können also nur die Werte n / 12.9 kW annehmen.

Daher sind bei obiger Schaltung folgende Spannungen am Messwiderstand R_m zu erwarten:

Bildquelle: PLUS LUCIS 2/97; https://docplayer.org/41378856-Quantisierung-des-leitwerts-in-eindimensionalen-goldkontakten.html

Den für den Versuch notwendigen 0.1 mm dünnen Golddraht habe ich auf ebay bestellt:

Zum Aufzeichnen des sprunghaften Spannungsverlaufs benötigt man noch ein digitales Speicheroszilloskop. Meines habe ich mir gebraucht um 200 Euro vor einigen Jahren gekauft:

Die beiden Golddrähte aus China sind eingetroffen. Einmal der 10 cm lange 0.1 mm Draht aus purem Gold und dann der 5 m lange und 0.4 mm dicke goldbeschichtete Draht. Mal schauen, ob es mit ihnen klappt, die Stufen aufzuzeichnen.

Als Spannungsversorgung verwende ich zwei AA-Batterien in Serie. So komme ich auf eine Spannung von 3.124 V. Die beiden Widerstände betragen 9.78 kΩ und ziemlich genau 100 Ω.

Damit müsste ich folgende Spannungsstufen am Oszilloskop erkennen:

Die beiden Drahtstücke trenne ich durch Klopfen auf den Boden, sodass es zu Erschütterungen kommt. Hier nun einige Oszilloskopbilder:

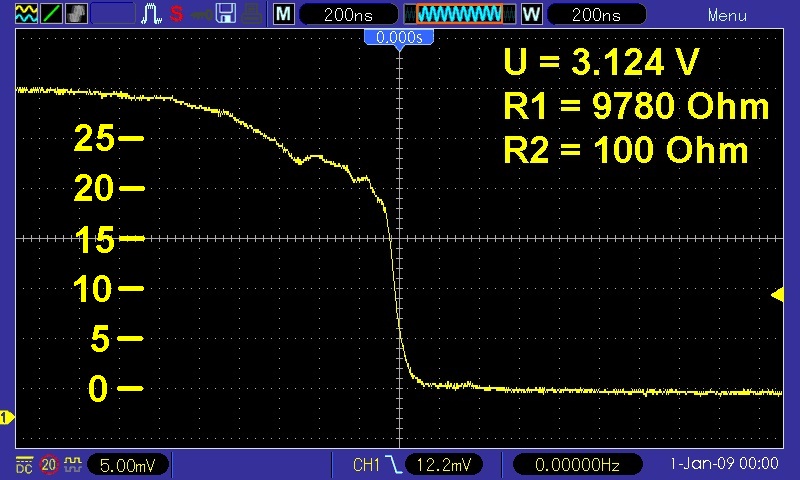
Im Bereich um die 20 mV erhalte ich doch des öfteren einzelne Stufen. Die unterste Stufe (n = 1) bei 13.7 mV habe ich indes leider bisher noch nicht aufzeichnen können. Warum dies so ist, weiß ich im Moment noch nicht. Manchmal erhalte ich eine einzelne Stufe, welche von ca. 14 mV auf 0 mV führt. Aber alle drei ersten Stufen in einer Flanke konnte ich wie gesagt noch nicht verifizieren…

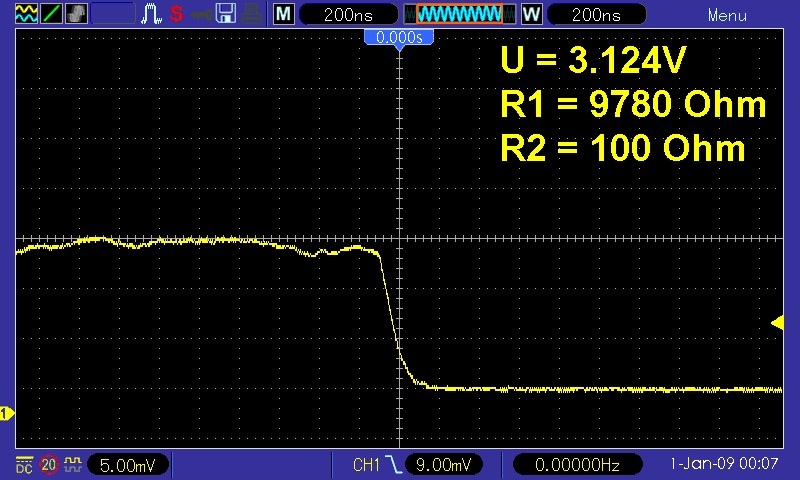
Hier der bisweilen beste erhaltene Spannungsverlauf. Hier sind die beiden untersten Stufen bei 13.7 mV und 19.1 mV zu sehen:

Ich habe die Schaltung noch ein wenig modifiziert. Jetzt messe ich den Strom über den 10 kOhm-Widerstand und verwende nur noch eine einzelne Batterie. Demnach erhalte ich theoretisch folgende Stufen:

Einige erfolgreiche Screenshots:

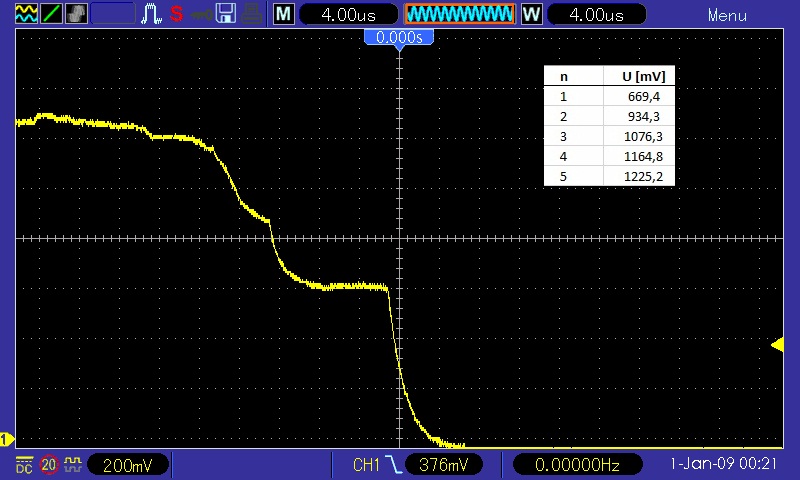
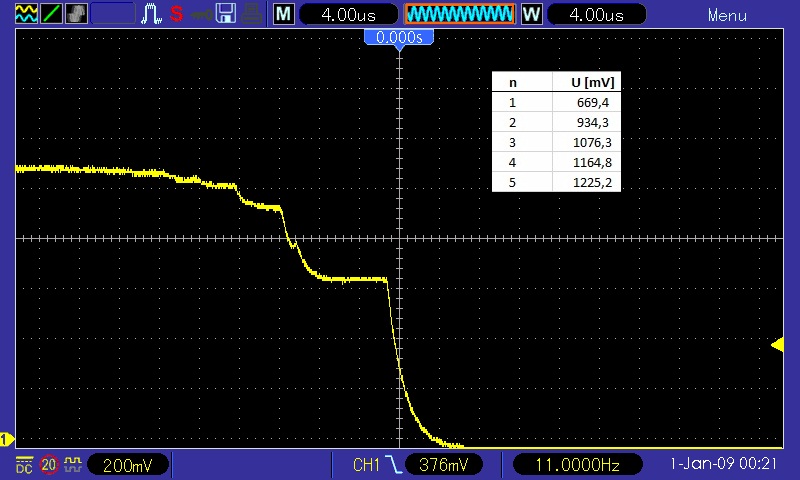
Hier noch das Youtube-Video: