Bei einer Kreisbewegung mit konstanter Bahngeschwindigkeit v handelt es sich um eine beschleunigte Bewegung, da der Geschwindigkeitsvektor seine Richtung ändert. Für die sog. Zentripetalbeschleunigung gilt azp = v²/r = ω² · r und demnach für die Zentripetalkraft Fzp = m · ω² · r. Die Trägheitskraft dazu nennt man Zentrifugalkraft und ihre Formel ist ident.
Hier möchte ich das Experiment „Kugelschwebe“ umsetzen. Dabei handelt es sich um eine kreisrunde Küvette, in deren Hohlraum zwei unterschiedlich schwere Kugeln gegeben werden. Danach versetzt man die Küvette in Rotation.
Bildquelle: www.ntl.de
Meine Kugelschwebe habe ich mir nach eigener Vorgabe 3d-drucken lassen:
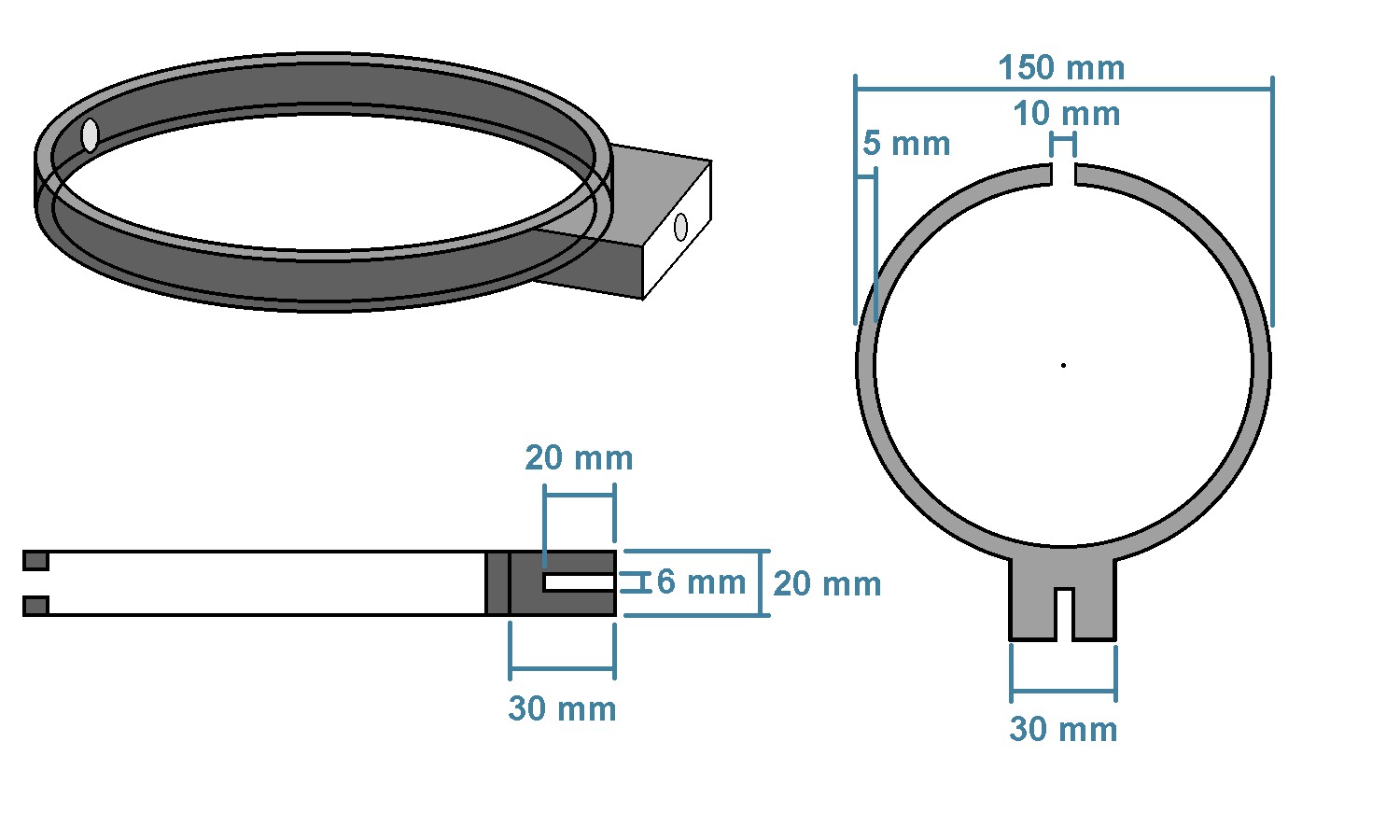
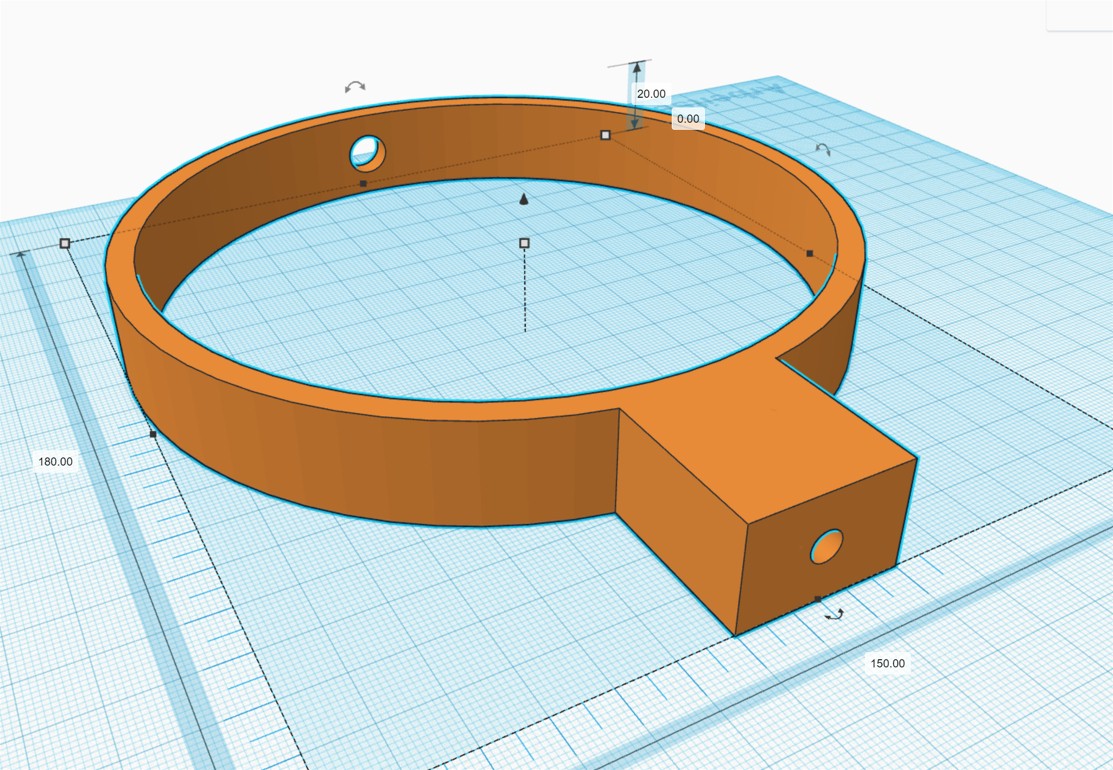


Als Wände verwende ich zwei 150 mm messende, kreisrunde Plexiglasscheiben von Amazon:

Die beiden in der Küvette befindlichen Kugeln steigen bei einer Drehung in die Höhe und es stellt sich ein Winkel α ein. Dieser ist unabhängig von der Masse der Kugel. Daraus schließt man, dass neben der Gewichtskraft Fg = m·g auch die Zentrifugalkraft proportional zur Masse m sein muss.
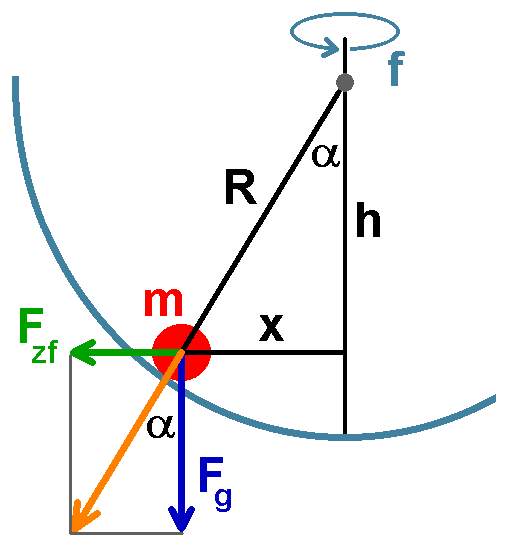
Die Abhängigkeit des Winkels α in Abhängigkeit von der Drehfrequenz f lässt sich wiefolgt herleiten:

Mit zunehmender Drehfrequenz f steigt der Winkel α an und strebt gegen 90°.
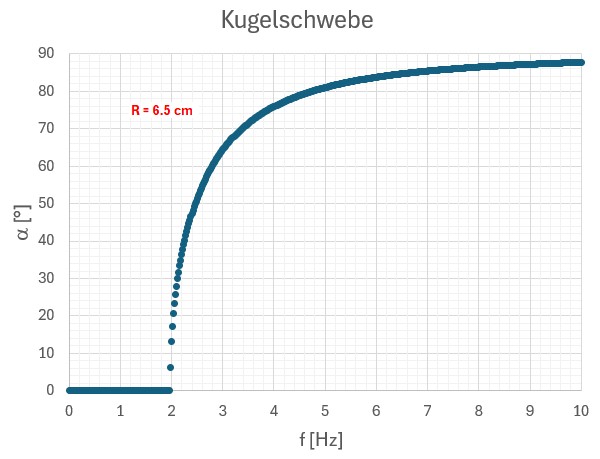
Man erkennt anhand des Graphen aber auch einen kritischen Bereich geringer Drehfrequenz. Dort ist das Argument des arccos(…) größer als 1!
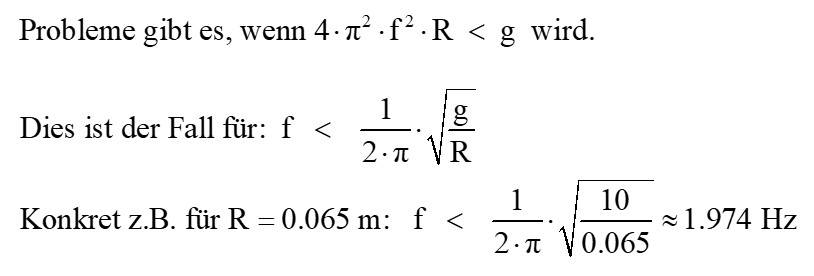
Ich möchte den Winkel α in Abhängigkeit von der Drehfrequenz f experimentell ermitteln. Wenn die Plexiglasscheiben angekommen und eingeklebt sind, geht es hier weiter…
So, die Scheiben sind inzwischen angekommen und bereits verklebt:


Ich verwende zwei 10 mm Kugeln, eine aus Kunststoff und die andere aus Stahl:

In Rotation versetze ich die Kugelschwebe mit meiner Bohrmaschine. Für diese habe ich mir eine Tischhalterung auf Amazon besorgt:




Damit ich die Drehzahl weit genug absenken kann, steuere ich die Bohrmaschine mit meinem Variac an. Die Bohrmaschine setzt sich allerdings erst knapp unter 220V in Gang…

Die Drehzahl bestimme ich wie so oft mit meinem Arduino-Drehzahlmesser auf Basis eines IR-Näherungsmoduls…



Die experimentellen Ergebnisse liegen recht nahe bei den theoretischen Sollwerten:
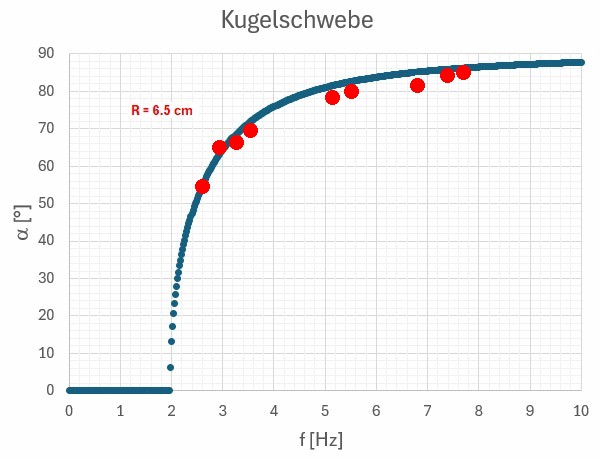
Man kann die Küvette aber nicht nur mit zwei Kugeln füllen, sondern auch mit Wasser. Rotiert man dann die Küvette, so verformt sich der Wasserspiegel aufgrund der Zentrifugalkraft. Aber welcher mathematischen Formel gehorcht dann die Wasseroberfläche?
Die Wasseroberfläche orientiert sich immer normal auf die wirkende Gesamtkraft. Wirkt nur die vertikale Schwerkraft, so richtet sich die Wasseroberfläche horizontal aus. Kommt aber noch die Zentrifugalkraft hinzu, ist dies anders. Hier die kurze Herleitung:
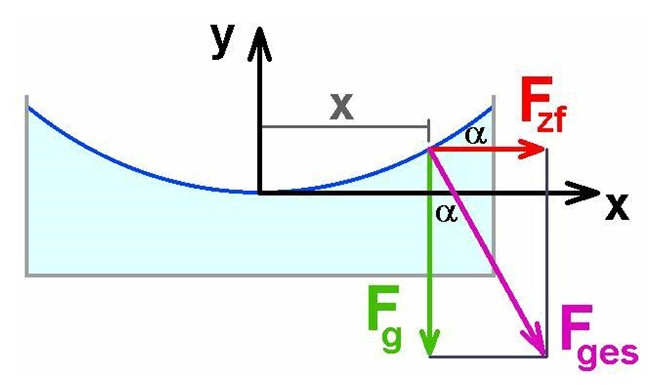

Die Oberfläche gehorcht also einer Parabelfunktion y(x) = a·x². Der Faktor a ist proportional zu f², d.h. die Parabel ist umso steiler, je schneller das Wasser rotiert. Dies ist nachvollziehbar…
Bei diesem Experiment werde ich mit der Software Tracker die Funktion y(x) der Oberfläche bei einer bestimmten Drehfrequenz f bestimmen und mit der Theorie (obige Formel) vergleichen.

Damit man das Wasserparaboloid besser sieht, habe ich es mit Lebensmittelfarbe eingefärbt.

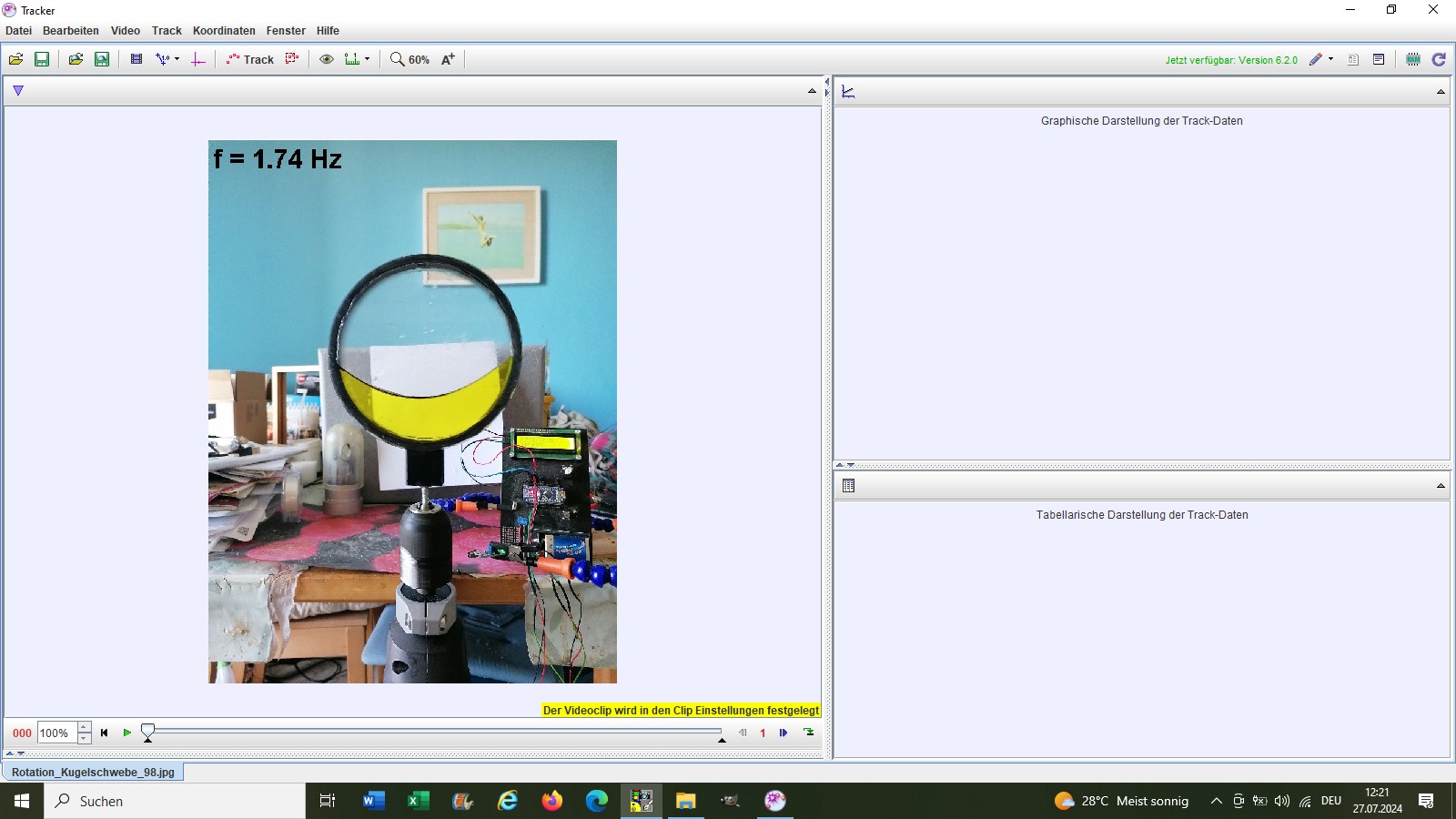
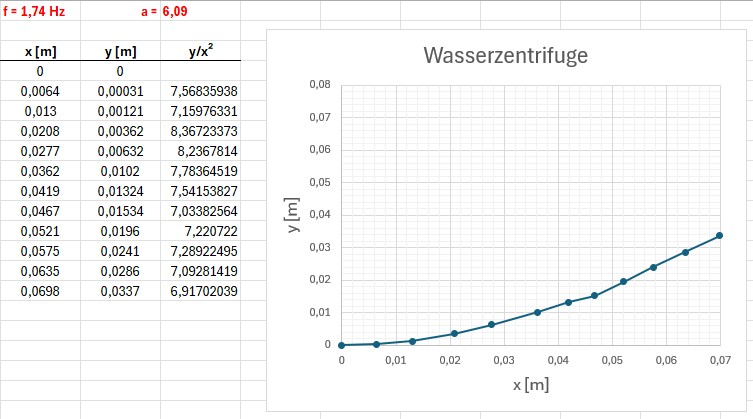
Es gilt ja y(x) = a · x². Dividiert man daher die y-Werte durch x², so sollte sich je nach Drehzahl f ein konstanter Wert a ergeben. Dies habe ich oben in der letzten Spalte überprüft und erhalte experimentell Werte im Bereich von a = 7.4.
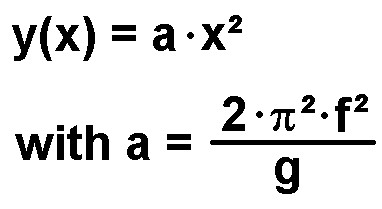
Laut Theorie sollte a für f = 1.74 Hz genau 6.09 betragen…
Für eine höhere Drehzahl (f = 2.98 Hz) habe ich die Parabel auch noch mittels der Software Tracker erfasst:
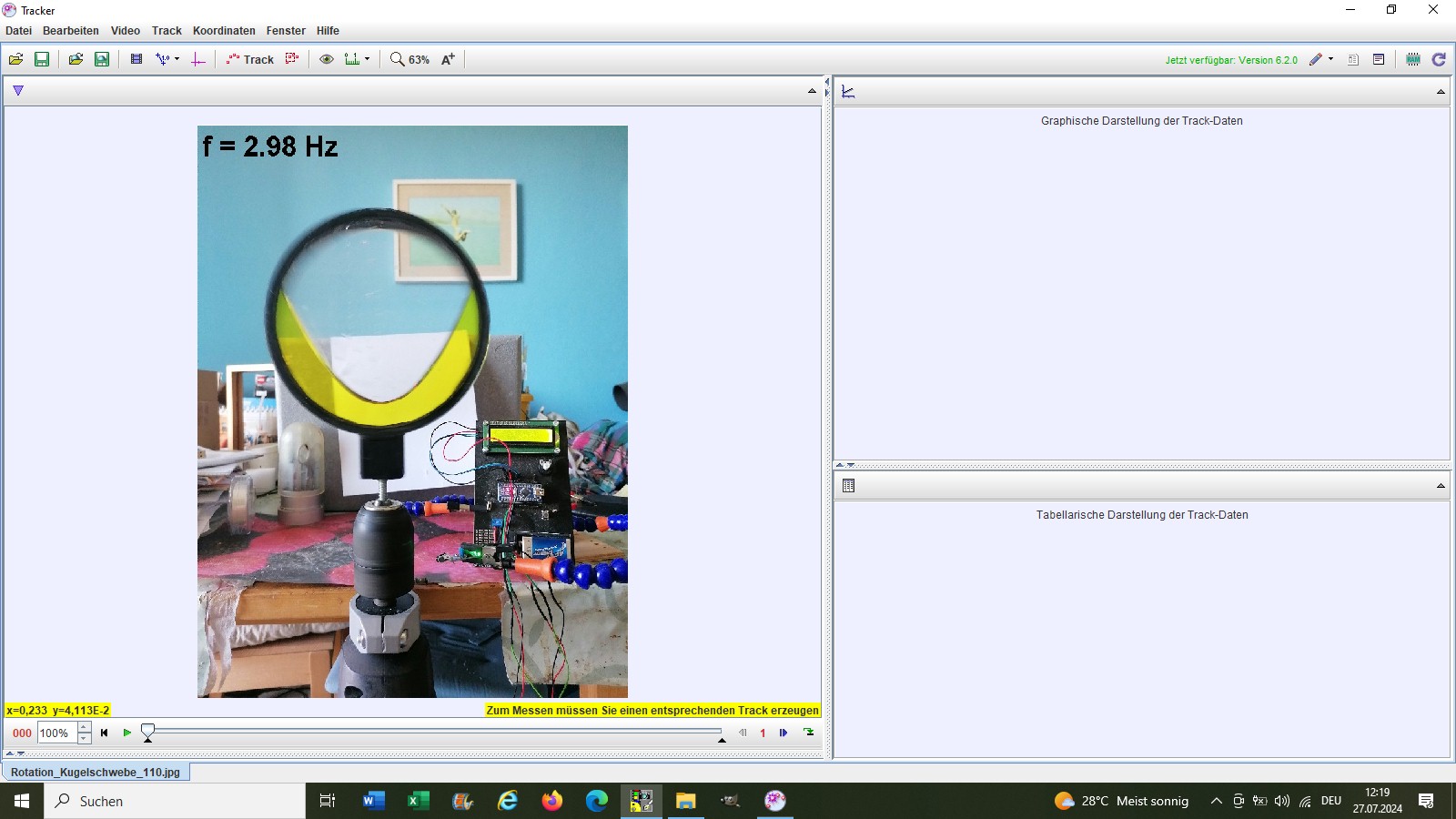
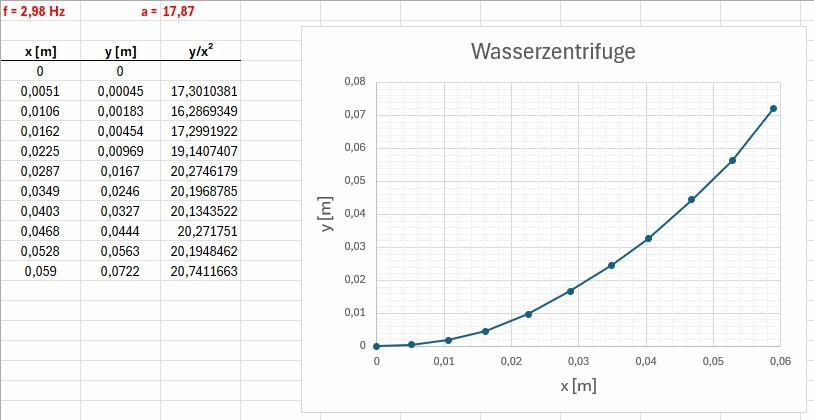
Hier liegen die experimentellen Ergebnisse für den Parameter a im Bereich 16.3 und 20.7 bei einem Sollwert von 17.87. Damit bin ich eigentlich zufrieden 😉
Zum Abschluss noch das Youtube-Video:

