
Dieser nach den Physikern Albert Einstein und Wander Johannes de Haas benannte Effekt zeigt den Zusammenhang zwischen dem magnetischen Moment µ und dem Drehimpuls von Elektronen. Er ist ein makroskopischer Nachweis des Eigendrehimpuls (sog. Spin) der Elektronen und verdeutlicht die Zusammenhänge zwischen makroskopischen Ferromagnetismus und atomaren Gegebenheiten.
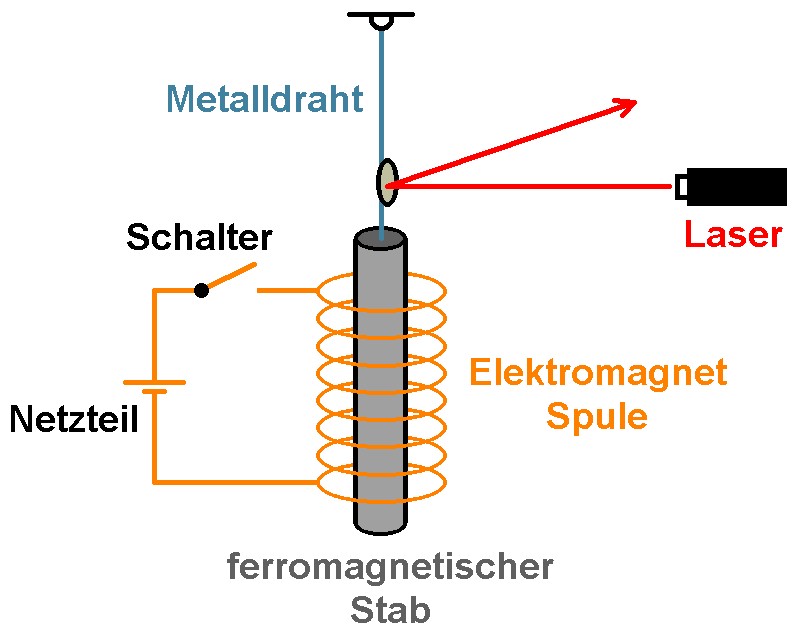
Der experimentelle Aufbau ist eigentlich sehr simpel. Ein ferromagnetischer Stab z.B. aus Eisen befindet sich im Inneren einer Spule, welche über einen Schalter mit einem Netzteil verbunden ist. Der Eisenstab hängt an einem dünnen Metalldraht und kann somit eine Drehbewegung/Schwingung vollführen. Schaltet man das Netzteil ein, so vollführt der Eisenstab eine Schwingung um seine Längsachse. Um diese Schwingung dann auch erfassen zu können, befindet sich am Ende des Stabs ein Spiegel. Dieser wird mit einem Laser anvisiert und der reflektierte Strahl zeigt dann die Rotation des Stabs an.
Warum kommt es aber zu solch einer Schwingung? Beim Versuch zum Zeeman-Effekt (https://stoppi-homemade-physics.de/zeeman-effekt/) bzw. zur Elektronenspinresonanz (https://stoppi-homemade-physics.de/elektronenspinresonanz-esr/) wurde bereits gezeigt, dass ein atomarer Drehimpuls L mit einem magnetischen Moment µ gekoppelt ist. Ausgegangen ist man dabei klassisch von einem Kreisstrom, der ja durch das um das Proton kreisende Elektron hervorgerufen wird. Der Zusammenhang lautet:
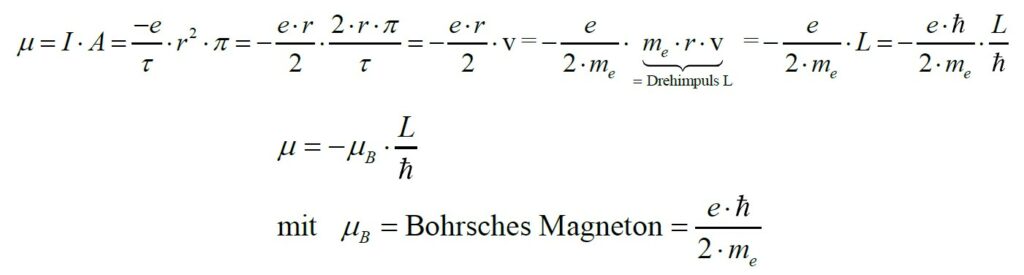 Diese Formel für das magnetische Moment µ muss noch um den sog. Lande-Faktor g ergänzt werden. Für reinen Bahndrehimpuls L beträgt dieser Faktor 1, bei reinen Spin (Eigendrehimpuls) hingegen fast genau 2.
Diese Formel für das magnetische Moment µ muss noch um den sog. Lande-Faktor g ergänzt werden. Für reinen Bahndrehimpuls L beträgt dieser Faktor 1, bei reinen Spin (Eigendrehimpuls) hingegen fast genau 2.
 Mit dem Drehimpuls L, bei dem es sich also um den Bahndrehimpuls oder den Spin des Elektrons handeln kann, ist ein magnetisches Moment in entgegengesetzter Richtung verknüpft. Befindet sich der Eisenstab in keinem äußeren Magnetfeld (B = 0), so sind sämtliche atomaren magnetische Momente und damit einhergehend auch alle Drehimpulsvektoren komplett regellos verteilt. Dadurch heben sie sich makroskopisch betrachtet gegenseitig auf, sprich µges und Lges sind beide 0!
Mit dem Drehimpuls L, bei dem es sich also um den Bahndrehimpuls oder den Spin des Elektrons handeln kann, ist ein magnetisches Moment in entgegengesetzter Richtung verknüpft. Befindet sich der Eisenstab in keinem äußeren Magnetfeld (B = 0), so sind sämtliche atomaren magnetische Momente und damit einhergehend auch alle Drehimpulsvektoren komplett regellos verteilt. Dadurch heben sie sich makroskopisch betrachtet gegenseitig auf, sprich µges und Lges sind beide 0!
Was passiert aber nun, wenn man die Spule mit Stromversorgt und sich dadurch der Eisenstab in einem Magnetfeld befindet (B ≠ 0)? Die magnetischen Momente µ der Elektronen werden sich natürlich ausrichten und zwar in jene Richtung mit der geringsten potentiellen Energie. Dies ist vereinfacht ausgedrückt parallel zum äußeren Magnetfeld [Anmerkung: Eigentlich kann sich das magnetische Moment bzw. der Drehimpuls niemals komplett in Richtung des Magnetfelds ausrichten. Dies hängt damit zusammen, dass die Länge des Drehimpulses √l·(l+1) · (h/2·π) beträgt, dessen z-Komponente allerdings mℓ · (h/2·π)]
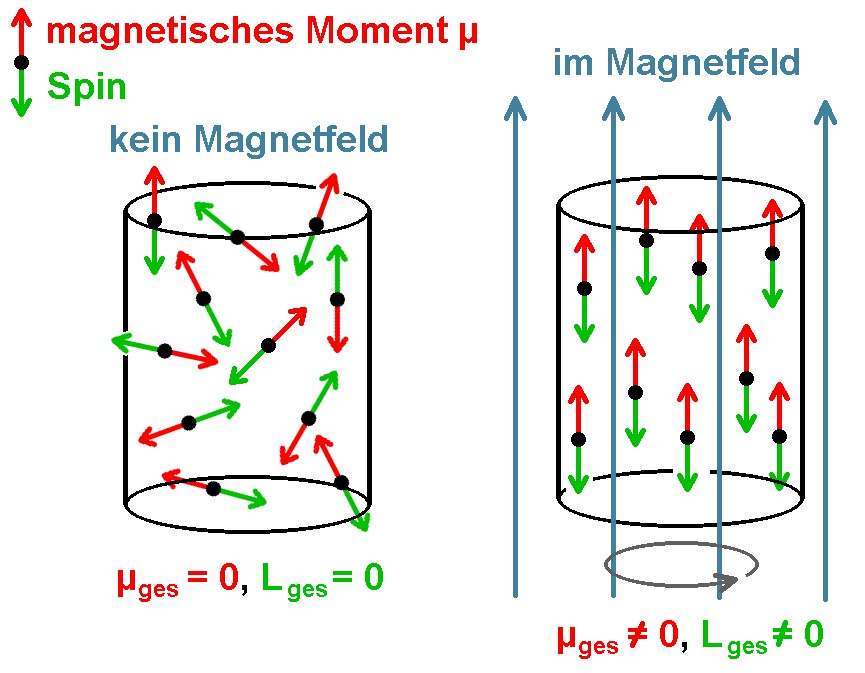
Jetzt wissen wir aber, dass mit dem magnetischen Moment µ ein Drehimpuls L gekoppelt ist. Richten sich die magnetischen Momente aus, so sind auch die atomaren Drehimpulse notgedrungen ausgerichtet. In Summe ergibt sich nun ein makroskopischer Drehimpuls Lges ≠ 0. Aus dem Physikunterricht kennt ja der eine oder andere noch die sog. Erhaltungssätze. Diese besagen, dass unter bestimmten Bedingungen bestimmte physikalische Größen wie die Gesamtenergie E, der Impuls p oder aber auch der Drehimpuls L gleich bleiben.
Zu Beginn des Experiments bei noch offenen Schalter beträgt der Drehimpuls des ruhenden Stabs logischerweise L = 0. Nach Schließen des Schalters muss der Gesamtdrehimpuls aber weiterhin 0 sein. Die ausgerichteten Elektronen sorgen nun aber für einen Drehimpuls ungleich 0. Demzufolge muss sich der Eisenstab quasi in entgegengesetzter Richtung zu drehen beginnen um diesen Drehimpuls wieder auszugleichen. Und genau diese makroskopische Drehung basierend auf dem atomaren Spin der Elektronen beobachtet man beim Einstein de Haas Effekt 😉
Ich werde es einmal mit dieser Spule bestehend aus einer Lage 0.7mm Kupferlackdraht versuchen. Den Eisenstab besorge ich mir beim örtlichen Baumarkt.



Hier einmal die Theorie zum Experiment, welche ich mir selbst überlegt habe:
 Das Richtmoment R des Metalldrahts lässt sich also eibfach aus der Periodendauer τ der Schwingung um die Längsachse ermitteln. Das Trägheitsmoment IStab ist auch bekannt und setzt sich nur aus der Masse m des Stabs und dessen Radius r zusammen. Durch das Einschalten des Stroms durch die Spule klappen die magnetischen Momente und damit zusammenhängend die Drehimpulse der Elektronen um. Infolge erhält der Eisenstab als Ausgleich durch die Erhaltung des Drehimpulses einen Startdrehimpuls L0. Dieser lässt sich wiefolgt experimentell ermitteln:
Das Richtmoment R des Metalldrahts lässt sich also eibfach aus der Periodendauer τ der Schwingung um die Längsachse ermitteln. Das Trägheitsmoment IStab ist auch bekannt und setzt sich nur aus der Masse m des Stabs und dessen Radius r zusammen. Durch das Einschalten des Stroms durch die Spule klappen die magnetischen Momente und damit zusammenhängend die Drehimpulse der Elektronen um. Infolge erhält der Eisenstab als Ausgleich durch die Erhaltung des Drehimpulses einen Startdrehimpuls L0. Dieser lässt sich wiefolgt experimentell ermitteln:

φ0 ist dabei die Winkelamplitude der angeregten Schwingung um die Längsachse des Eisenstabs. Diesen Winkel berechnet man einfach aus dem wandernden Auftreffpunkt des Laserstrahls.

Um den Landefaktor g ausrechnen zu können, müssen wir das gesamte magnetische Moment μges aller Elektronenspins zusammen und das Drehmoment Lges = L0 aller Elektronen zusammen kennen.

Letzteres ist wie schon gezeigt experimentell über die Amplitude der Winkelauslenkung bestimmbar. Wie aber nun das makroskopische magnetische Moment μges praktisch bestimmbar ist, ist mir im Moment noch nicht klar. Es einfach mit nElektronen· μBohr anzusetzen ist natürlich nicht erlaubt 😉 Es muss daher eine andere Lösung geben, wie diese Größe experimentell bestimmt werden kann. Wenn es Neuigkeiten gibt, geht es hier weiter…
Hier gibt es eine ausgezeichnete Projektarbeit zum Einstein de Haas Versuch:
https://ap.physik.uni-konstanz.de/projektpraktikum/PP2012/Bericht-Einstein-de-Haas.pdf
Wie ich es mir schon dachte, ist die Ermittlung des Landefaktors mit diesem Experiment nicht ganz so trivial. Bevor ich aber diesen Weg einschlage (es geht mir eben nicht nur um den Einstein de Haas Effekt an sich sondern auch um die Berechnung des Landefaktors), habe ich mir aber meine eigenen Gedanken gemacht und die angefügte Herleitung erstellt.
Wie ich das Richtmoment R aus den unerzwungenen Schwingungen des Torsionspendels und den Startdrehimpuls L0 des Eisenstabs ermittle, ist oben angeführt. Danach geht es so weiter:



Darin sind eigentlich alles experimentell ermittelbare Größen, angefangen vom Richtmoment R des Torsionsfadens, über den Auslenkwinkel φ0 nach Einschalten des Spulenstroms bis hin zu den Induktivitäten Lmit/ohne Kern der Spule mit bzw. ohne Eisenkern zur Bestimmung der Permeabilität µr.
Als Eisenstab eignet sich Weicheisen am besten. Daher habe ich einen solchen beim Schulmittelbedarf bestellt:

Der Grund warum sich Weicheisen besser eignet als hartmagnetisches Material wird anhand der nachfolgenden Bilder deutlich:



Hartmagnetische Materialien besitzen eine hohe Remanenz, sprich eine große verbleibende Magnetisierung nach Ausschalten des äußeren Magnetfelds. Dadurch ist die Hysteresekurve viel breiter und es liegt verglichen mit der viel schmäleren Hysteresekurve beim weichmagnetischen Stoff ein deutlich weniger lineares/direkt proportionales Verhalten zwischen Magnetisierung M und Außenfeld H vor. Aber genau so einen linearen Zusammenhang benötigt man für das Experiment und von diesem wurde auch in der obigen Herleitung ausgegangen mit M = (µr – 1) · H.
Wichtig ist auch noch, dass man sich bei der Magnetisierung durch das äußere Magnetfeld nicht schon im Sättigungsbereich des Eisenstabs befindet, sondern noch im linearen Anfangsanstieg! Denn wenn bereits alle magnetischen Momente durch das Außenfeld ausgerichtet sind, gilt natürlich auch kein direkt proportionaler Zusammenhang mehr zwischen M und H, denn dann bleibt ja die Magnetisierung auf ihrem maximalen Wert stehen und wächst nicht mehr!
Anders als bei den im Internet geschilderten Versuchsdurchführungen mit angelegter Wechselspannung an die Erregerspule werde ich es ja nur mit einem einzelnen Startimpuls versuchen, sprich die Spule einmalig einschalten und dann eingeschalten lassen. Dadurch klappen die magnetischen Momenge nur einmalig zu Beginn um und durch die Drehimpulserhaltung erhält der Eisenstab auch nur einmalig zu Beginn einen Drehimpuls.
In die Berechnung des Landefaktors fließt ja die Startamplitude φ0 ein. Da mein Resonator aber sicherlich nicht ungedämpft ist, messe ich natürlich eine zu geringe Amplitude. Die theoretische Herleitung mit T = –R·φ ging aber vom ungedämpften Fall aus. Um die ungedämpfte Amplitude abschätzen zu können, werde ich zunächst den Amplitudenverlauf der gedämpften Schwingung aufzeichnen. Aus dem Dämpfungsfaktor Amplitude(n+1)/Amplitude(n) werde ich dann die theoretisch ungedämpfte Amplitude berechnen.


Hierfür habe ich mir eine EXCEL-Simulation zur erzwungenen Schwingung mit/ohne Dämpfung geschrieben. Den einmaligen Startdrehimpuls simuliere ich einfach mit einer Startgeschwindigkeit ≠ 0. Die Erregerkraft ist 0 und spielt im Verlauf der Simulation also keine Rolle mehr. Ich werde die Dämpfung/Reibung in der Simulation so verändern, bis sich die simulierte Amplitudenabnahme mit der realen deckt. Danach gehe ich mit der Dämpfung auf 0 und schaue, um welchen Faktor sich die ungedämpfte Amplitude von der ersten (gedämpften) Amplitude unterscheidet. Diesen Faktor werde ich dann auf die experimentell ermittelte Winkelamplitude φ0 übertragen.
Beispiel: Angenommen die Amplituden nehmen um den Faktor 0.85 jeweils ab. Dann verändere ich in der Simulation die Dämpfung so lange, bis die Amplituden dort ebenfalls um den Faktor 0.85 abnehmen. Die erste Startamplitude beträgt dann zum Beispiel 2.5. Jetzt setze ich die Reibung auf 0 und simuliere nochmals. Nun ist die Startamplitude z.B. auf 3 gewachsen. Der Vergrößerungsfaktor beträgt somit 3/2.5 = 1.2. Die experimentell gemessene erste Winkelamplitude φ0 soll zum Beispiel 5.6° sein. Die ungedämpfte erste Winkelamplitude würde demnach 5.6° · 1.2 betragen. Diesen Wert setze ich dann in die Formel zur Berechnung des Landefaktors ein. Mal schauen, ob das alles auch so klappt wie ich es mir gedacht habe 😉
Bei meiner Methode zur Berechnung des Landefaktors wird die Permeabilität μr des Eisenstabs benötigt. Diese kann man über die Induktivität L einer Spule ohne Kern bzw. mit diesem Kern berechnen. Das Verhältnis Lmit Kern / Lohne Kern sollte dann genau der Permeabilität entsprechen. Da der Weicheisenstab noch nicht eingetroffen ist, startete ich einmal eine Messung mit einem Inbusschlüssel als Kern. Ich verfüge im Moment über 2 LC-Meter. Der einfache Komponententester zeigte leider die Induktivität ohne Kern überhaupt nicht an.

Mit dem Multimeter erhielt ich zwar Werte für die Induktivität, jedoch beträgt der kleinste Messbereich immerhin bereits 2 mH und somit der kleinste angezeigte Wert 1 µH.


Laut diesen Messwerten beträgt die Permeabilität des Inbusschlüssels μr = 35/1 = 35, was aber doch deutlich zu klein sein sollte. Deshalb habe ich mir ein günstiges LC-Meter auf aliexpress bestellt. Mal schauen, ob ich mit diesem vernünftige Werte erhalte.

Ich werde die Induktivität aber auch noch mittels folgender Schaltung messen/überprüfen:
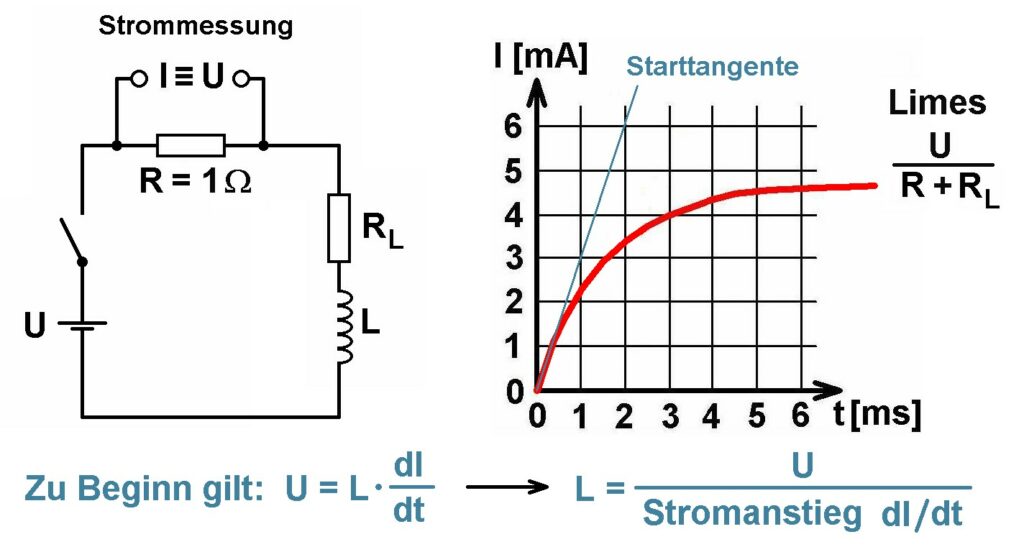
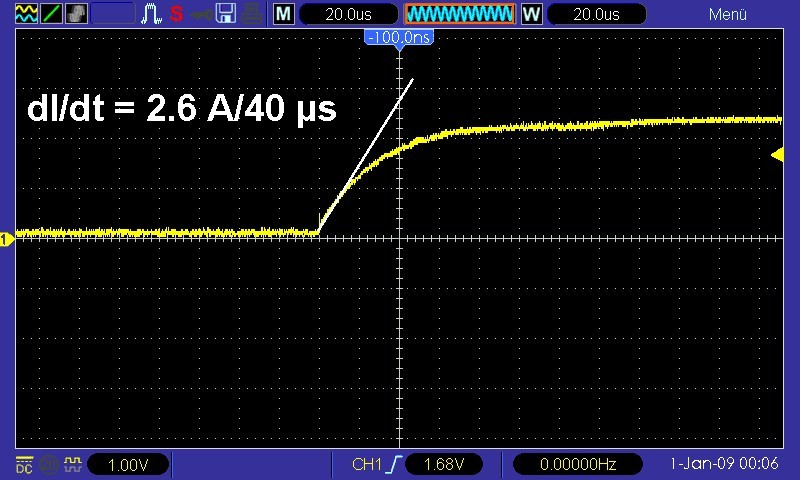
Man schließt die zu messende Induktivität (Induktivität L, Widerstand RL) in Serie mit dem Strommesswiderstand R = 1 Ω über einen Schalter an eine Gleichspannung U. Schließt man den Schalter, so steigt der Strom zunächst steil an. Aus dem Stromanstieg dI/dt lässt sich dann einfach die Induktivität der Spule berechnen. Im obigen Graphen wäre dieser Stromanstieg konkret dI/dt = 3 mA/1 ms = 3 A/s. Diese Messung führe ich einmal mit der Induktivität ohne Kern und einmal mit Kern durch und berechne daraus wieder die Permeabilität μr. Wenn ich mit diesen zwei Methoden stark unterschiedliche Werte erhalte, muss ich mir etwas einfallen lassen.
Heute habe ich die Induktivität einer Luftspule mittels obiger Formel für den Stromanstieg dI/dt experimentell bestimmt. Ich komme auf eine Induktivität von 76.9 µH.



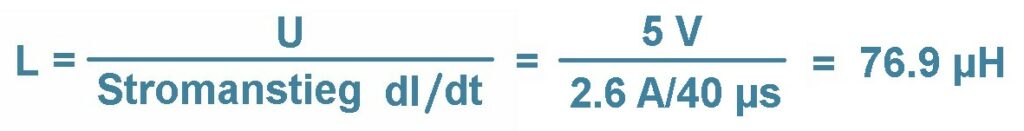
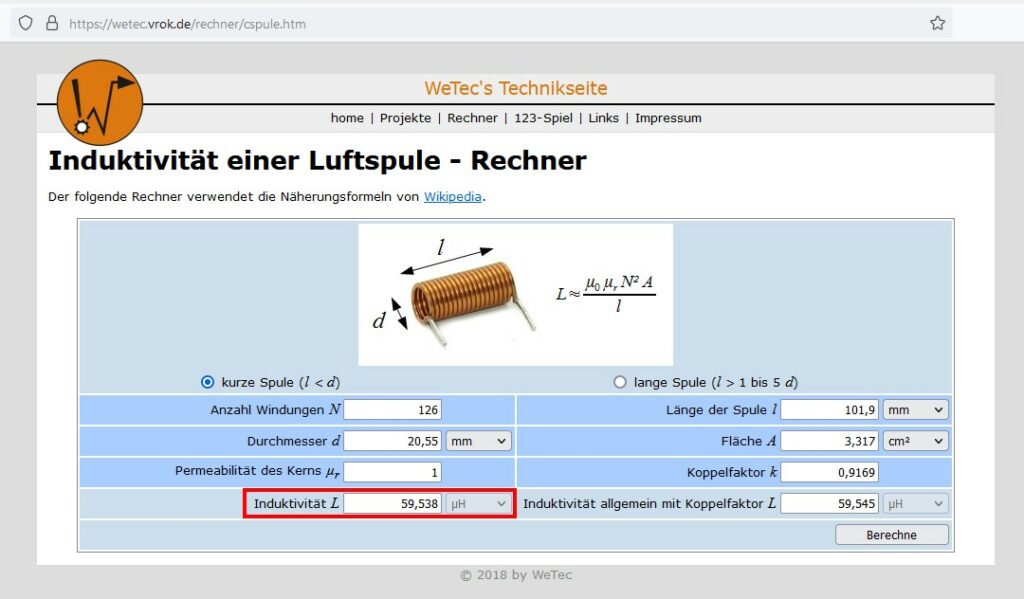
Zum Vergleich habe ich auch einen online-Rechner für die Induktivität bemüht. Damit erhalte ich einen theoretischen Wert von rund 60 µH. Eine etwas bessere Übereinstimmung hätte ich mir ehrlich gesagt schon gewünscht, aber so weit liegen die beiden Werte nun auch wieder nicht auseinander…
Weil ich neugierig war, habe ich nun die Induktivität der Spule auf eine zweite experimentelle Art bestimmt und zwar durch Auswertung der Frequenz f eines Schwingkreises:


Zuerst testete ich den Aufbau mittels einer Spule bekannter Induktivität (L = 1 mH) in Kombination mit einem 220 nF Kondensator:



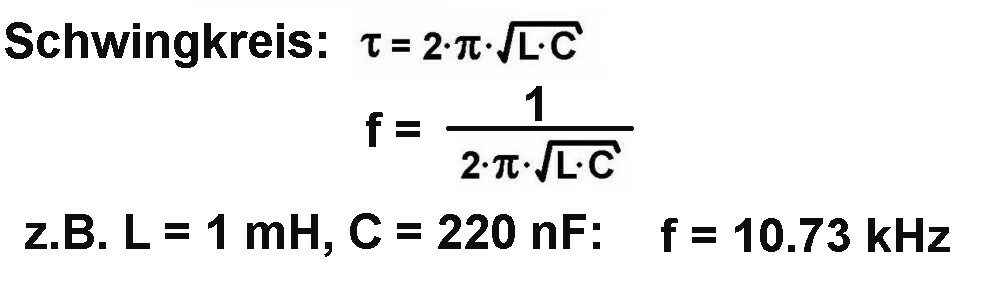
Die gemessene Frequenz des Schwingkreises betrug rund 10.5 kHz, der Sollwert beträgt 10.73 kHz. Dann habe ich die Luftspule unbekannter Induktivität angeschlossen. Die Frequenz des Schwingkreises betrug ca. 44.15 kHz:



Mit dieser Frequenz von 44.15 kHz berechnete ich dann die Induktivität und erhielt L = 59.1 µH. Dies liegt extrem nahe dem theoretischen Wert von L = 59.5 µH 🙂

Ich werde daher zur Bestimmung der Permeabilität des Weicheisenstabs ganz klar auf die zweite experimentelle Methode mit dem Schwingkreis zurückgreifen.
Für die Spule zur Bestimmung der Permeabilität des Weicheisens bzw. für die Spule des Einstein-de Haas Versuchs verwende ich 0.6 mm Kupferlackdraht. Diesen habe ich mit meinem Milliohmmeter (https://stoppi-homemade-physics.de/milliohmmeter/) vermessen und komme auf einen Widerstand von 58 mΩ/m. Dies deckt sich sehr gut mit Tabellenwerten. Durch Bestimmung des Spulenwiderstands kann ich nun sehr einfach auf die Windungszahl n zurückrechnen, die ich ja für die Berechnung des Landefaktors benötige (siehe Formel oben).



Die gute Nachricht: Der Weicheisenstab ist angekommen.



Die schlechte: Die Bestimmung seiner relativen Permeabilität μr erweist sich als ungleich komplizierter als gedacht/erhofft.
In 100ten Internetquellen bzw. Büchern werden zur Berechnung der Induktivität einer Zylinderspule Abbildungen/Formeln wie diese veröffentlicht:

Bildquelle: https://studyflix.de/elektrotechnik/induktivitat-und-spule-1542
Hier gibt es auch einen online-Rechner zu dieser Aufgabe: https://wetec.vrok.de/rechner/cspule.htm
Diese Formel suggeriert, die Permeabilität μr zum Beispiel einfach durch Division Lmit Kern / Lohne Kern ausrechnen zu können. Genau dies habe ich gemacht/probiert, und musste feststellen, dass meine Ergebnisse extrem stark von den Tabellenwerten für Weicheisen abweichen. Die relative Permeabilität μr von Weicheisen sollte im Bereich um die 1000 und höher liegen. Mit einem Kern dieser Permeabilität sollte die Induktivität auch um den Faktor 1000 gegenüber der Luftspule wachsen und das tut sie auch laut dieser Rechner.
Meine höchsten erhaltenen Werte liegen im Bereich um die 30. Die relative Permeabilität habe ich auf 3 unterschiedliche experimentelle Arten versucht herauszufinden und zwar durch Messung der Induktivität L bzw. durch Messung der Flussdichte B.
a.) Messung der Induktivität L über den Stromanstieg dI/dt
Legt man eine Gleichspannung U über einen Widerstand R an eine Spule (Induktivität L, Spulenwiderstand RL) sprunghaft an, so steigt der Strom nur allmählich. Grund dafür ist die bremsende Wirkung der Induktivität/Spule. Ganz zu Beginn liegt die gesamte Spannung U noch an der Induktivität L an, d.h. es gilt: U = L · dI/dt. Demnach ergibt sich für L = U / (dI/dt). Kennt man U und den Stromanstieg, so kann man sehr einfach die Induktivität ausrechnen.







Anhand der Oszilloskopbilder lässt sich der unterschiedliche Stromanstieg mit/ohne Kern ausrechnen. Die Anstiege differieren etwa um den Faktor 20. Demnach sollte die relative Permeabilität μr des Kerns 20 betragen, was aber für Weicheisen viel zu gering ist. Wie schon erwähnt sollte μr,Weicheisen > 1000 sein!
b.) Messung der Induktivität L über die Frequenz eines Schwingkreises
Die Verhältnisse beim elektrischen Schwingkreis, welcher aus einer Kapazität C, einer Induktivität L und einem ohmschen Widerstand R gebildet wird, scheinen sehr einfach zu sein. Die Frequenz der Schwingung ergibt sich bei nicht zu großer Dämpfung zu: f = 1 / (2 ·π · √(L · C)).


Misst man also die Schwingkreisfrequenz f, so kann man bei bekannter Kapazität C auf die Induktivität L zurückrechnen. Genau das habe ich experimentell auch gemacht.





Mit Kern müsste eigentlich die Induktivität L und damit auch die Periodendauer τ der Schwingung stark anwachsen, was sie aber nicht tut. Sie wird nur zunehmend gedämpfter. Grund dafür sind zum einen einmal die großen Wirbelströme (im Gegensatz zu Ferrit besitzt ja Weicheisen einen extrem niedrigen Widerstand, was Wirbelströme natürlich begünstigt) und zum anderen die Geometrie meines Kerns. Ein Stab besitzt notgedrungen eine sehr lange Luftstrecke, welche die Induktivität massiv beeinflusst bzw. senkt. Dies macht dann den Permeabilitätszuwachs durch das Eisen scheinbar völlig zunichte. Mittels der Schwingkreisfrequenz erhalte ich also durch die nahezu unveränderte Frequenz (siehe Oszibilder) keine nennenswerte Steigerung der Induktivität mit Kern und daher auch nur eine sehr niedrige relative Permeabilität μr.
Die Formel für die Induktivität einer Zylinderspule mit Kern scheint also nur dann gültig zu sein, wenn es sich um einen geschlossenen Kern handelt und nicht um einen Stab wie bei mir. Denn laut simpler Formel für L müsste bei Verwendung eines Kerns mit μr = 1000 die Induktivität auf das 1000-fache ansteigen und im Falle des Schwingkreises dessen Frequenz um auf 1/1000-stel sinken, was sie aber absolut nicht tut.
c.) Messung der Induktivität mittel LCR-Meter
Auch mit einem LCR-Meter habe ich die Induktivitäten mit/ohne Kern bestimmt.


Laut dieser Messwerte würde ich fälschlicherweise eine relative Permeabilität von μr = 68 / 5 ≈ 13 herleiten.
d.) Messung der Flussdichte
Der Zusammenhang zwischen der Flussdichte B und der magnetischen Feldstärke H lautet: B = μr · μ0 · H.
Für die Feldstärke H in einer langen Spule gilt zudem: H = n · I / ℓ mit Anzahl der Windungen n, der Stromstärke I und der Spulenlänge ℓ.
Daher gilt für B einer langen Zylinderspule: B = μr · μ0 · n · I / ℓ.
Auch hier dachte ich wieder, die relative Permeabilität einfach mittels Quotienten μr = Bmit Kern / Bohne Kern ausrechnen zu können.
Meine Messergebnisse zeigten aber leider wieder etwas anderes. Ich bestimmte die Flussdichte B mit und ohne Kern am Spulenende bzw. in der Spulenmitte:







Wie man anhand der Messergebnisse sieht, nahm die Flussdichte mit Kern nur etwa um den Faktor 20-30 zu. Daher beträgt mit meiner Herangehensweise die relative Permeabilität des Weicheisenkerns ebenfalls nur 20-30. Eine kurze Überprüfung mittels halbexperimenteller Formel lieferte ein Ergebnis für μr ebenfalls in diesem Bereich:
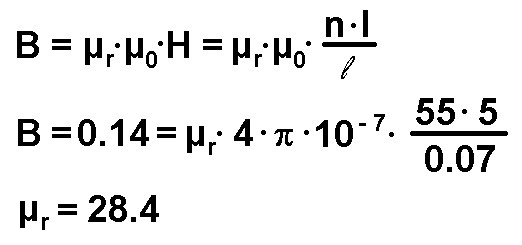
Für die Flussdichte B gilt also dasselbe wie für die Induktivität L: Mit meiner Anordnung lässt sich aus den Messergebnissen leider nicht auf die relative Permeabilität des Weicheisens zurückrechnen.
e.) Messung des Induktionsspannungsstoßes
Die magnetische Flussdichte B lässt sich auch noch auf eine andere Methode ermitteln. Und zwar wickelt man zusätzlich zur Hauptwicklung noch eine weitere Sekundärwicklung mit n = 1 auf den Kern. Die Hauptwicklung schließt man über einen Schalter an eine Gleichspannungsquelle an. Schließt man nun den Schalter, so baut sich das Magnetfeld auf. Durch diese Änderung des magnetischen Flusses kommt es aber in der Sekundärwicklung zu einer Induktionsspannung. Integriert man diese über die Zeit t auf, so erhält man ebenfalls die sich am Ende einstellende Flussdichte B. Mittels dieser kann man dann auch die relative Permeabilität μr bestimmen.
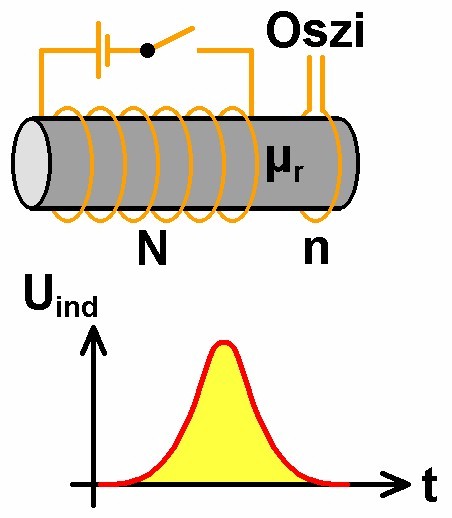



Mit dieser Methode konnte ich die relative Permeabilität zu 34.2 ermitteln. Dies deckt sich eigentlich sehr gut mit den anderen experimentellen Ergebnissen für μr, wenngleich alle Werte sehr viel kleiner sind als der für Eisen angegebene Wert.
Wenn ich keine brauchbare experimentelle Methode zur Bestimmung von μr finde, muss ich wohl notgedrungen auf einen Tabellenwert für die relative Permeabilität von Weicheisen (z.B. 1000) zurückgreifen.
Das Problem ist aber folgendes: Nutze ich anstelle des Stabs etwa einen geschlossenen Ring, so spielt die Luftstrecke keine Rolle mehr und die gemessene Induktivität müsste merklich ansteigen. Das Problem mit den Wirbelströmen hätte ich dann aber nach wie vor, was mir wiederum die gemessene Induktivität stark beeinflusst. Würde ich auf die Magnetfeldmessung setzen, so könnte ich bei einem geschlossenen Ring natürlich nirgends die Hallsonde ansetzen. Um mit dieser die Flussdichte B messen zu können, müsste ich erst recht wieder den Ringkern öffnen und ich hätte wieder die gleichen Probleme wie mit meinem Stab. Wie man sieht, ist alles viel, viel komplizierter, wenn man sich näher mit den physikalischen Dingen beschäftigt.
Ich finde es aber wirklich schlimm, dass in 100ten von Internetlinks und Büchern in keinster Weise auf diese Problematik bei einer Zylinderspule hingewiesen wird. Da wird lediglich von der Spulenlänge ℓ, der Querschnittsfläche A, der Windungszahl n und der Permeabilität des Kernmaterials gesprochen und die Formel L = μr · μ0 · n² · A / ℓ angegeben. Dass etwa das Kernmaterial vollständig geschlossen sein muss bzw. Wirbelströme das Ergebnis auch massiv beeinflussen, wird vollends verschwiegen. Dies war auch der Grund, weshalb ich viel zu naiv an die Sache zur Berechnung von μr herangegangen bin 🙁
Was ich aber in der Zwischenzeit experimentell ermitteln konnte, war das Richtmoment R der verwendeten Nylonschnur mit 0.3 mm Durchmesser. Die Schnur wird mittels zweier M3-Madenschrauben am Weicheisenstab fixiert.





Die gemessene Periodendauer τ einer Schwingung betrug rund 5.5 Sekunden. Damit und mit dem Trägheitsmoment I eines Stabes konnte ich das Richtmoment R zu 1 · 10^ –6 N·m/rad bestimmen:




Auf der Suche nach einer Formel, welche die experimentell bestimmte niedrige Permeabilität mit der tatsächlichen viel höheren Permeabilität des Materials in Beziehung setzt, bin ich auf die effektive Permeabilität μeff gestoßen. Dabei scheint es sich, soweit ich das verstanden habe, eben um die effektiv gemessene Permeabilität handelt. Es gibt auch Formeln, welche μr mit μr verknüpfen. Eine davon sieht so aus:


Für einen Kern mit kleinen Luftspalt scheint dieser Faktor k dem Verhältnis ℓLuft / ℓKern zu entsprechen. In der nachfolgenden Grafik sieht man sehr schön, wie die Steigung der B(H)-Kurve mit zunehmenden Luftspalt immer geringer wird. Die Steigung ist ja ein Maß für die effektive Permeabilität, welche eben bei zunehmenden Luftspalt immer geringer wird.

Diese Formel mit k = ℓLuft / ℓKern gilt allerdings nur bei einem kleinen Luftspalt. Setzt man nämlich ℓLuft = ℓKern, also k = 1, so erhält man sogar eine effektive Permeabilität μeff von knapp unter 1 (siehe online-Rechner unten), was eigentlich einem diamagnetischen Fall entsprechen würde.

Die Größe k wird auch als Demagnetisierungsfaktor bezeichnet. Für diese Größe gibt es etwa für eine Zylindergeometrie Tabellen, wo man je nach Länge/Durchmesser-Verhältnis des Zylinders und der Suszeptibilität χ = μr – 1 den Demagnetisierungsfaktor ablesen kann:


Links:
https://mriquestions.com/uploads/3/4/5/7/34572113/sato_demagnetizing_factors.pdf
https://pdfs.semanticscholar.org/0ab1/b4006e7272f63d880b2d1a168435db6be97d.pdf

Für ein Längen-zu-Durchmesser-Verhältnis des Zylinders von 10 und einer Suszeptibilität von 1000 (was einem μr =1001 entsprechen würde) liegen die Werte für den Demagnetisierungsfaktor im Bereich von 0.015-0.02.
Setzt man diesen Wert in die obige Formel zur Berechnung von μr aus μeff ein, erhält man folgenden Graphen:

Wie man anhand des Graphen sehen kann, beträgt μr ein Vielfaches von μeff. Genau das war ja meine Hoffnung: Für eine bestimmte Geometrie des Kerns (z.B. Zylinder) eine Formel finden, mit welcher ich aus der gemessenen, effektiven Permeabilität μeff auf die “echte” Permeabilität μr des Materials zurückrechnen kann. Mir ist nur der Verlauf des Graphen suspekt: Wenn nämlich der Nenner 1 – k · μeff Null wird, divergiert μr. Für k = 0.0172 beträgt der kritische Wert μeff = 58.1. Mir leuchtet nicht ein, warum ich nicht experimentell eine effektive Permeabilität μeff ≥ 58.1 messen sollte. Aber für diese Werte divergiert μr entweder oder ist negativ.
Ich habe mich jetzt noch einmal mit dem Fall Eisenkern mit kleinem Luftspalt gespielt und eine Formel für μeff hergeleitet. Ausgangsbasis waren die konkreten Berechnungen im folgenden youtube-Video: https://www.youtube.com/watch?v=R1oQFfstFlQ
Nach einer Verallgemeinerung und der Einführung einer effektiven Permeabilität μeff, damit quasi die “alten” einfachen Formeln wieder gelten, erhielt ich folgendes:

Dies ist genau die oben für kleine Luftspalte angegebene Formel 🙂
Sehen wir uns gleich ein konkretes Beispiel mit ℓKern = 12 cm, ℓLuft = 0.5 mm, µr = 1000 an. Man erhält trotz des geringen Luftspalts eine effektive Permeabilität von nur noch 194, also weniger als 1/5 vom tatsächlichen µr des Kernmaterials. Dies erklärt auch, warum ich bei meinem Stab mit seinem viel, viel größeren Luftspalt effektive Permeabilitäten um die 30 messe.
Jetzt habe ich mir gedacht, um die ganzen Probleme mit der Stabgeometrie zu umgehen, baue ich mir mit den Weicheisenstab einen geschlossenen Kern. Nur dann habe ich folgendes Problem: Den bekomme ich mit Sicherheit nicht spaltfrei. Und wie man gesehen hat, bewirken selbst geringste Luftspalte eine dramatische Reduzierung von µeff. Damit µeff = µr ist, müssen die Luftspalte aber defacto 0 sein. Und wenn sie es nicht sind und ich zum Beispiel ein µeff von 200 erhalte, kann ich dann erst recht nicht auf µr hochrechnen, da ich die genauen Maße der Luftspalte nicht kenne. Also hilft mir der geschlossene Kern wohl auch nicht wirklich…
Ich werde bald einen Schlussstrich unter die ganze Sache mit der relativen Permeabilität setzen, da es einfach zu kompliziert wird und mit meinen Mitteln auch viel zu ungenau. Eventuell schreibe ich noch eine Universität an und frage einen Fachmann auf dem Gebiet des Magnetismus.
Was mir gerade noch einfällt. Ich könnte für den Hallsensor den einen Luftspalt zum Einführen des Sensors ja mit zum Beispiel 3 mm ausführen. Dann kann ich wohl die restlichen Luftspalte an den Kontaktstellen des Weicheisens vernachlässigen. Aber bei 3 mm Luftspalt geht mir µeff schon in den Keller und der Faktor um auf µr zurück zu rechnen wird sehr groß und ungenau. Ich hätte nicht gedacht, dass der an sich einfache Einstein-de Haas-Versuch dermaßen ausartet…
Inzwischen habe ich mich um den Spiegel + Halterung gekümmert. Als Ausgangsmaterial dienten ein DVD-Rohling und Lüsterklemmen. Dadurch bin ich bei der Ausrichtung des Spiegels sehr flexibel.

Ich habe auch den zu erwartenden Winkelausschlag ausgerechnet, wenn die Valenzelektronen des Weicheisenstabs durch das äußere Magnetfeld ausgerichtet werden. Jedes Elektron trägt ja dann einen Drehimpuls von 1/2·(h/2·π) zum Gesamtdrehimpuls Lges bei. Daraus lässt sich dann die Startwinkelamplitude φ0 berechnen:

Demnach beträgt die Startwinkelamplitude nur 0.018°. Befindet sich die Skala für den Laserstrahl in 3 m Abstand, so beträgt die Verschiebung des Auftreffpunkts lediglich 1.92 mm. Das wird wohl unter der Messgrenze meines Aufbaus liegen 🙁
Die Spule zur Erzeugung des Magnetfelds konnte ich heute auch wickeln. Ganz alleine ohne helfende Hand war dies aber alles andere als einfach und so entstand verständlicherweise kein Meisterwerk. Insgesamt sind es 3 Lagen auf 115 mm Länge. Mit dem Milliohmmeter habe ich dann den Widerstand des 0.6 mm Kupferlackdrahts zu 3.474 Ohm bestimmt. Ein Meter CuL-Draht besitzt einen Widerstand von 0.058 Ω. Damit kam ich auf eine Drahtlänge von rund 60 m und demnach auf n = 560 Windungen.




Setze ich nun alle vorhandenen Messwerte in die Formel zur Berechnung des Landefaktors g ein, erhalte ich:

Es fehlen also nur noch die Messwerte für die Spulenstromstärke I, die relative Permeabilität µr des Weicheisenstabs und die Startwinkelamplitude φ0. Stromstärke und Auslenkungswinkel erhalte ich aber erst nach Durchführung des Einstein-de Haas Versuchs. Bin neugierig, ob ich überhaupt eine Auslenkung des Laserstrahls beobachten kann.






Gestern konnte ich den ersten Testlauf starten. Leider verlief dieser in keinster Weise so wie erhofft. Erstens dauert es eine halbe Ewigkeit, bis der Weicheisenstab keine Schwingungen mehr um den Aufhängepunkt des Fadens vollführt (die Torsionsschwingung ist hingegen “relativ” bald abgeklungen) und schalte ich dann den Spulenstrom ein, wird der Weicheisenstab aufgrund seiner Magnetisierung und nicht ganz 100%iger Symmetrie bzw. auch nur minimaler Schieflage aus seiner Ruhelage gerissen. Dies macht es unmöglich, eine reine Torsionsbewegung um 1/10° zu beobachten. Ich müsste mit dem Strom auf ein Minimum (ca. 0.2 A) gehen und selbst dann pendelt der Weicheisenstab nach dem Einschalten des Stroms um eine andere Ruhelage als noch ohne Strom.

Daher werde ich es noch mit 2 Torsionsfäden probieren und den Weicheisenstab oben und unten damit fixieren. Halte ich die Fäden dann schön auf Zug, so hoffe ich die störenden radialen Bewegungen in den Griff zu bekommen. Mit nur einem Torsionsfaden ist das meiner Meinung nach ein Ding der Unmöglichkeit. Bei 1-2 A wird der Weicheisenstab komplett zur Innenwand der Spule gezogen und vollführt daher massive Störbewegungen. Den Spiegel gemacht aus einem kleinen Stück einer DVD muss ich auch noch gegen einen Oberflächenspiegel austauschen, da der Lichtfleck an der Wand mit DVD-Spiegel viel zu groß und unförmig ist.
Dieser Einstein-de Haas-Versuch entpuppt sich als wirklich extreme Herausforderung. Daran sieht man aber sehr schön den Unterschied zwischen Theorie und Praxis/Experiment. Theoretisch lässt sich dieser Versuch sehr einfach darstellen, experimentell ist er sehr herausfordernd wenn nicht gar unmöglich durchzuführen mit Hausmitteln. Aber mal schauen, aufgegeben habe ich noch nicht…






Der Weicheisenkern ist diese Woche eingetroffen und so konnte ich einige Messungen machen. Seine Abmessungen sind: dinnen = 30 mm daußen = 35 mm Höhe = 22 mm mittlerer Radius r = 16.25 mm Querschnittsfläche A = 55 mm². Ich habe ihn mit n = 92 Windungen versehen. Damit komme ich theoretisch auf eine Induktivität der Luftspule LLuft = 5.73 µH. Mit Weicheisenkern erhalte ich mit meinen Messgeräten stark unterschiedliche Werte und zwar:
- Multimeter mit Induktivitätsfunktion: LKern = 115 µH, was einer relativen Permeabilität µr = 20 entspricht
- Multifunktionsmesser: LKern = 10 µH ⇒ µr = ca. 2
- Dann habe ich noch den Spannungsstoß bei 4 Sekundärwindungen mittels Oszi ermittelt und daraus die relative Permeabilität µr ermittelt: Dies ergab ein µr = 88.
Wie man sieht, schwanken die Messwerte nicht nur stark, ich bin auch meilenweit von der echten Permeabilität im Bereich um die 1000-2000 entfernt!






Zum Test habe ich dann auch noch einen Ferritringkern (Modell FT 140-77) aus dem Material 77 bewickelt und zwar mit 76 Windungen. Seine Abmessungen sind: dinnen = 23 mm, daußen = 35.6 mm, Höhe h = 12.6 mm, mitterer Radius r = 14.65 mm und Querschnittsfläche A = 79.4 mm². Mit n = 76 Windungen komme ich für die Luftspule theoretisch auf eine Induktivität von LLuft = 6.26 µH. Mit Kern messe ich folgende Induktivitäten:
- Mit Multimeter mit L-Funktion: LKern = 11.69 mH ⇒ µr = 1867
- Mit kleinem Multifunktionstester: LKern = 50.82 mH ⇒ µr = 8117
- Die Methode mit dem Spannungsstoß und dessen zeitliche Integration ergab ein µr = 997
Der erste Wert passt aber sehr gut. Denn die Permeabilität des 77-Materials ist laut Datenblatt mit 2000 angegeben. Zusätzlich besitzt der Kern einen AL-Wert von 2250 nH/n². Bei n = 76 Windungen komme ich also laut Datenblatt auf eine Induktivität von rund 13 mH. Dies deckt sich nicht schlecht mit dem zuerst gemessenen 11.69 mH.
Fazit: Bei geschlossenen Ferritringen kann man also (abhängig vom Messgerät) doch recht gut die relative Permeabilität experimentell bestimmen. Beim Weicheisenkern, auch wenn dieser geschlossen ist in Form eines Rings, geht dies scheinbar überhaupt nicht. Der höchste experimentelle Messwert liegt bei rund 90, also wie schon gesagt sehr weit vom “echten” Wert entfernt. Gegenüber dem Weicheisenstab brachte die geschlossene Form des Weicheisens keine nennenswerte Verbesserung experimenteller Ergebnisse für µr. Die Wirbelströme scheinen also die Messung der Induktivität massivst zu beeinflussen.
Die lange Einkaufsliste für den Baumarkt ist schon geschrieben. Ich werde den gesamten Aufbau aus Holz fertigen. Den Weicheisenstab mehrfach zu durchbohren und mit Gewinden auszustatten ist auch nicht gerade einfach. Zu leicht reißt dabei der dünne Bohrer (1-2.5 mm) ab. Dann heißt es den Weicheisenstab zu kürzen und alles nochmals zu bohren. Eigentlich wollte ich ja das achsiale Loch für die 0.3mm Nylonschnur mit nur rund 0.5 mm ausführen. Das konnte ich aber schnell vergessen. Jetzt ist dieses halt an den Enden des Stabs 1.5 mm dick.

Die Nylonschnur werde ich oben und unten zwischen jeweils 2 Aluplatten einklemmen. Die obere Plattform kann ich dann über Flügelmuttern entlang der Gewindestangen höhenmäßig verstellen, sodass ich die Nylonschnur schön auf Zug bekomme. Die Erregerspule werde ich mit einer Rohrschelle umklammern und dann seitlich fixieren. Auf diese Weise kann ich die Position der Erregerspule gegenüber dem Weicheisenstab auch sehr schön vertikal verändern.

Den aus einer DVD gefertigten Spiegel habe ich inzwischen gegen einen schönen Oberflächenspiegel ersetzt. Damit wird der Laserpunkt deutlich besser zu lokalisieren sein.
Interessant ist der Originalartikel zum Einstein-de Haas-Effekt von den beiden Physikern: https://archive.org/details/verhandlungen00goog/page/n167/mode/2up?view=theater
Einstein und de Haas haben den Landefaktor g mittels der Resonanzkurve der erzwungenen Torsionsschwingung bestimmt. Das muss ich mir noch genauer anschauen. Vielleicht wäre dieser Zugang auch etwas für mich. Dann bräuchte ich aber einen einigermaßen leistungsfähigen Verstärker für das Signal vom Funktionsgenerator. Die Frage ist, ob ich dafür einen gewöhnlichen Audio-Verstärker https://www.neuhold-elektronik.at/catshop/product_info.php?products_id=7429 verwenden kann oder nicht. Immerhin müsste er sehr niedrige Frequenzen im Bereich 0.1 bis 2 Hz verstärken.
Die Halterungen für die Nylonschnur sind mittlerweile fertig:


Gestern konnte ich im Baumarkt (Hornbach) u.a. das Holz für das Stativ besorgen und zuschneiden lassen. Den finalen Aufbau übernimmt mein ältester Sohn, da ich keinen Bohrständer besitze und deshalb sämtliche Bohrungen nur nach Augenmaß bohren könnte. An den Enden der Pfeiler wird nämlich jeweils eine M6 Gewindestange versenkt, auf die dann die Deckplatte höhenverstellbar montiert wird.



Die flexible Halterung für den Laserpointer ist auch fertig:


Ich habe mich noch einmal mit der (Sättigungs)Magnetisierung von Eisen beschäftigt und folgendes Ergebnis erhalten:

Demnach tritt dann magnetische Sättigung ein, wenn pro Eisenatom rund 2 Elektronen ihr magnetisches Moment ausrichten. Valenzelektronen besitzt Eisen aber 8. Warum hier ein Unterschied besteht und nicht alle Valenzelektronen zur Magnetisierung beitragen, ist mir unklar…
Das Holzstativ ist soweit fertig. Ist jetzt keine handwerkliche Meisterleistung, aber es erfüllt seinen Zweck. Die Höhe der Holzpfeiler beträgt 98 cm, die Breiten 30 cm. Die Spulenhalterung habe ich jetzt auf halber Höhe postiert. Mittels der Flügelmuttern kann dann der Torsionsfaden schön gespannt werden. Dadurch erhöht sich auch das Richtmoment R und damit die Torsionsschwingungsfrequenz, was eigentlich kein Nachteil ist. Die Schwingungsfrequenz lag bei Einsteins Originalversuch bei um die 50 Hz. Meine liegt durch den massiven Weicheisenstab deutlich niedriger bei rund 0.3 Hz. Mal schauen, ob dies ein entscheidender Nachteil ist…







Hier noch die Abmessungen des Weicheisenstabs: d = 1 cm, l = 11.8 cm und m = 71.92 g.

Jetzt steht eigentlich einem ersten Versuch nichts mehr im Weg…
Der erste Testlauf ist vollbracht. Leider musste ich feststellen, dass die Fadenfixierung mit den M3-Madenschrauben im Weicheisenstab nicht gerade gut funktioniert. Mir ist jedesmal beim Spannen des Fadens dieser dort gerissen. Deshalb bin ich nun auf Kupferlackdraht gewechselt und habe diesen nicht mehr mit den Madenschrauben fixiert, sondern ihn einfach durch das Querloch geführt und dann verdrillt und verlötet.



Jetzt reißt er zum Glück nicht mehr. Aber der 0.4 mm Kupferlackdraht muss, um ordentlich gespannt zu sein, um die volle Länge der oben herausragenden Gewindestangen gedehnt werden. Um einen etwas widerstandsfähigeren/härteren Draht zu haben, verwende ich nun CuL mit 0.6 mm Durchmesser. Dieser lässt sich schon um einiges schwerer dehnen.
Die Torsionsschwingungen haben durch die hohe Spannung des Drahts und seinen größeren Durchmesser eine deutlich höhere Frequenz als noch mit dem Kunststofffaden. Diese habe ich einmal mittels Photodiode und dann mittels High-Speed-Kamera bestimmt. Ich komme bei allen 4 Messungen auf 10.8 – 11 Hz.



Die Methode mit der Casio-High-speed-Kamera ist aber wohl deutlich genauer und bequemer. Also werde ich künftig auf sie zurückgreifen. Mit der Periodendauer τ lässt sich dann wieder das Richtmoment R berechnen. Ich erhalte einen Wert von R = 0.0043 Nm/rad, also einen deutlich höheren Wert als noch mit der Nylonschnur als Torsionsfaden.
Spanne ich den Faden allerdings stärker, muss ich natürlich das Richtmoment neuerlich bestimmen. Aber auch für die Bestimmung der Dämpfung der gedämpften Schwingung (siehe weiter unten) kann ich die Casio-Kamera sehr gut gebrauchen. Hierfür muss ich ja die Abnahme der Winkelamplituden innerhalb einer bestimmten Zeit ermitteln.
Ergebnisse zur Variante 1:
Meine erste Spule hat sich durch thermische Überbelastung (10A über 2 Minuten waren dann doch zu viel) leider vom PVC-Rohr gewickelt. Daher musste eine neue her. Mit der sich viel zu schnell drehenden Bohrmaschiene ist das eigentlich eine unlösbare Aufgabe. Daher sieht meine zweite Spule auch alles andere als schön gewickelt aus:




Der in den Experimenten zum Einsatz kommende Weicheisenstab besitzt eine Länge von 11.8 cm und eine Masse von 71.92 g.

Hier der fertige Messaufbau:




Mittels der Casio-High-Speed-Kamera habe ich zunächst einmal die Periodendauer τ der unerregten Schwingung des Torsionspendels bestimmt. Ich kam auf eine Frequenz von ca. 10.5 Hz. Damit konnte ich das Richtmoment R zu 0.00385 Nm/rad berechnen.


Nach dem Einschalten (0.5 A Spulenstrom) konnte ich eine Schwingungsamplitude von 0.6 cm messen bei einem Abstand Spiegel-Wand von 3.5 m.

Mit diesen Ergebnissen konnte ich den Landefaktor g nach der Variante 1 berechnen:

 Leider liegt der erhaltene Wert mit 0.019 sehr weit vom tatsächlichen Wert 2 entfernt. Ein Hauptgrund dürfte sein, dass sich die Drehbewegung des Weicheisenstabs nicht nur durch die Ausrichtung der magnetischen Momente der Elektronen ergibt, sondern auch durch die Wechselwirkung des magnetisierten Stabs und der stromdurchflossenen Spule. Wenn man sich die obige Formel zur Variante 1 ansieht, müsste die tatsächlich gemessene Winkelamplitude φ0 viel kleiner sein als von mir gemessen. Der Laserstrahl kommt bei meinem Versuchsaufbau auch kaum zur (absoluten) Ruhe. Von daher wären kleinste Auslenkungen ohnedies nicht zu messen.
Leider liegt der erhaltene Wert mit 0.019 sehr weit vom tatsächlichen Wert 2 entfernt. Ein Hauptgrund dürfte sein, dass sich die Drehbewegung des Weicheisenstabs nicht nur durch die Ausrichtung der magnetischen Momente der Elektronen ergibt, sondern auch durch die Wechselwirkung des magnetisierten Stabs und der stromdurchflossenen Spule. Wenn man sich die obige Formel zur Variante 1 ansieht, müsste die tatsächlich gemessene Winkelamplitude φ0 viel kleiner sein als von mir gemessen. Der Laserstrahl kommt bei meinem Versuchsaufbau auch kaum zur (absoluten) Ruhe. Von daher wären kleinste Auslenkungen ohnedies nicht zu messen.
Es bleiben aber 2 weitere Varianten zur Messung des Landefaktors (siehe Abschnitt unten), welcher sich Einstein und de Haas in ihrem Originalexperiment 1915 bedienten.
Ich habe inzwischen den Originalartikel zum Einstein-de Haas Versuch aus dem Jahr 1915 durchgeackert. Dies war nicht gerade einfach, da u.a. heute nicht mehr gebräuchliche Symbole für diverse physikalische Größen verwendet wurden. Hier nun die von mir überarbeitete Anleitung:

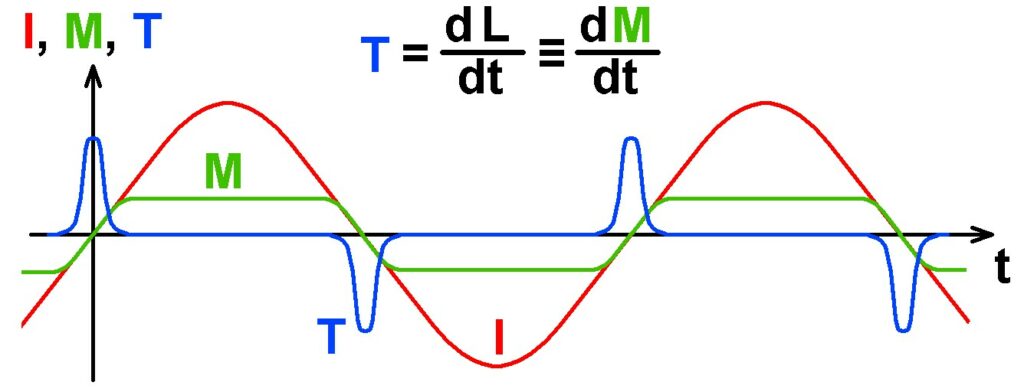









Einstein und de Haas führten den Versuch etwas anders ich durch und zwar speisten sie die Spule mit Wechselspannung in Resonanz bzw. variabler Frequenz. Dies führt nun für mich zu zwei weiteren Möglichkeiten, den Landefaktor g zu bestimmen.
Im ersten Fall speise ich die Spule genau mit der Resonanzfrequenz f0.
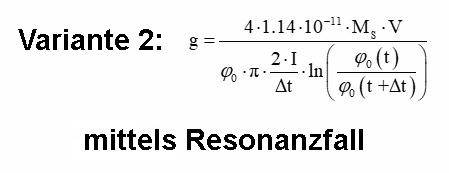 Bestimmt werden müssen dann nur der maximale Winkelausschlag φ0, das Trägeitsmoment I und das Volumen V des Weicheisenstabs, die Winkelamplitudenabnahme von φ0(t) nach φ0(t + Δt) innerhalb der Zeit Δt (sprich die Dämpfung der nicht mehr angeregten Schwingung, wenn der Spulenstrom abgeschaltet wurde), und die aus Büchern bekannte Sättigungsmagnetisierung MS, welche bei rund 1 500 000 A/m liegt (siehe auch Herleitung weiter oben).
Bestimmt werden müssen dann nur der maximale Winkelausschlag φ0, das Trägeitsmoment I und das Volumen V des Weicheisenstabs, die Winkelamplitudenabnahme von φ0(t) nach φ0(t + Δt) innerhalb der Zeit Δt (sprich die Dämpfung der nicht mehr angeregten Schwingung, wenn der Spulenstrom abgeschaltet wurde), und die aus Büchern bekannte Sättigungsmagnetisierung MS, welche bei rund 1 500 000 A/m liegt (siehe auch Herleitung weiter oben).
Bei der zweiten Variante nimmt man die Resonanzkurve auf, sprich man bestimmt die Winkelamplitude φ0 in Abhängigkeit von der Erregerfrequenz f. Daraus lässt sich dann für mehrere Messpaare (f, φ0) der Landefaktor g berechnen. Man wird hier den Mittelwert bilden.


Benötigt werden also neben den Messpaaren (f, φ0) das Trägheitsmoment I und das Volumen V des Weicheisenstabs, die Elektronenmasse m und die Elementarladung e, die aus der Literatur bekannte Sättigungsmagnetisierung MS in der Höhe von ca. 1 500 000 A/m, die Winkelamplitude φ0,max und die Frequenz f0 im Resonanzfall.
Ich benötige also für die experimentelle Bestimmung des Landefaktors g nach den beiden Varianten von Einstein und de Haas eine AC-Ansteuerung der Spule mit variabler Frequenz. Aus diesem Grund habe ich mir einen Leistungsoperationsverstärker vom Typ OPA549 gekauft. Dieser kann mit maximal +/- 30 V versorgt werden und die maximale Stromstärke beträgt 8 A. Bei einer Speisung von +/- 20 V und einem Spulenwiderstand von rund 3-4 Ω reize ich also den OPV strommäßig sehr gut aus.
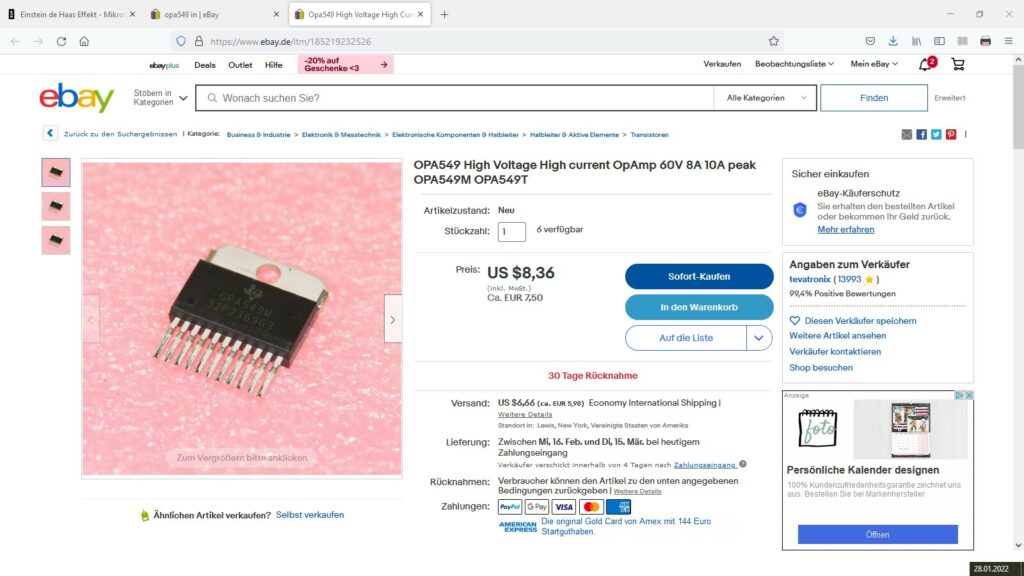





Beim ersten Testlauf habe ich mir leider mit dieser Schaltung mein Smartphone geschrottet, da das Kabel mit der max. 15V Ausgangsspannng versehentlich mein Buchsenkabel zum Smartphone berührt hat 🙁
Wie man sieht, funktioniert aber der Verstärker sehr gut und liefert mir max. Amplituden von +/- 18V.


Ergebnisse zur Variante 2:
Bei dieser Variante zur Berechnung des Landefaktors g wird der Weicheisenstab mit seiner Resonanzfrequenz zu Torsionsschwingungen angeregt. Die sich einstellende Winkelamplitude φ0 und danach die exponentielle Abnahme der Winkelamplitude wird für die Formel benötigt. Die Schwingungsamplitude auf der Wand betrug bei der Resonanzfrequenz von 10.436 Hz genau 18.4 cm. Für die Erfassung der exponentiellen Abnahme verwendete ich die Software Tracker.



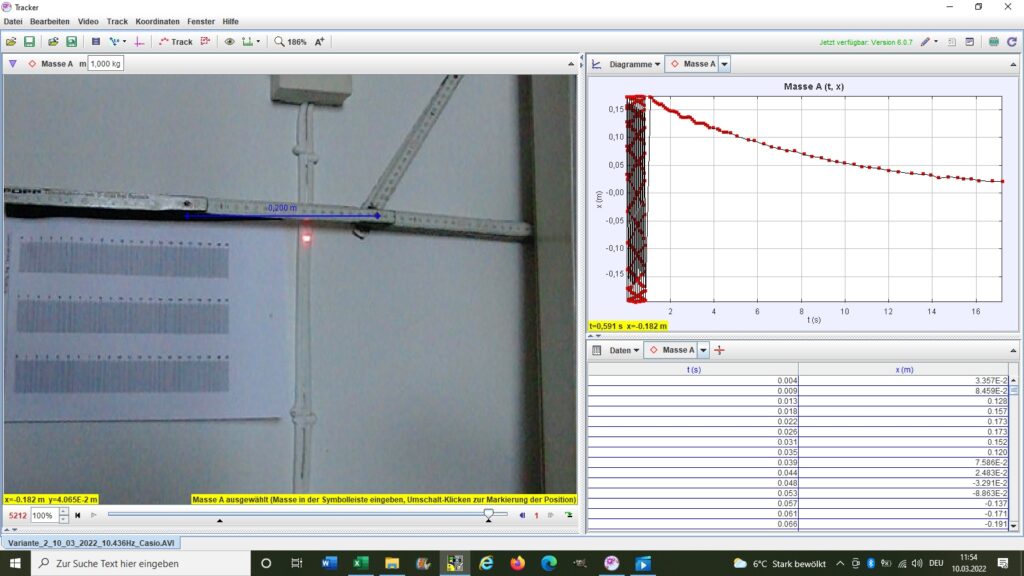
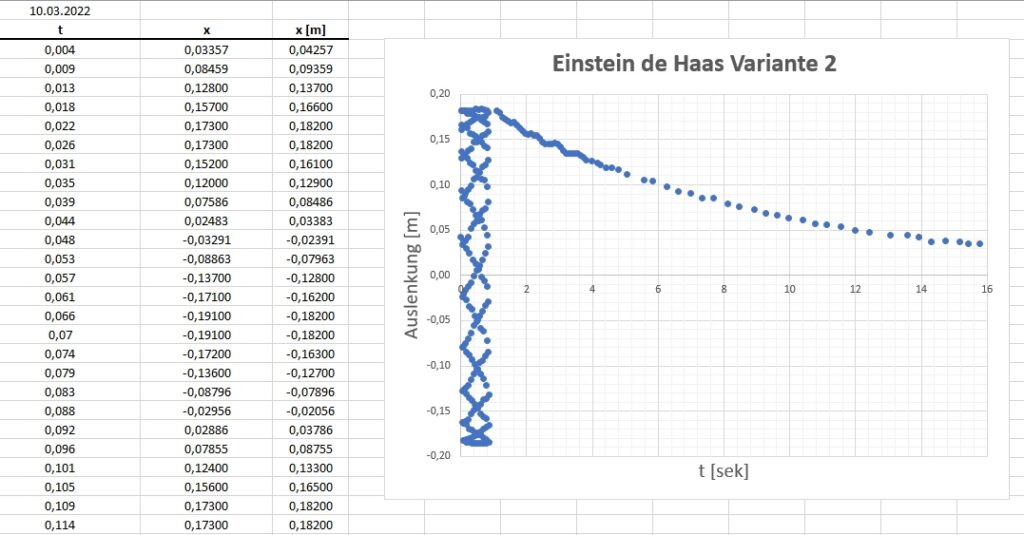
Hier nun das Ergebnis für den Landefaktor nach Variante 2:

Leider ist auch der mit dieser Variante ermittelte Wert für g viel zu klein. Er sollte wie gesagt bei 2 liegen! Was mich irritiert ist folgender experimenteller Umstand: Bei dieser Variante wird eigentlich nur die Winkelamplitude φ0 und die exponentielle Abnahme der Schwingung benötigt.
Es zeigte sich aber experimentell, dass meine Winkelamplitude φ0 extrem stark von der Spulenspannung abhängt. Steigere ich die an der Spule anliegenden Spannungsamplitude, so nahm auch die Winkelamplitude sehr stark zu. Im Falle der magnetischen Sättigung hätte eigentlich die Spannungsamplitude der Spule ab einem gewissen Wert keinen Einfluss mehr auf die Winkelamplitude. Dies bedeutet, dass ich in obige Formel auch ohne weiteres größere Winkelamplituden φ0 einsetzen hätte können, wenn ich die Ansteuerung der Spule erhöht hätte. Richtigerweise hätte ich wohl diese solange erhöhen müssen, bis sich die Winkelamplitude nicht mehr erhöht hätte. Erst dann wäre wohl magnetische Sättigung eingetreten. Dies bedeutet aber, dass der “richtige” Wert für φ0 noch viel größer als der letztendlich in die Formel eingesetzte Wert von 0.0263 rad gewesen wäre. In weiterer Folge wäre dann der berechnete Landefaktor noch kleiner gewesen als er ohnedies schon ist. Alles nicht ganz einfach…
Ergebnisse zur Variante 3:
Was macht ein normaler Mensch am Sonntag? Richtig, er experimentiert…
Heute konnte ich den Landefaktor mittels der dritten Variante bestimmen. Dazu nimmt man die Resonanzkurve auf, sprich man bestimmt den Winkelausschlag in Abhängigkeit von der Erregerfrequenz. Die Resonanzfrequenz lag bei rund 10.50 Hz. Bei dieser Frequenz war die erregte Schwingung maximal. Darüber bzw. darunter nimmt die Schwingung des Resonators stark ab. Diese Resonanzkurve konnte ich eigentlich sehr gut experimentell ermitteln (siehe Abbildung) und dann für jede Erregerfrequenz einen in der Formel des Landefaktors vorkommenden Faktor berechnen.






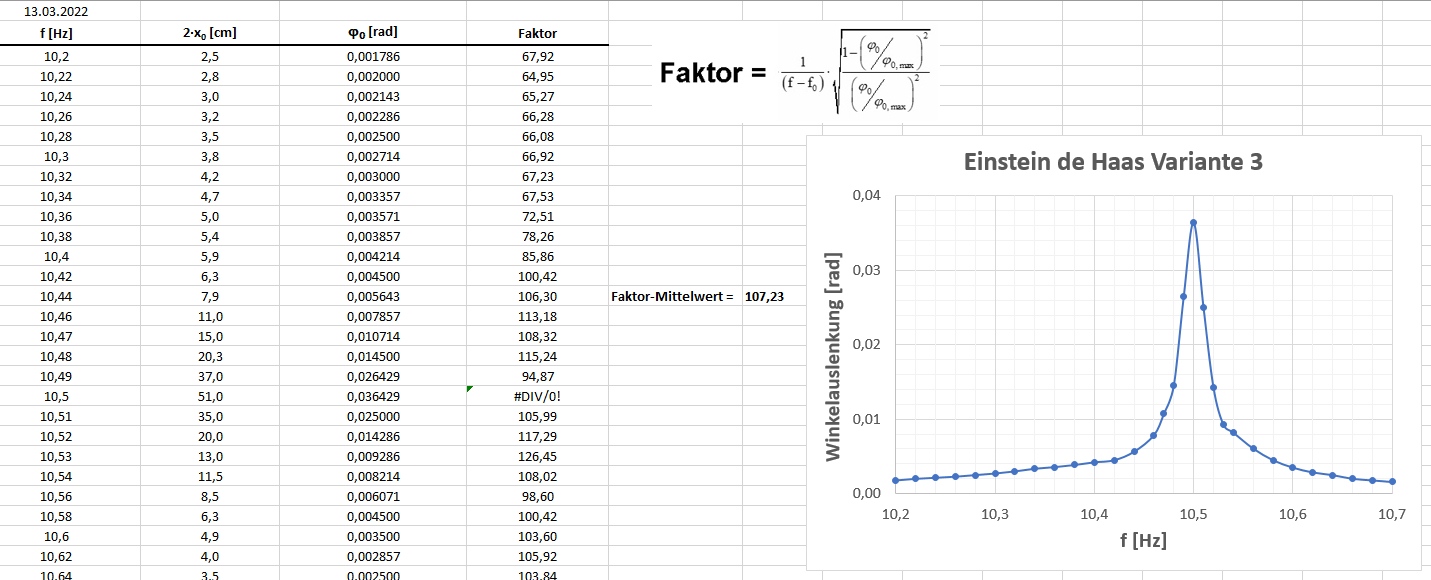
Wie man anhand der Tabelle sieht, war dieser Faktor für den Bereich um die Resonanzfrequenz ziemlich konstant und lag bei um die 107 sek. Bei Einstein und de Haas war dieser Faktor auch in ähnlicher Art um den Resonanzpunkt herum konstant. Mit diesen Mittelwert berechnete ich dann den Landefaktor und kam auf einen Wert von 0.0525.

Das ist zwar geringfügig besser als mit der Variante 1 und 2, wo er ja bei 0.019 bzw. 0.033 lag, aber noch meilenweit vom theoretischen Wert 2 entfernt.
Fazit: Der Landefaktor lässt sich nur sehr ungenau mit meinem Aufbau bestimmen. Dies war so ziemlich der aufwendigste Versuch, den ich bisher durchgeführt habe. Zu Beginn hätte ich mir dies bei der prinzipiellen Einfachheit des Versuchs nicht gedacht. Umso mehr bewundere ich die Physiker, die vor 100 Jahren oder mehr mit doch sehr einfachen Mitteln physikalische Größen oft sehr genau bestimmten.
Obwohl ich den Versuch zeitweise schon verflucht habe, bin ich dennoch froh, ihn durchgezogen zu haben. Es stehen eventuell noch einige Verbesserungen aus. So würde ich jetzt im nachhinein die Fadenlänge deutlich kürzer wählen. Ein kürzerer Draht würde nämlich weniger zur Seite ausgelenkt werden, als dies bei meiner Länge von rund 1 m der Fall war. Weiters würde ich es mit einem kürzeren Weicheisenstab probieren, der sich dann wirklich nur im homogenen Teil des Magnetfelds innerhalb der Spule befinden würde. Ob ich dies noch durchführe, weiß ich noch nicht. Jetzt bin ich einmal froh, überhaupt solche Ergebnisse erzielt zu haben. In diesem Sinne bleibt neugierig und Heureka…
Das Video reiche ich natürlich noch nach…

