Widerstände sind wenn nicht das wichtigste Elektronikbauteil. Es gibt Widerstände, die ihren Wert weitestgehend beibehalten (Ohmscher Widerstand) und welche, deren Wert zum Beispiel von der Temperatur (PTC, NTC), dem Lichteinfall (LDR) oder der anliegenden Spannung (VDR) abhängt.
Simon Georg Ohm (1789 – 1854)
Bildquelle: Wikipedia
Die Einheit des Widerstands ist Ohm, benannt nach Georg Simon Ohm. Das wohl wichtigste Gesetz der Elektronik, das sog. Ohmsche Gesetz, verknüpft die drei Grundgrößen Spannung U, Stromstärke I und Widerstand R:
Die Kennlinien eines ohmschen Widerstands (R = konstant) und für den Fall, wenn R sich ändert:
PTC und NTC-Widerstände verändern ihren Widerstand R in Abhängigkeit von der Temperatur. PTC steht für positiver Temperaturkoeffizient. Dies bedeutet, das R mit zunehmender Temperatur T wächst. Bei NTC-Widerständen ist es genau anders, hier sinkt mit zunehmenden T der Widerstand. Schließt man einen solchen PTC- bzw. NTC-Widerstand an ein Netzteil und erhöht die Spannung, so führt der durch den Widerstand fließende Strom zu einer zunehmenden Erwärmung. Die Kennlinie eines PTC-Widerstands (z.B. eine Glühbirne) müsste also der roten Kurve oben entsprechen. Die Kennlinie eines NTC-Widerstands hingegen der grünen Kurve.
Auf aliexpress habe ich NTC-Widerstände gekauft. Diese sind mittlerweile angekommen und so konnte ich die Kennlinie eines ohmschen Widerstands, eines NTC- und eines PTC-Widerstands aufnehmen.
Zuerst der ohmsche Widerstand (R = konstant), gebildet aus 3 parallel verschalteten 100Ω/100W Widerständen:
Wie zu erwarten entspricht die Kennlinie einer ansteigenden Geraden mit dem Anstieg k = 1/R:
Als PTC-Widerstand kam wie schon gesagt eine Glühbirne zum Einsatz:
Die Kennlinie I = I(U) eines PTC-Widerstands flacht mit zunehmender Spannung immer mehr ab. Genau dies konnte experimentell bestätigt werden:
Zum Schluss die Kennlinie eines NTC-Widerstands mit einem Nennwiderstand von 50 Ohm bei Zimmertemperatur:
Abgebildet ist hier ein NTC-Widerstand mit 20 Ohm bei Zimmertemperatur (siehe Aufdruck):
Die Kennlinie des NTC-Widerstands steigt immer stärker an:
Das Problem bei der Messung bestand darin, dass der Strom I nicht konstant blieb sondern während der Messung immer schneller stieg. Warum ist dies so? Nun, der Strom durch den NTC-Widerstand erwärmt diesen und dessen Temperatur steigt. Damit sinkt aber sein Widerstand R. Demzufolge steigt die Stromstärke I an und erwärmt den NTC-Widerstand noch stärker. Seine Temperatur wächst also weiter und sein Widerstand sinkt fortlaufend. Dieser Kreislauf führt zu einem mit der Zeit immer stärker und schneller anwachsenden Strom, sodass bei einer bestimmten Spannung U kein genauer Strom I gemessen werden kann.
Von welchen Faktoren hängt nun der Widerstand R eines Drahts ab? Sicher einmal von seiner Geometrie. Je länger der Draht ist, umso höher ist sein Widerstand. Und je dicker der Draht, umso geringer der Widerstand. Das Material spielt dann natürlich auch noch eine entscheidende Rolle. Es gilt folgende Gesetzmäßigkeit:
Der spezifische Widerstand ρ ist vom Material abhängig. ρ wird gleich R für L = 1 m und A = 1 m².
Demnach wird der spezifische Widerstand ρ bei Metallen einen sehr kleinen Wert besitzen, denn ein so kurzer und dicker Draht besitzt mit Sicherheit nur einen minimalen Widerstand R = ρ. Hier eine Tabelle mit den spezifischen Widerständen einiger Stoffe:
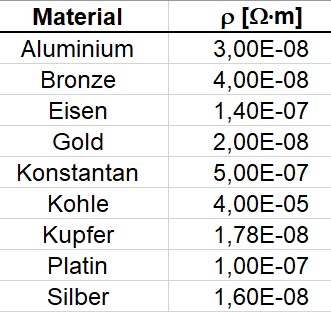
Wie man sieht, besitzt Kupfer einen sehr geringen spezifischen Widerstand. Deshalb verwendet man dieses Metall auch vorwiegend für Kabel. Durch seine Kleinheit ist der spezifische Widerstand von Metallen aber gar nicht so einfach experimentell bestimmbar. Gewöhnliche Multimeter messen im Ohm-Bereich nicht so kleine Widerstände. Es gibt aber eine sehr einfache und elegante Möglichkeit, Widerstände im mΩ-Bereich zu messen. Man benötigt nur eine Konstantstromquelle und ein Multimeter. Hier eine Variante mit dem LM317-Spannungsregler:
Der LM317 regelt in dieser Schaltung die Spannung immer so nach, dass ein Strom von I = 1 A durch den Prüfling fließt. Für den Spannungsabfall an diesem gilt dann: U = I·R = 1·R = R. Der Spannungsabfall U entspricht also genau dem ohmschen Widerstand des z.B. Kabels. Da Multimeter ohne Schwierigkeiten Spannungen im Millivolt-Bereich erfassen können, können mit dieser Variante auch Milliohm gemessen werden. Beispiel Kabelwiderstand:
Das einzelne 1 m lange Kabel besitzt also einen Widerstand R = 34.7 mΩ.
Zwei dieser Kabel parallel müssten also den halben Widerstand ergeben, was mit R = 17.6 mΩ auch annähernd der Fall ist. Diese Messmethode nennt man 4-Leiter-Messung. Da mit den Klemmen sowohl der Strom eingekoppelt, als auch die Spannung gemessen werden muss, eignen sich solche günstig auf ebay zu beziehenden Klemmen:
Was macht man aber, wenn der Leiter kein Draht ist, sondern eine andere geometrische Form besitzt? Nehmen wir an, wir hätten einen Widerstandskeil vor uns:
Gesucht ist also der Widerstand R(x) in Abhängigkeit von x. Da der Keil in diesem Fall zusammenläuft, wird der Widerstand mit zunehmendem x durch den kleiner werdenden Querschnitt A immer stärker steigen. Der Graph wird also in etwa folgende Form besitzen:
Man kann die Funktion R(x) aber auch konkret berechnen. Ausgangspunkt ist wieder die obige Beziehung R = ρ·L/A:
Damit die Widerstände nicht viel zu klein sind, wird man beim Experiment einen möglichst dünnen Widerstandskeil verwenden. Ich habe mich konkret für einen Graphit-Leitlack entschieden, den ich ganz dünne auf einen Träger aufsprühe.
Kenne ich dann die Messwerte R(x) kann ich mittels Excel die Schichtdicke h so anpassen, dass die theoretischen Werte bestmöglich mit den experimentellen übereinstimmen.
Der Graphitlack ist inzwischen angekommen und so konnte ich den Widerstandskeil mit dem Spray erstellen:
Die beiden Abgriffe habe ich mit zwei Messingstäben realisiert:
Mit dem Multimeter messe ich Widerstände im niedrigen kΩ-Bereich. Um eine gute Übereinstimmung Experiment-Theorie zu erzielen, muss ich in Excel eine extrem geringe Schichtdicke von nur 6 nm wählen. Dies entspricht natürlich nicht der tatsächlichen Schichtdicke, denn diese ist bestimmt um einiges dicker. Daher bleibt nur übrig, dass der Graphitlack deutlich schlechter leitet als reiner Graphit, von dem ich ja bei der Simulation ausgegangen bin. Die beiden Kurven stimmen aber von der unrealistischen Schichtdicke einmal abgesehen sehr gut überein:
Eine nette Spielerei mit Widerständen hätte ich noch auf Lager und zwar geht es um ein Widerstandsnetzwerk mit theoretisch unendlich vielen Widerständen. Zuerst beginnt man mit einem einzelnen Widerstand:
Nun fügt man weitere 3 gleiche Widerstände wie abgebildet hinzu:
Dieses Spiel wiederholt man nun mehrmals und fügt jeweils drei weitere Widerstände hinzu:
Anhand der Messwerte kann man bereits vermuten, dass der Gesamtwiderstand einen bestimmten Grenzwert besitzt, dem er sich sukzessive mit steigender Stufenzahl nähert. Wie kann man diesen Grenzwert aber berechnen? Nun, es gilt wohl dieses Ersatzschaltbild:
Man kann also die gesamte Schaltung mit Rges so wie rechts abgebildet an die drei Widerstände anhängen. Mit dieser Idee lässt sich der Gesamtwiderstand dann sehr einfach berechnen:
Theoretisch müsste die Schaltung bei unendlich vielen Stufen also einen Gesamtwiderstand von 7321 Ohm besitzen. Dies deckt sich recht gut mit dem experimentellen Ergebnis:
Zum Schluss noch das Youtube-Video:
