Das nach Max Planck (1858–1947) benannte Wirkungsquantum spielt in der Quantenphysik eine zentrale Rolle, sei es bei der Heisenbergschen Unschärferelation oder der Photonenenergie E = h·f.
Variante 1:
Diese Naturkonstante lässt sich mittels Leuchtdioden (LED) sehr einfach bestimmen/abschätzen. Hierzu sind nur folgende Teile notwendig:
- LEDs in verschiedenen Farben
- fein regelbares Netzteil 0-5 V
- Amperemeter und Voltmeter
- einen 100 Ohm Vorwiderstand
Der Schaltplan sieht wiefolgt aus:
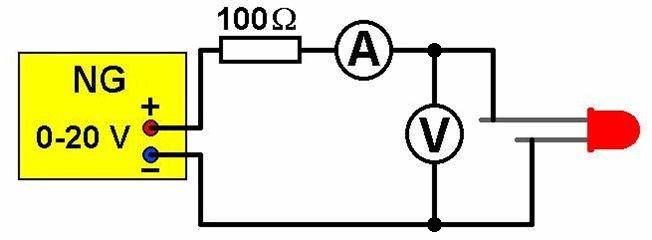
Die Spannung U wird nun in kleinen Schritten erhöht und jeweils der Strom I gemessen. Es wird sodann jene Spannung U_Schwelle notiert, bei der das erste Mal ein sehr schwaches Leuchten der LED beobachtet wird. Hierzu muss man mit dem Auge sehr nahe an die LED und diese eventuell mit einem Rohr aus schwarzen, dicken Papier umschließen.
Beispiel für die Kennlinie einer grünen LED:

Zwischen der Schwellspannung USchwelle und der Wellenlänge λ der verwendeten LED besteht folgender Zusammenhang:
USchwelle · e = h · f = h · c / λ
Aufgelöst nach h ergibt sich:
h = U_Schwelle · e · λ / c
Konkret konnte bei der grünen LED (λ = 540 nm) bei USchwelle = 1.8 V ein ersten Leuchten beobachtet werden. Eingesetzt in obige Formel liefert dies folgenden Wert für das Plancksche Wirkungsquantum:
h = 1.8 · 1.6 · 10^ –19 · 540 · 10^ –9 / 3 · 10 ^ 8 ≈ 5.2 · 10^ –34 Js
Der richtige Wert für das Plancksche Wirkungsquantum liegt bei 6.63 · 10^ –34 Js.
Wie man an der Formel für h erkennen kann, besitzt eine LED mit kleinerer Wellenlänge λ eine größere Schwellspannung USchwelle. Eine rote LED beginnt also bereits bei niedriger Spannung zu leuchten, eine blaue erst bei höherer Spannung!
Variante 2:
Eine andere Variante zur Bestimmung des Planckschen Wirkungsquantums verwendet einen Bauteiletester. Dieser kann um wenige Euro auf ebay erstanden werden.

Schließt man eine LED an den Bauteiletester an, so zeigt dieser die Flussspannung Uf an. Diese ist im Prinzip gleichbedeutend mit der obigen Schwellspannung USchwelle.


Nun bestimmt man für verschiedene LEDs, deren Wellenlänge λ zumindest einigermaßen genau bekannt sein muss, deren Flussspannung Uf.



Danach trägt man die Flussspannung Uf in Abhängigkeit von der Lichtfrequenz f = c / λ auf. Es sollte sich eine Gerade ergeben.
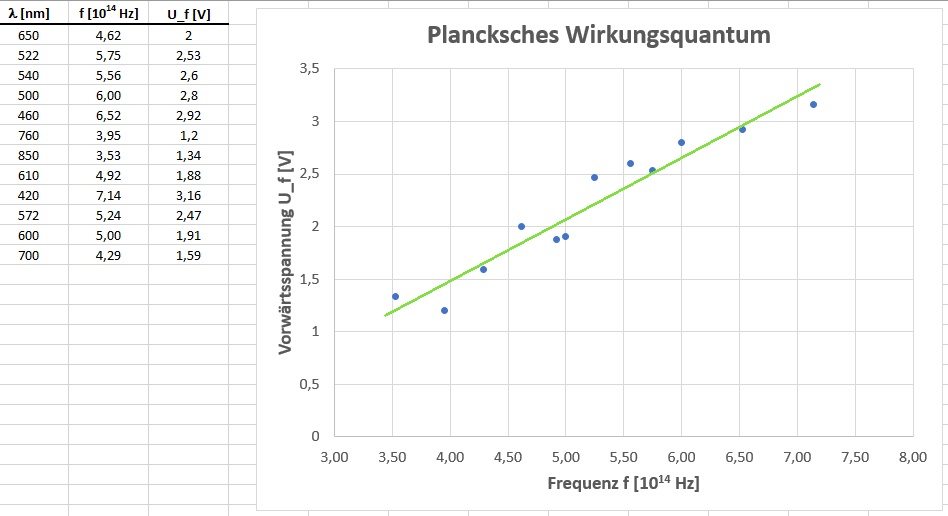
Zum Schluss bestimmt man von der Ausgleichsgeraden den Anstieg k = Gegenkathete / Ankathete.

Es gelten nun folgende Beziehungen:

Variante 3:
Ich wollte noch ein kompaktes Gerät mit integrierter Spannungsversorgung zur Bestimmung des Planckschen Wirkungsquantums haben. Herausgekommen ist dabei das hier:



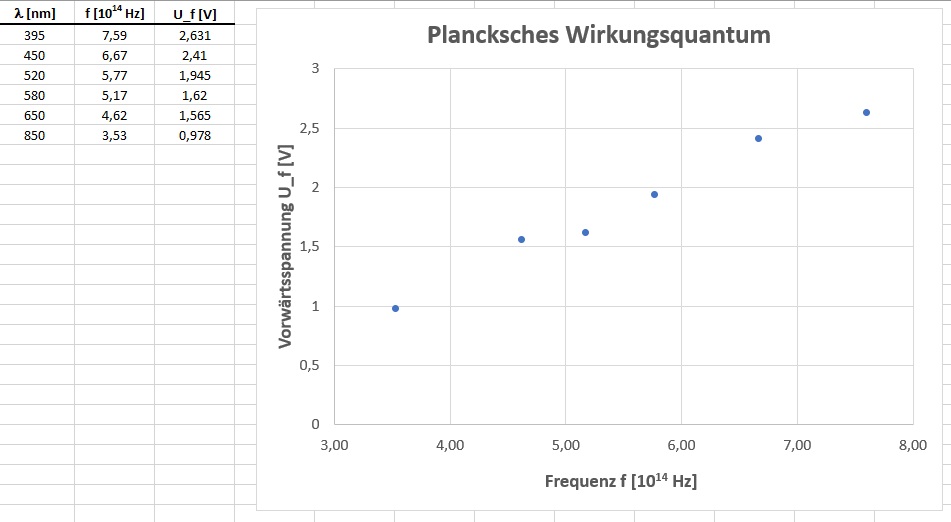
Zum Messablauf: Die Versorgungsspannung wird solange reduziert, bis der Strom auf Null zurückgegangen ist. Dies wird mittels Spannungsabfall am 220 Ω Vorwiderstand ermittelt. Sodann misst man die an der LED abfallende Spannung. Dies wiederholt man mit allen 6 LEDs.


Zur Auswertung wird die Flussspannung in Abhängigkeit von der Frequenz aufgetragen und der Anstieg k der Ausgleichsgeraden bestimmt. Für das Plancksche Wirkungsquantum h folgt dann einfach h = Anstieg k · Elementarladung e. Konkret erhalte ich einen Wert h = 6.59 · 10 ^ -34 Js. Die Abweichung zum Sollwert (6.63 · 10 ^-34) ist minimal.


Variante 4:
Im Internet (https://iitr.ac.in/Academics/static/Department/Physics/BTech%201st%20year%20lab/11_Plancks_Constant.pdf) bin ich auf eine weitere Methode gestoßen, das Plancksche Wirkungsquantum experimentell zu ermitteln und zwar mittels einer Solarzelle.
Der Aufbau ist einfach: Man hängt eine Glühbirne an ein Netzgerät mit der Spannung U und der Stromstärke I. Diese Glühbirne strahlt dann durch einen Schmalbandfilter auf eine Solarzelle. Der Abstand und die Ausrichtung der Solarzelle gegenüber der Glühbirne muss während des gesamten Versuchs unverändert bleiben!

Man misst nun mit einem Amperemeter den Kurzschlussstrom Θ der Solarzelle in Abhängigkeit von der Temperatur des Glühfadens. Dessen Temperatur bestimmt man über den angestiegenen Widerstand R = U/I der Glühwendel in Relation zum Widerstand bei Raumtemperatur.




Für die spektrale spezifische Ausstrahlung M(λ, T) eines Schwarzkörpers der absoluten Temperatur T und der Fläche dA im Wellenlängenintervall [λ, λ + dλ] gilt nach dem berühmten Planck‘schen Strahlungsgesetz:
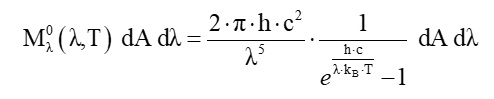

Strahlt der Schwarzkörper (Glühbirne mit der Oberfläche dA = A) auf eine Solarzelle in gleichbleibender Anordnung (Detektorfläche, Entfernung und Ausrichtung), so kommt nur ein bestimmter Prozentsatz k der spektralen spezifischen Ausstrahlung bei dieser an. Es gilt also für die bei der Solarzelle ankommende spektrale Strahlungsleistung:

Der Faktor k trägt eben der konkreten Geometrie Rechnung. Bleibt diese aber während des Experiments gleich, so kann k als Konstante betrachtet werden. Die gesamte aufgenommene Strahlungsleistung ist dann das Integral über den Spektralbereich. Befindet sich zwischen Glühbirne und Solarzelle ein Filter, gilt für diese von der Solarzelle aufgenommenen Gesamtstrahlungsleistung:

Diese Leistung führt zu einem proportionalen Kurzschlussstrom q der Solarzelle. Für den Kurzschlussstrom der Solarzelle muss dann aber noch ein spektraler Umwandlungsfaktor U(λ) berücksichtigt werden, denn Intensitäten in unterschiedlichen Spektralbereichen erzeugen unterschiedlich starke Photoströme (vgl. Empfindlichkeitskurve der Solarzelle bzw. Quantenausbeute). Daraus folgt:

Handelt es sich beim Filter um einen Schmalbandfilter, welcher nur einen kleinen Wellenlängenbereich um λ0 durchlässt, so kann das Integral näherungsweise gelöst werden. Es gilt dann:
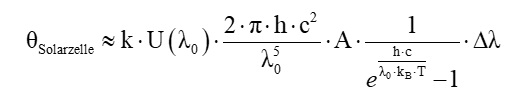
Δλ ist dabei die Breite des vom Filter durchgelassenen Spektralbereichs. Für sichtbares Licht (λ = 650 nm) und Temperaturen zwischen 1000 °C und 3000 °C gilt:

Für den Kurzschlussstrom der Solarzelle folgt daher näherungsweise:

In diesem Experiment misst man nun den Kurzschlussstrom Θ in Abhängigkeit von der Temperatur T der Glühbirne. Bildet man den natürlichen Logarithmus von Θ, erhält man:

Es folgt daraus weiter:
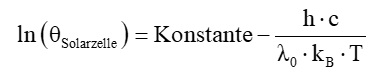
Trägt man im Graph ln(Θ) gegenüber 1/T auf, so müsste man eine fallende Gerade erhalten mit dem Geradenanstieg kGerade:


In diesem Faktor für den Geradenanstieg kGerade befinden sich bis auf das zu bestimmende Wirkungsquantum h lauter bekannte Größen. Es folgt also schlussendlich für das Planck’sche Wirkungsquantum:

Die Schmalbandfilter habe ich günstig auf ebay.com gekauft und mich für einen roten um λ = 650 nm bzw. einen für Infrarot um λ = 785 nm entschieden. Jener für Infrarot hat eine noch geringere Halbwertsbreite (10 nm) und dürfte daher besser für das Experiment geeignet sein…

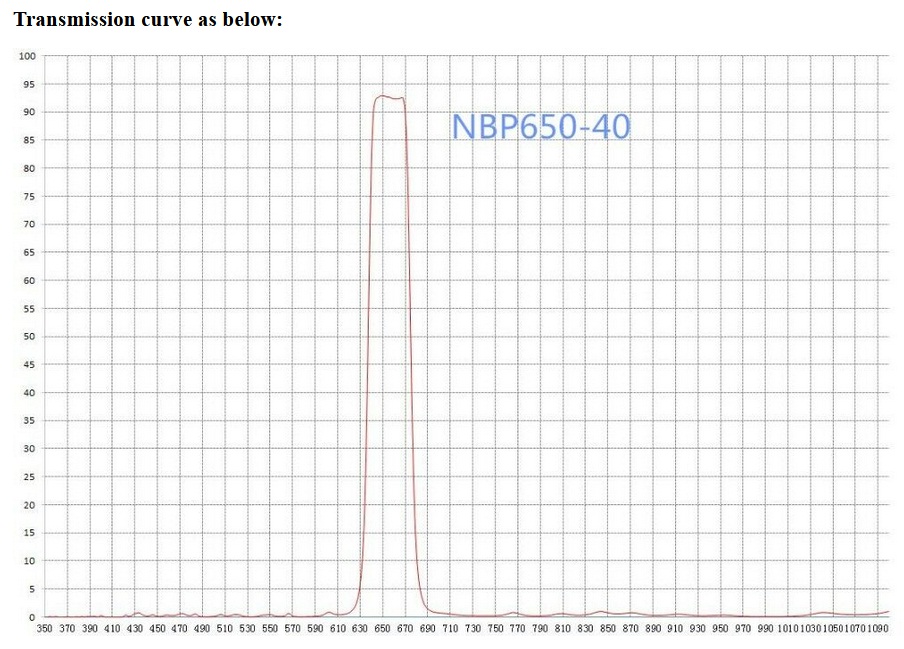

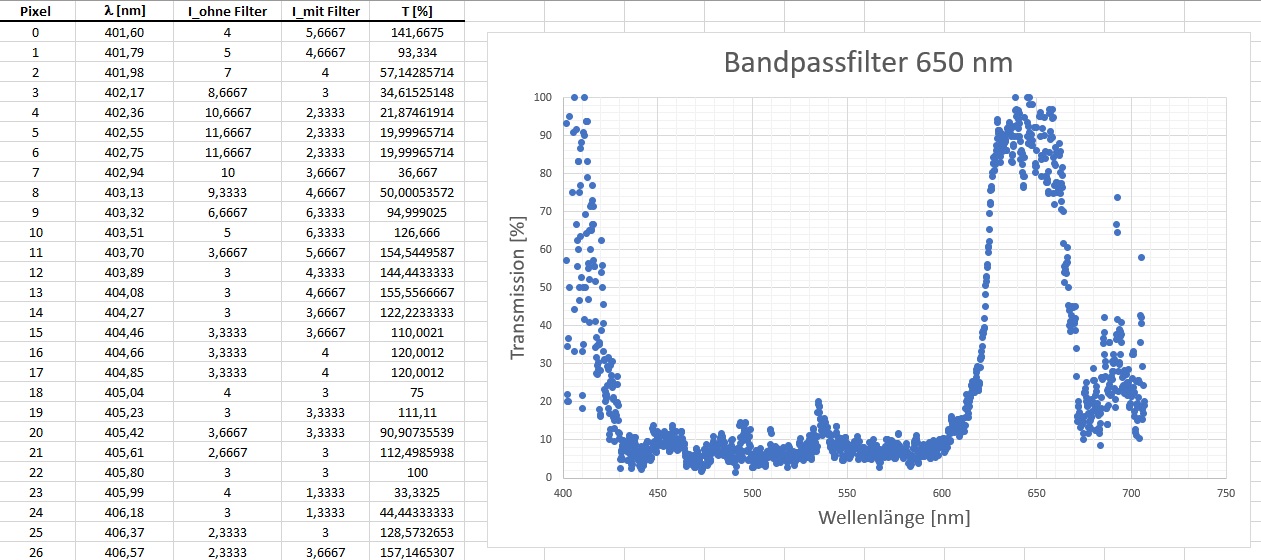
In der Zwischenzeit sind die Filter angekommen und ich habe das Transmissionsspektrum des 650nm-Filters mit meinem Webcamspektroskop aufgenommen. Es deckt sich eigentlich recht gut mit jenem oben vom Verkäufer. Für das Transmissionsspektrum des 785nm-Filters war mein Spektroskop leider nicht geeignet, da dieses nur bis ca. 707 nm geht.




Hier das Spektrum ohne Filter…

… und hier mit dem Schmalbandfilter

Durch Division der Intensiäten Imit Filter/Iohne Filter erhält man die Transmission T in Abhängigkeit von der Wellenlänge:
Der gesamte Aufbau fürs Experiment ist überschaubar und besteht aus „Glühbirnennetzteil“, Filter, Solarzelle und µA-Meter (https://stoppi-homemade-physics.de/nano-pikoamperemeter/). Letzteres deshalb, weil die Kurzschlussströme im µA-Bereich lagen…






Das Experiment wurde natürlich im Dunkeln durchgeführt, damit nicht das Umgebungslicht bereits für einen Kurzschlussstrom sorgt.


Hier nun die Ergebnisse bzw. die Graphen ln(Θ) in Abhängigkeit von 1/T. Zunächst für den 650nm-Filter


und dann noch für den 785nm-Filter


Wie zu erwarten war, liegt das Ergebnis für das Plancksche Wirkungsquantum h beim 785nm-Filter näher am Sollwert, da dieser Filter mit 10nm-Halbwertsbreite schmalbandiger ist als der 650nm-Filter (40nm Halbwertsbreite). Ich bin mit dem Ergebnissen eigentlich zufrieden, vor allem freue ich mich eine weitere Methode zur Bestimmung von h entdeckt zu haben 😉
Zum Abschluss noch das Youtube-Video:

