Quantenmechanische Beispiele, welche mit Schülern an Gymnasien durchgerechnet werden können, gibt es aufgrund ihres Schwierigkeitsgrades nicht viele. Eines davon ist die Berechnung der Energieniveaus im Wasserstoffatom.

Bildquelle: https://de.wikipedia.org/wiki/Niels_Bohr#/media/Datei:Niels_Bohr.jpg
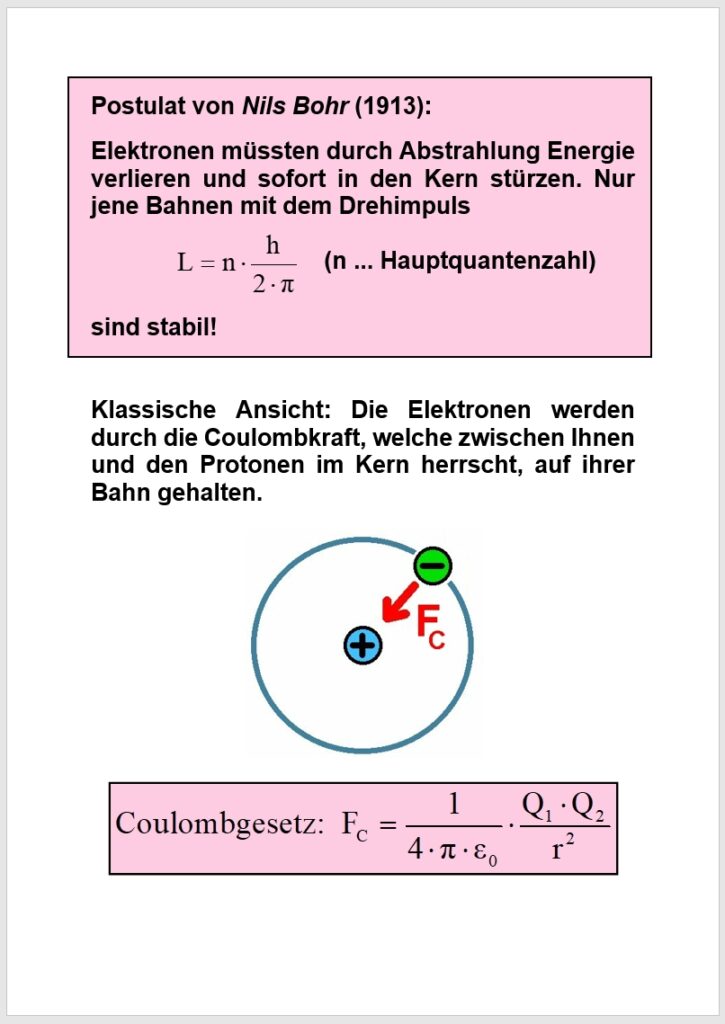
Die Basis der Rechnung bildet die vom Physiker Niels Bohr (1885 – 1962) postulierte Quantisierung des Drehimpulses L. Danach setzt man die für eine Kreisbewegung notwendige Zentripetalkraft gleich der Coulombkraft zwischen Elektron in der Hülle und Proton im Kern.




Dieses theoretisch hergeleitete Ergebnis lässt sich auch mit den Schülern experimentell überprüfen. Hierzu benötigt man nur eine Wasserstoff-Spektralröhre und eine Hochspannungsquelle. Die mit Wasserstoff gefüllte Entladungsröhre konnte ich um ca. 30 Euro in Wien/Österreich erwerben.

Zu deren Betrieb benötigt man noch eine Hochspannungsquelle, welche um die 1-2 kV/10mA liefern sollte. Hierfür eignet sich sehr gut ein CCFL-Inverter.
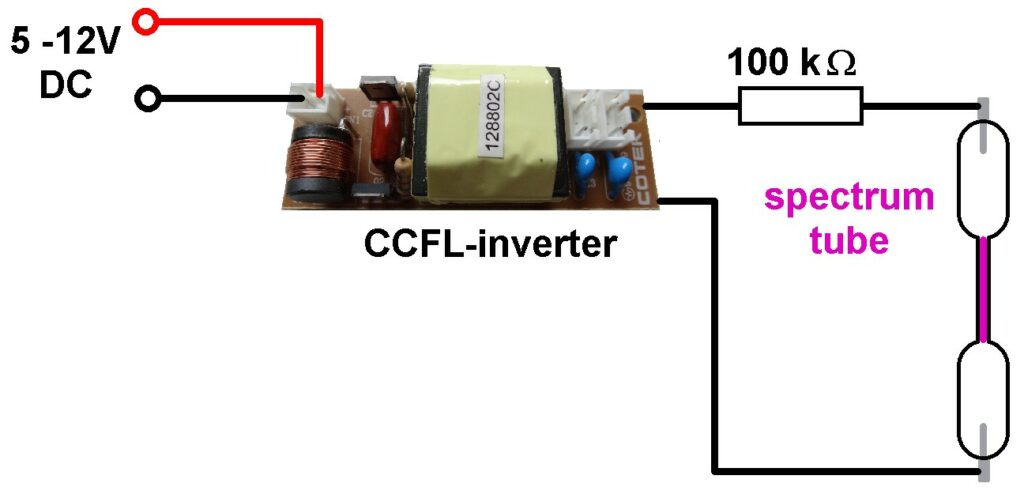

Die Spektralröhre würde ich nur mit einem Vorwiderstand an dem CCFL-Inverter betreiben. Ohne Vorwiderstand zieht der CCFL-Inverter nämlich bei ca. 10V bereits 1.5A und es besteht die Gefahr, dass die Spektralröhre durch Überlastung dabei Schaden nimmt. Ich habe den Vorwiderstand einfach als Serienschaltung von 4 Stück 27 kΩ/2W Widerständen realisiert.

Anmerkung: Die Hitzespuren an den Widerständen stammen nicht von diesem Experiment…
Der Vorwiderstand ist nicht nur dafür gut, die Leistung zu drosseln sondern er sorgt auch dafür, dass zu Beginn eine höhere Zündspannung an der Spektralröhre anliegt, die dann im Betrieb durch den Spannungsabfall am Widerstand sinkt (sog. Brennspannung).
Das Spektrum kann man etwa durch ein einfaches Beugungsgitter mit z.B. 1000 Linien/mm betrachten. Diese Beugungsgitterfolien erhält man um ca. 10 Euro auf ebay.com.

Man kann sich aber auch gleich ein einfaches Spektroskop mit Wellenlängenskala basteln. Empfehlen kann ich jenes von AstroMedia (https://astromedia.de/Das-Handspektroskop). Dieses bekommt man dort sehr günstig um ca. 15 Euro inkl. Versand.



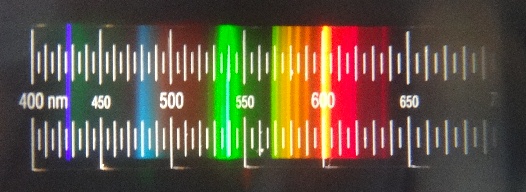
Hier das Spektrum einer Energiesparlampe:

Die Wasserstoff-Spektralröhre ist heute angekommen. Anders als bei typischen Spektralröhren besitzt diese keine inneren Elektroden. Daher müssen sie außen zum Beispiel mittels Draht oder Blech erst angebracht werden. Zum Betrieb ist daher eine AC HV-Quelle notwendig.

Die Gasentladung habe ich dann durch ein Beugungsgitter fotografiert. Sie ist ziemlich lichtschwach und dick, wodurch ich keine schönen, scharfen Linien erhalte. Eigenartigerweise sehe ich im Spektrum auch Grünanteile, die ja so im Wasserstoffspektrum gar nicht vorkommen sollten. Vielleicht ist es auch nur aufgrund der Überlagerung der blauen und roten Linie. Verunreinigungen im Gas sollten es ja eigentlich nicht sein…


Um ein schärferes Spektrum zu erhalten, habe ich die Spektralröhre bis auf einen dünnen Schlitz mit Klebeband eingehüllt. Die Aufnahme erfolgt dann im total dunklen Raum mit einer langen Belichtungszeit (so um die 5 Sekunden).

Heute konnte ich eine erste Aufnahmenserie bei einer Spannung von ca. 1–3 kV mit verschiedenen Beugungsgittern (1000 Linien/mm, 300 Linien/mm und 50 Linien/mm) machen. Ich erhalte aber nach wie vor kein schönes Balmer-Spektrum, sondern extrem viele andere Farbanteile (Banden). Den Grund kenne ich im Moment noch nicht. Es gibt aber im Lehrmittelhandel nicht nur Wasserstoff-Spektralröhren, sondern dezidierte „Balmer-Spektralröhren“. Diese beinhalten eine geringe Menge Wasserdampf zur Reduzierung der Banden! Es scheint also, dass man mit einer gewöhnlichen H2-Spektralröhre, wie ich sie habe, kein schönes Balmer-Spektrum erzielen kann.






Was die störenden Linien/Banden betrifft, bin ich hier auf einen interessanten Vermerk gestoßen:

Hier noch eine Gegenüberstellung meines Spektrums mit einem reinen Balmerspektrum. Es ist sehr schwierig eine Übereinstimmung entdecken zu können, denn die störenden Banden sind in meinen Spektren leider sehr dominant.

Da ich mit meiner ersten Wasserstoff-Spektralröhre keine zufriedenstellenden Ergebnisse erzielen konnte, habe ich mir nun eine solche spezielle „Balmer-Röhre“ gekauft. Gekostet hat mich dieser Spaß rund 65 Euro inkl. Versand und MwSt.
Die Balmer-Spektralröhre ist heute wohlbehalten angekommen. Anders als gewöhnliche Spektralröhren besitzt diese hier noch seitlich ein Reservoire, gefüllt mit einem silbrig glänzenden Pulver (siehe Abbildung unten). Dabei handelt es sich laut Internet um ein Adsorptionsmittel.



Ich konnte/musste heute auch gleich einen Schnelltest machen. Direkt an einem CCFL-Inverter bei 12V und immerhin 1.5A betrieben wird die Röhre sehr hell und leuchtet in einem wunderschönen Purpur. Leider gibt das die Kamera nicht wieder. In diesem Modus ohne Vorwiderstand betreibe ich sie natürlich nur ganz kurz. Und im Gegensatz zu meiner ersten Wasserstoffspektralröhre sehe ich bei dieser sehr deutlich die Balmerlinien 🙂



Insgesamt sind die ersten 3 Linien der Balmerserie, also Hα, Hβ und Hγ gut zu sehen. Ob ich eventuell noch Hδ herauskitzeln kann wird sich zeigen. Visuell sind die Linien ebenfalls deutlicher zu erkennen als auf den Photos.
Hier noch ein aktuelles Photo der Entladung aufgenommen mit meinem Smartphone (Huawei P10 lite). Dieses ist scheinbar deutlich sensibler im roten Spektralbereich als meine Digitalkamera (Sony DSC-HX20V). Man erkennt auch schön die Schichtentladungen nahe den Elektroden.

Habe ich schon gesagt, dass ich Gasentladungen liebe 😉
Heute konnte ich die Spektrallinien der Balmerserie mit Hilfe der Software Tracker (https://physlets.org/tracker/) auswerten.
Zuvor musste ich aber das Beugungsgitter (angegeben waren 300 Linien/mm) mittels grünen DPSS-Laser (λ = 532 nm) eichen. Ich kam auf 315 Linien/mm, was einer Gitterkonstante d = 1000000/315 nm entspricht. Der Aufbau des Experiments sieht folgendermaßen aus:





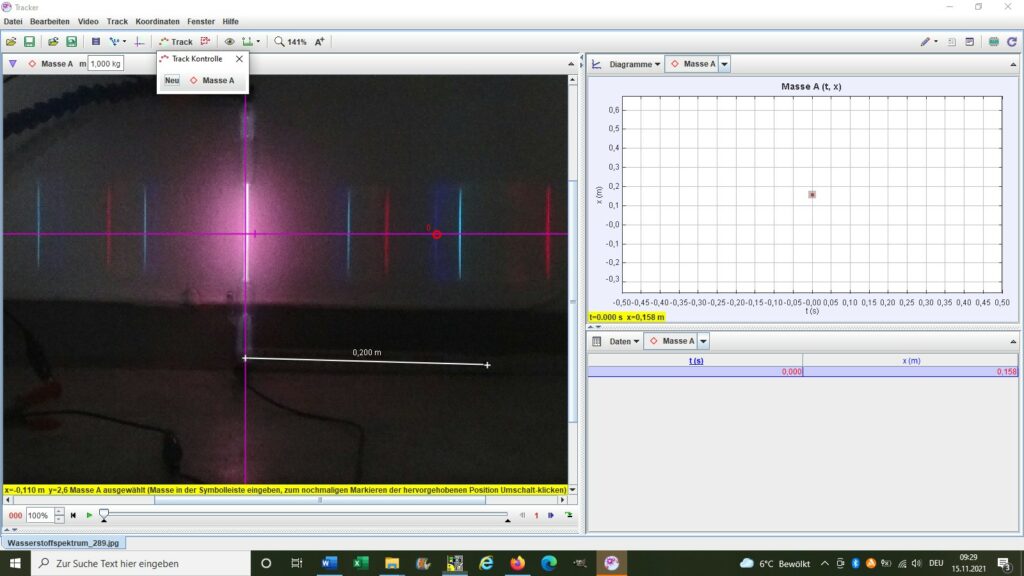
Die Ergebnisse für die experimentell ermittelten Wellenlängen der Balmer-Serie:

Hier nochmals die Sollwerte:

Zwischen der inversen Wellenlänge der Balmer-Serie und der Hauptquantenzahl n besteht folgender einfache Zusammenhang:
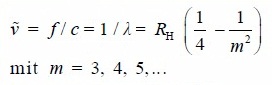
RH ist die sogenannte Rydberg-Konstante. Trägt man also die inversen Wellenlängen 1/λ der Balmerserie gegen 1/m² auf, so müsste man eine abfallende Gerade mit der Steigung k = –RH erhalten. Die Hα-Linie hat dabei die Zählvariable m = 3, Hβ entspricht m = 4 usw.

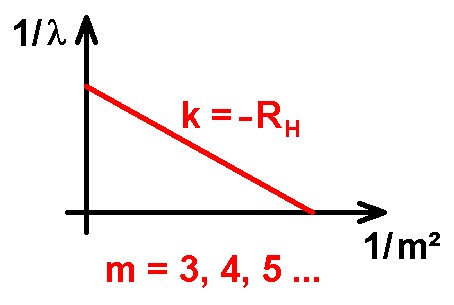
Dies habe ich mit meinen experimentell ermittelten Wellenlängen gemacht:

Die auf diese Weise bestimmte Rydbergkonstante beträgt 1.1 · 10^ 7 1/m und liegt daher sehr nahe am Sollwert:

Quelle: Wikipedia
Zum Abschluss noch das Youtube-Video:

