Hier (https://stoppi-homemade-physics.de/magnetische-feldkonstante/) habe ich die magnetische Feldkonstante μ0 experimentell ermittelt. Sie verknüpft die magnetische Feldstärke H mit der magnetischen Flussdichte B. Das Pendant dazu für die Elektrostatik ist die elektrische Feldkonstante ε0. Sie verknüpft die elektrische Feldstärke E mit der Verschiebungsdichte D, denn es gilt D = ε0 · εr · E bzw. im Vakuum (εr = 1) dann D = ε0 · E. Die elektrische Feldkonstante kommt etwa auch im Coulombgesetz zwischen zwei Ladungen vor. Es lautet:

Ich werde die elektrische Feldkonstante mittels der verschiedenen Beziehungen eines Plattenkondensators experimentell ermitteln und zwar auf 3 Arten.
Variante 1: Kapazität eines Plattenkondensators
Das Speichervermögen von elektrischen Ladungen eines Kondensators wird durch die Kenngröße Kapazität C ausgedrückt. Ein großes C bedeutet, dass ein Kondensator bei einer gleichen Spannung U mehr Ladung Q speichern kann als ein Kondensator mit einer geringen Kapazität. Ein Plattenkondensator ist charakterisiert durch seine Fläche A und den Plattenabstand d. Jetzt kann man sich schon denken, dass die Kapazität mit zunehmender Fläche A steigt und mit zunehmenden Abstand d sinkt. Und genauso ist es…

In Luft (εr ≈ 1) gilt für die Kapazität eines Plattenkondensators C = ε0 · A / d. Kennt man die Fläche A und den Abstand d und ermittelt etwa mit einem Messgerät die Kapazität C, so kann man die elektrische Feldkonstante ε0 bestimmen. Genauso mache ich das auch…
Auf Aliexpress habe ich mir eine 2 mm starke Aluminiumplatte und Plastikschrauben samt Muttern und Beilagscheiben besorgt:




Die Platte habe ich dann in zwei 12 cm x 12 cm große Stücke halbiert.

Mittels der Plastikbeilagscheiben stelle ich einen definierten Plattenabstand d ein. 4 solcher Beilagscheiben besitzen eine Dicke von 3.2 mm, demnach ist eine einzelne Beilagscheibe 0.8 mm dick.


Als Messgerät verwende ich einen sehr günstigen Komponententester. Diesen bekommt man schon für 10 Euro im Internet und ich möchte meinen nicht mehr missen. Man kann mit ihm u.a. Kapazitäten, Induktivitäten und Bauteile (Dioden, Transistoren, Mosfets usw.) bestimmen, einfach genial.

Bei Verwendung von 3 Beilagscheiben zwischen den beiden Kondensatorplatten ermittelt der Komponententester eine Kapazität von C = 66 pF:


Bei Reduzierung auf nur noch 2 Beilagscheiben steigt die Kapazität auf C = 96 pF an:


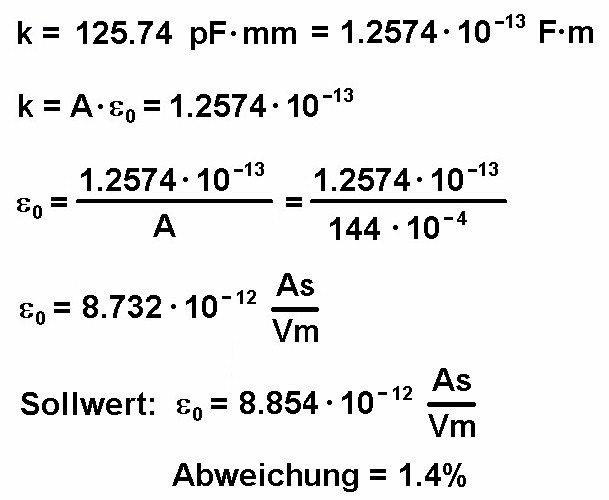
Trägt man die ermittelte Kapazität C gegen den reziproken Abstand, also 1/d auf, so erhält man eine steigende Gerade. Der Anstieg k dieser Geraden ist gleich ε0 · A. Konkret beträgt die Fläche meines Plattenkondensators A = 12 · 12 = 144 cm². Diesen Wert setze ich dann ein:

Hier zum Schluss die Rechnung zur Bestimmung der elektrischen Feldkonstante ε0. Mein experimentelles Ergebnis liegt nur 1.4% vom Sollwert entfernt, Heureka 🙂
Variante 2: Ladung eines Plattenkondensators
Für dieses Experiment benötige ich mein Coulombmeter, denn ich bestimme die elektrische Ladung Q des Kondensators in Abhängigkeit von der Ladespannung U. Es gilt der einfache Zusammenhang: Q = C · U.

Hier mein Selbstbau-Coulombmeter:


An den Ausgang des Coulombmeters hängt man ein Voltmeter und misst eine Spannung. 10 mV entsprechen dann einer Ladung von 1 nC.

Als Spannungsquelle dient mein CCFL-Netzteil. Damit kann ich Spannungen zwischen 30 und 1000 V einstellen…

Der gesamte Messaufbau wie immer auf dem Küchenboden 😉


Hier sieht man die Messelektrode des Coulombmeters, wie sie auf der oberen Kondensatorplatte liegt:

Bei einer Ladespannung von 303 V beträgt die elektrische Ladung laut Coulombmeter 20.41 nC:

Bei einer Ladespannung von 353 V erhalte ich eine höhere Ladung Q und zwar 23.78 nC …

Hier sieht man wie ich die obere Kondensatorplatte mit der Kathode des HV-Netzteils verbinde, also negativ auflade. Die Anode (rotes Kabel) berührt indessen die Unterseite des Plattenkondensators:


Trägt man nun die gemessene Ladung Q gegen die Ladespannung U auf, also Q(U), so sollte man eine steigende Gerade erhalten. Im Anstieg k steckt wieder die elektrische Feldkonstante ε0.


Bei diesem Experiment beträgt die Abweichung von ε0 zum Sollwert 27.5%. Eigentlich sollte die Gerade Q(U) ein wenig steiler sein. Meine flacht für höhere Ladespannungen auch ab. Würde ich nur den ersten Teil bis U = ca. 200 V berücksichtigen, läge mein ermittelter Wert für ε0 um einiges näher am Sollwert.
Variante 3: Kraft zwischen den Kondensatorplatten
Zunächst einmal die kurze Herleitung der Kraft zwischen den zwei Kondensatorplatten:


Die Kraft F ist also proportional zu U², der Fläche A und zu 1/d²:
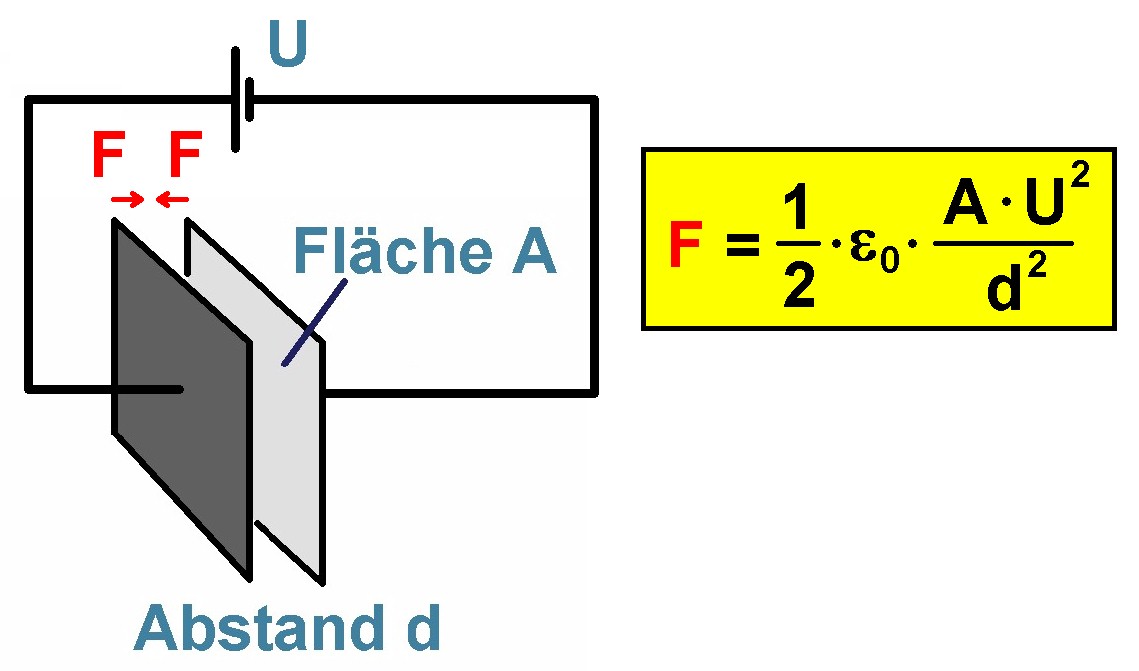
Trage ich F gegenüber U² auf, so müsste ich eine steigende Gerade erhalten, aus deren Anstieg k wieder die elektrische Feldkonstante bestimmt werden kann: 
Zum Einsatz kommt wieder einmal meine Arduino-Waage mit der 100g-Wägezelle. Diese besitzt eine Auflösung von 10 mg, was für dieses Experiment gerade so ausreicht.




Die Anzeige der Kraft in Newton:

„Geladen“ werden die beiden Kondensatorplatten wieder mit meinem CCFL-HV-Netzteil:

Der Abstand d zwischen den beiden Kondensatorplatten bleibt während des Versuchs konstant. Konkret betrug dieser d = 3.76 mm:

Die erhaltenen Messwerte:

Aus dem Anstieg der Geraden F = k · U² kann wie schon erwähnt die elektrische Feldkonstante ε0 ermittelt werden:

Mit der Abweichung von 15.3% gegenüber dem Sollwert bin ich eigentlich sehr zufrieden. Man darf nicht vergessen, dass in die Berechnung von ε0 das Quadrat des Plattenabstands d eingeht und dieser ja trotz der Bemühung die Platten schön parallel auszurichten nicht überall gleich ist…
Variante 4: Coulombgesetz
Hier (https://stoppi-homemade-physics.de/coulombgesetz-coulombmeter/) stelle ich meine Versuche zum Coulombgesetz vor. Es beschreibt die Kraft zwischen zwei Ladungen q und Q im Abstand r:

Die sehr geringe Kraft messe ich mit meiner Arduino-Waage, wobei bei Verwendung einer 100g-Wägezelle die Auflösung 10^ –4 N beträgt.


Der Graph F(1/d²) sollte eine ansteigende Gerade sein:
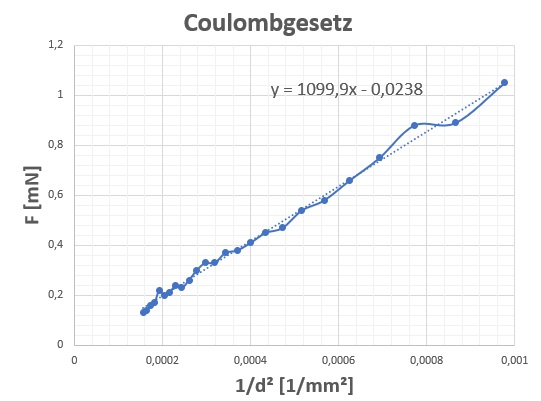
Aus dem Anstieg k kann wieder die elektrische Feldkonstante ermittelt werden:

Bei dieser Messvariante liege ich mit meinem Ergebnis für ε0 ca. bei der Hälfte vom Sollwert. Die gemessenen Kräfte F sind also kleiner als sie sein sollten. Dies kann eventuell dadurch erklärt werden, dass die mit Hochspannung geladenen Kugeln während der Messung an Ladung verlieren und dadurch die Kraft sinkt…

