Erzeugt man mit einer CO2-Patrone zum Beispiel Schlagobers, so macht man folgende Erfahrung: Die CO2-Patrone kühlt dabei ab. Gleiches gilt für Vereisungssprays etwa beim Behandeln von Sportverletzungen. Warum ist dies so?
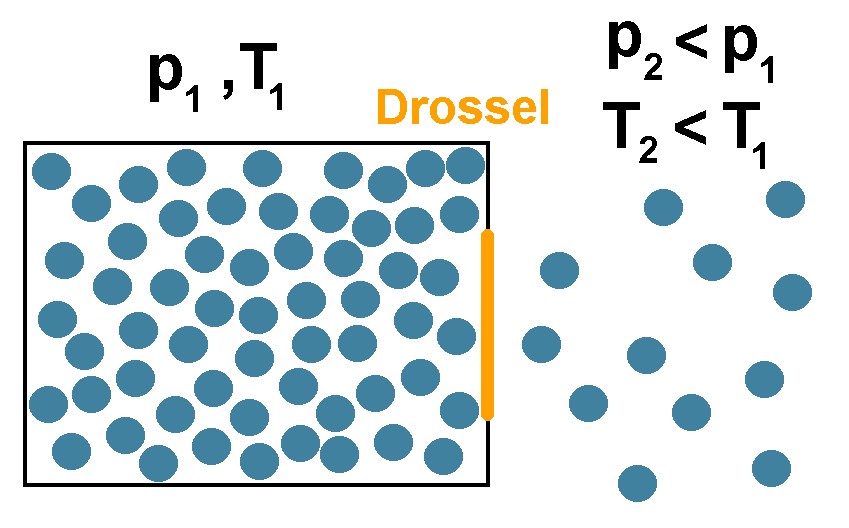
Unter hohem Druck sind die Gasteilchen in der Regel enger beisammen. Entweicht nun der Druck, so strömen die Gasteilchen aus und besitzen sodann einen größeren Abstand voneinander. Für diese zunehmende Entfernung benötigen sie aber Energie, da zwischen den Gasteilchen anziehende Kräfte vorherrschen. Die potentielle Energie der Gasteilchen ist also für größere Abstände höher als im dichtgepackten Zustand.

Woher nehmen die Gasteilchen aber diese Energie für eine zunehmende Entfernung? Sie nehmen diese von ihrer kinetischen Energie (Bewegungsenergie). Entfernen sie sich durch die Druckabnahme voneinander, so werden sie dadurch langsamer. Ähnlich ist es mit einem in die Höhe geworfenen Ball. Auch dessen potentielle Energie nimmt mit der Wurfhöhe zu und seine kinetische Energie nimmt hingegen ab, wenn er an Höhe gewinnt. Langsamere Teilchen bedeuten aber eine geringere Temperatur T. Beim Ausströmen eines unter Druck stehenden Gases nimmt also die potentielle Energie zu, die kinetische Energie ab und demzufolge auch die Temperatur ab.

Diesen Abkühleffekt nennt man Joule-Thomson-Effekt. Der gleichnamige Joule-Thomson-Koeffizient dT/dp gibt an, um wieviel °C die Temperatur pro bar Druckabnahme sinkt. Beispiel für Kohlendioxid:

Dieser Joule-Thomson-Koeffizient wird also durch die Anziehungskräfte der Gasteilchen untereinander bedingt. Deshalb hängt er auch mit den Van-der-Waalskonstanten a und b zusammen. Denn diese berücksichtigen u.a. im Fall von a auch die Kräfte zwischen den Gasteilchen (konkret den real durch die Anziehungskräfte reduzierten Druck) bzw. im Falle von b ihr Volumen.

Ein ideales Gas besitzt ja per Definition kein Volumen (Punktförmigkeit) bzw. es herrschen keinerlei Anziehungskräfte zwischen den Teilchen. Für ein solches ideales Gas gilt daher a = b = 0. Daraus folgt für den Joule-Thomson-Koeffizient eines idealen Gases: µJT,ideales Gas = 0. Ein ideales Gas kühlt also bei Expansion NICHT ab. Reale Gase wie etwa Kohlendioxid mit ihren Anziehungskräften tun dies aber in der Regel schon. Genau um diesen Effekt geht es auch im Experiment.
Betrachtet man die oben angegebenen Werte von µJT für Kohlendioxid genauer, so erkennt man einen Unterschied. Einmal gilt µJT = 1.09 K/bar und dann µJT =0.69 K/bar. Dieser Unterschied rührt daher, da der Joule-Thomson-Koeffizient von der Temperatur T abhängt und dieser in der Literatur für CO2 oft für dessen Sublimationstemperatur T = 194.7 K angegeben wird.

Im Schulmittelhandel gibt es Apperaturen für den Joule-Thomson-Effekt:
Bildquelle: www.phywe.de
Da diese aber nicht gerade günstig sind, habe ich mir ein Alternativexperiment überlegt. Dazu werden lediglich folgende Teile benötigt:
- regulierbare CO2-Patrone für das Aufpumpen von Fahrradschläuchen
- ein digitales Thermometer
Ersteres habe ich auf Amazon bestellt, während ich das Thermometer bereits zuhause hatte.


Der Versuch ist sehr simpel: Man hält den Temperaturfühler vor die Öffnung der CO2-Pumpe und lässt dann schnell den Druck aus dieser entweichen. Sodann bestimmt man mit dem Thermometer die Temperatur des abgekühlten, ausgeströmten Kohlendioxids.
Solche 16 g CO2-Patronen besitzen solange sich noch etwas Flüssigkeit in der Patrone befindet einen Innendruck = Dampfdruck bei 20°C = 57 bar. Der Außendruck beträgt ja 1 bar und damit die Druckdifferenz Δp = –56 bar. Die Temperaturabnahme ΔT wird mit dem Thermometer ermittelt. Daraus folgt dann der Joule-Thomson-Koeffizient µJT = ΔT/Δp.
Kann man mit dem experimentell ermittelten Wert für µJT noch etwas anfangen? Ja und zwar etwas sehr spannendes…
Der Joule-Thomson-Koeffizient hängt wie schon erwähnt mit den Van-der-Waalskonstanten a und b zusammen. b ist das sog. Kovolumen, welches das Volumen von 1 mol Teilchen angibt. Um auf das Volumen eines Gasteilchens zu kommen, muss man lediglich b durch die Avogadro-Konstante NA = 6.023 · 10^ 23 (= 1 mol) dividieren.

Links:
https://de.wikipedia.org/wiki/Joule-Thomson-Effekt
https://www.chemie.de/lexikon/Liste_der_spezifischen_W%C3%A4rmekapazit%C3%A4ten.html
Die Co2-Pumpe ist mittlerweile eingetroffen und so konnte ich das Experiment durchführen:




Die CO2-Patrone selbst kühlt bei dem Versuch natürlich auch stark ab, was die Berechnung des Joule-Thomson-Koeffizienten deutlich erschwert (siehe nachfolgende Betrachtung).

Betrachten wir noch einmal den Joule-Thomson-Koeffizienten µJT:

Beim Versuch entspannt sich das CO2 von einem Startdruck von rund 57 bar (= Dampfdruck bei 20°C) auf 1 bar. Der Innendruck sinkt aber stark während der Expansion. Welchen Wert soll man dann also für Δp einsetzen? Ähnliches gilt für die Temperatur. Zu Beginn des Experiments gilt noch Tinnen = Raumtemperatur = 21 °C. Doch durch den Joule-Thomson-Effekt kühlt natürlich auch das noch in der Patrone befindliche Gas ab. Und mit abnehmender Innentemperatur sinkt auch die Temperatur des entspannten Gases außerhalb der Patrone. Also auch hier ist es alles andere als einfach, die Temperaturabnahme ΔT zu ermitteln. Ich habe mich für mittlere Werte entschieden relativ unmittelbar nach der Expansion. Die Temperatur ist dann natürlich noch weiter gesunken und der Innendruck auch.
Betrachten wir jetzt die zweite Beziehung des Joule-Thomson-Koeffizienten µJT:

Wie man sieht, muss man hier zur Berechnung des Van der Waalsparameters b die Temperatur T und die spezifische Wärmekapazität Cp einsetzen. Cp hängt aber ebenfalls von der Temperatur T ab. Welche Werte setzt man hier also für T bzw. Cp aber ein, wenn doch die Temperatur von 21°C auf –70°C während des Experiments sinkt…
Hier nun „meine“ Rechnung:

Mittels Van der Waals-Parameter b lässt sich dann das Volumen eines CO2-Moleküls ermitteln:
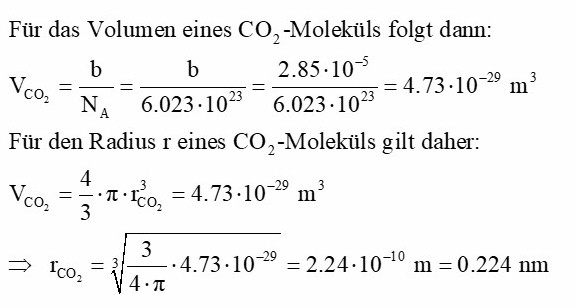
Die Berechnungen wären deutlich eindeutiger, wenn man nur einen geringen Druckabfall von zum Beispiel 1 bar wählen würde. Dann wäre nämlich die Temperaturabnahme ΔT auch nur sehr gering und ich wüsste viel besser, welche Werte ich in die Formeln eintragen müsste. So bleiben sehr viele Fragezeichen. Aber ein schöner Versuch bleibt es trotzdem, mit dem man zumindest auch die Größe eines Moleküls abschätzen kann… 😉

