Der Tunneleffekt ist ein quantenmechanisches Phänomen, welches klassisch nicht zu erklären ist. Nehmen wir zum Beispiel eine Hochschaubahn:
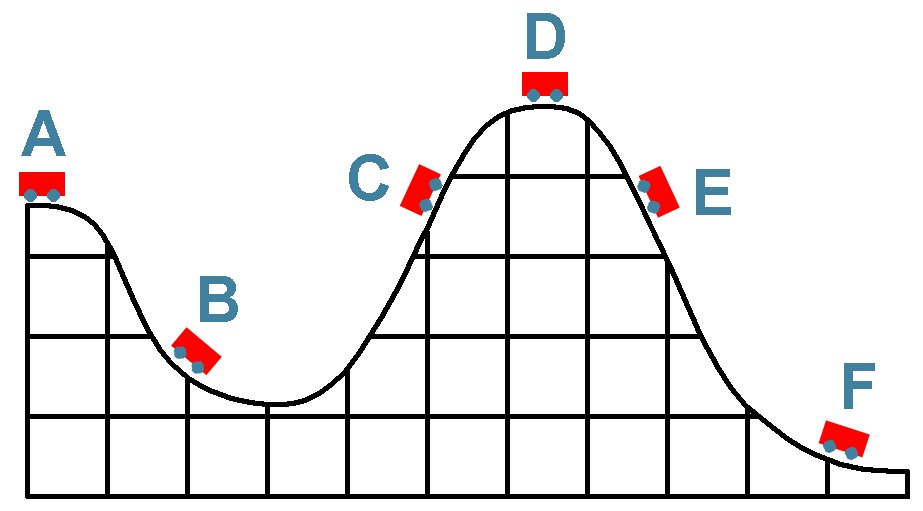
Der Wagen wird am Punkt A losgelassen. Er saust zu Beginn hinab und besitzt am Ort B aufgrund der Reduzierung seiner potentiellen Energie eine hohe kinetische Energie. Am Weg wieder hinauf wird seine kinetische Energie (Geschwindigkeit) nun kleiner, seine potentielle Energie steigt aber wieder. Klassisch betrachtet und ohne Reibung würde der Wagen am Ort C (gleiche Höhe wie Punkt A) zum Stillstand kommen. Er könnte niemals den Punkt D erreichen bzw. den Berg überwinden, da seine Gesamtenergie nicht für die zu hohe potentielle Energie im Punkt D ausreicht. Was passiert aber quantenmechanisch?
Der Wagen kann quantenmechanisch aber durch diese scheinbar unüberwindbare Energiebarriere von C nach E durchtunneln. Am Ort E angekommen nimmt er wieder in Richtung Ort F an Fahrt auf. Der Tunneleffekt erklärt also, wie quantenmechanische Objekte (zum Beispiel Elektronen) energetische Hindernisse überwinden, obwohl die Teilchenenergie eigentlich dazu nicht ausreichen dürfte.
Ausgangspunkt quantenmechanischer Berechnungen ist die sog. Schrödingergleichung. Dabei handelt es sich um eine Differentialgleichung mit der gesuchten Wellenfunktion ψ(r,t) bzw. ψ(r).

Nehmen wir für das Potential V(x) folgende Potentialbarriere 
Klassisch betrachtet könnte ein Teilchen mit der Energie E < V0 diese Potentialbarriere nicht überwinden und sich im Bereich III nach rechts weiter fortbewegen.
Um die Schrödingergleichung zu lösen, setzt man für die Bereiche I und III mit V(x) = 0 folgende Wellenfunktion ψ(x) an:

Setzt man ψ(x) und ψ“(x) in die Schrödingergleichung ein, erhält man folgende Lösungsfunktion für die Bereiche I und III:

Für den Bereich II mit V(x) = V0 setzt man für die Wellenfunktion ψ(x) wiefolgt an:
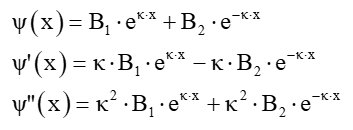
Dies liefert eingesetzt in die Schrödingergleichung folgendes Ergebnis für die Wellenfunktion im Bereich II:

Insgesamt lautet die Wellenfunktion ψ(x) also:


Wie man erkennen kann, nimmt die Wellenfunktion ψ(x) im Bereich II zwar exponentiell ab, sie ist aber am rechten Ende der Potentialbarriere bei x = a nicht vollends verschwunden. Graphisch dargestellt gilt also für die Wellenfunktion folgender Verlauf:
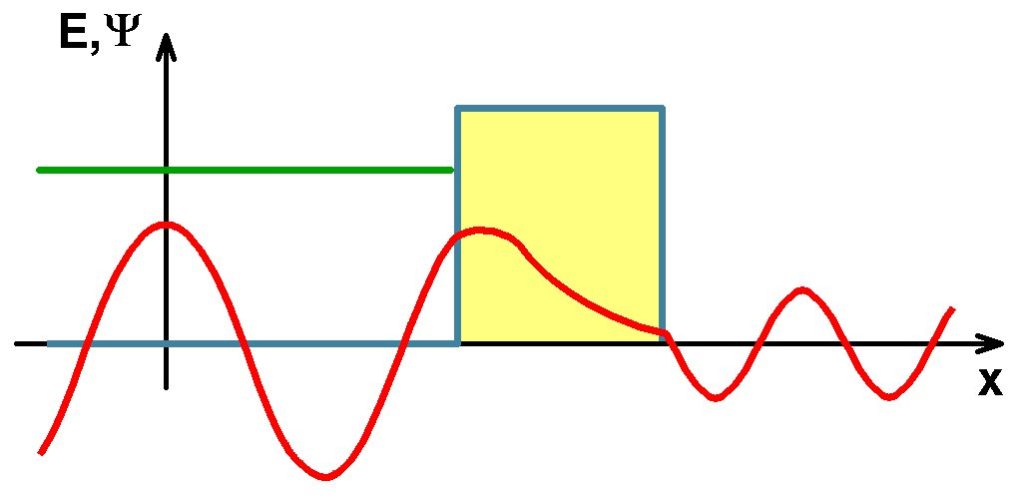
Die Wellenfunktion nimmt zwar im Bereich der Potentialbarriere exponentiell ab, sprich die Aufenthaltswahrscheinlichkeit wird immer geringer, aber ist die Potentialbarriere nicht zu breit, so besteht für das Teilchen eine bestimmte Wahrscheinlichkeit, diese Barriere zu durchtunneln und im Bereich III noch existent/detektierbar zu sein. Für die Tunnelwahrscheinlichkeit T ergibt sich schlussendlich der Ausdruck

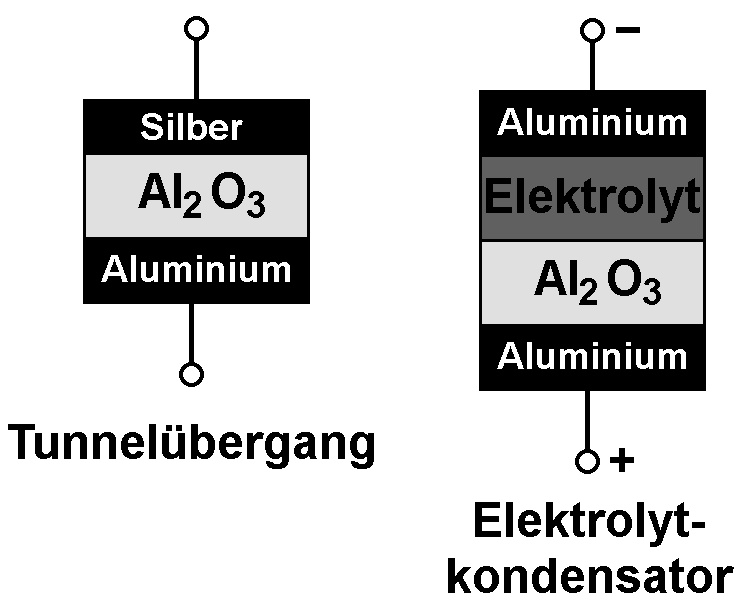
Betrachten wir zunächst einen typischen Tunnelübergang (engl. tunnel junction). Zwei Elektroden aus Metall sind durch einen Isolator bestehend z.B. aus Al2O3 voneinander getrennt. Normalerweise dürfte beim Anlegen einer Spannung durch den Isolator kein Strom fließen. Da aber Elektronen diese Potentialbarriere durchtunneln können, fließt dennoch ein kleiner Leckstrom. Einen dazu ähnlichen Tunnelübergang findet man bei einem Elektrolytkondensator vor (siehe unten rechts).
Betrachten wir den Potentialverlauf V(x) zwischen den beiden Platten eines Kondensators einmal ohne und einmal mit einer angelegten Spannung U:
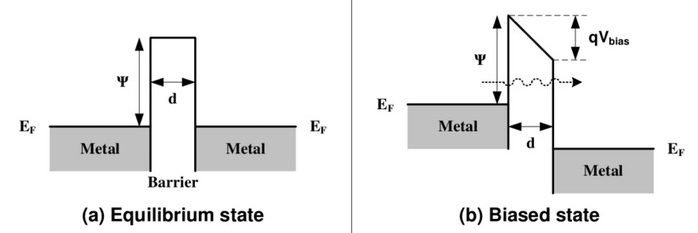
Wie man sieht, wird durch die angelegte Spannung U (in der Abbildung V_bias) der Potentialwall abgeschrägt/niedriger. Dadurch steigen Tunnelwahrscheinlichkeit und Leckstrom. Um den Effekt berechnen zu können, gehen wir zunächst einmal von der Formel zur Berechnung der Tunnelwahrscheinlichkeit für den allgemeinen Fall V(x) aus.

Konkret für einen abgeschrägten Potentialwall müssen wir folgende 2 Fälle unterscheiden.
Fall 1: E < V0 – U·e
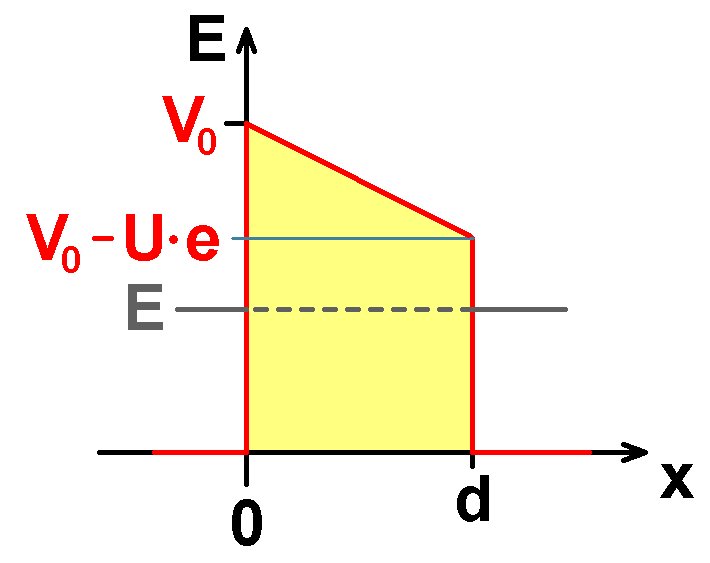
Fall 2: E > V0 – U·e
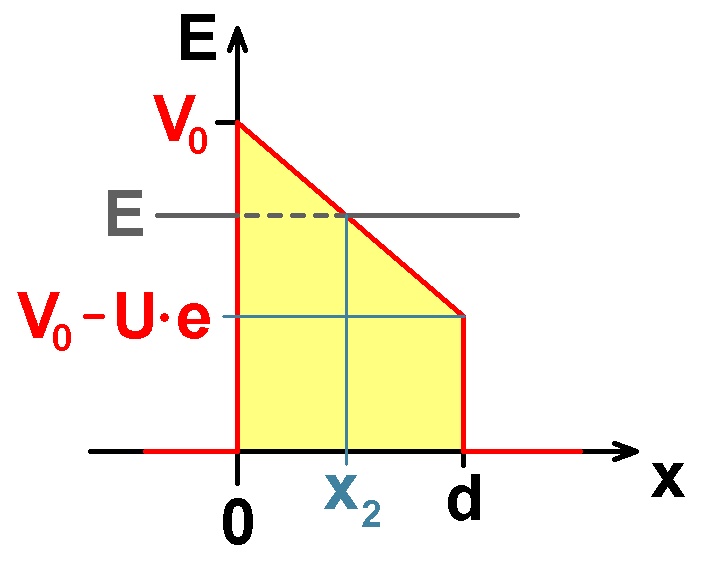
Bei noch geringer Spannung U liegt also Fall 1 und bei steigender Spannung U irgendwann dann Fall 2 vor. Setzt man nun den abgeschrägten Potentialverlauf in das Integral zur Berechnung der Tunnelwahrscheinlichkeit ein, erhält man
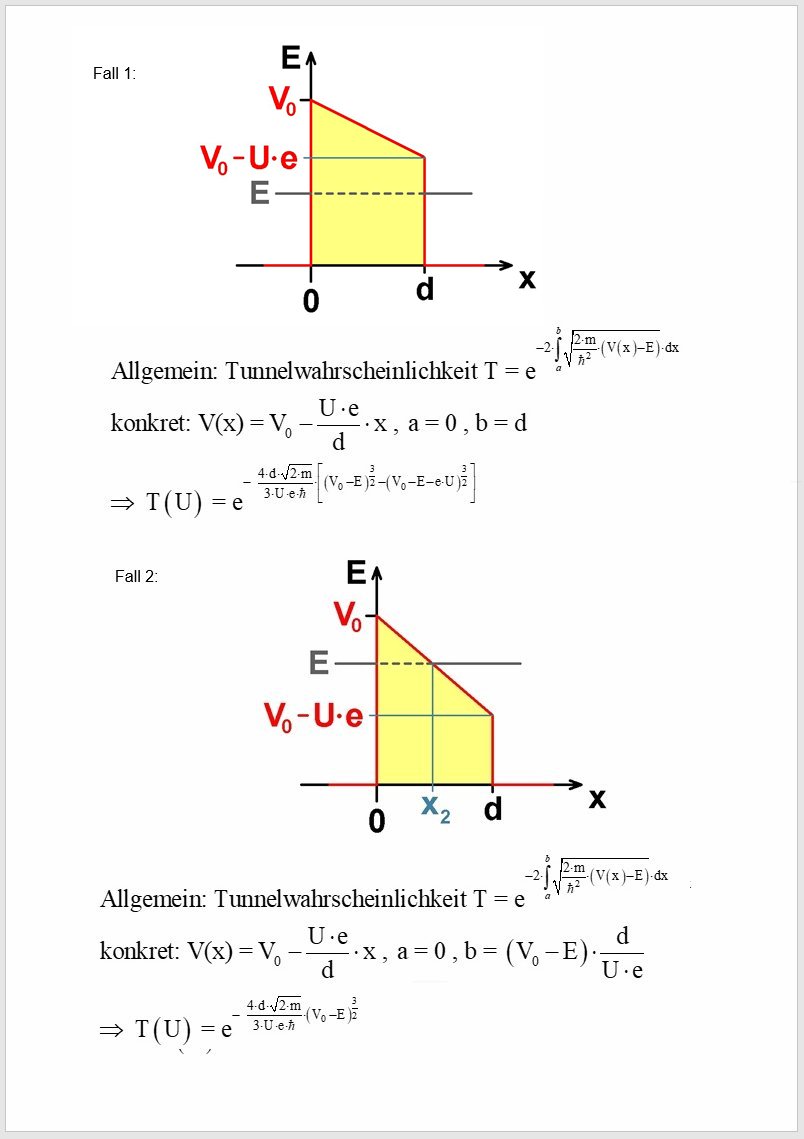
Zeichnet man nun beide Graphen, so ergibt sich folgender Verlauf T(U) für die Tunnelwahrscheinlichkeit in Abhängigkeit von der Spannung U:
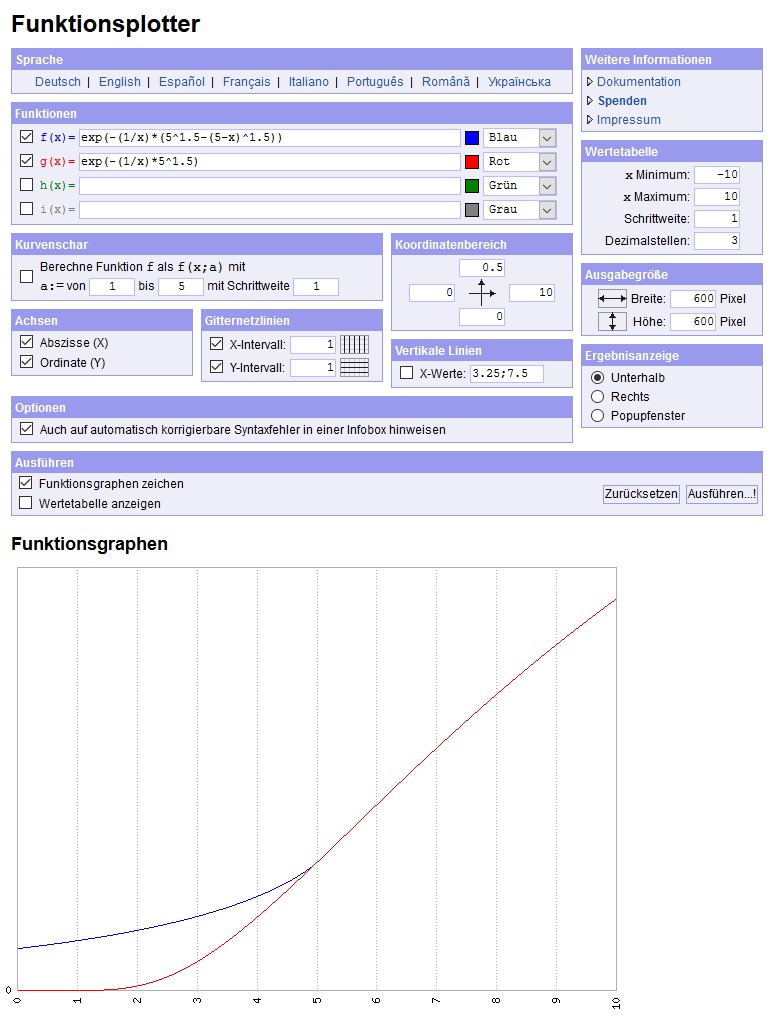
Die blaue Kurve bis zu x = 5 entspricht dem Fall 1, die daran anschließende rote Kurve für x > 5 dem Fall 2. Man erkennt einen nicht linearen Anstieg der Tunnelwahrscheinlichkeit (= Maß für den Leckstrom I) in Abhängigkeit von der Spannung U!
Um anhand der Tunnelwahrscheinlichkeit den Strom zu berechnen, müsste man die Tunnelwahrscheinlichkeit T in einen Widerstand R umrechnen. Bei T = 0 gilt R = ∞ und bei T = 1 müsste der Widerstand verschwinden, R = 0 sein. Dies erzielt man mittels folgender einfachen Beziehung zwischen R und T:
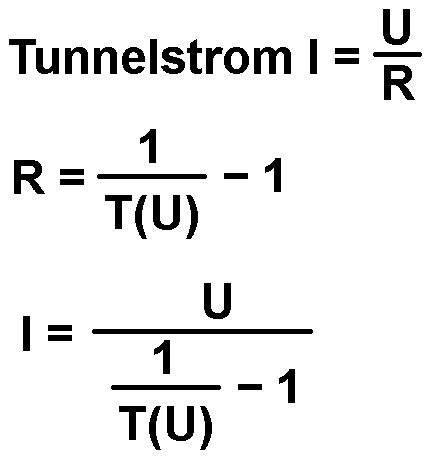
Der Tunneleffekt müsste sich also experimentell mittels eines Elektrolytkondensators nachweisen lassen, indem der Leckstrom I in Abhängigkeit von der angelegten Spannung U bestimmt wird. Der Schaltplan dazu ist mehr als simpel:
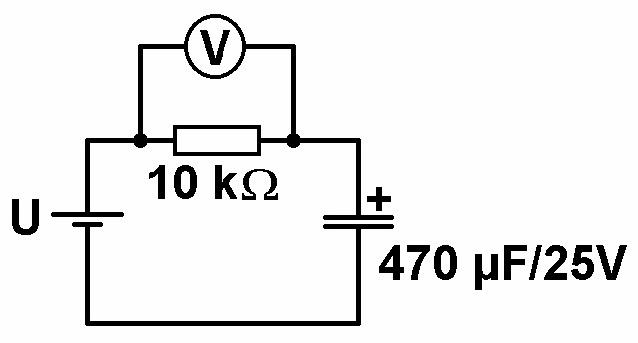
Gemessen wird also die am Widerstand R abfallende Spannung (= proportional zum Leckstrom I) in Abhängigkeit von der Spannung U. Hätte das Dielektrikum zwischen den beiden Platten einen sehr großen ohmschen Widerstand aber eben keinen unendlich großen, so würde man einen linearen Verlauf des Graphen I = I(U) erwarten. Spielt jedoch der Tunneleffekt eine Rolle, so hängt die Tunnelwahrscheinlichkeit wie wir oben gesehen haben exponentiell von der Spannung U ab!


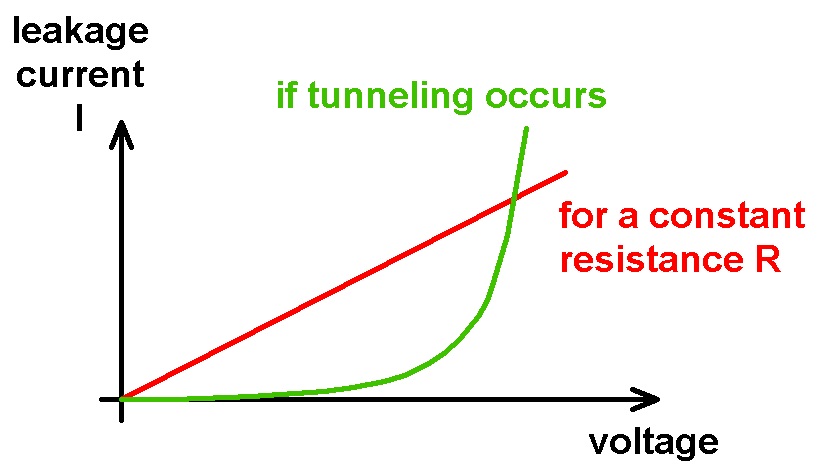
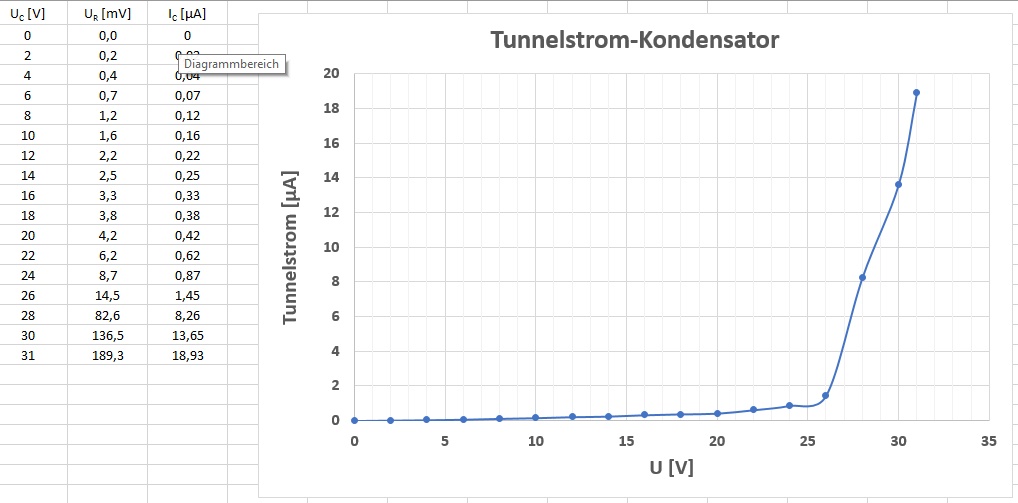
Wie wir anhand des experimentell ermittelten Graphen I = I(U) sehen, erhalten wir keinen linearen Anstieg des Leckstroms sondern einen exponentiellen Verlauf, wie es eigentlich die Theorie vorhersagt.
Tunneldiode
Bei der Tunneldiode kommt es ebenfalls zum Tunneleffekt. Eine Tunneldiode unterscheidet sich im Vergleich zu einer herkömmlichen Diode dadurch, dass sie viel stärker dotiert ist. Dadurch ist die Sperrschicht an der Verbindungsstelle des n- und p-dotierten Bereichs viel schmäler. Die Fermienergie liegt im p-dotierten Bereich im Valenzband und im n-dotierten Bereich im Leitungsband.
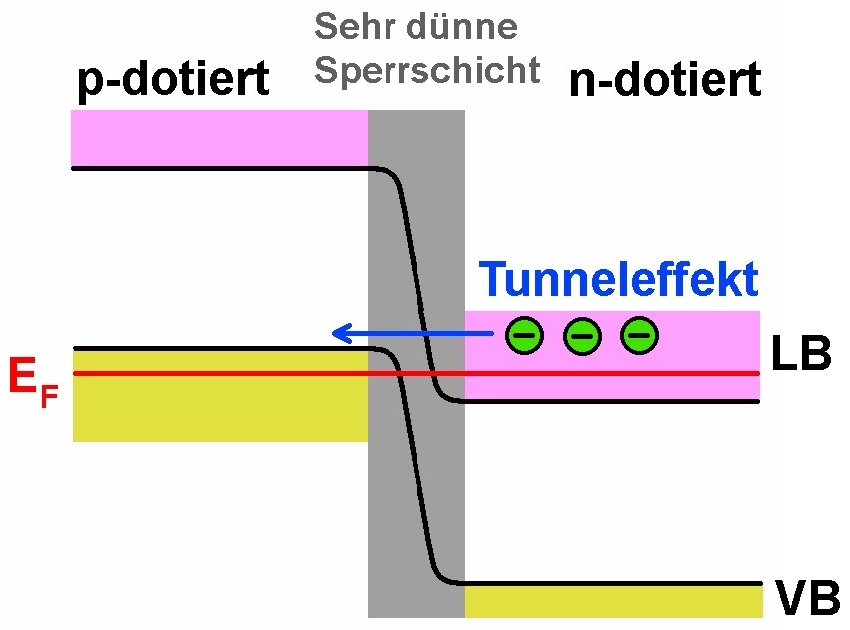
Durch die äußerst dünne Sperrschicht können nun Elektronen selbst bei sehr geringer elektrischer Spannung durch diese tunneln. Die Kennlinie einer Tunneldiode besitzt daher bei sehr geringen Spannungen bereits ein Maximum, den Esakistrom aufgrund des Tunneleffekts.

Tunneldioden werden nur noch selten angeboten. Auf ebay findet man aber zumeist russische Typen wie etwa die 1I308I.
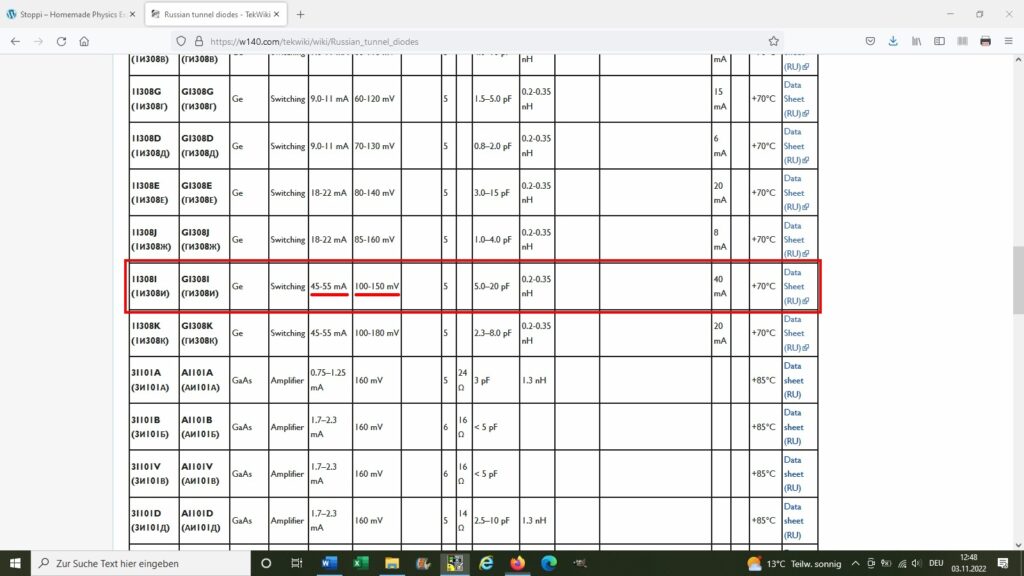
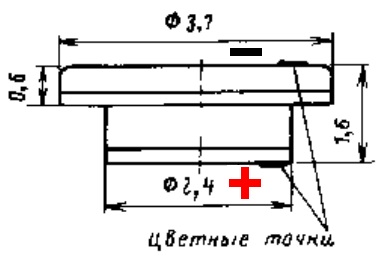
Die Tunneldiode 1I308I ist inzwischen aus Litauen eingetroffen und so konnte ich deren Kennlinie I(U) aufnehmen.


Dieses Experiment zum Tunneleffekt besteht also aus der Aufnahme der Tunneldiodenkennlinie. Hierfür schließe ich die Tunneldiode an ein variables Netzteil mit einer fein einstellbaren Ausgangsspannung zwischen 0 V und ca. 0.5 V und messen jeweils die U/I-Werte. Dabei wird man feststellen, dass die Kennlinie im Bereich des negativen differentiellen Widerstands nur schwer aufzunehmen ist. Die Spannung springt hier und lässt sich nicht schön kontinuierlich erhöhen!
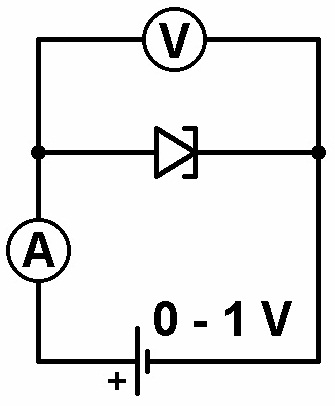



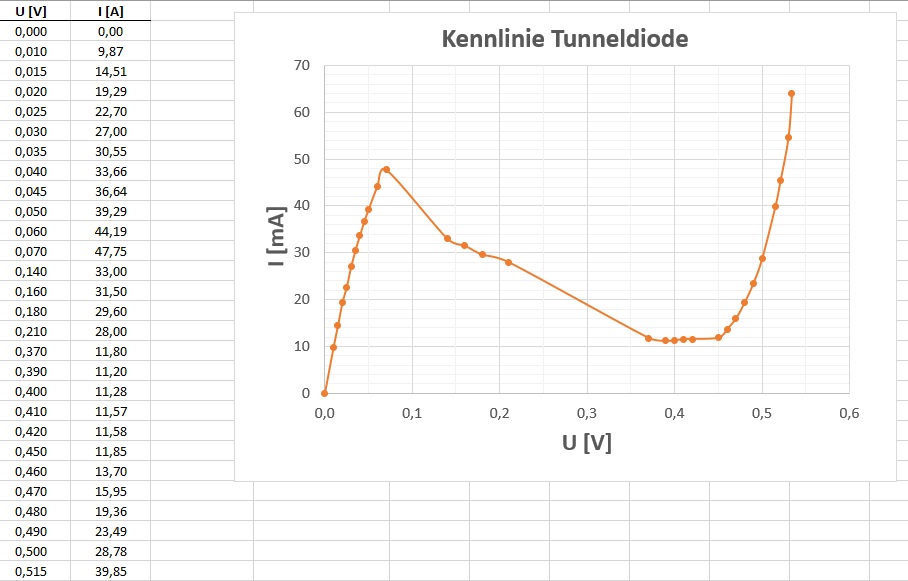
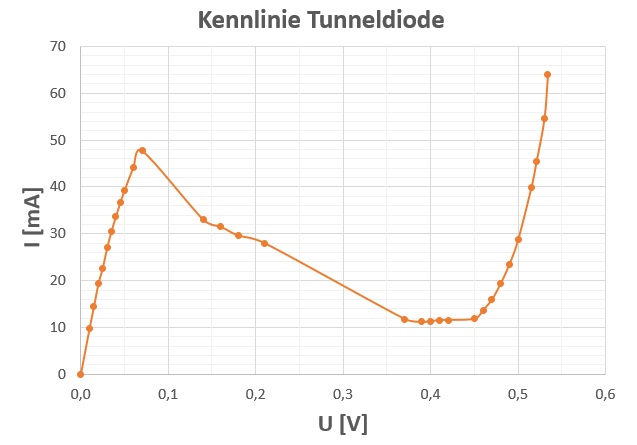
Man erkennt aber eindeutig die für Tunneldioden typische Kennlinie mit einem Maximum bei sehr geringer Spannung. 😉
Quantum tunneling Composites – QTC
Bei den quantum tunneling composites handelt es sich um ein Material, dessen Widerstand von der mechanischen Belastung abhängt. Quantentunnelverbundwerkstoffe sind Verbundwerkstoffe aus einem nicht leitenden elastomeren Bindemittel, in das kleinste Metallpartikel zumeist aus Nickel eingelagert sind. Ohne Druck ist der mittlere Abstand zwischen den einzelnen Metallpartikel groß und demnach die Tunnelwahrscheinlichkeit bzw. die elektrische Leitfähigkeit gering. Unter Druck reduzieren sich die Abstände und die Tunnelwahrscheinlichkeit bzw. die Leitfähigkeit steigt stark an.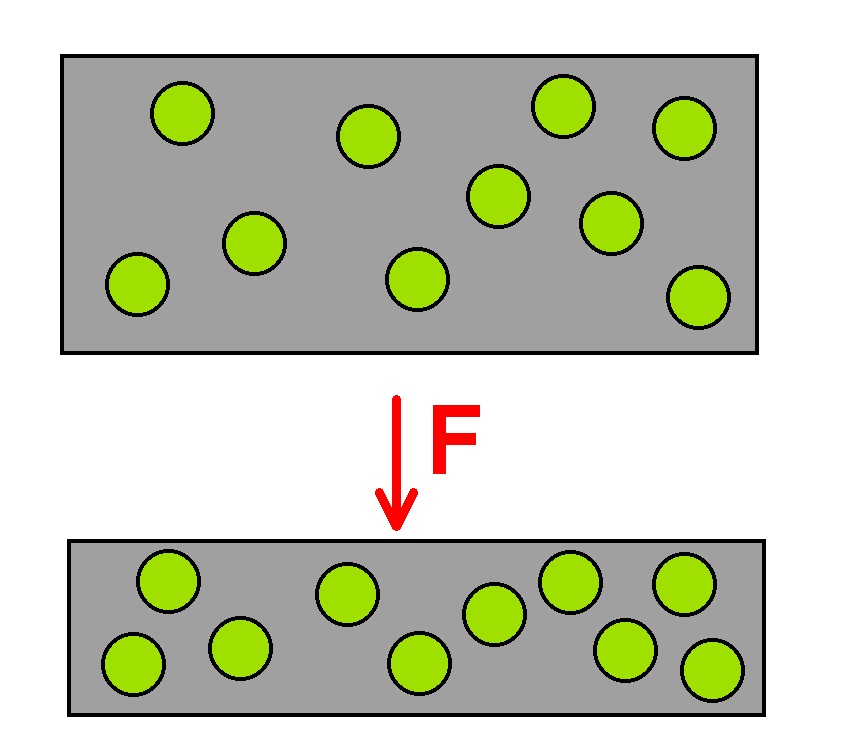
Als einfaches Modell dafür eignet sich eine Potentialbarriere der Breite 2·a. Für diese gilt:


Leider gibt es (Stand 2022) fast keine Möglichkeit mehr, dieses Tunnel-Material online zu kaufen. Vor 10 Jahren war dies noch anders. Hier ein Link zu einem damaligen Verkaufsangebot: https://www.tindie.com/products/VersaRobotics/quantum-tunneling-composites/
In dem Buch „Low Cost – High Tech Freihandversuche Physik“ (https://www.think-ing.de/materialien/low-cost-high-tech-freihandversuche-physik) ist ein einfacher Versuch zum Thema QTC beschrieben. Mit einer Mikrometerschraube komprimiert man das Material und reduziert dadurch seinen Widerstand R. Es müsste sich im halblogarithmischen Diagramm log(R) in Abhängigkeit von der Kompression eine Gerade ergeben.

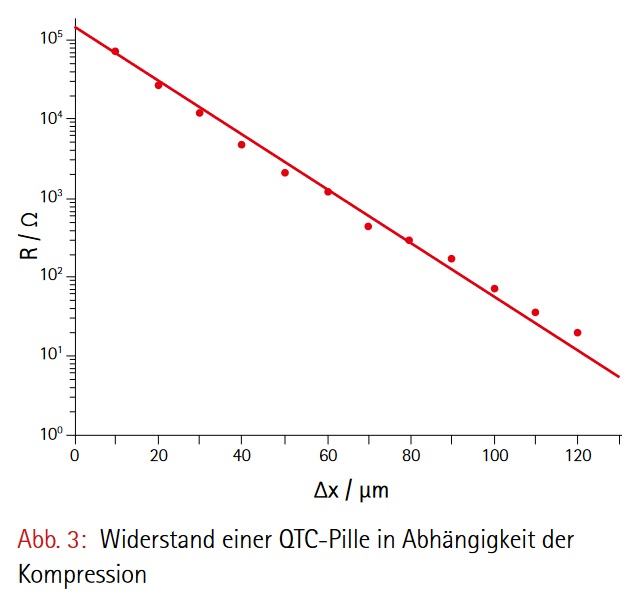
Quelle beider Bilder: https://www.think-ing.de/materialien/low-cost-high-tech-freihandversuche-physik
Im Internet bin ich auch auf das Material Velostat / Linqstat gestoßen. Auch dieses verändert bei Druck seinen elektrischen Widerstand. Habe mir deshalb gleich einmal eine Probe bestellt:
Leider handelt es sich nicht um ein QTC und es spielen daher keine quantenmechanischen Effekte eine Rolle. Ein netter Versuch ist es aber trotzdem. Ich habe einen Stapel bestehend aus rund 15 Quadraten gebildet und dann dessen Widerstand in Abhängigkeit vom Druck beobachtet. Die Werte reichen von 60 kΩ ohne Druck bis unter 1 kΩ mit Druck:





Wenn ich ein orginal QTC-Material besorgt habe geht es hier weiter…

