Beim schiefen Wurf geht es um die Bestimmung der Flugbahn eines Objekts, welches unter einem bestimmten Winkel α mit der Geschwindigkeit v auf der Erde abgeschossen wird. Es unterliegt also der Schwerkraft und Reibungskräften wie Luftwiderstand. Ohne Luftwiderstand ergeben sich Wurfparabeln. Diese können sehr einfach mit Excel simuliert werden:

Es gelten folgende Gleichungen:
vx = v · cos(α)
vy = v · sin(α)
x(t) = vx · t
y(t) = vy · t – 1/2 · g · t²

Excel-Datei: Excel_Wurf_ohne_Reibung
Die Beziehung für die Reichweite w(α) in Abhängigkeit vom Abschusswinkel lautet: w = 2 · v² · sin(α) · cos(α) / g. Die maximale Reichweite wmax ergibt sich ohne Reibung bei einem Abschusswinkel von α = 45°, denn dann ist der Ausdruck sin(α) · cos(α) maximal. Es gilt dann: wmax = v² / g.
Die Verhältnisse bei Berücksichtigung des Luftwiderstands sind um einiges komplexer, aber auch dieser Fall lässt sich noch relativ leicht mit Excel simulieren:
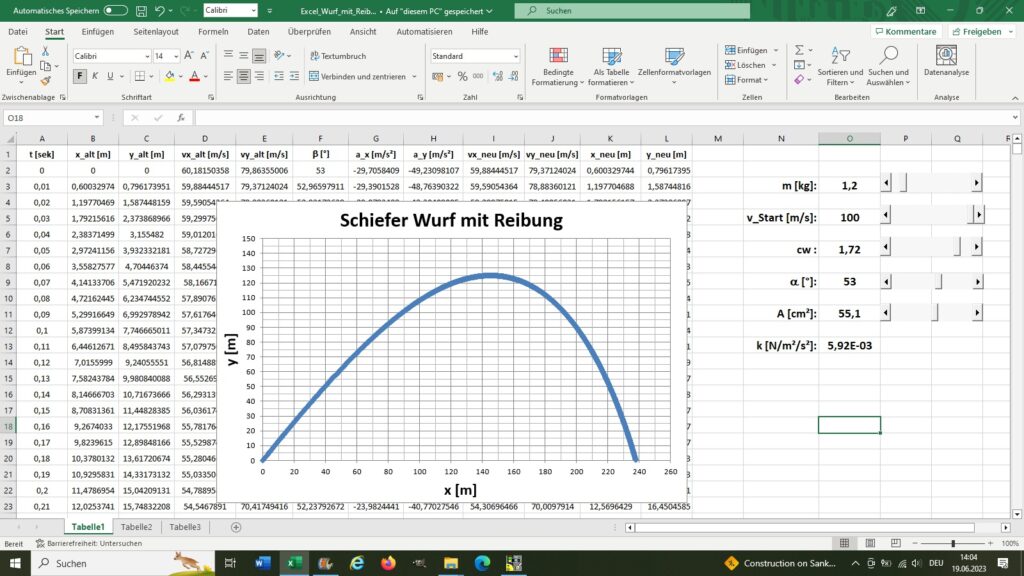
Excel-Datei: Excel_Wurf_mit_Reibung
Für den Luftwiderstand wurde folgende Formel verwendet: FLuftwiderstand = 1/2 · ρ · cw · A · v². Diese muss aber selbstverständlich vektoriell berücksichtigt werden, indem sie mit dem Einheitsvektor Vektor v / Betrag v noch ergänzt wird. Mit Luftwiderstand wird nun die maximale Schussweite nicht mehr bei α = 45° erzielt, sondern bei einem flacheren Winkel.
Die Differentialgleichung wird iterativ mittels Euler-Verfahren gelöst. Dabei wird mit den aktuellen Geschwindigkeitskomponenten vx und vy zunächst der Luftwiderstand ausgerechnet und dann die wirkenden Beschleunigungen ax und ay mittels der Newtonschen Bewegungsgleichung F = m · a bzw. a = F / m. Für die neue Geschwindigkeit v(t + Δt) gilt dann: v(t + Δt) = v(t) + a · Δt. Den neuen Ort s(t + Δt) erhält man mittels der Beziehung: s(t + Δt) = s(t) + 1/2 · [v(t) + v(t + Δt)] · Δt. Wählt man die Zeitschrittweite Δt klein genug, erzielt man mit diesem Verfahren ausreichend genaue Ergebnisse. Auf diese Weise lassen sich auch komplexere Bewegungen einfach und nachvollziehbar simulieren.

Zu jedem meiner Projekte gehört natürlich immer auch ein Experiment. Der schiefe Wurf lässt sich sehr anschaulich mittels LEGO-Teilen bzw. einer Trinkhalmrakete durchführen.
Für die LEGO-Variante benötigt man nur wenige Teile, sodass sich dieser Versuch sehr gut für das Physiklabor in der Schule eignet. Hier die Teileliste:

Herzstück ist der sog. Projectile launcher/spring shooter, den man auf Bricklink bereits für kleines Geld bekommt. Die dazu passenden Pfeile/Projektile können ebenfalls auf Bricklink für wenige Cent das Stück erworben werden. Den Abschusswinkel stellt man manuell mit einer sog. Hinge Plate 2 x 4 ein. Ich habe gleich 19 Stück davon besorgt, damit fast jeder Schüler seinen eigenen “Schussapparat” besitzt.
Aufgabe ist es, die Schussweite w in Abhängigkeit vom Abschusswinkel α zu ermitteln. Dazu wird der Versuch für jeden Abschusswinkel zum Beispiel 3mal wiederholt und dann der Mittelwert aus den 3 Weiten bestimmt. Trägt man diesen Mittelwert in Abhängigkeit vom Abschusswinkel in einen Graph, müsste man eine Kurve mit einem Maximum bei ca. 30-40° erhalten…
Die über Bricklink bestellten Legoteile konnte ich inzwischen direkt beim Verkäufer vor Ort abholen, völlig unkompliziert und zudem noch ohne zusätzliche Portokosten.

Die “Kanonen” waren schnell aufgebaut. Von der Schussweite war ich ehrlich gestanden positiv überrascht. Die weitesten Schüsse gehen schon an die 2.5 m.



Für das Experiment habe ich verschiedene Abschusswinkel eingestellt und dann jeweils die Schussweite ermittelt. Dies funktioniert nicht immer gut und die Pfeile haben doch des öfteren bei gleichen Bedingungen unterschiedliche Geschwindigkeiten. Deshalb muss man den Versuch für jeden Abschusswinkel öfters wiederholen und dann entweder für jedes α den Mittelwert bilden oder die maximale Schussweite nehmen. Hier meine Ergebnisse:

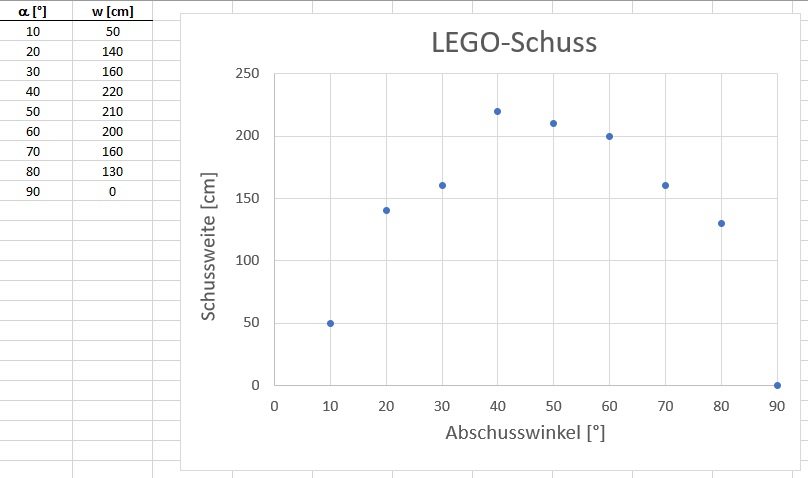
Entgegen der Theorie erhalte ich fast bei Abschusswinkel knapp größer als 45° weitere Schüsse. Dies experimentell zu überprüfen überlasse ich aber meinen Schülern im Physiklabor…
Die LEGO-Pfeile eignen sich sehr gut für den Physiksaal, da die Schusskraft nicht sehr groß ist. Bei der Trinkhalmrakete ist dies anders. Mit dieser lassen sich Flugweiten von 20 m und mehr erzielen. Man benötigt nur wenige Teile und zwar
- eine Fahrradhandpumpe
- ein Messingrohr, welches gut in die Pumpenöffnung passt und vom dort befindlichen Gummi abgedichtet wird
- dickere Trinkhalme, z.B. jene von Mc Donalds
- Papier für die Leitwerke
- Knetmasse



Die Leitwerke werden an einem Ende des Trinkhalms angeklebt. Am anderen/oberen Ende stopft man ein wenig Knetmasse in den Halm. Dann steckt man das Messingrohr in die Pumpe und stülpt die Rakete über das Messingrohr. Mit Druck wird dann das Rohr in die Knetmasse gedrückt, sodass diese abdichtet. Drückt man nun die Pumpe schnell zusammen, baut sich ein Innendruck auf, bis sich die Knete mitsamt der Rakete vom Messingrohr löst und davonsaust. Damit der Trinkhalm dabei nicht aufgerissen wird, kann er am Ort der Knetmasse mit etwas Klebeband verstärkt werden (siehe Abbildungen).
Die Trinkhalmrakete wird von den Schülern im Freien wieder unter verschiedenen Abschusswinkeln abgeschossen und jeweils die Flugweiten notiert und in einen Graphen eingetragen. Danach zeichnen sie die Ausgleichskurve und bestimmen die Lage des Maximums, sprich den optimalen Abschusswinkel für die maximale Flugweite:


