Mit einem Kugelfallviskosimeter lässt sich die Viskosität η einer Flüssigkeit bestimmen. Die Viskosität η ist ein Maß für die inneren Reibungskräfte einer Flüssigkeit, wenn diese in Bewegung gesetzt wird. Viskosität wird umgangsprachlich auch als Zähigkeit bezeichnet. Die definierende Formel lautet: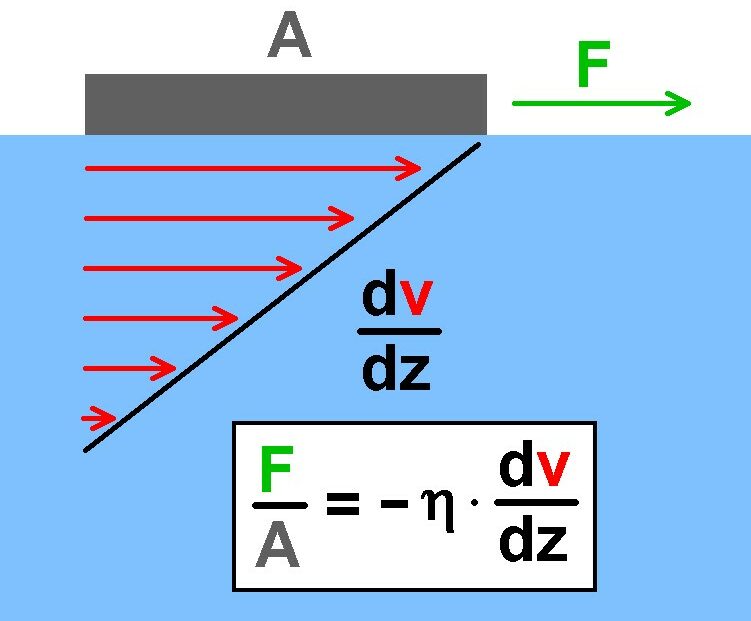

Wird eine Platte mit der Fläche A auf der Oberfläche einer Flüssigkeit verschoben, so ist hierfür aufgrund der Reibung/Viskosität eine bestimmte Kraft F notwendig. Je zäher die Flüssigkeit, desto größer ist natürlich diese Kraft. In der Formel kommt noch die Geschwindigkeitsabnahme dv/dz der einzelnen Flüssigkeitsschichten vor und eben die Viskosität η. Deren Einheit ist N·s/m² oder auch Pa·s.

Hier eine Tabelle mit einigen Viskositätswerten:

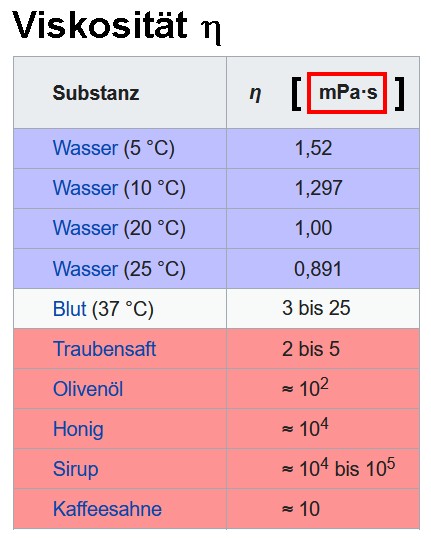
Quelle: https://de.wikipedia.org/wiki/Viskosität

Wie man sieht, kann die Viskosität η um viele Zehnerpotenzen differieren. Für Wasser beträgt sie rund 0.001 Pa·s, für Honig beachtliche 10 Pa·s, immerhin das 10000-fache.

Wie kann man nun die Viskosität η einer Flüssigkeit experimentell bestimmen? Ich verwende hierfür ein sog. Kugelfallviskosimeter. Dieses besteht eigentlich nur aus einer mit der zu untersuchenden Flüssigkeit gefüllten Röhre und einer Metallkugel (Radius r_Kugel, Masse m_Kugel). Die in der Flüssigkeit sinkende Kugel wird zunächst aufgrund der Erdanziehung beschleunigt. Dieser Kraft nach unten wirken nach oben der Auftrieb in der Flüssigkeit und die zunehmend größer werdende Reibungskraft entgegen. Gleichen sich diese 3 Kräfte aus, so ist die Gesamtkraft F_ges = 0 und die Kugel sinkt mit konstanter Geschwindigkeit v zu Boden. Diese Reibungskraft hängt u.a. von der Viskosität η ab. Die Formeln  für die auftretenden Kräfte lauten:

Was man also zur Bestimmung von η primär nur tun muss, ist die Geschwindigkeit v der in der Flüssigkeit sinkenden Metallkugel zu bestimmen. Dies kann man entweder manuell mittels Stoppuhr oder automatisiert mittels Lichtschranken und Arduino machen. Als Sinkröhre verwende ich einen Messzylinder mit 50 ml Volumen und die Metallkugel misst 10 mm im Durchmesser.

Für eine konstante Sinkgeschwindigkeit heben sich wie schon erwähnt die drei Kräfte Gewicht, Auftrieb und Reibung auf. Man kann dann die erhaltene Gleichung sehr einfach nach der Viskosität η auflösen und erhält:

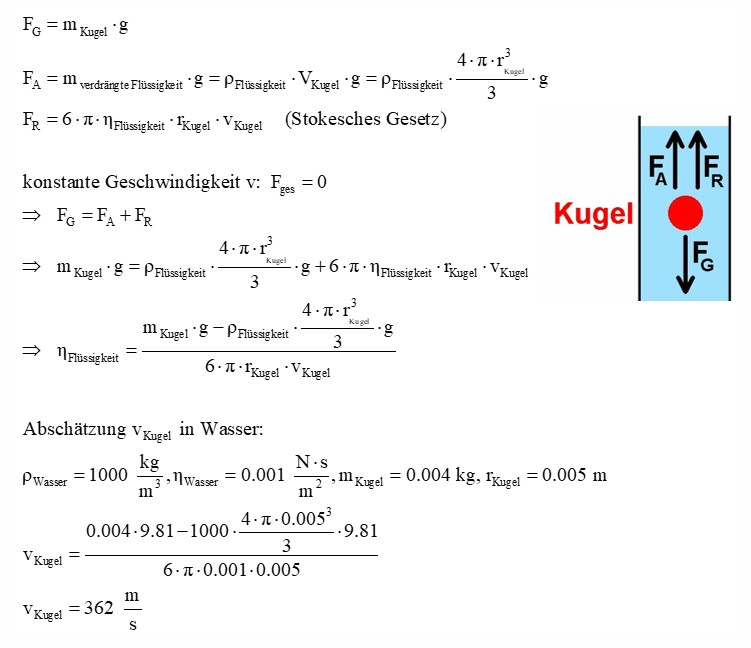
An dem konkreten Beispiel mit Wasser als Flüssigkeit erkennt man aber, dass hier etwas nicht stimmen kann. Die mit der Formel berechnete Sinkgeschwindigkeit müsste für eine Metallkugel mit r = 5 mm und m = 4 g stolze 362 m/s betragen, was natürlich nicht stimmen kann. Was ist hier aber falsch?

Die allgemeine Formel für Reibungskräfte in Flüssigkeiten und Gasen lautet:

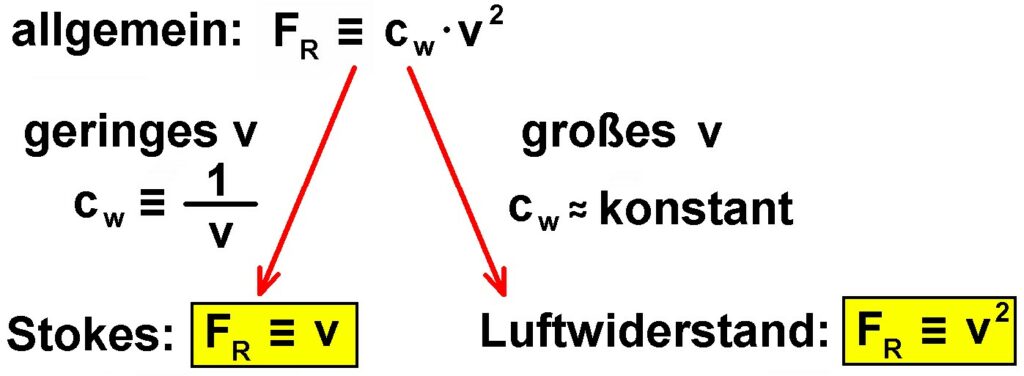
Nur für geringe Geschwindigkeiten/laminare Verhältnisse erhält man also die lineare Beziehung nach Stokes, wohingegen man für höhere Geschwindigkeiten/turbulente Verhältnisse eine quadratische Abhängigkeit erhält.

Anstelle der Geschwindigkeit gibt man oft die sog. Reynoldszahl Re an. Diese besitzt keine Dimension, ist also eine reine Zahl ohne Einheit und in ihr steckt unter anderem auch die Geschwindigkeit v. Vereinfacht ausgedrückt besitzen Strömungen mit der gleichen Reynoldszahl dieselben Strömungsverhältnisse. Dies ist etwa bei der Miniaturisierung von Strömungssimulationen wichtig.

Trägt man den Widerstandsbeiwert (= cw-Wert) in Abhängigkeit von v bzw. der Reynoldszahl auf, so erhält man folgenden Graphen:

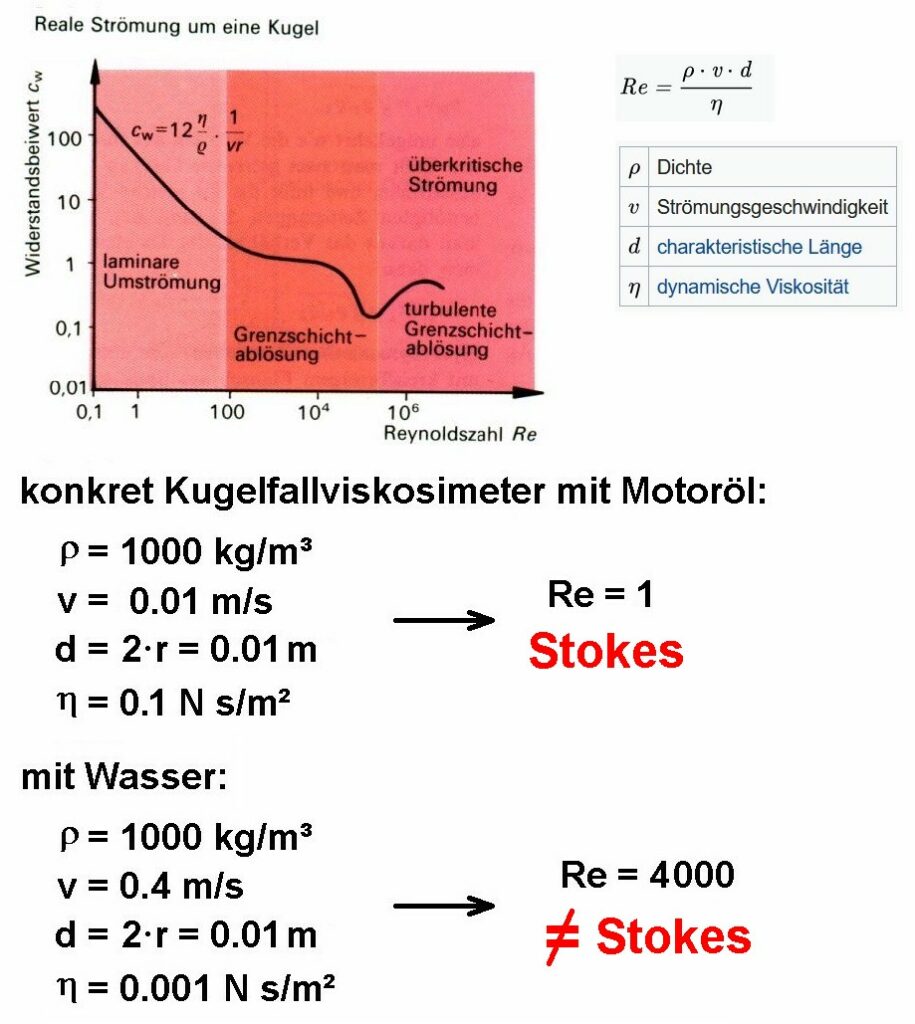
Wie man sieht, liegt im Fall von Motoröl die Stokes-Reibung vor, bei Wasser jedoch nicht mehr! Daher stimmt die obige Formel zur Berechnung der Viskosität η für Wasser nicht. Für zähere Flüssigkeiten wie Öle oder Honig ist sie jedoch legitim.

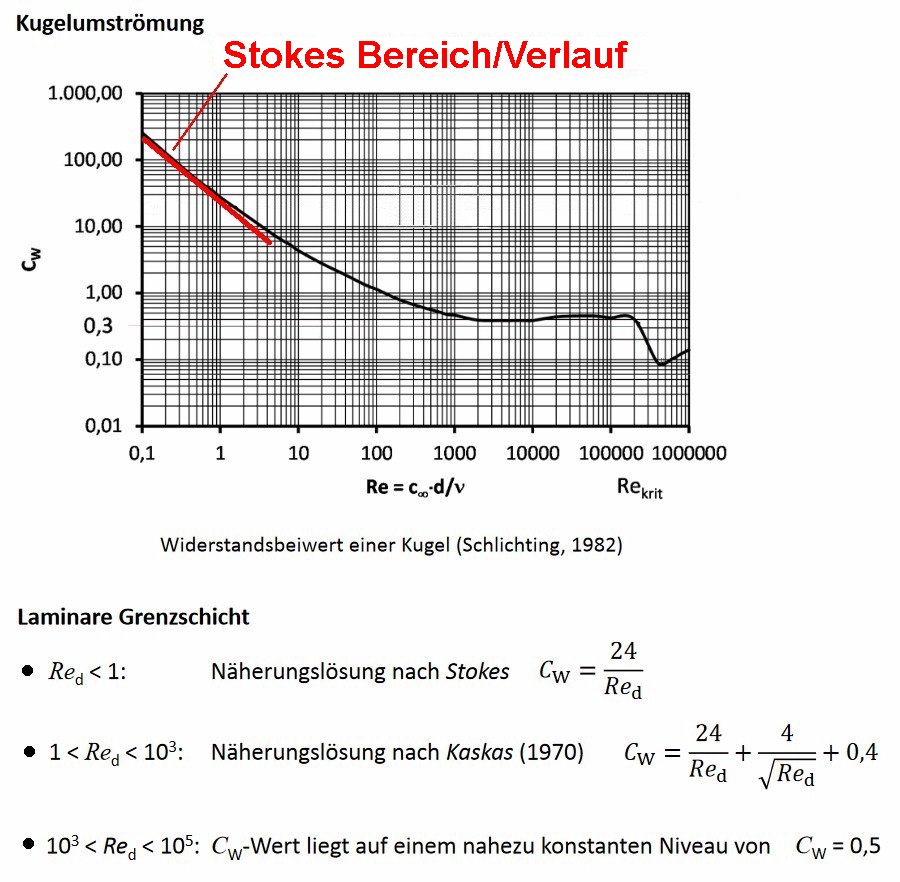
Quelle: http://hakenesch.userweb.mwn.de/fluidmechanik/k5_folien.pdf

Hier nun der Schaltplan mit Arduino. Die beiden IR-LEDs werden in Serie und mit einem Vorwiderstand (ca. 50 Ω) an den 5V-Pin des Arduino geschlossen. Ebenso wie eine Taster/Widerstandkombination, mit dessen Hilfe dann die Programmausführung gesteuert werden kann. Das Potentiomter dient dazu, die Masse m für verschieden schwere Flüssigkeiten für das fixe Volumen von 50 ml (= Volumen des verwendeten Messzylinders) eingeben zu können. Eingelesen wird hier über den analogen Eingang A0. Die beiden Lichtschranken verfügen über eine Serienschaltung einer Photodiode mit einem 47 kΩ Widerstand. Die an diesem abfallende elektrische Spannung wird jeweils mit einem analogen Eingang (A1 und A2) des Arduino gemessen

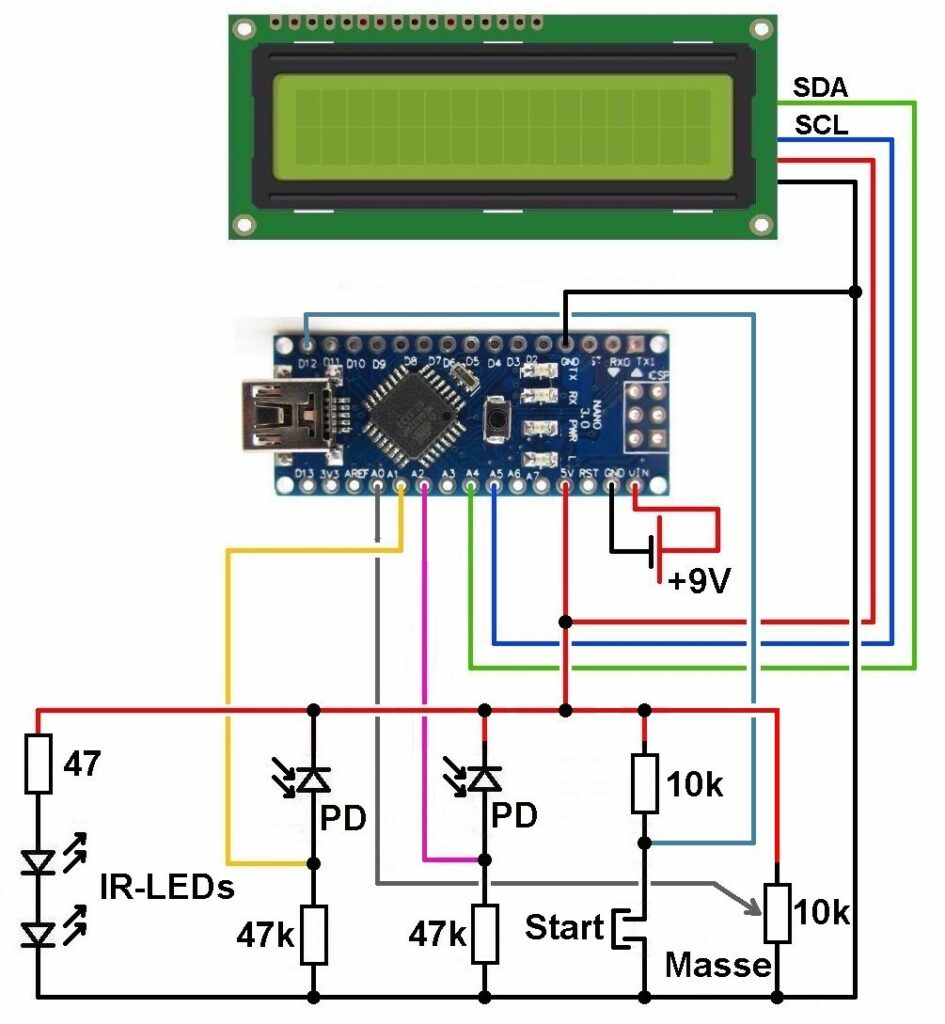
Ob ich die LEDs und Photodioden jeweils gegenüber voneinander anordne oder ich auf eine Reflexionslichtschranke zurüchgreife, müssen erste Praxistests mit der sinkenden Kugel zeigen. Hier das simple Messprinzip mit den beiden Lichtschranken:

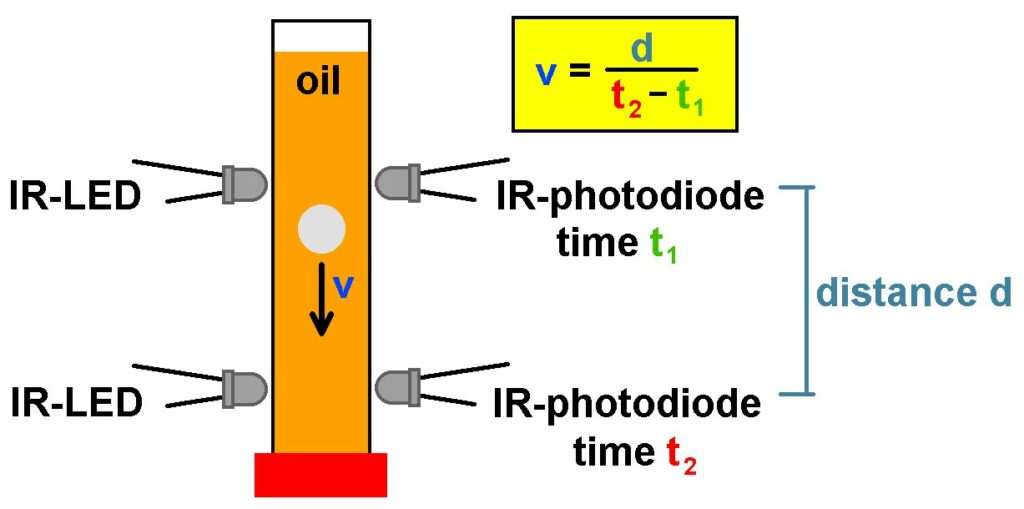
Zwei 50 ml-Messzylinder sind heute mit der Post angekommen. Jetzt müssen nur noch IR-LEDs und die Photodioden verbaut werden, dann kann eigentlich die erste Messung mit dem Viskosimeter erfolgen.

Der erste Test der Lichtschranken ist absolviert. Ehrlich gesagt hätte ich einen deutlicheren Einbruch der Spannung erwartet. Ich habe es aber erstmals nur mit Wasser ausprobiert und da sinkt die Kugel sehr schnell. Bei Verwendung eines Öls mit dementsprechend geringerer Sinkgeschwindigkeit kann es dann auch noch einmal anders aussehen.

Ich habe beide Varianten ausprobiert: LED und Photodiode auf derselben Seite und dann einander gegenüber. Die etwas besseren Ergebnisse erziele ich mit der zweiten Anordnung. Diese werde ich dann wohl auch final umsetzen.

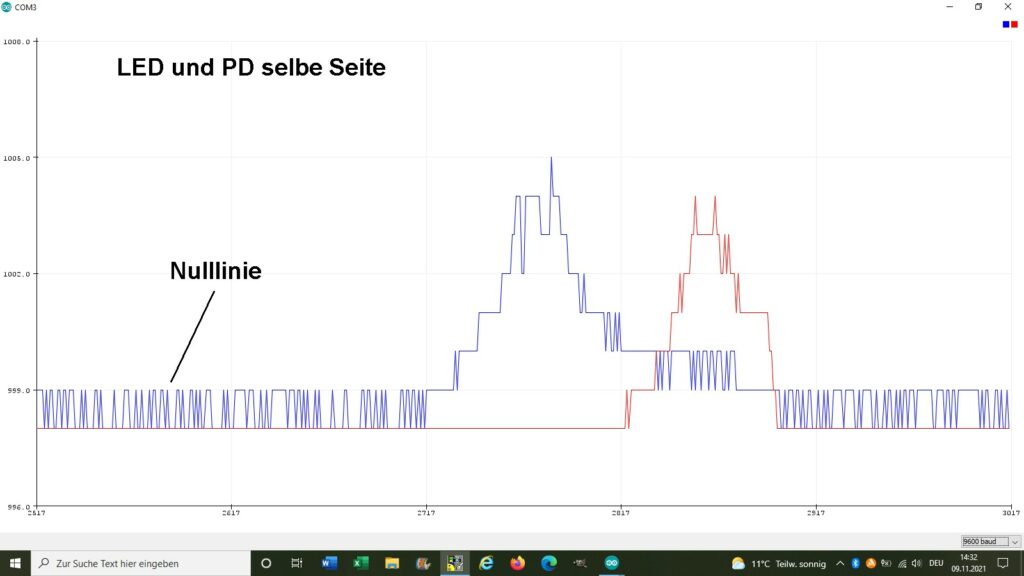
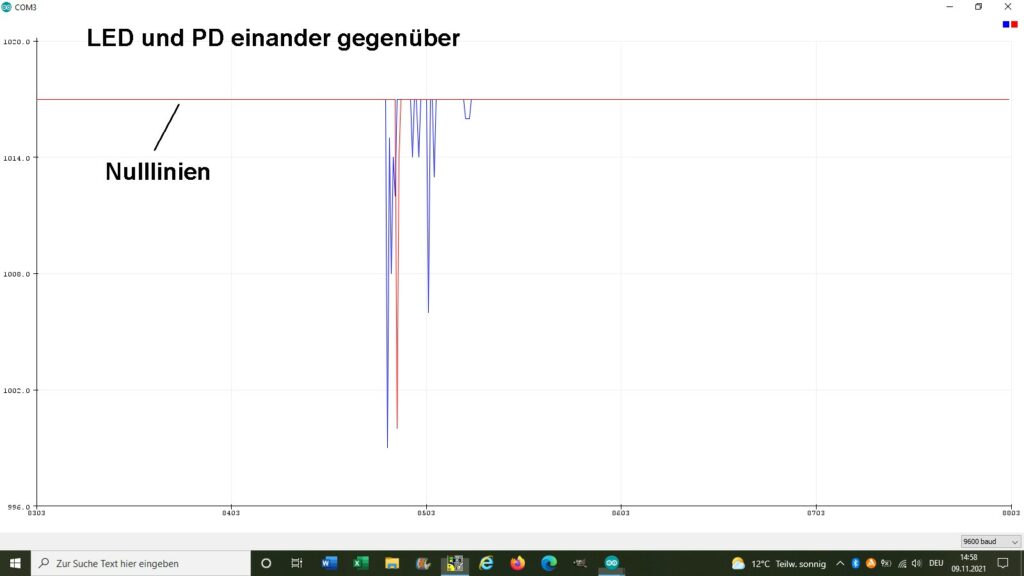
Der Anstieg um gerade einmal 6 bei der ersten Variante (8 bit Auflösung, also mögliche Eingangswerte von 0 bis 1023) bzw. der Abfall um 18 bei der zweiten Variante sind wie gesagt nicht gerade berauschend. Ich werde aber dennoch hoffentlich zuverlässig mit ihnen arbeiten können.

Das schlechte Ansprechen der Lichtschranken hat mir keine Ruhe gelassen. Habe daher die Lichtschranken mit 940 nm IR-LEDs und 700-1200 nm IR-Photodioden (maximale Empfindlichkeit auch bei 940 nm) neu aufgebaut. Und siehe da, jetzt sprechen die Lichtschranken deutlich besser auf die sinkende Kugel an. Bei Abdunkelung fallen die Werte von ca. 340 auf nahezu 0 ab. Damit bin ich mehr als zufrieden.

Jetzt folgt nur noch die Suche nach einer Kugel mit niedriger Dichte um die 2 g/cm³.  Mir fallen ad hoc Glasmurmeln, Edelsteinkugeln oder Gummibälle ein. Mal schauen, was ich so in den Geschäften finde…

Auf der Suche nach einer passenden Murmel mit einer Dichte zwischen 1.2 und 2.7 g/cm³ bin ich “teilweise” fündig geworden in Form einer Plastikperle. Damit ich diese aber schwerer mache, habe ich in die Perlenöffnung Lötzinn gestopft. Jetzt beträgt die Dichte rund 1.7 g/cm³, was wohl sehr gut passen sollte. Honig hat ja immerhin eine Dichte von beachtlichen 1.40-1.45 g/cm³.

Ich konnte heute den Versuch mit Sonnenblumenöl durchführen. Es ergab sich bei einer Temperatur des Öls von rund 10°C eine Viskosität η = 0.454 Pa·s. Dieser Wert ist ein wenig zu hoch, wenn ich mir die Tabellenwerte im Internet so anschaue. Ich erhielt aber bei mehrmaligen Durchläufen immer eine Viskosität in diesem Bereich. Gut, Präzisionsgerät ist es wohl nicht 😉

Das Youtube-Video reiche ich noch nach…

---

Arduino-Code: