Hier (https://stoppi-homemade-physics.de/lichtgeschwindigkeit-arduino/) habe ich eine einfache Methode präsentiert, mit dem ToF Sensor VL53L0X und Arduino die Lichtgeschwindigkeit zu bestimmen.
Es gibt aber auch andere zum Teil sehr elegante Methoden zur Bestimmung von c. Im Vakuum beträgt die Lichtgeschwindigkeit ja c = 299 792 458 m/s. Sie ist laut spezieller Relativitätstheorie die absolute Obergrenze für Geschwindigkeiten. Grund dafür ist, dass die Masse mit zunehmender Geschwindigkeit zunimmt und für v ⇒ c unendlich groß wird. Daher würde für sämtliche massebehaftete Körper eine unendlich große Energie notwendig sein. Photonen mit der Ruhemasse 0 können aber ohne Probleme sich mit Lichtgeschwindigkeit bewegen. Auch Teilchen in Teilchenbeschleunigern besitzen Geschwindigkeiten, die nur mehr marginal von c abweichen.
Die Einschränkung, dass sich im Vakuum nichts schneller als Licht bewegen kann, gilt für ein Medium mit einem Brechungsindex n > 1 nicht mehr. Wasser besitzt zum Beispiel für sichtbares Licht einen Brechungsindex von n ≈ 4/3. Demnach beträgt die Lichtgeschwindigkeit in Wasser “nur” mehr cWasser = cVakuum / nWasser = 3·10^ 8 / (4/3) = 225 000 km/s. Massebehaftete Teilchen wie etwa kosmische Myonen können aber durchaus mit einer Geschwindigkeit v > cWasser in einen Wassertank eindringen. Bei der dann stattfindenden Abbremsung senden sie Licht, sog. Cherenkov-Strahlung ab. Wird dieses schwache Licht etwa mit einem Photomultiplier detektiert, können Myonen gezählt werden (siehe https://stoppi-homemade-physics.de/cherenkovdetektor-fuer-myonen/).
Variante 1: Lichtpulse
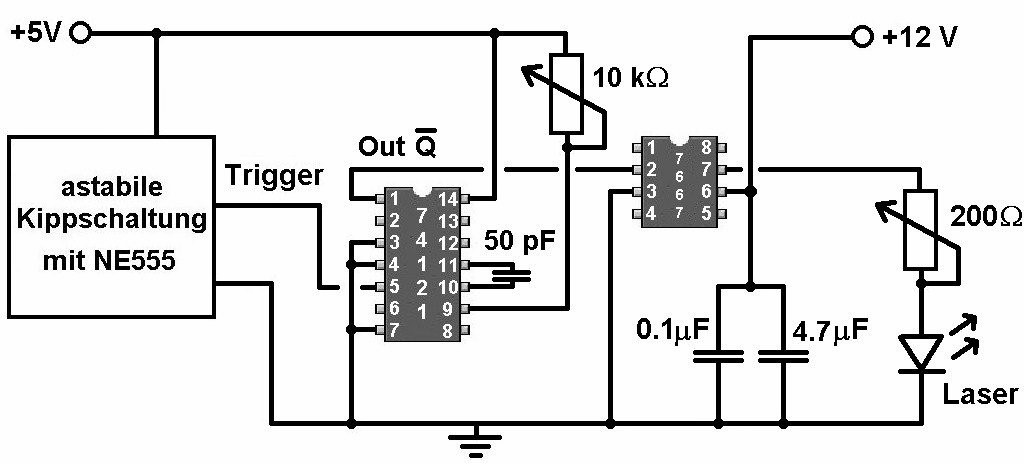
Bei dieser Variante zur Bestimmung der Lichtgeschwindigkeit werden mit einem Laser sehr kurze (ca. 100 ns lang) Lichtpulse ausgesendet. Getriggert werden diese Pulse mittels einer astabilen Kippstufe, welche eine Frequenz von zum Beispiel 10 Hz besitzt. Dieser Triggerpuls wird aber nun nicht nur an die Laseransteuerung gesandt, sondern auch an den externen Triggereingang eines Oszilloskops. Das Oszilloskop bekommt also 10 mal pro Sekunde den Befehl, mit der Aufzeichnung zu starten.

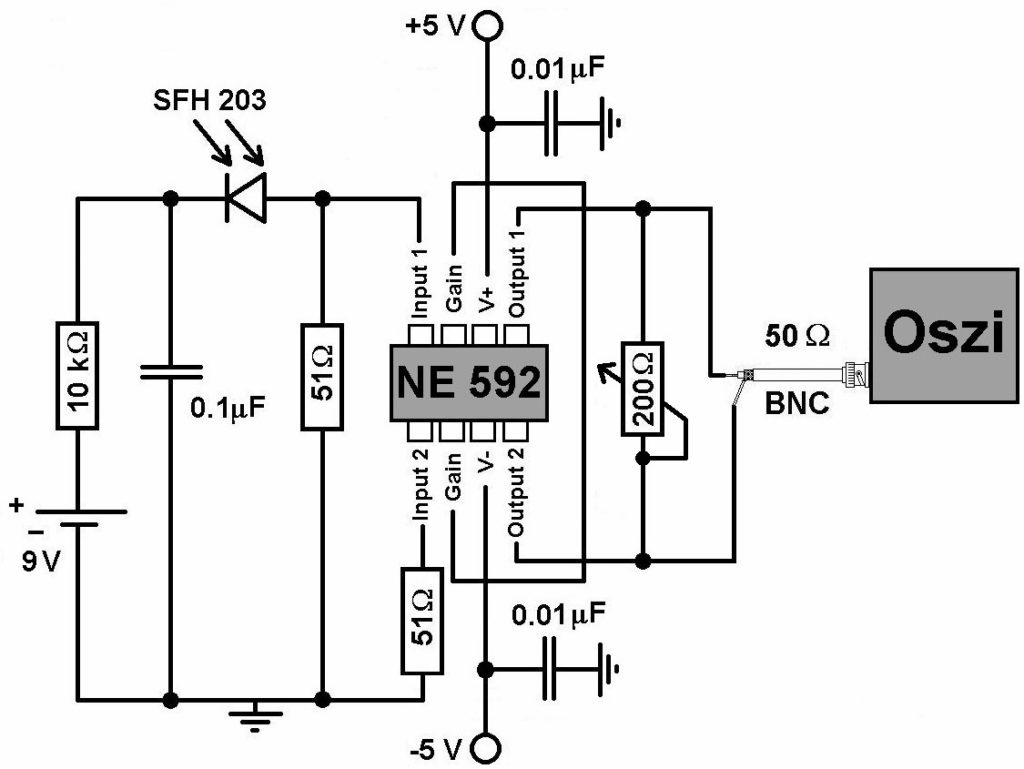
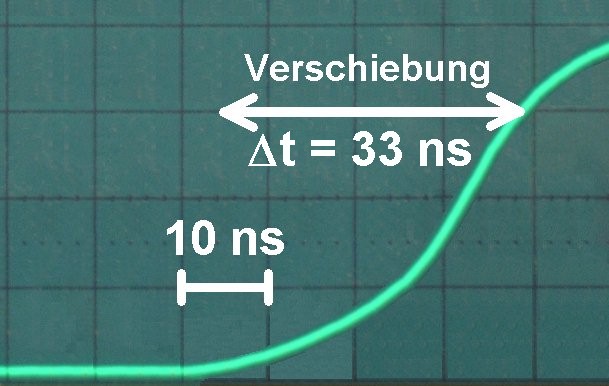
Die kurzen Laserpulse treffen auf einen sehr schnellen Lichtdetektor. Dessen Ausgangssignal wird nun ebenfalls mit dem Oszilloskop erfasst. Trifft der Laserpuls auf den Lichtdetektor, so erzeugt er am Ausgang einen sehr kurzen Spannungspuls. Nun ist der Lichtdetektor über ein 10 m langes BNC-Kabel mit dem Oszilloskop verbunden. Das Startsignal zur Aufzeichnung erhält das Oszilloskop immer zur selben Zeit. Der Zeitpunkt, wann der Laserpuls auf den Lichtdetektor trifft, hängt jedoch von der Entfernung des Lichtdetektors zum Laser ab. Wird diese Entfernung zum Beispiel erhöht, so treffen die Laserpulse etwas später auf den Lichtdetektor und der Spannungspuls an dessen Ausgang wird ebenfalls etwas später an das Oszilloskop weitergeleitet. Daher erscheint der Spannungspuls auf dessen Bildschirm nun nach rechts verschoben.
Aus der Ortsverschiebung Δs des Lichtdetektors und der daraus resultierenden Zeitverschiebung Δt am Oszilloskop lässt sich ganz einfach die Lichtgeschwindigkeit c berechnen und zwar gilt: c = Δs / Δt.
Schaltplan des Laserpuls-Generators:
Schaltplan des schnellen Lichtdetektors:



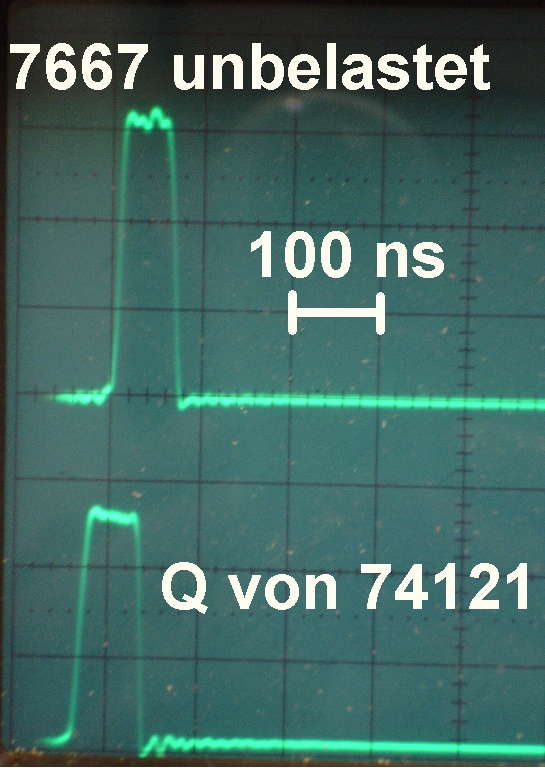
Nach Verschiebung des Lichtdetektors um 10 m ergibt sich folgendes Bild am Oszilloskop:

Variante 2: Mikrowelle
Man kann es kaum glauben, aber die Lichtgeschwindigkeit lässt sich sogar in der Küche mit einer Tafel Schokolade und einer Mikrowelle bestimmen.

Man legt einfach die große Tafel Schokolade in die Mikrowelle, wobei der Drehteller deaktiviert werden muss. Nach einiger Zeit entnimmt man dann die Schokolade und bestimmt den Abstand d der geschmolzenen Stellen. Wie kann man nun aber aus d die Lichtgeschwindigkeit c bestimmen?
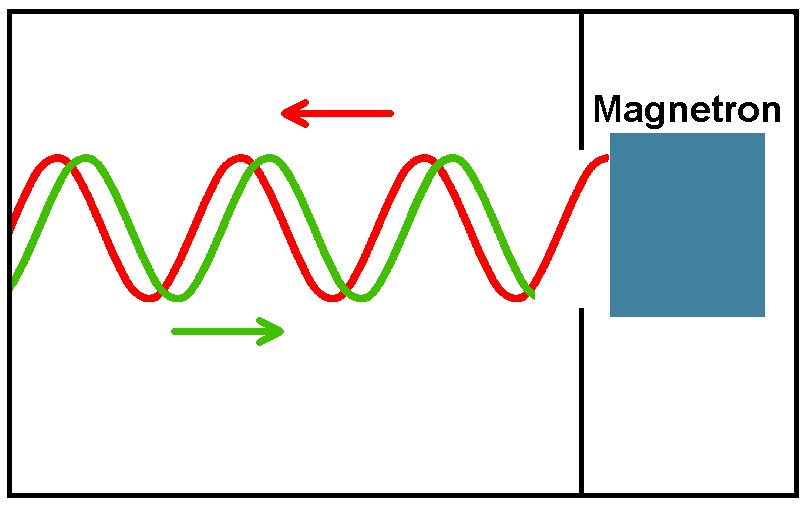
Nun, im Innenraum der Mikrowelle werden die Mikrowellen (deren Frequenz beträgt 2.4 GHz) an der Wand reflektiert. Ausgestrahlte (blaue Welle) und reflektierte Welle (orange Welle) überlagern sich und erzeugen eine sog. stehende Welle (grüne Welle).
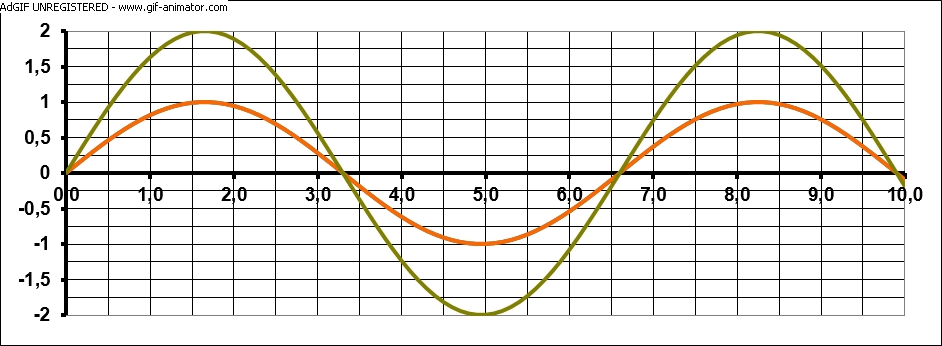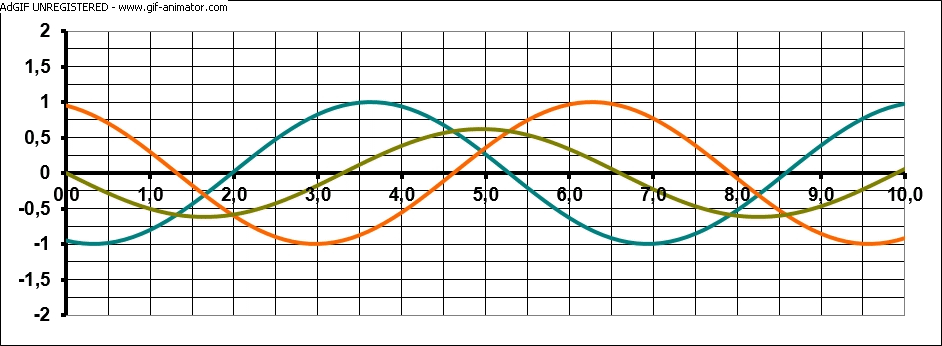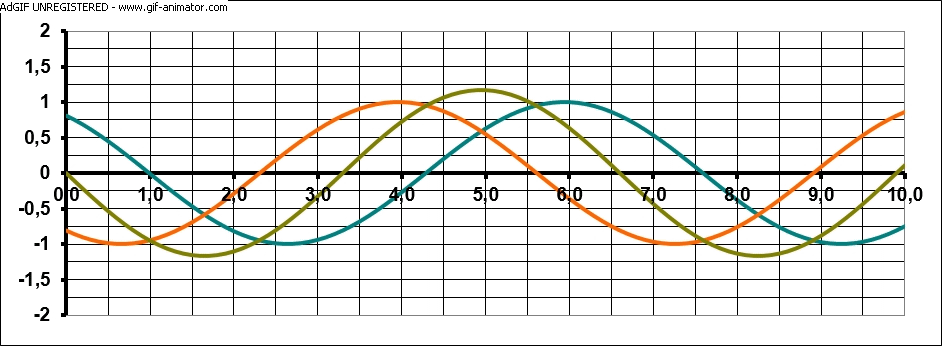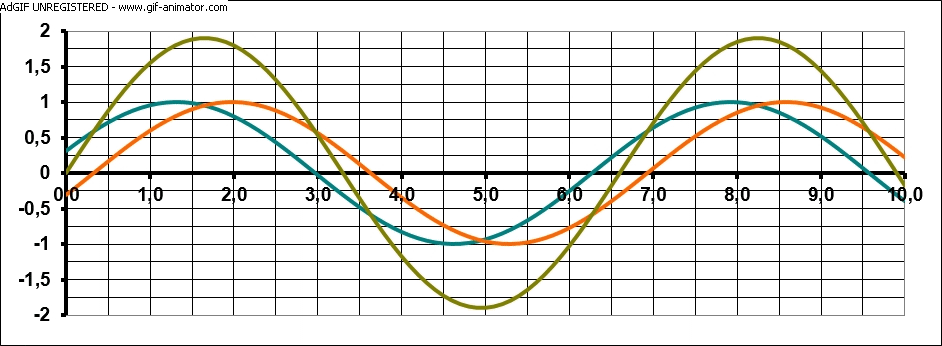
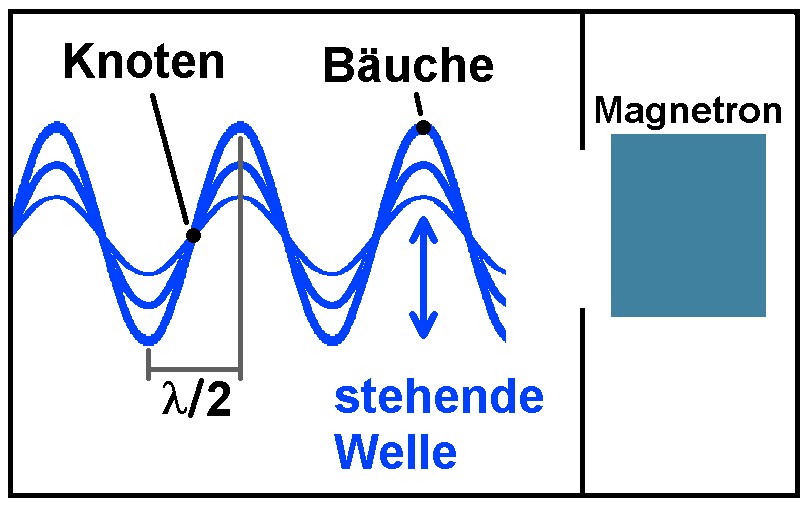
Wie man sieht, bleibt die stehende Welle ortsfest, sprich ihre Maxima und Minima wandern nicht mehr. Der Abstand zweier Schwingungsbäuche beträgt genau die halbe Wellenlänge λ/2. An diesen Stellen schmilzt aber auch die Schokolade, sprich d = λ/2. Es gilt aber auch die sog. Wellengleichung: c = λ · f. Die Frequenz f der Mikrowellen kennen wir mit 2.45 GHz und die Wellenlänge λ = 2 · d können wir durch den Abstand d der geschmolzenen Schokoladenstellen berechnen.



Hier die kurze Herleitung der Wellengleichung und die Berechnung der Lichtgeschwindigkeit:
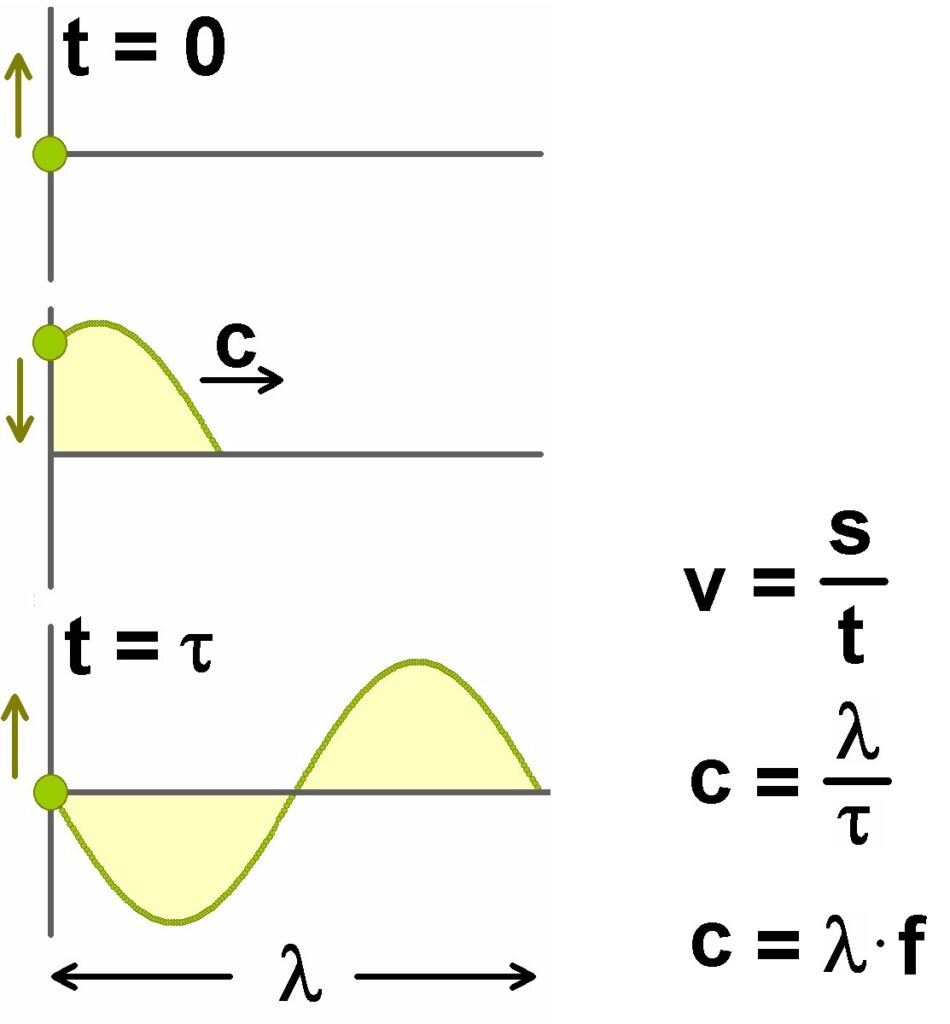


Konkret gilt d = 6 cm = 0.06 m. Daraus folgt für die Wellenlänge λ = 2 · d = 0.12 m. Eingesetzt in die Wellengleichung folgt für die Lichtgeschwindigkeit: c = λ · f = 0.12 · 2.45 · 10^ 9 = 2.94 · 10^ 8 m/s.
Variante 3: Lichtleiterkabel
Diese Variante verwendet die Pulsschaltung der Variante 1. Die kurzen Laserpulse werden aber in ein Lichtleiterkabel eingekoppelt, an dessen Ende sich eine Photodiode befindet. Auf eine weitere Photodiode treffen die Laserpulse direkt ohne Umweg durch das Glasfaserkabel. Aus der Zeitdifferenz der beiden ankommenden Pulse kann die Lichtgeschwindigkeit im Lichtleiterkabel ermittelt werden.
Das 50 m lange Lichtleiterkabel gibt es bei Aliexpress für kleines Geld:
Den halbdurchlässigen Spiegel bekommt man bei AstroMedia bzw. PGI:
Der gesamte Schaltplan bzw. Aufbau:



Die beiden schnellen Photodioden vom Typ SFH203:



Hier das mit einer der beiden Photodioden empfangene Signal:

Damit der detektierte Puls durch die Eingangskapazität des Oszilloskops zeitlich nicht stark gedehnt wird, muss der Tastkopf auf 1:10 umgestellt und zudem der Widerstand in Serie mit der Photodiode (konkret ein 5 kΩ-Potentiometer) recht klein gewählt werden. Tut man dies nicht, sieht das empfangene Signal nämlich so aus:
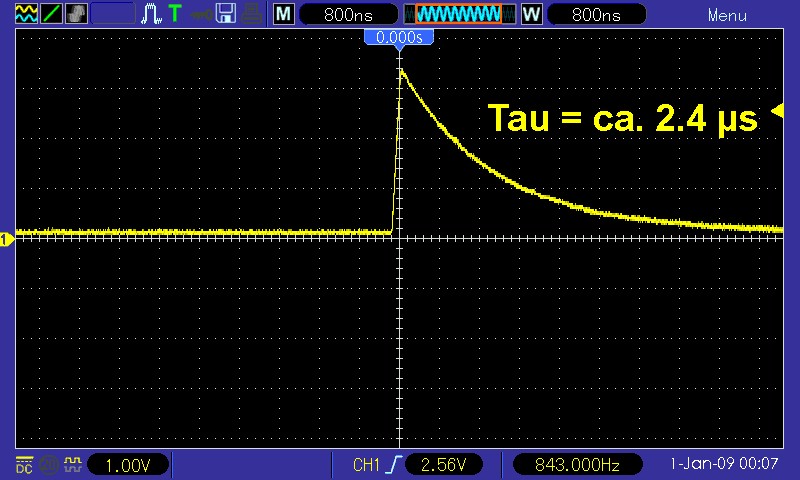
Deutlich ist die für einen Kondensator typische Entladekurve zu erkennen. Die viel zu große Pulsdauer wäre für diesen Versuch so natürlich unbrauchbar…
Mittlerweile ist das Lichtleiterkabel aus China bei mir angekommen und ich konnte erste Tests machen.

In das Gehäuse der Photodiode habe ich mit einem 0.8 mm Bohrer ein Loch für das Lichtleiterkabel gebohrt.

Damit möglichst wenig Licht gestreut wird und viel am Sensor der Photodiode ankommt, fülle ich das Loch mit Silikonfett, bevor ich das Lichtleiterkabel einführe.

Koppel ich den Laserstrahl mittels der Kollimatorlinse in das Lichtleiterkabel ein, so ist eigentlich auch bei größter Empfindlichkeit des Oszilloskops (10 mV/div) kein Signal detektierbar. Den Aufbau mit zwei Photodioden und dem halbdurchlässigen Spiegel kann ich also vergessen.

Daher kopple ich nun das Laserlicht ein, indem ich den Eingang des Lichtleiterkabels direkt auf das Glas der Laserdiode ganz ohne Kollimator halte. Damit bekomme ich ein Signal in der Höhe von 50-100 mV. Möchte ich den ankommenden Lichtpuls ohne Verzögerung messen, so halte ich die Laserdiode ohne Umweg über den LWL direkt an die Photodiode…
Der gesamte Aufbau:



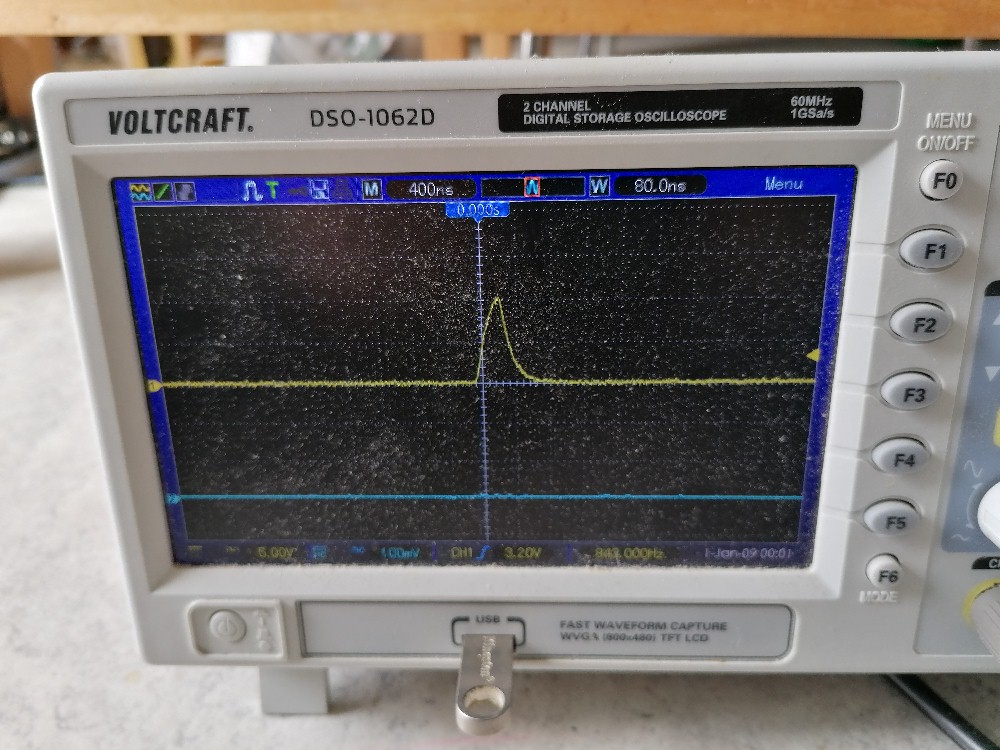
Hier das empfangene Signal ohne Lichtwellenleiter…

… und mit 50 m Lichtwellenleiter dazwischen:
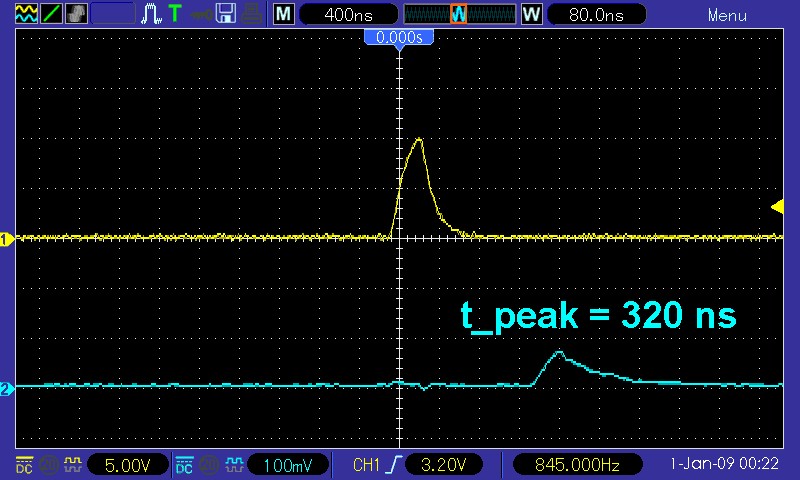
Die zeitliche Verzögerung beträgt also 250 ns bei einer Länge des Lichtleiterkabels von wie gesagt 50 m. Daraus ergibt sich eine Lichtgeschwindigkeit im Medium von c = 200 000 km/s. Der Brechungsindex des LWL beträgt somit 1,5. Laut Recherche im Internet beträgt der Brechungsindex n der Lichtleiterkabel zwischen 1.45 und 1.55, Heureka 🙂

Das Youtube-Video reiche ich natürlich nach…

