Unter der Solarkonstanten versteht man jene Sonnenenergie pro Sekunde und pro m², welche am Ort der Erde (außerhalb der Erdatmosphäre) ankommt. Sie beträgt rund 1370 J/sek·m². also 1.37 kW/m².
Dieser Wert ist aber trotz des Namens keinesfalls eine Konstante, da sich ja schon alleine der Abstand Erde-Sonne ändert. Im Mittel beträgt dieser 150.000.000 km. Auch strahlt die Sonne nicht immer absolut die gleiche Energie ab.
Die auf der Erdoberfläche ankommende Strahlungsintensität ist dann logischerweise durch Absorptions- und Reflexionseffekte innerhalb der Erdatmosphäre geringer und beträgt an einem wolkenfreien Tag rund 500–800 W/m². Je länger der Weg der Sonnenstrahlen durch die Atmosphäre (je tiefer also die Sonne am Himmel steht), desto größer ist diese Abschwächung/Extinktion. Diesen Umstand werden wir uns dann später bei der Berechnung der Solarkonstanten noch zunutze machen (siehe weiter unten).
Die von der Sonne am Ort der Erde empfangene Strahlungsintensität lässt sich aus dem Sonnenspektrum herleiten, dessen Intensitätsverlauf ja der Planckschen Strahlungskurve folgt:

Bildquelle: Wikipedia
Hier das mit meinem Arduino-Spektroskop aufgenommene Sonnenspektrum:
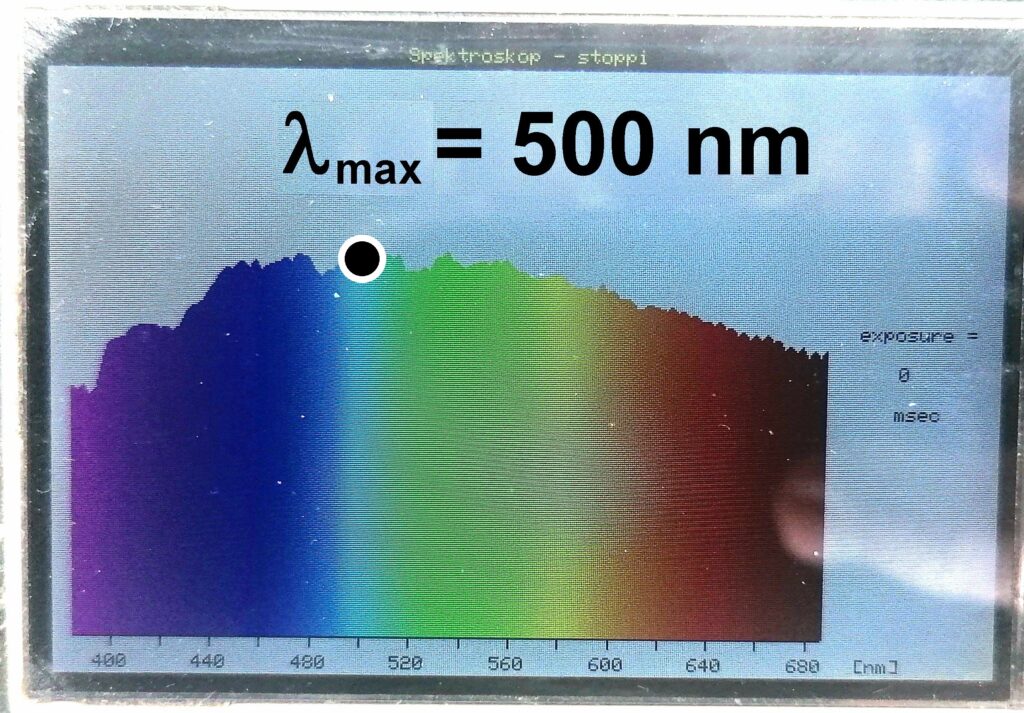
Das Maximum der Planck‘schen Strahlungskurve unserer Sonne liegt bei rund λ = 500 nm. Laut dem Wien‘schen Verschiebungsgesetz beträgt damit die Oberflächentemperatur der Sonne
Nach dem Stefan-Boltzmann-Gesetz emittiert jeder Quadratmeter der Sonnenoberfläche eine Leistung von

Die gesamte Sonnenoberfläche emittiert daher die Leistung

Der Abstand Sonne-Erde beträgt rund 150 Millionen Kilometer (1 astronomische Einheit). Daher kommt pro Quadratmeter am Ort der Erde nur noch folgende Intensität an:
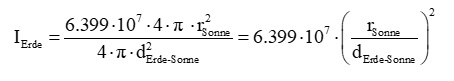
Die Winkelausdehnung der Sonne beträgt von der Erde aus gesehen ca. 0.5°. Daraus lässt sich das Verhältnis rSonne/dErde-Sonne berechnen:

Setzt man diesen Wert in die Formel für die Strahlungsintensität am Ort der Erde ein, erhält man die Solarkonstante:
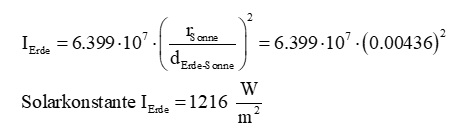
Wie kann man nun diese Solarkonstante experimentell bestimmen? Eine Möglichkeit wäre die Verwendung einer Thermosäule (https://stoppi-homemade-physics.de/thermosaeule/).


Diese besteht aus einem Peltierelement, dessen eine Seite berußt ist. Durch die absorbierte Strahlung erwärmt sich eine Seite des Peltierelements geringfügig und erzeugt auf diese Weise eine geringe Thermospannung. Diese ist direkt proportional zur einfallenden /absorbierten Strahlungsleistung. Die Strahlungsintensität kann dann direkt in W/m² am Display abgelesen werden.

Es gibt aber eine noch viel einfachere Methode zur Bestimmung der Strahlungsintensität/Solarkonstanten. Man nimmt eine 100W-Glühbirne und hält diese in wenigen Zentimetern Entfernung zur Sonnenabgewandten Gesichtswange. Die Sonne strahlt auf die andere Wange. Nun bestimmt man genau jenen Abstand d der Glühbirne zur Wange, bei dem das Wärmegefühl auf beiden Wangen gleich ist. Die menschliche Haut ist diesbezüglich verblüffend sensibel. Ist dies der Fall, sind auch beide Strahlungsintensitäten gleich.
Angenommen der so herausgefundene Abstand beträgt 8 cm. Dann beträgt die Strahlungsintensität der Glühbirne am Ort der Wange genau I_Glühbirne = 100 W / (4·π·0.08²) = 1243 W/m² und den gleichen Wert besitzt auch die Sonnenintensität. Bei dieser Berechnung geht man davon aus, dass sich die Strahlungsleistung der Glühbirne gleichmäßig auf die gesamte Kugeloberfläche 4·π·r² verteilt. Dies ist natürlich nicht wirklich der Fall. Das Ergebnis zeigt aber, dass selbst diese einfache Abschätzung ein mehr als brauchbares Ergebnis liefert.
Eine weitere Möglichkeit zur Bestimmung der Solarkonstanten besteht darin, einen einseitig schwarz gefärbten oder mit Ruß überzogenen Aluminiumblock von der Sonne erhitzen zu lassen. Dies führt zu einer Erhöhung der Temperatur wobei aus dem anfänglichen Verlauf der Temperatursteigerung die Sonnenintensität abgeleitet werden kann.

Die erhaltene Temperaturkurve wird in etwa folgenden Verlauf besitzen:
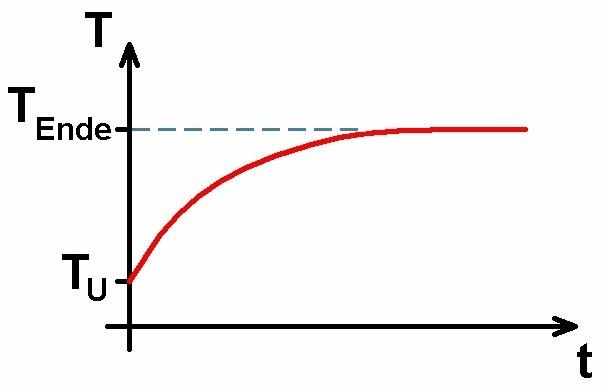
Die Temperatur startet bei der Umgebungstemperatur TU und steigt dann an. Die Temperaturzunahme wird aber immer geringer , sprich die Kurve flacht immer mehr ab. Nach einiger Zeit bei sich sonst nicht veränderten Verhältnissen (d.h. die Aluminiumplatte muss auch der Sonne nachgeführt werden, da sich ja sonst der Einfallswinkel der Strahlen auf die Platte verändern würde) wird sich eine Endtemperatur TEnde einstellen. Für uns wird aber nur der Temperaturverlauf zu Beginn bei t = 0 von Interesse sein. Dazu eine kurze Herleitung:

Wird einem Körper der Masse m mit der spezifischen Wärmekapazität c die Energie/Wärme Q zugeführt, so erwärmt sich dieser um ΔT. Die dazugehörige Formel lautet:
Für die pro Sekunde zugeführte Energie (= Leistung) gilt dann:

Eine Leistung P bedingt also eine sekündliche Temperaturerhöhung dT/dt. Der Absorber bestehe aus einem Material mit der spezifischen Wärmekapazität c, habe eine Masse m und eine wirksame Fläche A. Seine Temperatur sei T, die Temperatur der Umgebung betrage TU. Der Absorber werde von der Sonne mit der Strahlungsleistung PS (= Strahlungsintensität mal Fläche des Absorbers) bestrahlt. Dann ist die Wärmeleistung, die er netto aufnimmt, gegeben durch
Die beiden letzten Ausdrücke entsprechen dem Stefan-Boltzmann-Strahlungsgesetz, welches die abgegebene/aufgenommene Strahlungsleistungs in Abhängigkeit von den Temperaturen beschreibt. Obige Gleichung ist eine Differentialgleichung mit der Lösung T(t). Separation der Variablen führt uns zu
Wie man sieht, ist dieses Integral relativ komplex. Einfacher ist folgender Lösungsansatz: Die beiden Temperaturen T und TU sind annähernd gleich. Nach Taylor kann jede Funktion f(x) wie folgt um den Punkt x0 entwickelt werden:
Setzt man nun diesen Ausdruck für T4 in die Differentialgleichung ein, erhält man:
Probieren wir es für diese nun einfachere Differentialgleichung mit folgenden Lösungsansatz:
Eingesetzt in die Differentialgleichung liefert dies:
Umformen ergibt dann folgende Gleichung:
Die Lösung der Differentialgleichung lautet also schlussendlich:
Für die zeitliche Ableitung der Funktion T(t), also T‘(t) folgt dann daraus:
Daher ergibt sich für die Temperaturänderung unmittelbar zu Beginn (t = 0):
Dies bedeutet, dass unmittelbar nach Beginn der Messung die Temperaturerhöhung ausschließlich durch die Strahlungsleistung PS der Sonne bestimmt ist und die Eigenabbstrahlung der Metallplatte noch keinen Einfluss auf den Temperaturverlauf hat!
Aus dem Anstieg der Kurve T(t) zu Beginn der Messung, also für t = 0, kann also die Strahlungsleistung PS der Sonne ganz einfach ermittelt werden:


Um zur Strahlungsintensität IS zu gelangen, muss PS lediglich durch die Fläche des Absorbers/der Metallplatte dividiert werden. Es gilt dann also:

Wir wissen aber bereits, dass die auf der Erdoberfläche ankommende Strahlungsintensität der Sonne durch die Atmosphäre geschwächt wird. Die gemessenen Intensitäten IS entsprechen also nicht der größeren Solarkonstanten I0, welche ja der Strahlungsintensität außerhalb unserer Atmosphäre entspricht.
Für die Abschwächung entlang des Weges s durch die Atmosphäre folgt dann nach dem Lambert-Beerschen-Gesetz:

Für den Weg s durch die Atmosphäre folgt in Abhängigkeit vom Neigungswinkel α

Dies eingesetzt in die obige Gleichung liefert:
Trägt man also den Logarithmus der gemessenen Strahlungsintensitäten gegen 1/sin(α) auf, so erhält man eine fallende Gerade mit dem Ordinatenabschnitt ln(I0)! Auf diese Weise lässt sich also durch Messung der Strahlungsintensitäten bei unterschiedlichem Sonnenstand (Neigungswinkel α) die Strahlungsintensität I0 im Weltall, die ja der Solarkonstante entspricht, bestimmen!

Experiment
Die Masse des Alublocks beträgt 80 g und dessen Fläche 36 cm². Diese beiden Werte benötige ich ja zur Berechnung der Solarkonstante. Die spezifische Wärmekapazität von Aluminium beträgt c = 896 J/kg·°C.

Das Messgerät ist soweit fertig. Zur besseren Wärmeisolierung ist die Aluplatte in Styropor eingebettet. Die Rundstange dient durch ihren Schattenwurf der senkrechten Ausrichtung der Aluplatte zu den Sonnenstrahlen. Die Vorderfläche der Aluplatte habe ich mit einer Kerzenflamme berust. Damit dürfte der Absorptionsgrad bei ca. 95% liegen.



Heute konnte ich die erste Messung durchführen. Der Neigungswinkel α begtrug 36° und die anfängliche Temperaturerhöhung 0.8 °C innerhalb von 15 Sekunden.





Daher ergibt sich folgender Wert für die Strahlungsintensität:
Bei einem Neigungswinkel α von 23° ermittelte ich eine anfängliche Temperaturerhöhung um 0.7 °C innerhalb von 15 Sekunden.
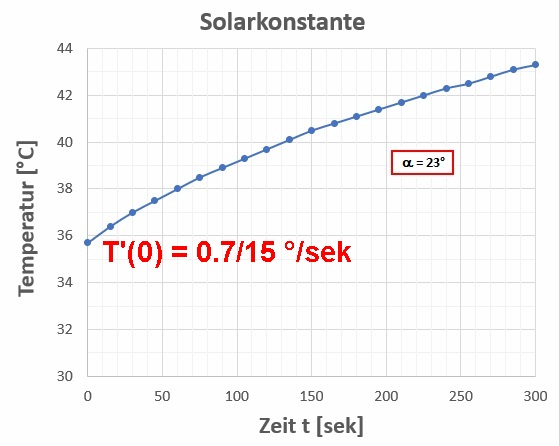
Daraus ergibt sich eine Strahlungsintensität von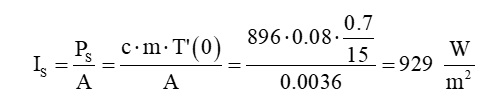
Zur Bestimmung der Strahlungsintensität außerhalb der Erdatmosphäre muss man ln(IS) gegenüber 1/sin(α) auftragen und die Gerade extrapolieren.

Somit erhalte ich für die Solarkonstante schlussendlich folgenden Wert:


