Bildquelle: https://de.wikipedia.org/wiki/Pieter_Zeeman

Der Zeeman-Effekt ist nach dem niederländischen Physiker Pieter Zeeman (25. Mai 1865 – 9. Oktober 1943) benannt. Für seine Verdienste bei den Untersuchungen über den Einfluss des Magnetismus auf die Strahlungsphänomene erhielt er 1902 den Nobelpreis für Physik. Zuerst ein wenig Theorie…

Quantenzahlen

Die Quantenzahlen beschreiben die unterschiedlichen, gequantelten atomaren Zustände. Eng gekoppelt mit den diversen Quantenzahlen ist etwa die Energie der Elektronen bzw. des Kerns, der Drehimpuls bzw. Spin der atomaren Teilchen bzw. die Aufenthaltswahrscheinlichkeit (Orbitale) der Elektronen. Welche Quantenzahlen gibt es nun?

Hauptquantenzahl n = 1, 2, 3 …

Nebenquantenzahl oder Bahnquantenzahl ℓ = 0, 1, 2, … n – 1

Für die unterschiedlichen Nebenquantenzahlen, welche u.a. die Orbitalform beeinflussen, hat man eigene Buchstaben vergeben. Diese lauten: s-Orbital für ℓ = 0, p-Orbital für ℓ = 1, d-Orbital für ℓ = 2, f-Orbital für ℓ = 3 und g-Orbital für  ℓ = 4.

magnetische Quantenzahl m_ℓ = – ℓ, –ℓ + 1, …, ℓ – 1, ℓ

Spinquantenzahl s = ½ (Elektron)

Magnetische Spinquantenzahl m_s = –1/2, +1/2

Damit zusammenhängende Größe = Drehimpulsvektor

Beim Bohrschen Atommodell galt ja folgende gequantelte Bedingung für den Drehimpuls L: Zwischen dem Betrag des Drehimpulses und der Nebenquantenzahl ℓ besteht folgender Zusammenhang:Für die z-Komponente des Drehimpulses gilt zudem

Beispiel: Drehimpulsvektor L und z-Komponente L_z für ℓ = 2

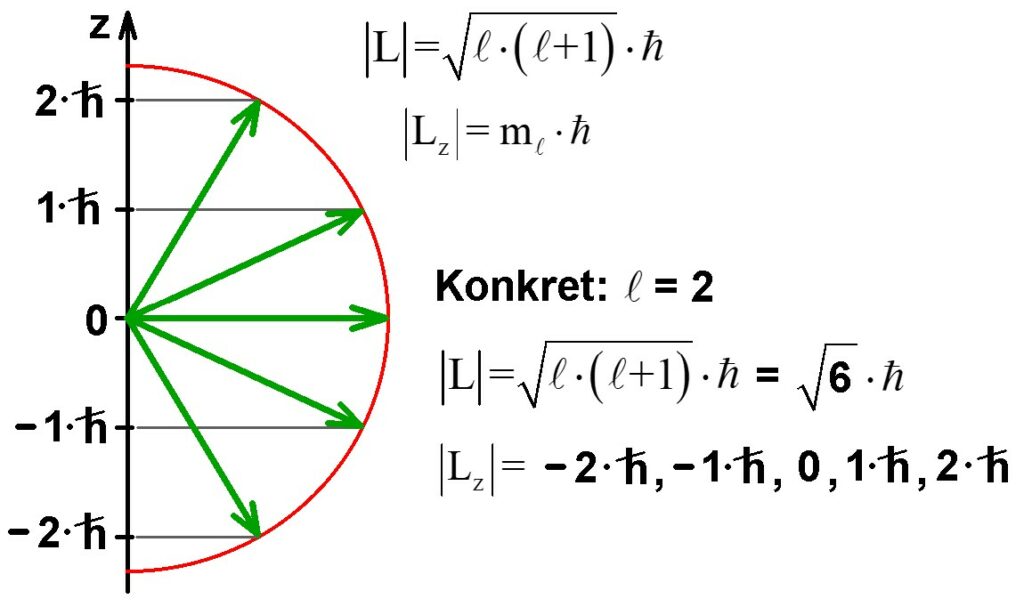
Jetzt könnte man sich fragen, woher ein Atom/Elektron die räumliche Orientierung (z-Achse) überhaupt kennt? Diese Vorzugsrichtung wird erst durch das Vorhandensein eines elektrischen oder magnetischen Felds und dessen räumliche Ausrichtung initialisiert! Fehlt ein solches, ist die jeweilige z-Achse quasi beliebig.

Zusammenhang Drehimpuls – magnetisches Moment:

Kreist das negativ geladene Elektron auf seiner “Bahn” um den Atomkern, so kann es als Kreisstrom betrachtet werden.

Dieser Kreisstrom erzeugt wie ein Elektromagnet ein Magnetfeld. Das Elektron erzeugt/besitzt also ein sog. magnetisches Moment μ.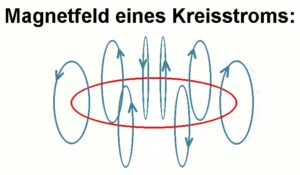

Man kann sich diesen durch die Bewegung des geladenen Elektrons verursachten magnetischen Dipol (mit dem magnetischen Moment μ) wie einen kleinen Stabmagneten vorstellen.

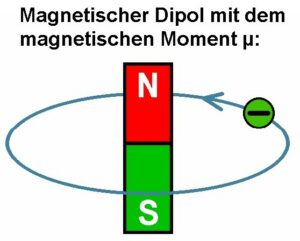
Dieses magnetische Moment μ lässt sich wiefolgt berechnen: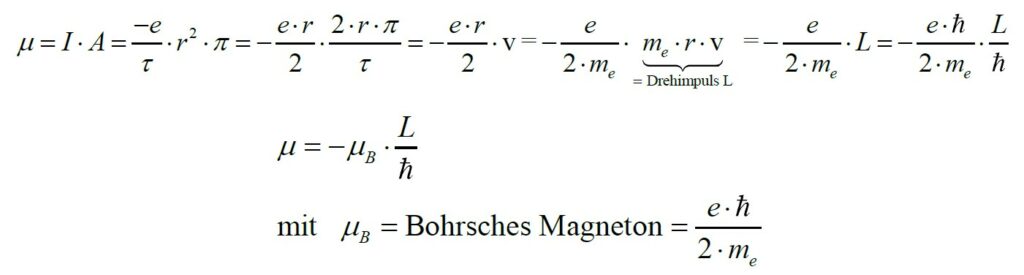

L kann nun der Bahndrehimpuls bzw. der Eigendrehimpuls (= Spin) des Elektrons sein. Im letzteren Fall führt dies zu der sog. Feinstrukturaufspaltung der Spektrallinien!

Bei der Magnetresonanz befindet sich der zu untersuchende Patient in einem (starken) äußeren Magnetfeld B. Dieses wechselwirkt nun mit dem magnetischen Moment des Elektrons. Wie sieht aber diese Wechselwirkung genau aus? Stellen wir uns hierfür weiter den magnetischen Dipol als einen kleinen Stabmagneten vor.

Auf den Stabmagneten bzw. den magnetischen Dipol wirkt im äußeren Magnetfeld ein Kräftepaar und daher ein Drehmoment T. Dieses möchte den Stabmagneten parallel zum Magnetfeld ausrichten, also für einen Winkel α = 0° sorgen. Das wirkende Drehmoment wäre dann bei α = 0° verschwunden, bei α = 90° maximal und bei α = 180° wieder 0. Dieser Verlauf entspricht jenem einer Sinusfunktion.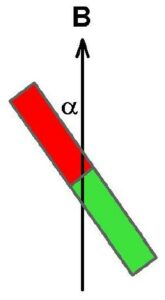

Die exakte Formel für das Drehmoment T lautet:

Nun ist das magnetische Moment μ aber mit einem Drehimpuls L gekoppelt (siehe obige Formel mit dem Bohrschen Magneton). Wirkt nun ein Drehmoment T auf einen Drehimpuls L, so kommt es gemäß der Beziehung T = dL/dt zu einer Ausgleichsbewegung, der sog. Präzession. Dies ist zum Beispiel auch bei einem sich drehenden Kreisel der Fall, welcher gegenüber der Senkrechten eine gewisse Neigung aufweist. Hier kommt das Drehmoment T aber nicht durch ein Magnetfeld sondern durch die Schwerkraft zustande.

Ebenso wie der Kreisel um die Senkrechte „torkelt“, torkelt nun der Drehimpuls des Elektrons mit der sog. Lamorkreisfrequenz ω_Lamor und verhindert dadurch eine Parallelausrichtung zum Magnetfeld. Diese Lamorfrequenz lässt sich auch berechnen. Es gilt:

Die Lamorfrequenz ist unabhängig vom Drehimpuls L und α, sie hängt aber von der Stärke des Magnetfelds B ab. Je stärker das Magnetfeld, desto schneller präzessiert der „Elektronenkreisel“.

Dies kann man auch schön mit diesem Beispiel verdeutlichen: Eine Kompassnadel wird in die Nähe eines Stabmagneten gebracht und in Schwingung versetzt. Nahe beim Stabmagneten, also im stärkeren Magnetfeld, schwingt die Kompassnadel schnell. Weiter weg, wo das Magnetfeld schwächer ist, schwingt sie hingegen langsamer. Mit der Lamorfrequenz verhält es sich ähnlich.

Das äußere Magnetfeld B möchte also den magnetischen Dipol parallel zu sich ausrichten. Wie hängt dies nun mit der potenziellen Energie des magnetischen Dipols im äußeren Magnetfeld zusammen? Da das System in den energieärmsten Zustand strebt, scheint also eine parallele Ausrichtung des magnetischen Dipols bzw. des magnetischen Moments μ zu den Feldlinien B die geringste Energie zu besitzen.

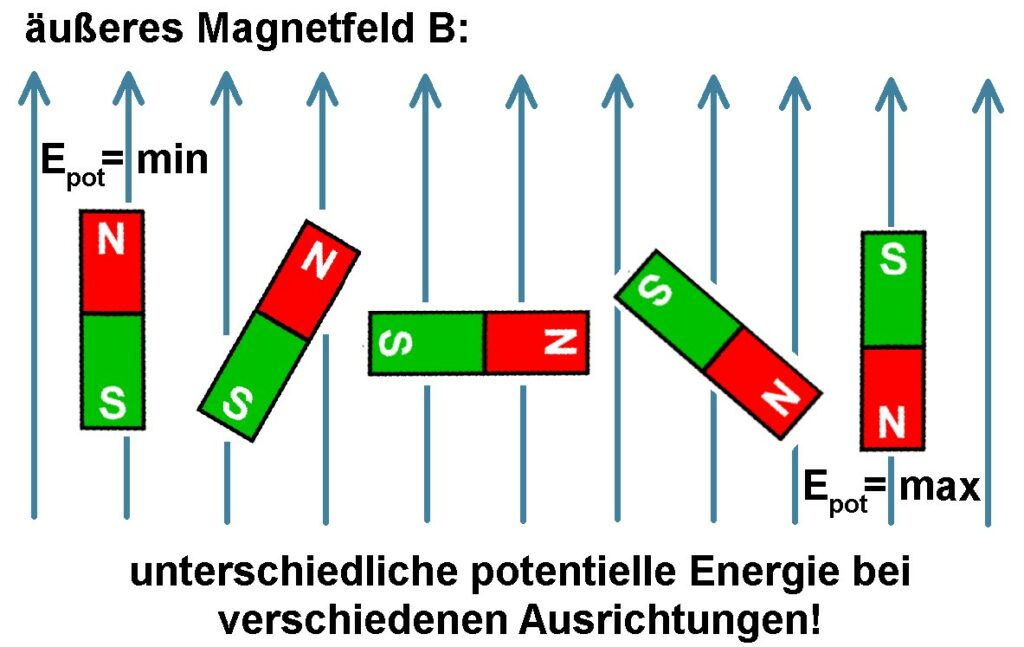
Was die potenzielle Energie betrifft so ist diese minimal, wenn der magnetische Dipol bzw. sein magnetisches Moment in B-Richtung ausgerichtet ist (Winkel α = 0°) und maximal in entgegengesetzter Richtung (Winkel α = 180°). Die potenzielle Energie verläuft also wie die negative Cosinusfunktion. Dies führt uns zur Formel für E_pot.

Für diese gilt:Die potenzielle Energie durch die unterschiedliche Lage des magnetischen Moments μ des Elektrons im äußeren Magnetfeld hängt also von der z-Komponente L_z des Drehimpulses ab, also jener Komponente in Richtung des Magnetfelds!

Diese z-Komponente des Drehimpulses kann bei gegebener Nebenquantenzahl ℓ aber nur die Werte m_ℓ = –ℓ, –ℓ + 1, …,0, …, ℓ – 1, ℓ annehmen. Die möglichen potenziellen Energien sind also auch gequantelt und gehorchen folgender Formel:

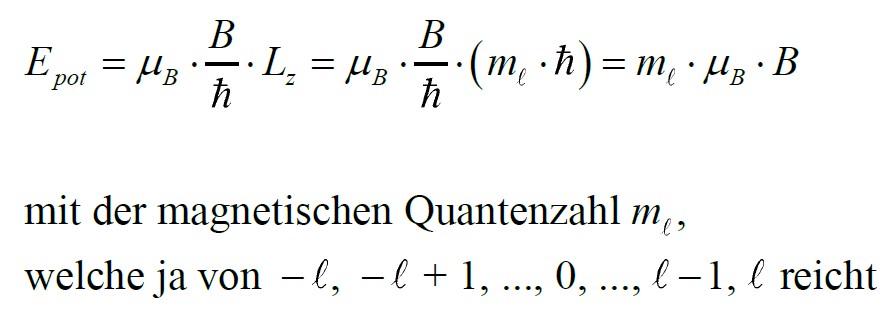
Man nennt daher die Quantenzahl m_ℓ auch magnetische Quantenzahl, da deren Wert für die Energie des Elektrons in einem Magnetfeld relevant ist!

Genau diese unterschiedliche potenzielle Energie führt in einem (äußeren) Magnetfeld also zu einer energetischen Aufspaltung der Niveaus. Wie man anhand der Formel für E_pot erkennen kann, nimmt die Energieaufspaltung linear mit der Stärke B des Magnetfelds zu. Die Termschema bei unterschiedlichen Magnetfeldern sehen daher wie folgt aus:

Licht (Photonen) wird ja beim Übergang des Elektrons von einem Energieniveau in ein tiefer gelegenes emittiert. Wenn nun durch das äußere Magnetfeld diese Niveaus aufspalten, so kann nun das Elektron andere Sprünge als ohne Magnetfeld ausführen. Demnach werden nun verglichen mit dem Fall „kein Magnetfeld“ Photonen mit abweichenden Frequenzen emittiert. Man spricht dann von der sog. Zeeman-Aufspaltung oder dem Zeeman-Effekt!

Diese Energieaufspaltung E_pot ist wie schon erwähnt gemäß der Formel

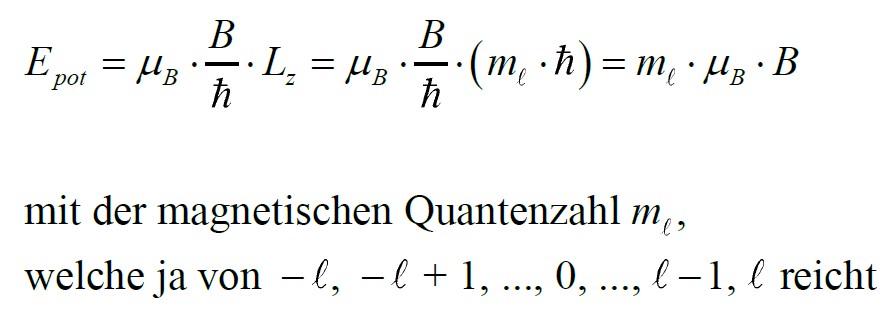
direkt proportional zum herrschenden Magnetfeld B. Ein doppelt so starkes Magnetfeld bedingt also eine doppelt so große Aufspaltung der Spektrallinien! Diese Aufspaltung der Spektrallinien ist aber selbst bei starken Magnetfeldern äußerst gering.

Berechnen wir hierfür einmal die unterschiedlichen potenziellen Energien:

Die Photonen des sichtbaren Lichts besitzen eine Energie von rund 2.5 eV. Die Zeemanaufspaltung beträgt hingegen nur etwa 60 µeV, sie ist also extrem gering.

Hierzu ein konkretes Beispiel: Ein Elektron fällt im Termschema um 2.5 eV nach unten und emittiert dabei Licht folgender Wellenlänge: Durch die Zeemanaufspaltung besitzt nun das Photon folgende Wellenlänge:

Eine solch geringe Aufspaltung der Emissionslinien kann mit einem gewöhnlichen Spektroskop nicht aufgelöst werden. Selbst die Natrium-D-Linien mit ihren 0.6 nm Abstand sind schon für etliche Spektroskope eine Herausforderung.

Abhilfe schafft hier ein spezielles Interferometer, das sog. Fabry-Perot-Interferometer. Mit diesem lassen sich selbst so geringe Wellenlängenverschiebungen wie beim Zeeman-Effekt erfassen.

---

Experiment 1:

Wie zum Schluss dieses Exkurses erwähnt lässt sich der Zeeman-Effekt spektroskopisch nur äußerst schwer nachweisen. Mit einem sog. Fabry-Perot-Interferometer, welches ich bereits gebaut habe (https://stoppi-homemade-physics.de/fabry-perot-interferometer/), ist dies aber unter Umständen, abhängig von der Finesse und dem erzielten Magnetfeld möglich.

Bildquelle: https://de.wikipedia.org/wiki/Helium-Neon-Laser#/media/Datei:He-Ne-Laser-Energieschema.svg

 

Als Laser kommt ein Helium-Neon-Laser mit λ = 632.8 nm zum Einsatz. Diesen konnte ich für nur 20 Euro günstig gebraucht erwerben.

Der Laser muss ja zur Beobachtung des Zeeman-Effekts in ein Magnetfeld mit der magnetischen Flussdichte B gebracht werden. Hierfür werde ich den HeNe-Laser mit Draht umwickeln und durch diesen dann Strom leiten. Ich hoffe, dass dann damit im Interfernzmuster der Fabry-Perot-Interferometers eine leichte Veränderung zu beobachten ist.

So, der Uniphase 1 mW Laser ist nach rund 1.5 Monaten doch noch bei mir angekommen. Hatte eigentlich nicht mehr damit gerechnet. Das Netzteil besitzt einen 4-poligen Anschluss mit den Farben Rot (Vcc), Schwarz (GND), Gelb (inable) und Weiß (?). Verbinde ich das gelbe Kabel mit der Versorgungsspannung und regle diese schön langsam hoch, beginnt der Laser bei rund 9 V/0.55 A zu leuchten. Je höher die Spannung (getestet bis 19 V), desto geringer wird die Stromstärke (sinkt auf 0.4 A). Ich werde ihn mit ca. 15 V betreiben und hoffe, damit auf der sicheren Seite zu sein.

Besonders froh bin ich über die geringe Größe des Lasers. Damit geht das Umwickeln mit der Spule hoffentlich leichter. Welches Kabel ich für den Elektromagnet verwende, weiß ich noch nicht genau. Ein Netzteil mit 0-30 V/30 A steht mir zur Verfügung…

Inzwischen habe ich den Helium-Neon-Laser mit 25 Meter 0.5 mm² Kabel in fast 5 Lagen umwickelt. Die Länge des Lasers beträgt 10 cm. Zur Abschätzung habe ich einmal den zu erwarteten Zeeman-Effekt ausgerechnet:

Nach diesem Ergebnis werde ich den Zeemaneffekt mit diesen Elektromagneten mit Sicherheit nicht feststellen können. Aber ich probiere es natürlich trotzdem…

Wenn mein Versuch (wie zu erwarten ist) scheitert, werde ich es mit Ferrit-Ringmagneten probieren. Dazu würde ich 7 Stück dieser großen Magnete benötigen:

Ich müsste mir dann eine mechanische Vorrichtung basteln, die den 10 cm langen Ringmagneten ohne Erschütterungen über den Laser stülpt. Mal schauen, ob ich das hinbekomme.

Für die experimentelle Bestimmung der spezifischen Elektronenladung e/m habe ich u.a. auch einen Ringmagneten verwendet.

Mit einem einzelnen Magneten erzielte ich eine Flussdichte im Inneren von 50 mT. Da kommt durch die benachbarten Magnete aber sicher noch etwas dazu. Bei geschätzten 90 mT habe ich aber leider auch nur die 3-fache Magnetfeldstärke im Vergleich zum obigen Elektromagneten und demnach eine zu erwartende effektive Wellenlängenverschiebung von nur 12 nm mit dem Fabry-Perot-Interferometer.

Mmmmh, ich befürchte dass diese Versuche zum Zeemaneffekt zum Scheitern verurteilt sind 🙁

Habe das Experiment heute mit dem umwickelten HeNe-Laser und dem Fabry-Perot-Interferometer durchführen können. Obwohl ich den Spulenstrom auf über 20 A gesteigert habe, konnte ich leider keinerlei Veränderungen des Interferogramms feststellen. Aber dies war wie oben schon rechnerisch gezeigt leider zu erwarten. Mein Interferometer hat leider eine viel zu geringe Auflösung/Finesse. Jetzt bleibt mir nur der Versuch mit der Natriumflamme im Magnetfeld, um den Zeemaneffekt nachweisen zu können.

Zumindest waren die Interferenzringe sehr gut zu sehen und sie reagierten auch sehr schön auf die Veränderung der Piezospannung und damit auf den Abstand der beiden Spiegel des Fabry-Perot-Interferometers.

 

Das Youtube-Video reiche ich noch nach…

---

Experiment 2:

Es gibt aber noch eine andere einfachere Methode, den Zeeman-Effekt experimentell nachzuweisen. Man benötigt hierfür eigentlich nur

• eine Natrium-Niederdrucklampe
• Magnesia-Stäbchen
• Kochsalz
• Bunsenbrenner
• einen starken Elektromagneten oder Permanentmagneten

Eine Natriumniederdrucklampe scheint auf einen Schirm und färbt diesen orange ein. Jetzt stellt man dazwischen einen Bunsenbrenner auf und zündet diesen. Es zeigt sich am Schirm noch keinerlei Veränderung. Hält man aber nun ein mit Kochsalz (NaCl) benetztes Magnesia-Stäbchen in die Flamme, so erkennt man am Schirm die dunkler erscheinende Flamme. Warum ist dies so?

Die Photonen der Natrium-Niederdrucklampe besitzen eine Wellenlänge von rund 589 nm. Diese Photonen treffen nun auf den Natriumdampf in der Flamme und werden in diesem absorbiert, da die Energie der Photonen genau mit jener notwendigen Energie im Natriumdampf für einen Sprung im Termschema nach oben übereinstimmt. Die angeregten Elektronen im Natriumdampf geben aber durch einen Sprung nach unten diese Energie in Form von Licht/Photonen gleich wieder ab. Diese Emission erfolgt aber nicht gerichtet, sondern in alle Richtungen mit der gleichen Wahrscheinlichkeit. Daher wird nur ein sehr geringer Teil der emittierten Photonen wieder in Richtung des Schirms abgestrahlt. Die meisten gehen in alle möglichen anderen Richtungen verloren. Daher fehlen am Schirm genau jene Photonen aus Richtung der Flamme und sie erscheint dunkel.

Was passiert aber nun, wenn man die Flamme einem starken Magnetfeld aussetzt?

Durch den Zeemaneffekt spalten nun die Energieniveaus der Natriumatome in der Flamme auf. Für einen Sprung nach oben (= Absorption) sind jetzt aber nicht mehr genau 589 nm notwendig! Daher regen die von der Natriumlampe kommenden Photonen die Elektronen im dem Magnetfeld ausgesetzten Natriumdampf nicht mehr an und werden daher nicht/weniger absorbiert. Sie fehlen dadurch aber auch nicht mehr auf ihrem Weg zum Schirm und die dunkle Flamme verschwindet. Durch das Magnetfeld wurden die Natriumabsorberatome quasi verstimmt.

Ich werde versuchen, diesen Versuch mittels starker Permanentmagnete umzusetzen und diese von den Seiten der gefärbten Flamme nähern. Die Natrium-Niederdrucklampe habe ich bereits. Der günstigste Weg an eine solche inkl. Drossel zu gelangen ist sich eine Osram Dunkelkammerlampe (z.B. Modell Studio 10) zu besorgen:

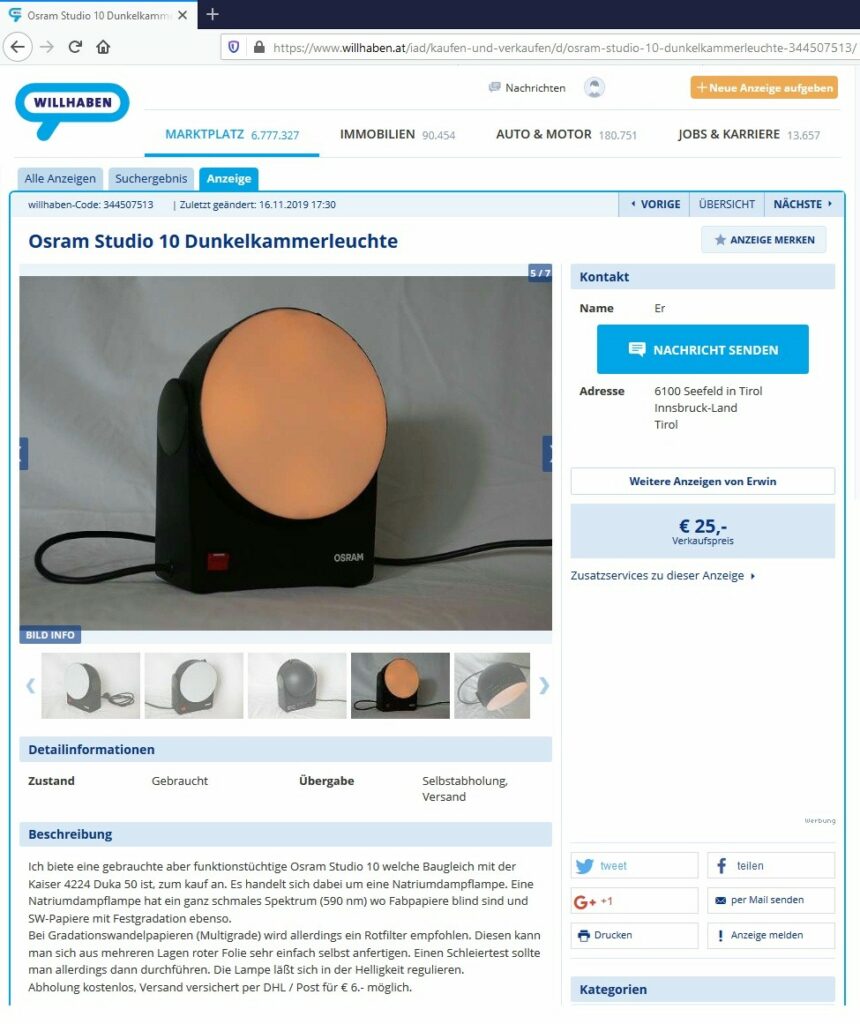
Da es sehr aufwendig ist einen Elektromagneten mit 1 T Flussdichte zu basteln, versuche ich es einmal mit Neodym Permanentmagneten. Dies hat allerdings den Nachteil, dass sich das Magnetfeld im Bereich der Flamme nicht einfach so ein- und ausschalten lässt. Die Permanentmagneten müssen erst zur Flamme verschoben werden bzw. dann wieder enfernt werden. Ich habe einmal diese 50 x 30 mm Magnete auf aliexpress bestellt. Sie sind mit nur rund 7 Euro pro Magnet unschlagbar günstig. Ich lasse mich überraschen, ob der Händler überhaupt liefert. Die beiden Scheibenmagnete werde ich mittels 4 Metallzylinder auf Abstand halten. 4 Stück deshalb, weil dann die Flamme keine der Halterungen erhitzt und man von der Seite trotzdem einen ungehinderten Blick auf die Flamme hat.

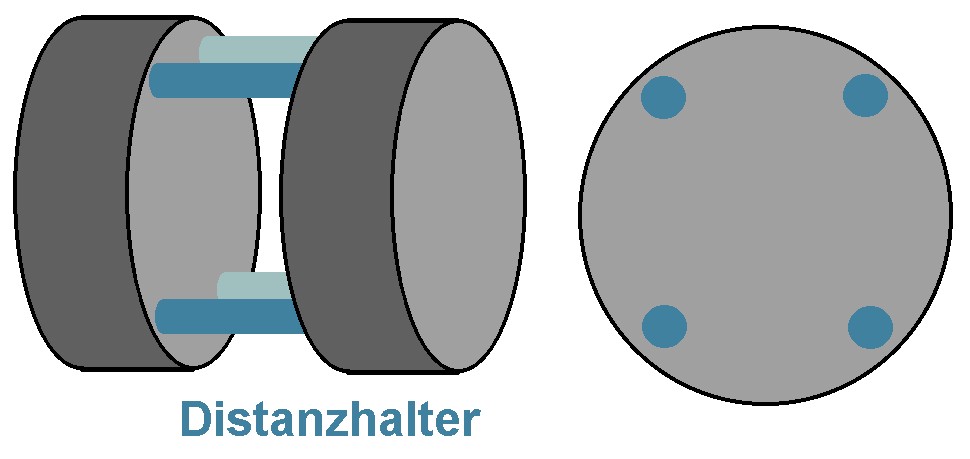
Als Bunsenbrenner werde ich diesen Gasbrenner fürs Flambieren missbrauchen. Er bietet die Möglichkeit, die Flamme auch ohne permanente Betätigung einer Taste brennen zu lassen.

Der Flambierbrenner ist heute angekommen. Jetzt muss ich bei einer Trafik einmal ein Feuerzeuggas besorgen.

Das Angebot für den Zylindermagneten auf aliexpress hat sich wie erwartet als Scheinangebot herausgestellt. Deshalb habe ich 2 Stück starker Neodymmagnete mit den Abmessungen 50 x 50 x 20 mm für insgesamt rund 40 Euro bestellt:

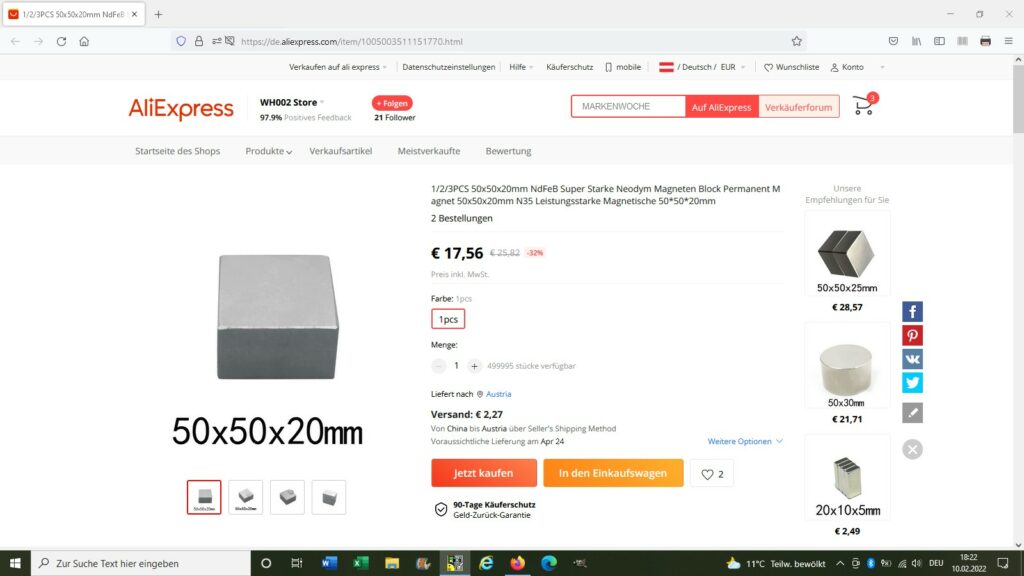
Die Magnesiastäbchen sind auch mittlerweile angekommen und ich konnte sie gleich mit dem Flambierbrenner und Kochsalz testen. Ergab eine schön orange Flamme: 

Hier nochmals ein Überblick über den gesamten Versuchsaufbau, so wie ich mir das vorgestellt habe:

Die beiden Magnete sind auch mittlerweile angekommen. Leider messen sie nur anstatt der angegebenen 50 x 50 x 20 mm nur 45 x 45 x 15 mm. Die Flussdichte im Zwischenraum ist zwar relativ schön homogen aber mit 0.15-0.2 T doch um einiges geringer als erwartet. Ob diese Stärke für einen beobachtbaren Zeeman-Effekt mit der Natriumflamme ausreicht ist fraglich…

Also die Resonanzabsorption mit der Natriumflamme im Licht der Natriumdampflampe funktioniert recht gut. Man sieht schön an der Wand den Schattenwurf der Flamme:

Der Versuch mit den beiden Permanentmagneten war leider nicht erfolgreich. Ich konnte wenn überhaupt nur minimale Veränderungen des Schattens im Magnetfeld beobachten. Ob diese dann überhaupt aufgrund des Zeemaneffekts zustandekamen oder eine andere Ursache hatten, kann ich nicht sagen. Das Magnetfeld mit nur rund 0.15 T im Zwischenraum ist wohl einfach deutlich zu schwach. Zudem kann man bei Verwendung von Permanentmagneten den Effekt nicht abrupt ein- und ausschalten, wie dies mit einem Elektromagneten möglich wäre.

Man erkennt nicht wirklich einen Unterschied des Schattens jener Flammenorte, welche sich im Magnetfeld befinden bzw. außerhalb liegen.

Hier gibt es ein exzellentes Video mit der erfolgreichen Visualisierung des Zeeman-Effekts mittels Natriumflamme: https://www.youtube.com/watch?v=iyBjPiRlxzg

Der Autor verwendet im Gegensatz zu mir einen wirklich massiven Elektromagnet. Ich habe ihn einmal gefragt, welche Flussdichte dieser im Zwischenraum liefert, wohl mehr als 1.5 T…

Auch mit einzelnen Magneten, welche ich in die Nähe der Flamme gehalten habe, erzielte ich keine sichtbare Veränderung des Schattens. Die Flussdichte direkt auf der Oberfläche der Würfelmagnete betrug 0.5 T. In einigen Millimetern Abstand sank dieser Wert aber auf 0.2 T, sodass die Flamme erst recht wieder nicht von einem ausreichend starken Magnetfeld durchsetzt wird.

---

Einen weiteren Versuch mittels Natriumflamme möchte ich noch starten aber diesmal mit einem Elektromagneten. Ich habe mir daher einen sehr großen Ferritring (120 x 80 x 20 mm) besorgt. Diesen werde ich mit 0.6 mm Kupferlackdraht bewickeln und dann einen Luftspalt aussägen. Die Enden werde ich dann konisch zusammenlaufen lassen in der Hoffnung, so die Flussdichte erhöhen zu können.

Hier eine kurze Überschlagsrechnung um die für B = 0.5 T notwendige Stromstärke abzuschätzen:

So, die Wickelarbeit ist beendet, jetzt geht es dann ans Zersägen…

Zum Aufschneiden des Ferritrings habe ich mir Diamant-Trennscheiben für meinen Dremel besorgt. Damit konnte der Ferritring überraschend gut bearbeitet werden. Leider haben die Trennscheiben nur einen Durchmesser von 22 mm, sodass ich keine durchgehenden, schönen Schnitten machen konnte und ich den Dremel oft nur schräg ansetzen konnte.

Mit meinem Hallsensor habe ich dann das Magnetfeld in Abhängigkeit von der Stromstärke bestimmt.

Bei 5 V und einer Stromstärke von 3.3 A erziele ich eine Flussdichte von 0.07 T. Ich werde daher die Spule mit meinem 30V/30A Netzteil betreiben, in der Hoffnung, dass die Spule Pulsströme um die 15 A verträgt. Dann sollte ohne einsetzende Sättigung die Flussdichte ca. 0.35 T betragen. Ich hoffe, dass dies dann für einen sichtbaren Effekt der Natriumflamme ausreicht, mal schauen…

Jetzt habe ich, weil ich neugierig war, die Spule an das leistungsstärkere Netzteil gehängt. Leider flacht die Kurve B = B(I) mit steigender Stromstärke (aufgrund der Sättigung) sehr stark ab und ich erhalte bei 31 V und 19 A lediglich 0.12 T. 🙁

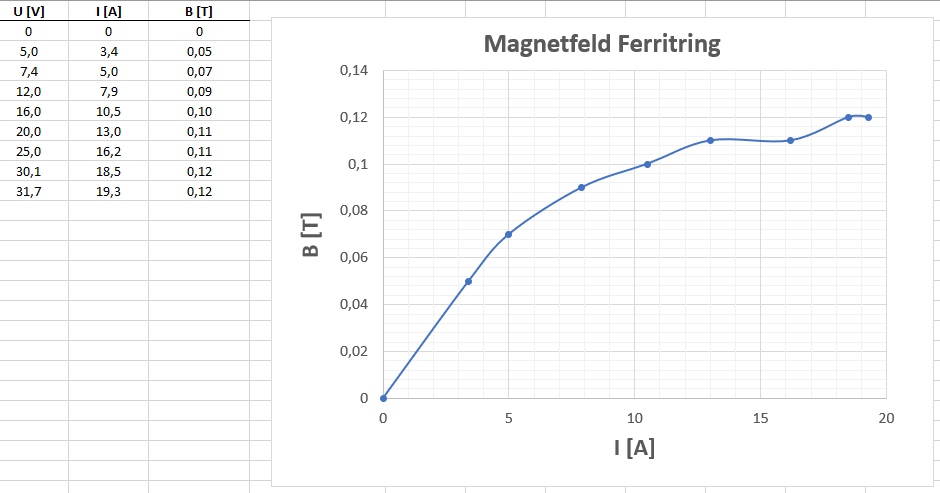
Damit kann ich mir die Nachweisbarkeit des Zeemaneffekts mit 100%iger Sicherheit abschminken, aber probieren werde ich es natürlich. Der Ferritkern ist für dieses Magnetfeld trotz seiner beachtlichen Abmessungen noch immer deutlich zu klein. Ob ich mir einmal einen noch viel größeren Elektromagneten baue, ist fraglich.

Wie zu erwarten war, kann ich keine Veränderung des Schattens der Natriumflamme bei Aktivierung des Magnetfelds beobachten. Damit sind wohl meine Versuche, den Zeemaneffekt zu erfassen, beendet bzw. gescheitert. Aber auch ein negatives Ergebnis ist ein Ergebnis. Vielleicht läuft mir ja in der Zukunft ein geeigneter, großer Trafo vor die Füße und ich kann meine Versuche fortsetzen. Vorerst war es das aber einmal zum Thema Zeemaneffekt….

So ganz losgelassen hat mich der unvollendete Zeeman-Versuch ehrlich gesagt nicht. Ich schaute mich immer wieder einmal auf ebay oder willhaben nach einem starken Schultransformator um. Dieser Tage wurde ich dann auf willhaben tatsächlich fündig. Ein großes und zudem noch sehr günstiges Schulexemplar genau nach meinem Geschmack. Das Joch werde ich mit Säge oder Flex bearbeiten, damit ich zulaufende Polschuhe erhalte. Ich hoffe, die Schenkel haben zumindest einen Querschnitt von 30×30 mm. Genaueres kann ich aber erst sagen, wenn er angekommen ist.

Der Transformator ist schon vor einiger Zeit bei mir angekommen. Zuerst habe ich ja versucht, aus dem Joch zwei zulaufende Polschuhe zu sägen. Dies verlief leider nicht erfolgreich. Daher habe ich die Polschuhe bei einer Spenglerei in Auftrag gegeben, welche mir diese gefräst haben. Heute konnte ich sie endlich abholen. Sie schauen sehr gut aus, waren mit 80 Euro aber auch nicht gerade billig. Die beiden Bügel zur Fixierung der Polschuhe habe ich mir selbst gebastelt.

Den Elektromagneten musste ich natürlich gleich testen und so nahm ich eine Messreihe (Flussdichte B in Abhängigkeit von der Stromstärke I durch die Spule mit 600 Windungen) auf. Bei einer Stromstärke von 3.56 A (angegeben sind I_max = 2 A) erziele ich im Luftspalt zwischen den beiden Polschuhen eine Flussdichte von immerhin 0.24 T. Dem Graph B = B(I) nach tritt auch noch keine Sättigung ein.

Da dies aber vermutlich für den Nachweis des Zeemaneffekts noch immer zu wenig ist, habe ich eine 3D-gedruckte Spulenhalterung für eine zweite Spule in Auftrag gegeben. Damit hoffe ich die Flussdichte deutlich zu erhöhen bzw. zu verdoppeln. Als Draht werde ich 0.6 mm Kupferlackdraht verwenden, den habe ich zuhause lagernd.

So, die Spulenhalterungen sind angekommen und passen perfekt. Jetzt muss ich sie nur noch bewickeln.

So, die 600 Windungen mit dem 0.6 mm Kupferlackdraht sind aufgebracht:

Hier nun die Messreihe B(I), also die Flussdichte B in Abhängigkeit von der Stromstärke I. Dabei habe ich beide Spulen parallel an mein 32V/30A Netzteil angeschlossen. Wie man erkennt, flacht die Kurve doch deutlich ab und der Kern sättigt. Bei einer maximalen Spannung von 31.7 V beträgt die Stromstärke immerhin 15.4 A. Die zugeführte elektrische Leistung beträgt dann beachtliche 488 W und die Flussdichte 0.44 T. Damit bin ich eigentlich zufrieden und ich kann den Versuch zum Zeemaneffekt neuerlich in Angriff nehmen.

So, heute versuchte ich den Zeemaneffekt mit dem Elektromagneten nachzuweisen und es gelang mir. Die Aufhellung des Schattens der Natriumflamme bei eingeschalteten Magnetfeld ist allerdings sehr gering und dies trotz der 0.45 T Flussdichte zwischen den Polschuhen. Aber ich bin sehr zufrieden mit dem Ergebnis, gelang es mir doch schlussendlich nach mehreren Anläufen den Zeemaneffekt nachzuweisen. Gekostet hat mich der Trafo 15 Euro, dann kamen noch die Polschuhe um 80 Euro dazu, die 3D-gedruckte Spulenhalterung um 10 Euro, der Kupferlackdraht um 10 Euro, die Natriumdampflampe um 30 Euro, die Magnesiastäbchen um 15 Euro und der Gasbrenner um 10 Euro, also insgesamt 170 Euro ohne 30V/30A Netzteil.

Hier das Video davon. Man muss aber schon recht genau schauen, um die geringe Aufhellung des Flammenschattens zu sehen:

 

Zum Abschluss noch das Youtube-Video: