Der Nobelpreis für Physik 2018 ging unter anderem an Arthur Ashkin für die Erfindung der optischen Pinzette. Dabei handelt es sich um eine Methode, Bakterien, Viren und selbst Atome mittels Laserstrahlen zu manipulieren.
Mein Versuch zur Laserlevitation entspricht vom Prinzip her einer solchen optischen Pinzette. Welche Physik steckt nun dahinter? In meinem Beitrag Elektronenbeugung (https://stoppi-homemade-physics.de/elektronenbeugung/) habe ich die berühmte Beziehung λ = h/p von Louis de Broglie bereits vorgestellt. Sie verknüpft auf einfache Art und Weise eine typische Teilcheneigenschaft, nämlich den Impuls p, mit einer typischen Welleneigenschaft, der Wellenlänge λ. Wie wir gesehen haben, verhalten sich beschleunigte Elektronen wie Wellen mit einer der de Broglie Beziehung entsprechenden Wellenlänge. Aber geht dies auch umgekehrt, sprich kann eine typische Welle auch eine Teilcheneigenschaft wie den Impuls p besitzen?
Licht gilt ja als eine elektromagnetische Welle, der man eine bestimmte Wellenlänge zuordnen kann. Für sichtbares Licht liegt diese Wellenlänge λ im Bereich zwischen [400,700] nm. Setzt man dies in obige Beziehung von de Broglie ein, so kann man Licht auch einen Impuls p zuordnen. Dieser ist umso größer, je kleiner die Wellenlänge ist. Dies deckt sich auch mit der berühmten Formel E = h·f für die Energie der Lichtteilchen. Mittels der Wellengleichung c = λ·f und der Beziehung p = h/λ folgt daraus:
p = h/λ = h/(c/f) = h·f/c = E/c
Steigende Energie des Lichtteilchens (sog. Photon) bedingt also auch einen höheren Impuls p. Dies würde der Logik nicht widersprechen. Max Planck nahm eben diese berühmte Quantisierung der Lichtenergie in lauter Portionen h·f vor, was wiederum für den Teilchencharakter von Licht sprechen würde.
Konzentrieren wir uns hier aber auf den Impuls der Photonen. Es gilt ja der sog. Impulserhaltumgssatz, welcher besagt, dass der Gesamtimpuls eines mechanisch abgeschlossenen Systems konstant ist. „Mechanisch abgeschlossenes System“ bedeutet, dass das System nicht in Wechselwirkung mit seiner Umgebung steht.
Nehmen wir als Beispiel einen Sportschützen. Vor dem Schuss beträgt der Gesamtimpuls des Systems Schütze-Gewehr-Patrone durch v = 0 ebenso 0. Nach Auslösen des Schusses bewegt sich die Patrone mit großer Geschwindigkeit in eine Richtung. Sie hat also einen bestimmten Impuls p. Da der Gesamtimpuls aber nach wie vor 0 sein muss, muss der Schütze einen in die Gegenrichtung gerichteten Impuls besitzen. Dies ist auch der Fall und man nennt dieses Phänomen auch Rückstoß. Dasselbe gilt für eine Rakete, welche den Treibstoff nach hinten ausstößt und dafür einen Impuls nach vorne erhält.

Impulserhaltungssatz und 3-tes Newtonsches Axion (actio = reactio bzw. Kraft = Gegenkraft) drücken eigentlich das gleiche aus, wenn man sich vor Augen hält, das die Kraft die Änderung des Impulses pro Sekunde ist.
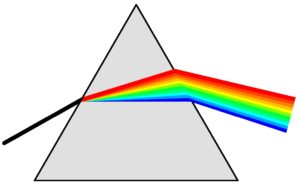
Was hat dies aber zum Beispiel mit der Lichtbrechung in einem Prisma oder einer Diamantkugel zu tun? Nun, durch die Lichtbrechung verändert sich die Ausbreitungsrichtung der Photonen und damit einhergehend verändert sich auch ihr vektorieller Impuls. Sie erhalten also in eine bestimmte Richtung einen Impuls p, den sie vor der Brechung noch nicht hatten. Dem Impulserhaltungssatz zufolge muss aber das die Impulsänderung verursachende Medium einen Gegenimpuls in die andere Richtung erhalten. Das Prisma bzw. die Diamantkugel erhält also durch die Lichtbrechung einen Impuls p. Warum verschiebt sich dann aber das Prisma nicht?
Laut der Formel von de Broglie besitzt Licht der Wellenlänge λ einen Impuls p = h/λ. Die Wellenlänge λ liegt im Bereich von 10^-7 m, das Plancksche Wirkungsquantum bei 10^-34. Demnach besitzt ein Photon im sichtbaren Spektralbereich einen Impuls von nur 10^-27 kg·m/s. Auch wenn Milliarden von Photonen pro Sekunde durch das Prisma abgelenkt werden, reicht dies noch lange nicht aus, dieses in Bewegung zu versetzen.
Was ist aber, wenn das lichtablenkende Objekt selbst sehr klein und leicht ist? Dann könnte es sehr wohl durch Lichtablenkung bewegt werden. Genau diesen Umstand macht man sich bei der Laserlevitation zunutze.
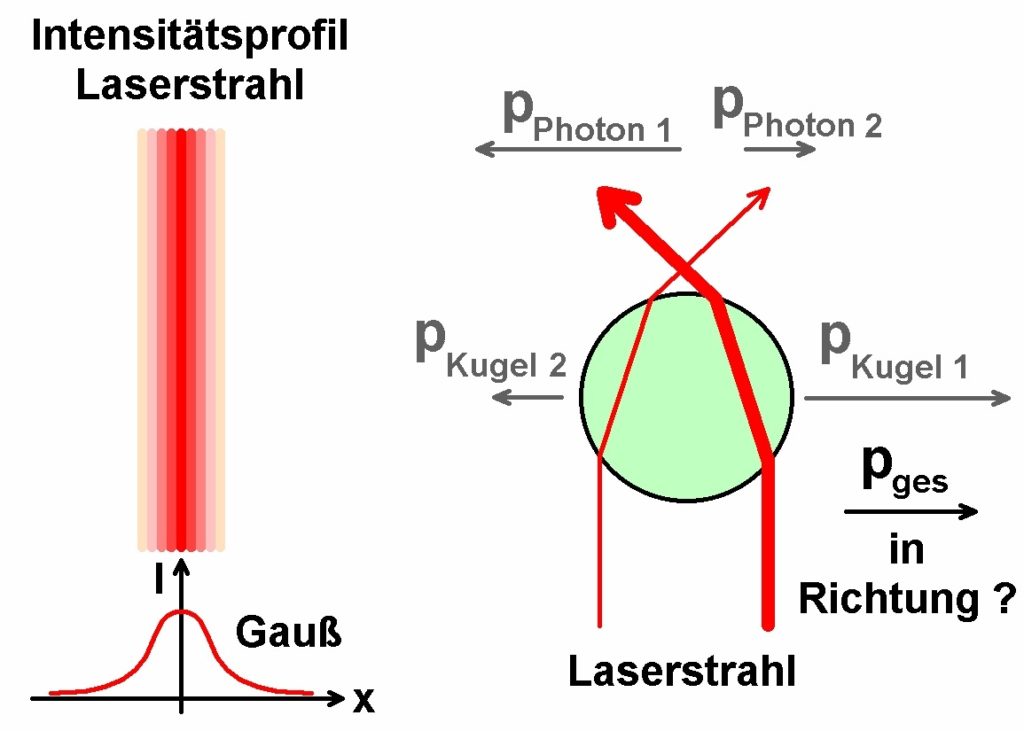
Als lichtbrechendes Objekt wählte ich synthetische Diamanten mit einem Durchmesser von ca. 0.1 µm. Bringt man die Diamanten in den Strahl eines starken Lasers (rund 150mW), so erfahren diese einen Impuls bzw. eine Kraft. Da aber der Laserstrahl an allen Stellen der Diamantkugel auftrifft, müssten sich die vielen Lichtablenkungen und demnach auch die übertragenen Impulse aufheben. Der Grund warum dies nicht der Fall ist liegt im Intensitätsprofil des Laserstrahls. Die Intensitätsverteilung gleicht einer Gaußschen Glockenkurve, sprich die Intensität ist in der Strahlmitte am stärksten und nimmt zu den Rändern hin ab.
Dies hat aber zur Folge, dass nicht überall gleich viele Photonen abgelenkt werden. In Richtung Laserstrahlmitte werden mehr Photonen in die Gegenrichtung abgelenkt als in Richtung Strahlrand. Demnach ist der Impulsübertrag auf die Diamantkugel auch unsymmetrisch. Es kommt zu einem stärkeren Impulsübertrag in Richtung Laserstrahlmitte. Dies hat aber einen stabilisierenden Effekt auf die Laserkugel. Entfernt sie sich etwa von der Strahlmitte, wird sie durch dieses Ungleichgewicht wieder zur Strahlmitte gedrängt. Die Lasermikrokugel sollte also im Strahl gefangen bleiben.
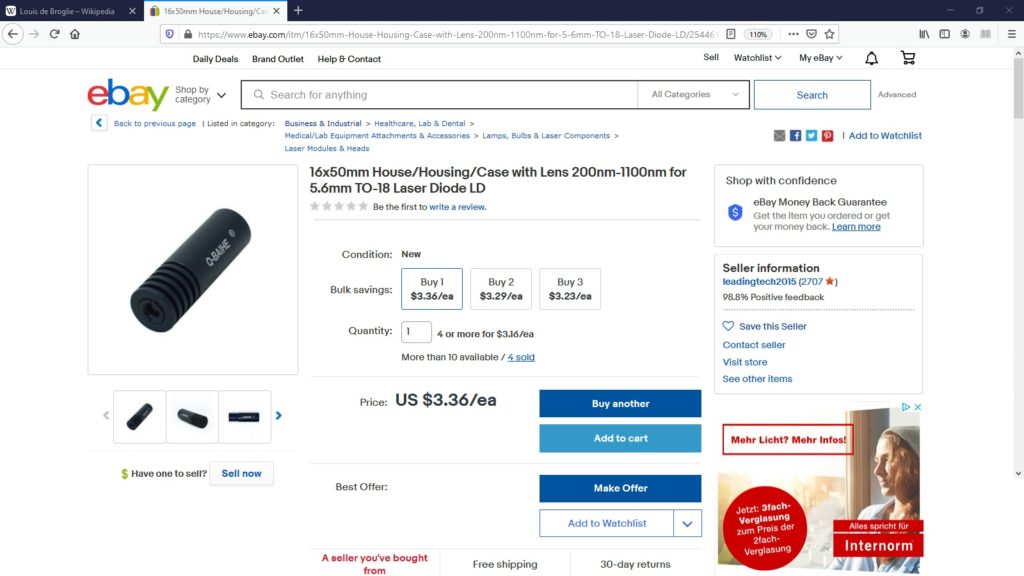
Genau diesen Effekt habe ich experimentell nachgestellt. Als lichtablenkendes Objekt kommen wie schon gesagt sehr kleine synthetische Diamantkugeln zum Einsatz. Diese konnte ich um ca. 20 Euro über Amazon aus den USA beziehen. Den starken Laser bastelte ich mir aus einen alten DVD-Laufwerk. Wichtig ist es bei diesem Versuch auch, den Laserstrahl knapp nach seiner Austrittslinse zu fokusieren. Auf ebay gibt es dafür günstige Sets für Laserdioden bestehend aus einem zylinderförmigen Kühlkörper plus Fokusierlinse.
Damit dieser Versuch gelingt, bedarf es ein wenig Geschick. Auch dürfen keine störenden Luftströmungen vorhanden sein, welche die Mikrokugeln sonst sehr schnell aus dem Laserstrahl befördern würden.