
Zufallsschaltungen sind elektronische Schaltungen, bei denen man den Ausgang innerhalb bestimmter Grenzen (z.B. Zahlen/Augen 1 bis 6) nicht vorhersagen kann. Wie schon angedeutet wäre ein elektronischer Würfel ein Beispiel für eine solche Zufallsschaltung. Ich habe hier einige unterschiedliche Schaltungen zusammengetragen.
Elektronischer Würfel







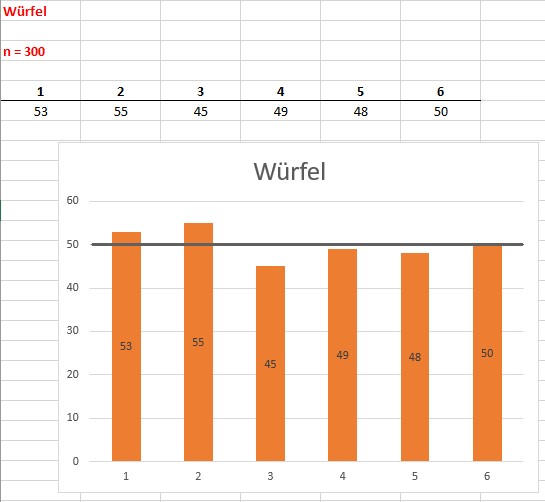
Mit dieser Schaltung könnte man u.a. das Gesetz der großen Zahlen überprüfen, wonach sich die relative Häufigkeit h für ein bestimmtes Ereignis für eine große Anzahl an Wiederholungen der Wahrscheinlichkeit p nähert. Wiederholt man z.B. den einmaligen Würfelwurf sehr oft, so strebt die relative Häufigkeit für die Augenzahl 4 gegen p = 1/6.

Experiment mit 300 Würfen:
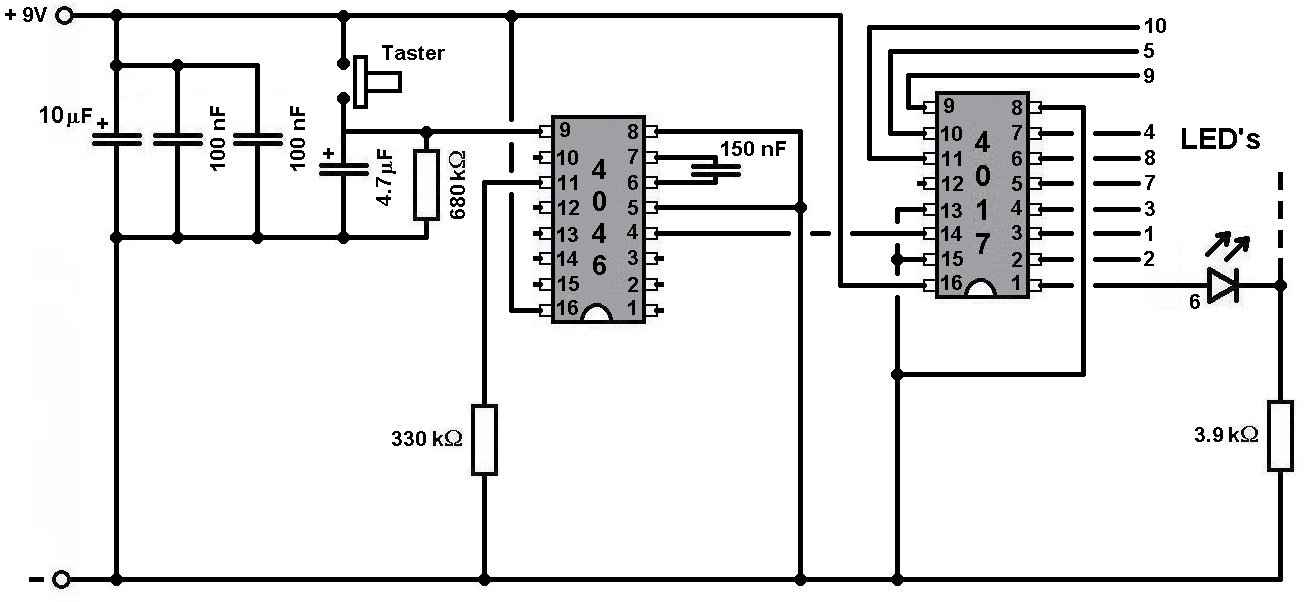
Roulette
Auch diese Schaltung benötigt unter anderem den IC CD4017, einen sog. Dekadenzähler.





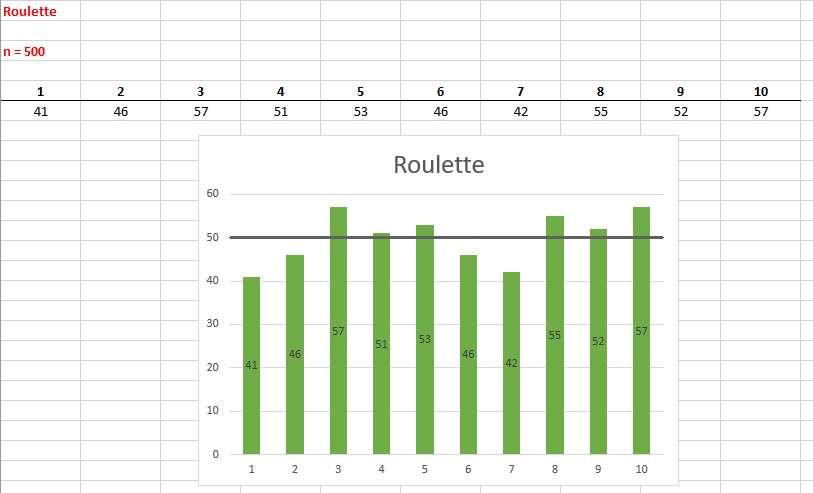
Experiment mit 500 Durchläufen:
Kopf oder Zahl – Münzwurf
Bei dieser Zufallsschaltung gibt es wie beim Münzwurf nur zwei Ausgänge, Kopf oder Zahl. Gefunden habe ich die Schaltung im Buch „Getting started in electronics“ von Forrest Mims, einen US-amerikanischen „Bastler“ ähnlich verrückt wie ich 😉
Der 4-fach NAND-Gatter IC CD4011 fungiert hier als flip-flop…




Experiment mit 200 Würfen:

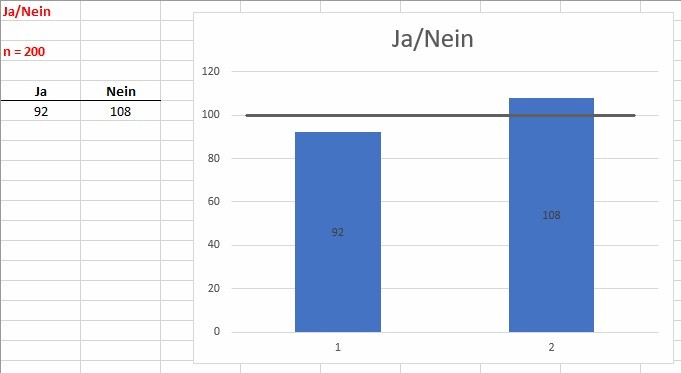
Entscheidungshelfer – Ja/Nein
Auch diese einfache Schaltung liefert zwei unterschiedliche Ausgänge Ja bzw. Nein und kann einem somit lästige Entscheidungen per Zufall abnehmen.
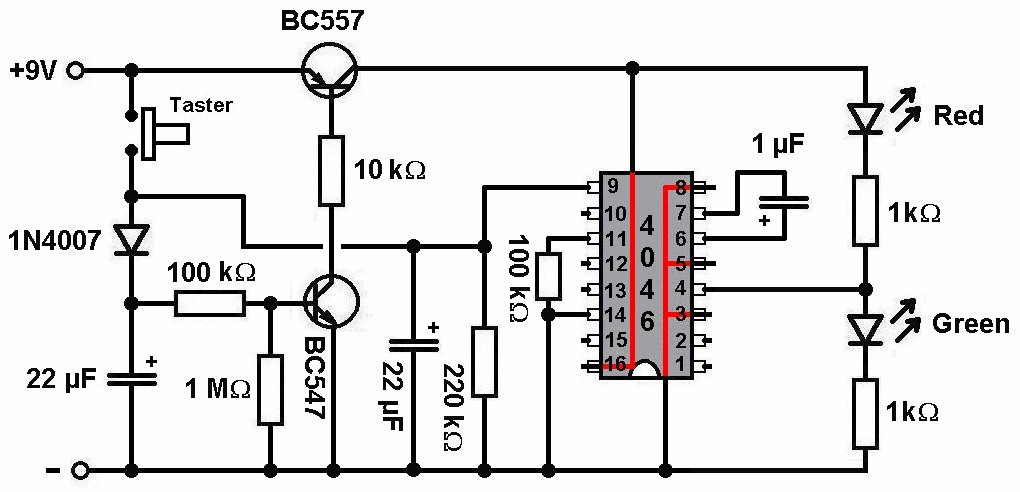


Drückt man den Taster, so blinken zunächst die beiden LEDs abwechselnd sehr schnell. Danach nimmt die Frequenz kontinuierlich ab bis zum Schluss nur noch eine LED aufleuchtet. Die grüne LED kann dann für ein Ja, die rote für ein Nein stehen 😉
Diese einfache Schaltung eignet sich meiner Meinung nach bestens für das Physiklabor in der Schule bzw. den Mathematikunterricht zum Thema Wahrscheinlichkeit. Man kann damit zum Beispiel auch das Gesetz der großen Zahlen überprüfen (siehe unten).
Experiment mit 200 Wiederholungen:
Auch mit dem Arduino und der Funktion random( ) lassen sich beliebige „Zufallsschaltungen“ realisieren.
Quelle: https://www.arduino.cc/reference/en/language/functions/random-numbers/random/
Hier ein extrem einfaches Programm zur Simulation des Münzwurfs:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
int n, Treffer; void setup() { Serial.begin(9600); Treffer = 0; n = 0; } void loop() { n++; if(random(2) == 1) { Treffer++; } Serial.print(n); Serial.print(": "); Serial.print(Treffer); Serial.print(" rel. Haeufigkeit: "); Serial.println(1.0 * Treffer/n); delay(500); } |
Trägt man die relative Häufigkeit für z.B. „Kopf“ gegen die Anzahl der Würfe auf, so erkennt man das „Gesetz der großen Zahlen„, indem die relative Häufigkeit h mit zunehmender Anzahl an Würfen immer näher zur tatsächlichen Wahrscheinlichkeit p (in diesem Fall p = 1/2) rückt.

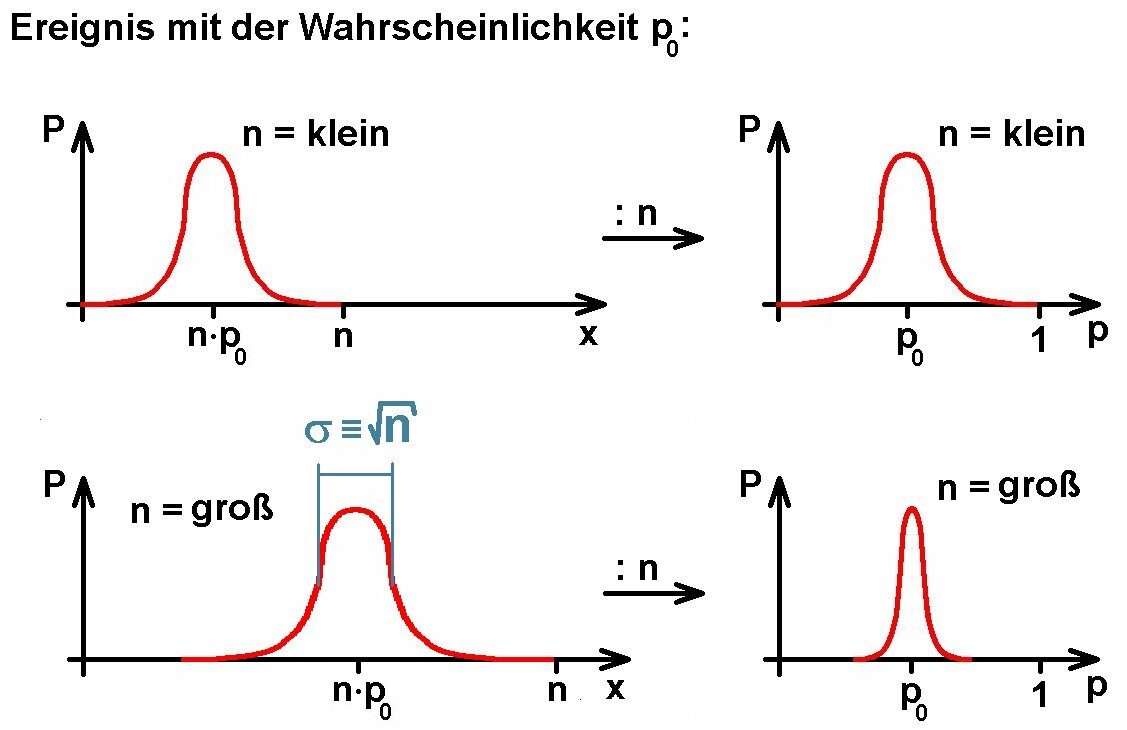
Der Grund ist folgender: Bei n Würfen und der Wahrscheinlichkeit p0 erhält man eine Verteilung mit dem Erwartungswert n · p0 und der Standardabweichung √[n · p0 · (1 – p0)]. Die Verteilung rückt also mit zunehmendem Umfang n weiter nach rechts und wird auch breiter. Allerdings wird sie nur um den Faktor √n breiter und nicht um das n-fache. Geht man nun von P(x) zu der Wahrscheinlichkeitsverteilung P(p) über, so muss man die x-Werte durch n dividieren. Man erhält dann eine Verteilung um den Erwartungswert n · p0 / n = p0 und mit der Breite √n / n = 1 / √n.
Wie man erkennen kann, nimmt die Breite der Verteilung P(p) mit zunehmenden n durch den Ausdruck 1 / √n immer mehr ab, sprich sie wird schmäler um den Wert p0 herum. Was bedeutet dies? Nun, bei sehr vielen Wiederholungen n erhält man nahezu ausschließlich nur noch relative Häufigkeiten/Wahrscheinlichkeiten nahe bei der tatsächlichen Wahrscheinlichkeit p0. Dies ist das Gesetz der großen Zahlen…
Konkretes Beispiel: Würfel ich zum Beispiel n = 6 mal mit einem Würfel, so erhalte ich eine breite (!) Verteilung um den p-Erwartungswert 1/6 für einen „6-er“. Das heißt, es werden auch die relativen Häufigkeiten 0/6, 2/6 usw. häufiger vorkommen, denn es kann gut sein, dass man bei nur 6 Würfen zufälligerweise auch z.B. 3mal einen 6-er würfelt.
Würfel ich aber nun n = 6000 mal mit dem Würfel und bestimme die relative Häufigkeit für einen 6-er, so liegt diese aufgrund des Gesetzes der großen Zahlen nahezu immer ganz knapp bei 1/6, also bei 1000 mal einem 6-er. Es ist nahezu unmöglich zum Beispiel bei 6000 Würfen etwa 2000 mal einen 6-er zu erzielen. Die relative Häufigkeitsverteilung ist nämlich bei vielen Würfen ganz schmal (!) um den Erwartungswert 1/6! Deshalb strebt die relative Häufigkeit eines Ereignisses für viele Wiederholungen immer gegen die Wahrscheinlichkeit p0.
„Radioaktiver“ Zufallsgenerator



Man kann auch mit einem Geigerzähler eines sehr guten Zufallsgenerator basteln. Die Ausgabepulse werden an den Arduino weitergeleitet und dieser bestimmt den Zeitpunkt des Ereignisses mit dem Befehl millis(). Nach einer einstellbaren Zeit, zum Beispiel 1 Sekunde, betrachtet man den Zeitpunkt des letzten aufgetretenen Pulses. Ist dieser eine gerade Zahl so gibt der Zufallsgenerator eine 0 aus, bei einer ungeraden Zahl eine 1. Dies überprüft man mittels modulo (Restklassenmenge), konkret modulo 2 (%2).
Arduino-Code:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 |
#include <LiquidCrystal_I2C.h> #include <Wire.h> #include <SPI.h> LiquidCrystal_I2C lcd(0x27,16,2); // set the LCD address to 0x27 for a 16 chars and 2 line display. ACHTUNG: Adresse kann auch 0x3F sein !!! // Anschlüsse: // GND - GND // VCC - 5V // SDA - ANALOG Pin 4 // SCL - ANALOG pin 5 const byte interruptPin = 2; long time_last_pulse; bool random_value; int n_0,n_1; // =========================== // ======= SETUP ========= // =========================== void setup() { Serial.begin(9600); pinMode(interruptPin, INPUT); attachInterrupt(digitalPinToInterrupt(interruptPin), Puls, RISING); pinMode(LED_BUILTIN, OUTPUT); n_0 = 0; n_1 = 0; lcd.begin(); // initialize the lcd lcd.backlight(); lcd.setCursor(0,0); lcd.print("Geigerzaehler"); lcd.setCursor(0,1); lcd.print("Zufallsgenerator"); delay(3000); lcd.setCursor(0,0); lcd.print(" "); lcd.setCursor(0,1); lcd.print(" "); } // =========================== // ======= LOOP ========= // =========================== void loop() { delay(1000); // change time in milliseconds, after which you want to get a new random 0 or 1 value if(time_last_pulse % 2 == 0) // latest radioactive pulse-time is even { random_value = 0; digitalWrite(LED_BUILTIN, LOW); n_0 = n_0 + 1; } else // latest radioactive pulse-time is odd { random_value = 1; digitalWrite(LED_BUILTIN, HIGH); n_1 = n_1 + 1; } lcd.setCursor(0,0); lcd.print(" "); lcd.setCursor(0,0); lcd.print(random_value); lcd.print(" "); lcd.setCursor(0,1); lcd.print("0:"); lcd.print(n_0); lcd.print(" 1:"); lcd.print(n_1); lcd.print(" "); } // ============================== // ======= INTERRUPT ========= // ============================== void Puls() { time_last_pulse = millis(); } |
Möchte man zum Beispiel 10 Zufallsausgänge haben, muss man auf modulo 10 (%10) wechseln. Dann ist das Zufallsergebnis eine Zahl zwischen 0 und 9. Mit dem delay ändert man die zeitliche Ausgaberate der Zufallszahlen. Bei delay(1000) erhält man zum Beispiel konkret jede Sekunde eine neue Zufallszahl.


Mit zunehmender Messdauer ergaben sich dann folgende Ergebnisse:



Nach fast 6 Stunden Gepiepse mit sekündlicher Zufallszahl 0 oder 1 beendete ich dieses Experiment:


Hier die zeitliche Entwicklung der relativen Häufigkeiten für das Ereignis 0 bzw. 1. Man erkennt wunderbar, wie sich die relativen Häufigkeiten immer mehr der Wahrscheinlichenkeit p = 50% nähern, Heureka 😉

Zum Abschluß das Youtube-Video:

