Für die Verdrehung einer Blattspiralfeder um den Winkel φ benötigt man eine Kraft F bzw. ein Drehmoment T = F · l. Zwischen T und φ gilt die einfache Beziehung T = R · φ. Ein doppelt so großer Verdrehwinkel bedingt also ein doppelt so großes Drehmoment. Die Proportionalitätskonstante R zwischen T und φ nennt man Richtmoment. Dieses gibt das notwendige Drehmoment für die Verdrehung um φ = 1 rad ≈ 57.3° an. Eine schwer zu verdrehende Spiralfeder besitzt also ein großes Richtmoment und vice versa…

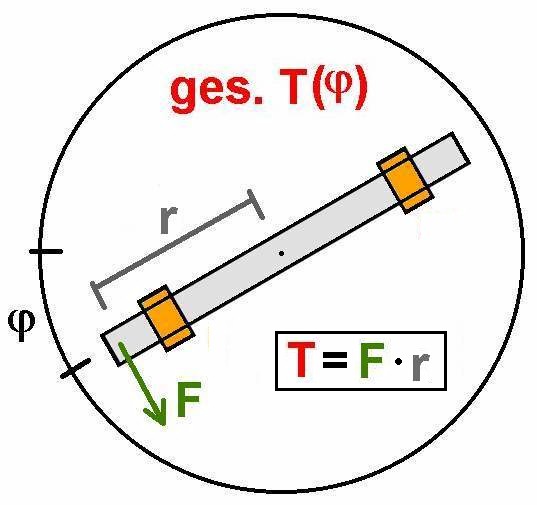
Trägt man das Drehmoment T gegen den Verdrehwinkel φ auf, so müsste man eine ansteigende Gerade erhalten mit der Steigung k = R:

Verdreht man die Spiralfeder und lässt sie wieder los, so beginnt diese zu schwingen. Die Periodendauer τ lässt sich wiefolgt herleiten:

Die Periodendauer τ ist also dann groß, wenn das Trägheitsmoment I des schwingenden Körpers groß ist und das Richtmoment R klein. Misst man die Periodendauer τ und kennt das Richtmoment R, so kann man das Trägheitsmoment I berechnen.Genau darum wird es in diesem Experiment gehen.
Die für den Versuch benötigten Teile habe ich weitestgehend auf Amazon gekauft:





Die schwingenden Massen sind in meinem Fall zwei auf einem 4 mm Alustab montierte Bleikugeln mit je 40 g Masse:

Als Drehachse kommt ein 8 mm Alustab zum Einsatz:

Für die Bestimmung des Richtmoments R benötige ich ja das bei einem Drehwinkel φ aufgebrachte Drehmoment T = F·l. Dieses ermittle ich mit einer Federwaage, welche ich noch bestellen muss. Ich habe mich gleich für ein Set bestehend aus 5 Federwaagen entschieden:
Nachdem heute der 8 mm Aluminiumstab angekommen ist, konnte ich den Aufbau fortsetzen.

Auf der Stirnseite der Achse musste ich ein M4-Gewinde schneiden, um dann die Gewichtsträgerachse mit einer Schraube fixieren zu können:



Mein günstiger Gewindeschneidersatz, den ich schon für viele Aufbauten benötigt habe:


Die Gewichtsträgerachse besteht aus einem 4 mm Aluminiumstab:


Die Bleikugeln musste ich mit einem 4.2 mm-Bohrer aufbohren…

Hier sieht man schön das in die Spiralfeder gebohrte Loch zur späteren Fixierung an der Pendelachse:


So schaut es während der Arbeit in meiner Küche aus… 😉




Heute habe ich den Aufbau finalisiert und dazu eine 20 x 20 cm Holzplatte ausgeschnitten:

Für die Bestimmung des Richtmoments R muss ich ja den Auslenkungswinkel φ kennen. Daher habe ich mir eine kreisförmige Winkelschablone ausgedruckt und auf die Holzplatte geklebt:




Die äußere Gegenhalterung der Spiralfeder habe ich mit einem Stuhlwinkel umgesetzt:


Hier nun mein fertiges Torsionspendel:

Die zum Einsatz kommenden Federwaagen von Amazon:

Konkret benötige ich die 1N-Federwaage:


Im ersten Experiment zum Torsionspendel wird das Richtmoment R bestimmt. Dazu muss man das Drehmoment T in Abhängigkeit vom Drehwinkel φ aufzeichnen.


Mittels einer hängenden Beilagscheibe konnte ich die Winkelposition des Trägerstabs relativ einfach bestimmen:


Zwischen dem Drehmoment T und dem Drehwinkel φ müsste eine direkte Proportionalität vorliegen mit dem Anstieg k = Richtmoment R:

Hier meine experimentellen Ergebnisse. Die Werte liegen recht schön auf einer ansteigenden Geraden, so wie es sein sollte:
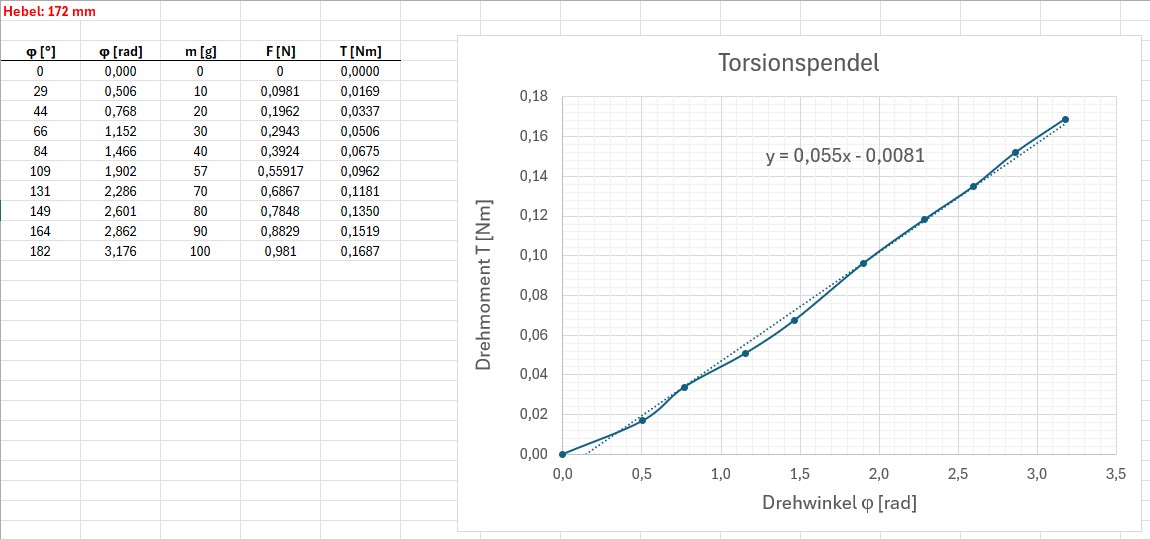
Der Anstieg k ist gleich 0.055 Nm pro Radiant was genau dem Wert des Richtmoments R entspricht. Unser Ergebnis des ersten Experiments lautet also:
Im zweiten Experiment wird aus der Periodendauer τ das Trägheitsmoment I bestimmt. Es gilt ja der Zusammenhang:

Kenne ich R und τ, so kann ich das Trägheitsmoment I ermitteln. Auf der Messingstange werden von mir symmetrisch zwei Bleikugeln (m = 37.18 g) im Abstand d zur Drehachse postiert und die Periodendauer ermittelt. Daraus errechnet sich dann das Gesamtträgheitsmoment Iges von Drehachse, Messingstab und Kugeln. Subtrahiert man von Iges nun I0 (= Trägheitsmoment ohne Kugeln), so erhält man das reine Trägheitsmoment der beiden Kugeln. Dieses müsste näherungsweise Ith = 2·m·d² sein. Zum Schluss vergleiche ich das experimentelle Ergebnis Iexp mit dem Theoriewert Ith.







Die Messergebnisse:


In den beiden letzten Spalten befinden sich die experimentell ermittelten bzw. theoretischen Trägheitsmomente der beiden Kugeln. Wie man sieht, stimmen sie eigentlich sehr gut überein, Heureka 😉

Zum Abschluss noch das Youtube-Video:
Satz von Steiner

Bildquelle: Wikipedia
Der Satz von Steiner ist nach dem Schweizer Mathematiker Jakob Steiner (1796 – 1863) benannt. Er hilft das Trägheitsmoment eines sich drehenden Körpers zu bestimmen. Das Gegenstück der Masse m bei der Translation ist das Trägheitsmoment I bei der Rotation. Das Trägheitsmoment einer Punktmasse m, welche im Normalabstand r zur Drehachse rotiert beträgt I = m · r².

Für einen ausgedehnten Körper muss man dann für das gesamte Trägheitsmoment die Summe über alle kleine Massestücke mal deren Abstand zum Quadrat bilden, also ∑ mi · ri². Mathematisch geschieht dies dann mittels Integralrechnung. Für die wichtigsten geometrischen Körper liegen die Ergebnisse für I bereits in Tabellen vor:

Quelle: Wikipedia
Aber was besagt nun der Satz von Steiner? Kennt man das Trägheitsmoment IS eines beliebigen Körpers um eine bestimmte Drehachse durch den Schwerpunkt S, so gilt für das Trägheitsmoment I um eine dazu parallele (!) Drehachse im Abstand a: I = IS + m · a².
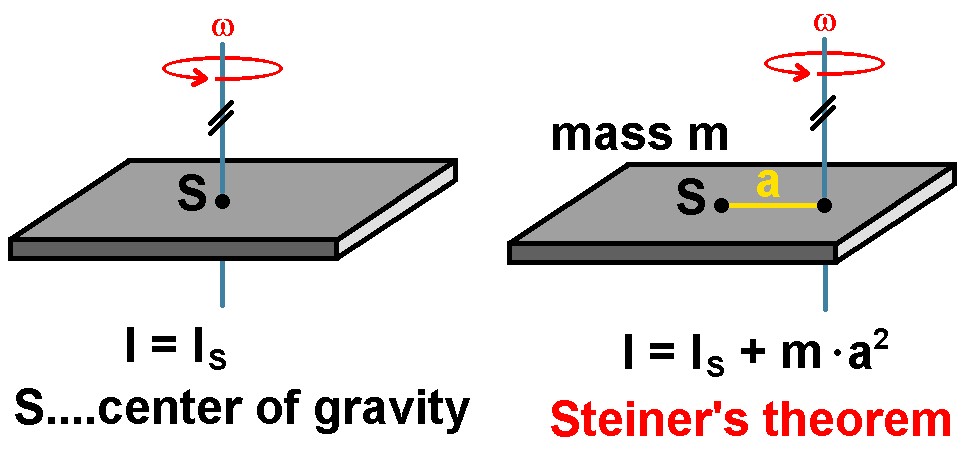
Genau diese Aussage möchte ich experimentell mittels Torsionspendel überprüfen. Dazu postiere ich eine Aluplatte auf dem Torsionspendel und bestimme über die Periodendauer der Schwingung das Trägheitsmoment in Abhängigkeit vom veränderten Abstand a.
In die Aluplatte bohrte ich vom Schwerpunkt S aus startend alle Zentimeter ein Loch:




Die Aluplatte fixierte ich sodann an den unterschiedlichen Löcherpositionen auf der Achse des Torsionspendels:



Hier betrug zum Beispiel der Abstand zum Schwerpunkt genau a = 3 cm:

Jetzt musste ich nur noch mit der Stoppuhr die Periodendauer τ in Abhängigkeit vom Abstand a bestimmen. Ich mittelte dabei immer genau 5 volle Schwingungen.


Aus den gemessenen Periodendauern τ und dem bekannten Richtmoment R des Torsionspendels (R = 0.055 Nm/rad, siehe weiter oben) lässt sich dann mittels der Formel

das jeweilige Trägheitsmoment I in Abhängigkeit von a ermitteln. Wir kennen aber nun durch den Satz von Steiner den theoretischen Zusammenhang zwischen I und dem Abstand a und zwar I = IS + m · a². Trägt man daher die experimentell ermittelten Trägheitsmomente I gegen das Quadrat a² der Abstände auf, so müssten die Werte auf einer steigenden Geraden liegen:

I entspricht dabei gemäß der Geradenformel y = k · x + d dann dem y-Wert, IS dem d, m dem k und a² dem x.

Und wirklich, meine Werte liegen annähernd auf einer Geraden, Heureka…
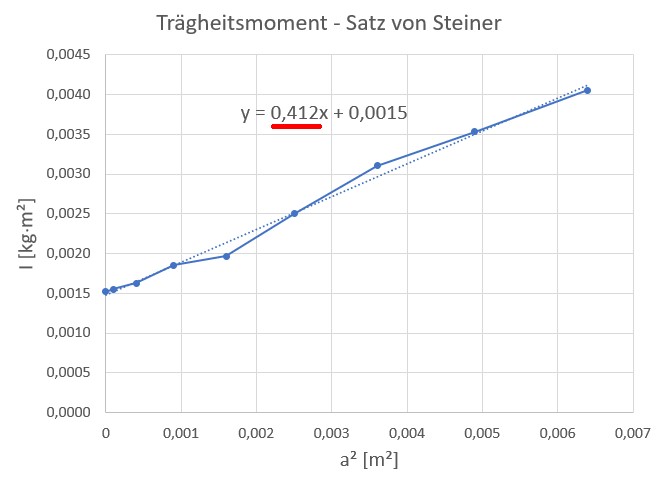
Der Anstieg k = 0.412 sollte exakt der Masse m der Aluplatte entsprechen. Um dies zu überprüfen, legte ich zum Schluß die Aluplatte auf eine Waage mit dem Ergebnis m = 0.382 kg.


Die Abweichung Experiment (0.412 kg) zu Theorie (0.382 kg) beträgt etwas weniger als 8%, damit kann ich absolut leben 😉

