In einem meiner Experimente (https://stoppi-homemade-physics.de/elektronenbeugung/) habe ich gezeigt, dass typische Teilchen wie Elektronen auch als Welle in Erscheinung treten können. Basis bildete die bekannte, auf den Physiker Louis de Broglie zurückgehende Verknüpfung von Impuls p (typische Teilcheneigenschaft) und Wellenlänge λ (typische Welleneigenschaft):

λ = h/p      h …. Plancksches Wirkungsquantum (= 6.63 · 10^ –34 Js)

Was ist aber nun mit Licht? Licht wurde im Laufe der Geschichte einmal mehr als Teilchen und dann wieder mehr als Welle aufgefasst. Als typische Welle tritt Licht etwa bei Beugungserscheinungen mit seinen konstruktiven und destruktiven Interferenzen auf. Andererseits haben wir gesehen, dass etwa zur Erklärung des Photoeffekts (https://stoppi-homemade-physics.de/photoeffekt/) Licht als Teilchen betrachtet werden muss. Heute wissen wir, dass Licht in beiderlei Formen auftreten kann und je nach Experiment bzw. Messung einmal mehr der Teilchencharakter oder eben der Wellencharakter in den Vordergrund tritt.

Wenn Licht aber auch als Strom vieler Teilchen (Photonen) gesehen werden kann, dann müsste man diese doch auch irgendwie einzeln detektieren können oder? Und in der Tat, einzelne Photonen lassen sich mit sog. Photomultipliern tatsächlich registrieren.

Bildquelle: https://de.wikipedia.org/wiki/Photomultiplier#/media/Datei:Photomultiplier_schema_de.png

Ein Photomultiplier ist eine Art Elektronenröhre mit einem Eintrittsfenster. Durch dieses treffen Lichtteilchen auf eine lichtempfindliche Schichte, die sog. Photokathode. Dort werden wie beim äußeren lichtelektrischen Effekt Elektronen freigesetzt. Durch eine Vielzahl von sog. Dynoden, welche unter Hochspannung stehen, werden diese Elektronen beschleunigt und ähnlich wie bei einer Lawine vervielfältigt. Dadurch erzeugen sie bei der Anode angekommen über einen Lastwiderstand einen kurzen Spannungspuls, welcher dann weiter verarbeitet oder einfach nur gezählt wird.

In diesem Experiment möchte ich Wellen- und Teilcheneigenschaften von Licht parallel zeigen. Einerseits liegt dem Versuch die Beugung am Gitter zugrunde und andererseits registriere und zähle ich die einzelnen Lichtteilchen.

Damit man einzelne Lichtteilchen zählen kann, benötigt man extreme Dunkelheit. Betrachten wir einen schwachen, grünen Laserpointer mit der Leistung von 5 mW und der Wellenlänge λ = 532 nm. Pro Sekunde emittiert dieser dann eine Energie E = P·t von genau 5 mJ. Ein einzelnes Photon besitzt nach der berühmten Gleichung E = h·f = h·c/λ von Max Planck die Energie

E = 6.63·10^–34 · 3·10^8 / 532·10^–9 = 3.74 · 10^–19 J

Daraus folgt, dass die gewaltige Anzahl von 1.34 · 10^16 = 13 400 000 000 000 000 Photonen pro Sekunde den Laserpointer verlassen. Man muss also den Laserstrahl um viele Zehnerpotenzen abschwächen. Genau dies leistet ein sogenannter Neutraldichtefilter (ND-Filter). Bei ihm wird immer der Schwächungsfaktor angegeben. Beträgt dieser ND 3, so schwächt er Licht um den Faktor 10^–3 = 1/1000 ab. Ist dieser Faktor hingegen nur 0.7, so gilt für die Abschwächung 10^–0.7 = 0.20 = 20%.

In meinem Versuch kommen 3 Lagen von Neutraldichtefiltern der Marke Kodak Wratten Nr. 96 mit ND 4 + eine weitere Lage mit ND 1 zum Einsatz. Die Gesamtabschwächung beträgt somit ND 13. Die Laserleistung wird dadurch um den Faktor 1/10^13 verringert, also auf ein 10-Billionstel!

Im Anschluss an den Laser und den Neutraldichtefilter kommt das Beugungsgitter mit 80 Linien/mm. Dieses konnte ich um ca. 30 Euro beim Schulmittelbedarf Ivo Haas erwerben. Dieses Beugungsgitter fächert nun den stark abgeschwächten Laserstrahl in mehrere Beugungsmaxima auf. In ca. 10 cm Abstand vom Beugungsgitter ist der Photomultiplier vom Typ Hamamatsu H5773 auf einen sog. Lineartisch festgemacht. Der Lineartisch (erhältlich auf ebay aus China für rund 50 Euro) sorgt dafür, dass man den Photomultiplier senkrecht zum Laserstrahl bewegen und somit die Maxima und Minima abfahren kann. Damit der Photomultiplier das Beugungsmuster auch wirklich gut räumlich auflösen kann, befindet sich vor seinem Eintrittsfenster ein schmaler Spalt. Würde ich sein gesamtes Eintrittsfenster verwenden, könnte ich die Intensität/Teilchenanzahl pro Sekunde in Abhängigkeit von der Position x nicht auflösen.

(Anmerkung: Diese Bilder zeigen das Beugungsmuster des Lasers natürlich noch OHNE Verwendung des Neutraldichtefilters!)

Der Vorteil des gewählten Photomultipliers Hamamatsu H5773 liegt darin, dass er in seinen sehr kleinen Abmessungen auch schon die zum Betrieb notwendige Hochspannung + Verstärker integriert hat. Er benötigt zum Betrieb lediglich +12V und liefert an seinem Ausgang bereits verstärkte Spannungspulse mit einer Amplitude von ca. 7V. Diese können dann sehr einfach weiterverarbeitet bzw. mit einem Zähler gezählt werden. Ich habe zum Glück auf ebay zwei Stück zu je 45 Euro erwerben können. Der Neupreis liegt bei rund 500 Euro/Stück!

Die Verstellmikroschraube des Lineartisches wurde von mir lichtdicht nach außen geführt, sodass man zur Veränderung der Position des Photomultipliers das Gehäuse nicht mehr öffnen muss. Der gesamte Verstellweg des Photomultipliers beträgt rund 8 mm. Dies reicht aber aus, um ca. 3 Beugungsmaxima zu erfassen.

Aufgetragen wird im abschließenden Graphen auf der y-Achse nicht wie bei Beugungsmustern gewohnt die Lichtintensität, sondern tatsächlich die Photonenzählrate in Photonen pro Minute! In den Maxima steigt diese auf bis zu 12000 Photonen pro Minute an.

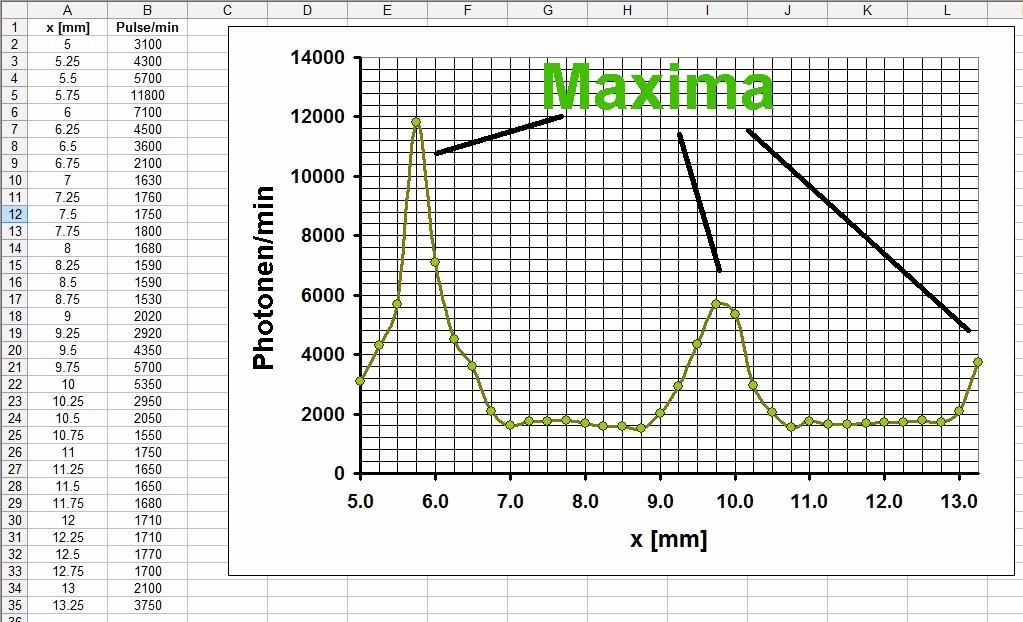
Mit diesem Experiment konnte ich also die Lichtteilchen einzeln/diskret registrieren und gleichzeitig damit ein Beugungsmuster aufzeichnen. Der Welle-Teilchen-Dualismus wurde also experimentell bestätigt.