Angenommen wir haben einen unterteilten Raum, wobei sich zu Beginn Teilchen der Sorte A nur links der Trennwand und Teilchen der Sorte B nur rechts von der Trennwand befinden. Öffnet man nun die Trennwand, so werden sich die beiden Sorten durch sog. Diffusion, also einer Art Transport vermischen. Nach einer bestimmten Zeit t werden die beiden Teilchendichten jeweils konstant sein, sprich die beiden Teilchensorten haben sich gleichmäßig im Raum verteilt.
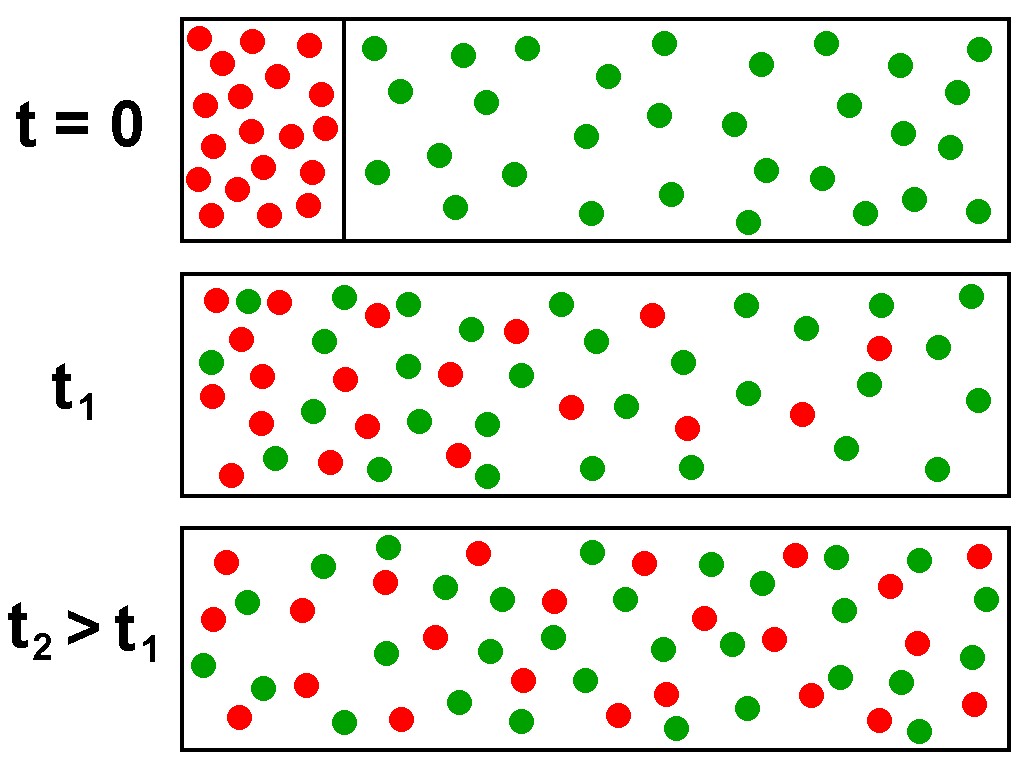
Diffusion ist demnach ein physikalischer Prozess, der zum Ausgleich von Konzentrationsunterschieden führt. Er wird durch die zufällige Eigenbewegung der Stoffteilchen (Brown’sche Molekularbewegung) verursacht.
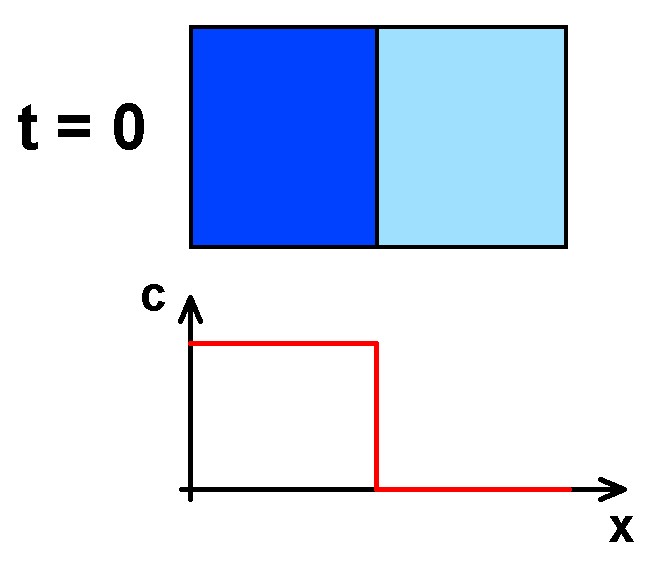
Betrachten wir zum Beispiel einen Behälter, in dem sich zum Zeitpunkt t = 0 rechts reines Wasser und links ein Farbstoff befindet. Die Konzentration c(x) des Farbstoffs gleicht also für t = 0 einer Stufenfunktion. Links ist c(x) ≠ 0 und rechts gilt c(x) = 0.
Durch die Brownsche Molekularbewegung wird sich aber der Farbstoff durch Diffusion schön langsam im gesamten Behälter verteilen. Die Konzentrationsfunktion c(x) wird sich also mit der Zeit ändern. Nach einer bestimmten Zeit wird die Funktion c(x) zum Beispiel wiefolgt aussehen:
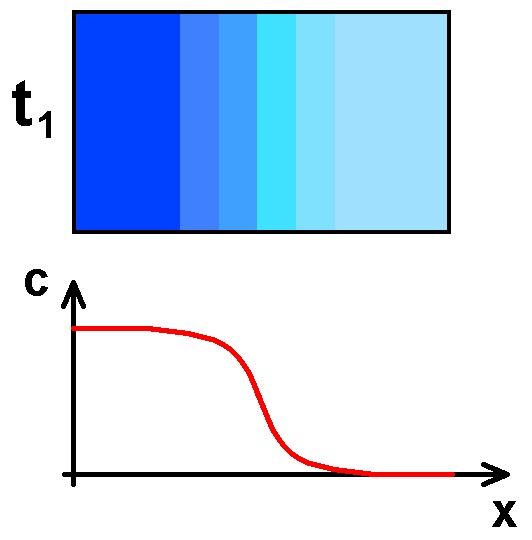
Warten wir noch länger, so wird sich der Farbstoff irgendwann einmal komplett gleichmäßig auf den gesamten Behälter verteilt haben. Die dazugehörige Konzentrationsfunktion c(x) sieht dann so aussehen:
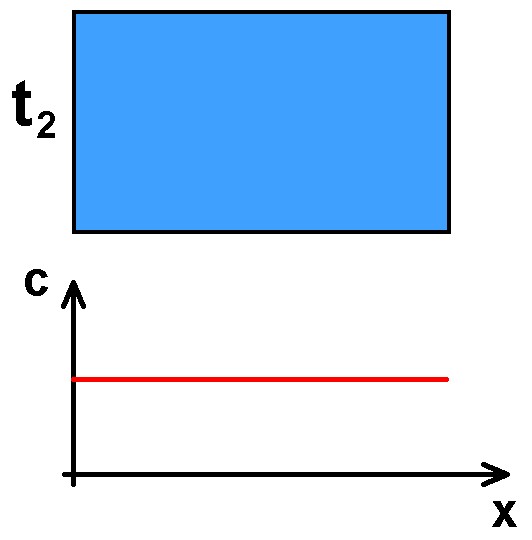
Die Konzentrationsfunktion c hängt also vom Ort x UND von der Zeit t ab, es gilt also c = c(x,t).
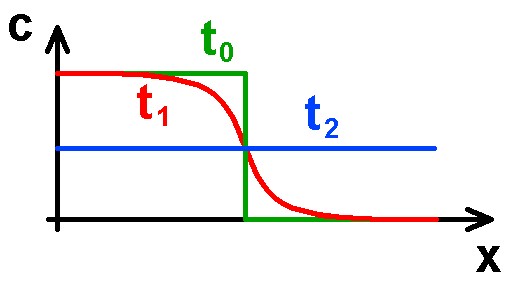
Kann man nun diese Funktion auch theoretisch berechnen, zum Beispiel für den oberen Fall?
Adolf Fick (1829 – 1901)
Bildquelle: Wikipedia
Ja, kann man. Grundlage dafür bilden die beiden Fick’schen Gesetze
Die Teilchenstromdichte J, also etwa der Teilchenstrom der Farbstoffmoleküle, hängt entscheidend von der örtlichen Änderung (= d/dx) der Konzentration c ab. Dazu zwei unterschiedliche Fälle zur Veranschaulichung:
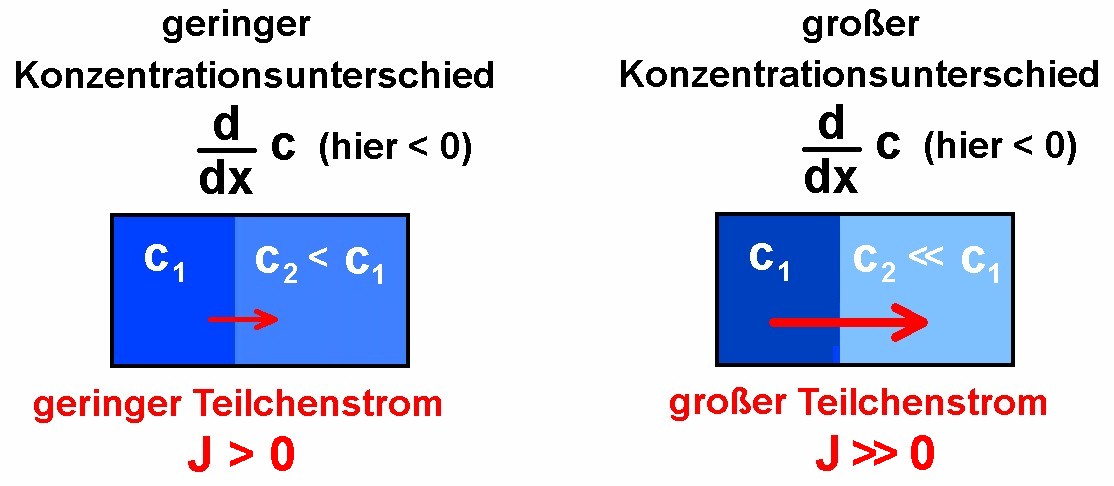
Der Teilchenstrom J beeinflusst aber wiederum über die Zeit t die örtliche Konzentration c. Hier kommt das zweite Fick’sche Gesetz zum Tragen, welches lautet:
Kann man dieses Gesetz auch veranschaulichen? Ja und zwar wiefolgt:
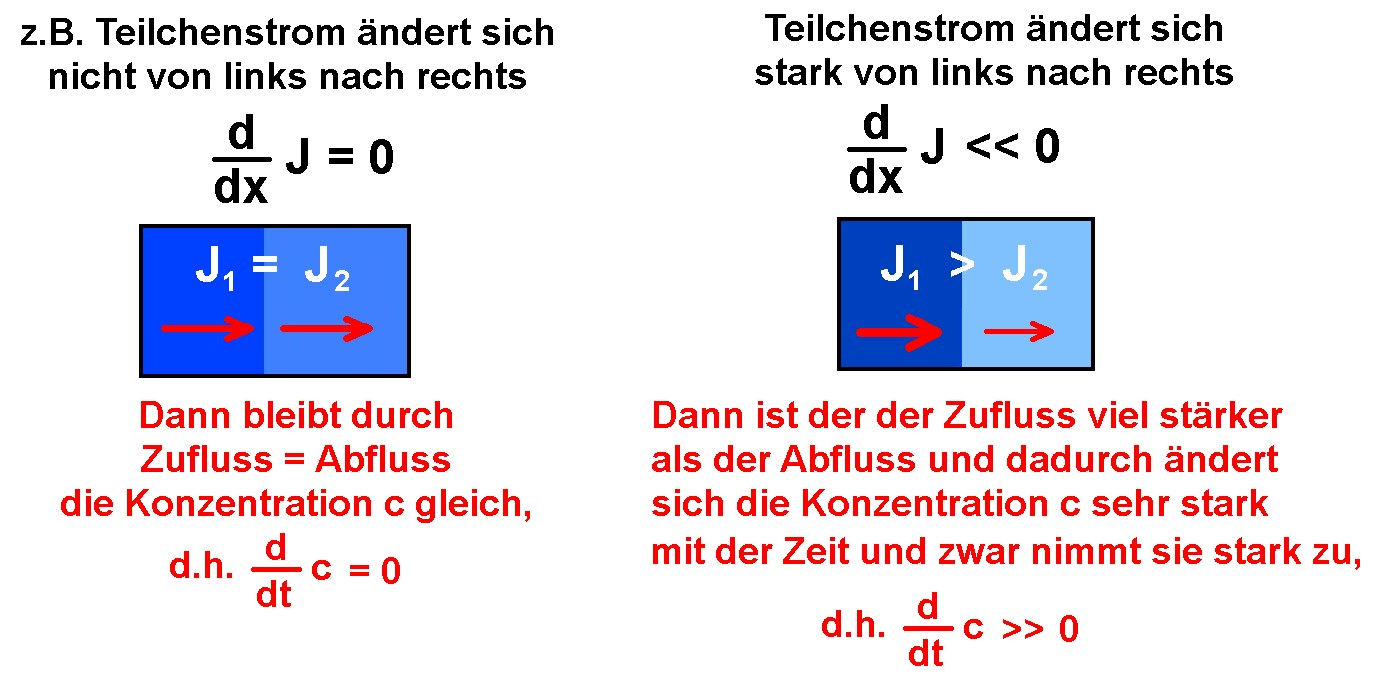
Die beiden Fick’schen Gesetze lassen sich nun kombinieren:
Konkretes Beispiel (nähere Informationen siehe https://lp.uni-goettingen.de/get/text/3665):
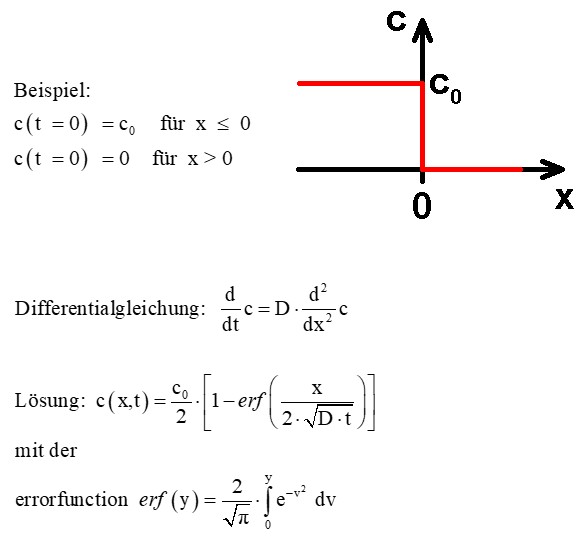
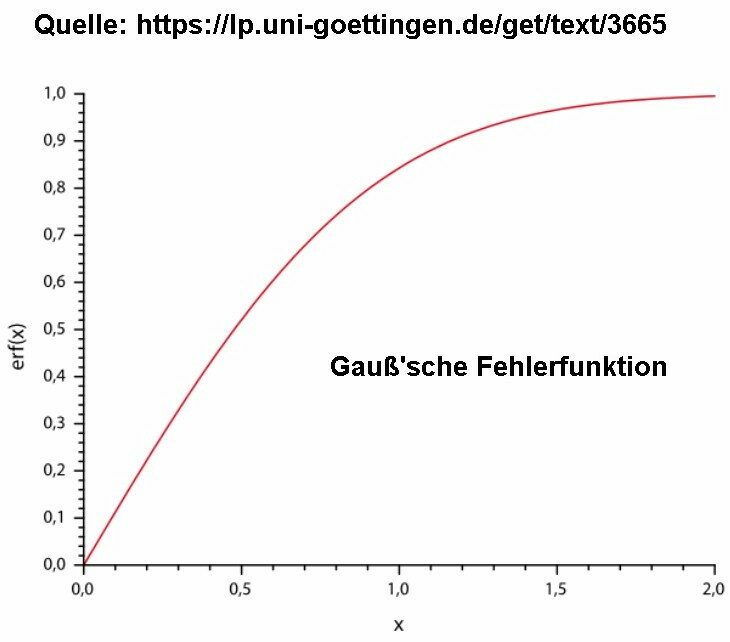
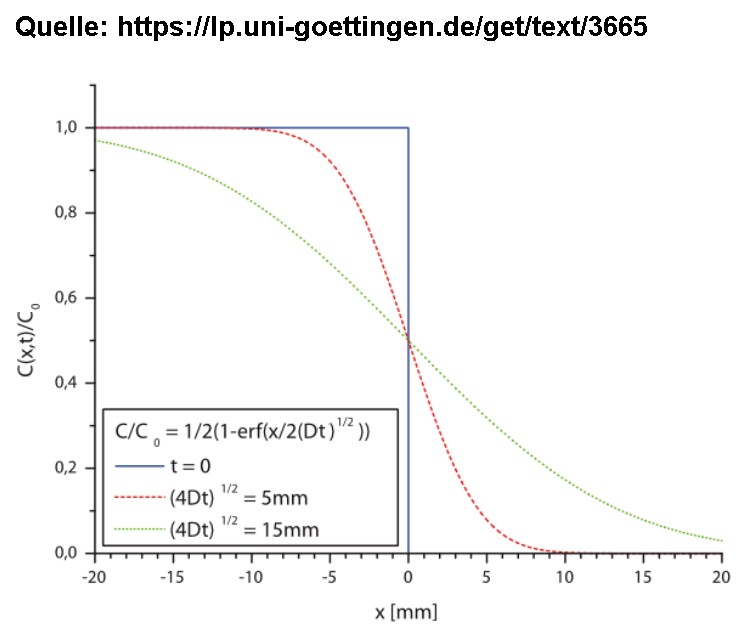
Theoretisches Ziel ist es also, bei gegebenen Startbedingungen die Ort- und Zeit-abhängige Konzentrationsfunktion c(x,t) zu finden. Wie bei all meinen Projekten steht ja das Experiment im Mittelpunkt, auch hier. Ich habe mir zur Überprüfung der Fick’schen Gesetze folgenden Aufbau ausgedacht:
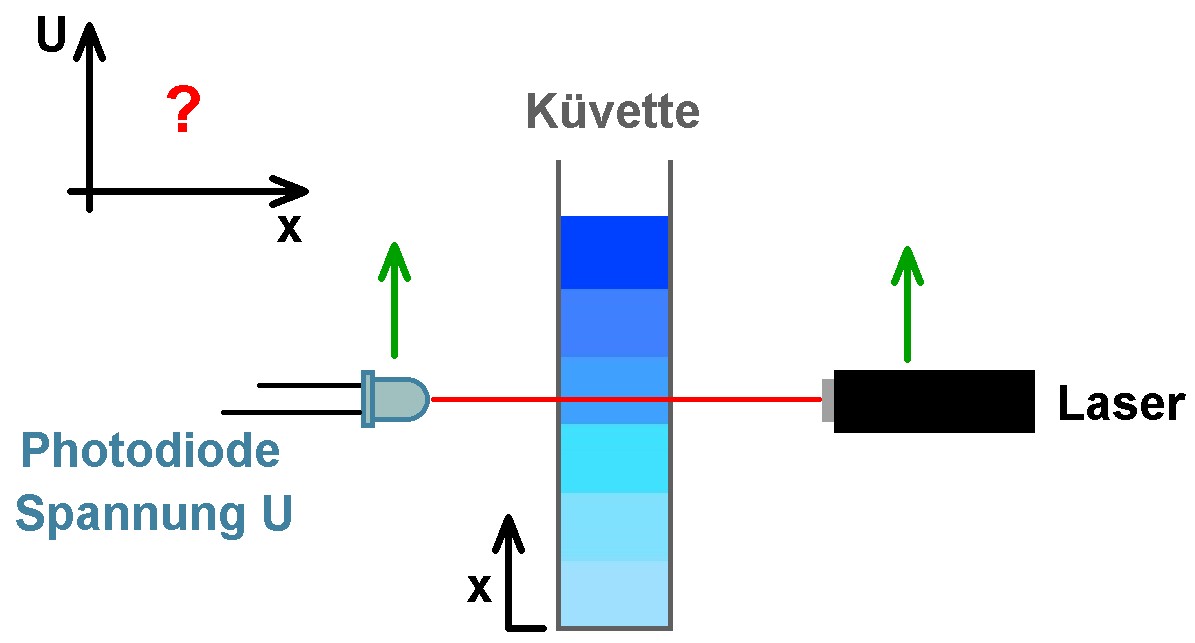
In die Küvette gebe ich zunächst reines Wasser. Danach fülle ich vorsichtig die Küvette mit einer Farbstofflösung (z.B. Methylenblau) auf. Nun fahre ich einen Laser von unten nach oben hoch und bestimme jeweils die an der Photodiode ankommende Spannung/Lichtintensität, also U(x). Dies wiederhole ich für verschiedene Zeiten und erhalte schlussendlich die Funktion U(x,t). Diese sollte ein Spiegelbild der Konzentrationsfunktion c(x,t) sein. Je stärker die Konzentration c, desto stärker die Abschwächung des Laserstrahls und desto geringer die Ausgangsspannung. U und c sind also gespiegelt.
Für die vertikale Positionsveränderung des Lasers und der Photodiode werde ich ein DVD-Laufwerk verwenden und dieses Schritt für Schritt mit einem Arduino ansteuern. Dies habe ich bereits bei einigen meiner Projekte so erfolgreich umgesetzt.
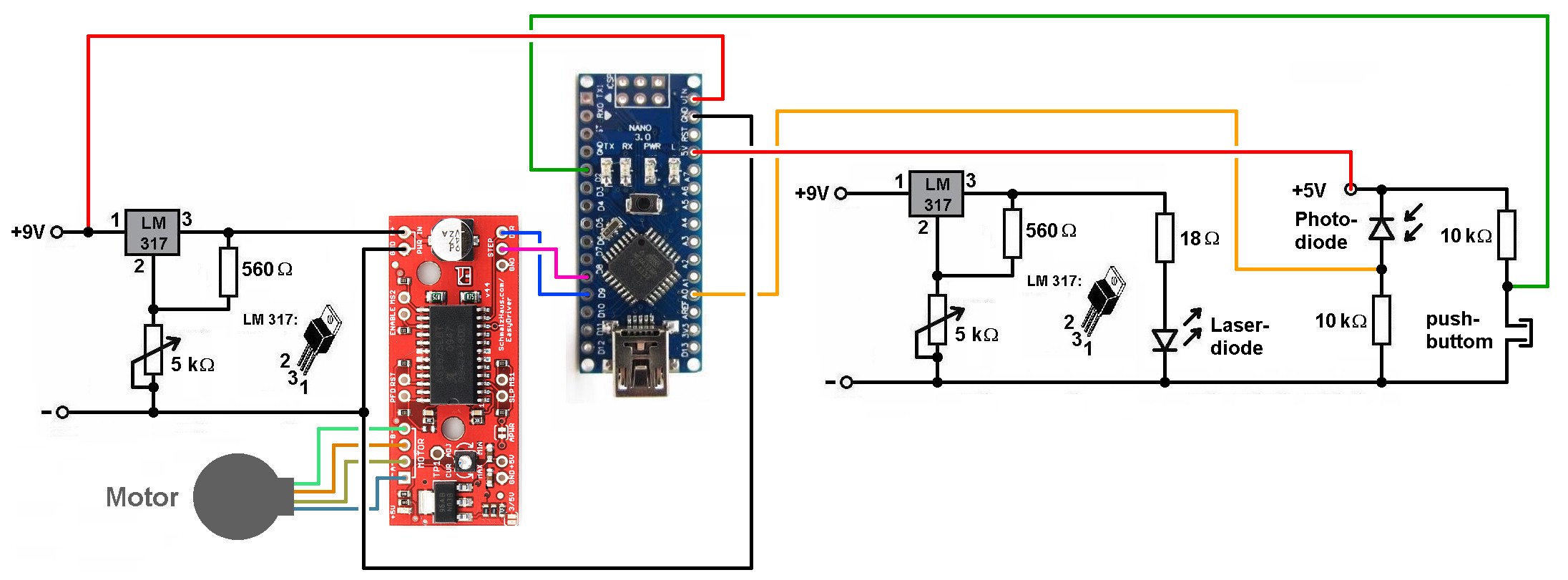
Der Schrittmotortreiber „EasyDriver“:
Für eigentlich fast alle meiner Arduino-Projekte verwende ich einen Nano:
Die kleine Platine mit der Spannungsregelung für die Laserdiode bzw. den Schrittmotortreiber, mit dem Taster zum Starten der Scans und mit der simplen Photodiodenschaltung bestehend aus der PD und einem Widerstand in Serie:
Die Photodiode SFH203:
Die auf dem DVD-Laufwerk verklebte Laserdiode und die M3-Gewindestange zur Aufnahme der Photodiode:
Als Farbstoff werde ich es zunächst mit meinen Lebensmittelfarben probieren. Ich habe aber auch Methylenblau auf ebay bestellt:
Der fertige Aufbau:
Als Testflüssigkeit habe ich es zunächst mit blauer Lebensmittelfarbe probiert. In das Wasser vorsichtig eingebracht löst sich diese aber sehr rasch auf. Also mit Ahornsirup vermengt und dann mit der Pipette unters Wasser geschichtet. Nach gut 12 Stunden hat sich aber leider die Lebensmittelfarbe noch immer nicht mit dem Wasser vermischt.
Also starte ich einen Versuch mit Kaliumpermanganat. Dieses hatte ich noch von meinem Photometer-Projekt bei mir zuhause:
Die Glasküvetten:
Unmittelbar nach dem Schichten der Kaliumpermanganatlösung sah es so aus:
Später dann so (letztes Photo nach ca. 14 Stunden):
Da die Diffusion also sehr lange dauert habe ich das Arduino-Programm abgeändert und lasse alles nicht mehr vollautomatisch machen sondern starte das Programm ca. alle Stunden manuell und führe einen einzelnen Scan durch.
Die Ergebnisse für die erste Mischung sahen dann wiefolgt aus:
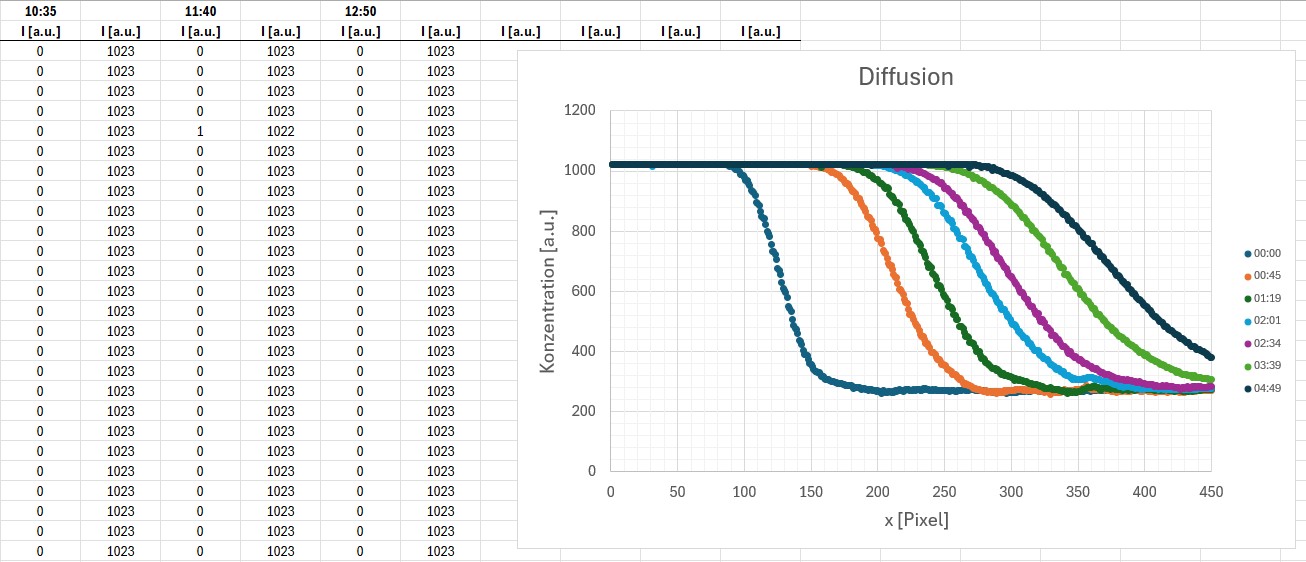
Wie man erkennen kann, war die Konzentration der Kaliumpermanganatschicht viel zu hoch. Denn selbst nach fast vollständiger Diffusion empfing die Photodiode kein Laserlicht (analoger Einlesewert = 0, umgerechnet auf Konzentration = 1023 – 0 = 1023):
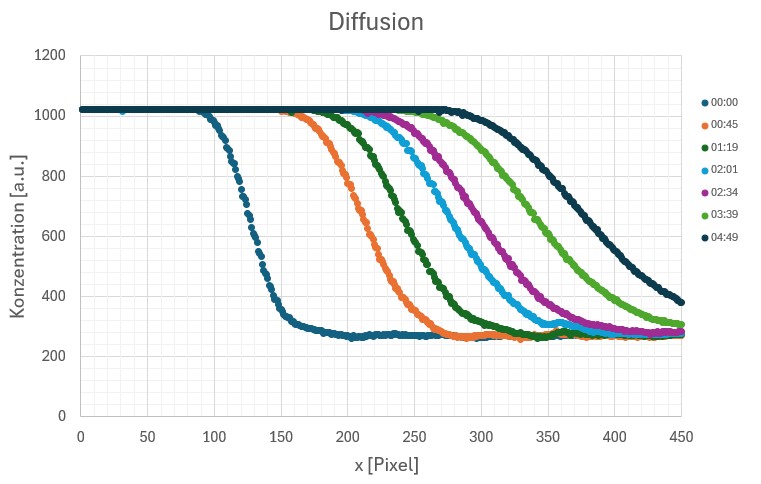
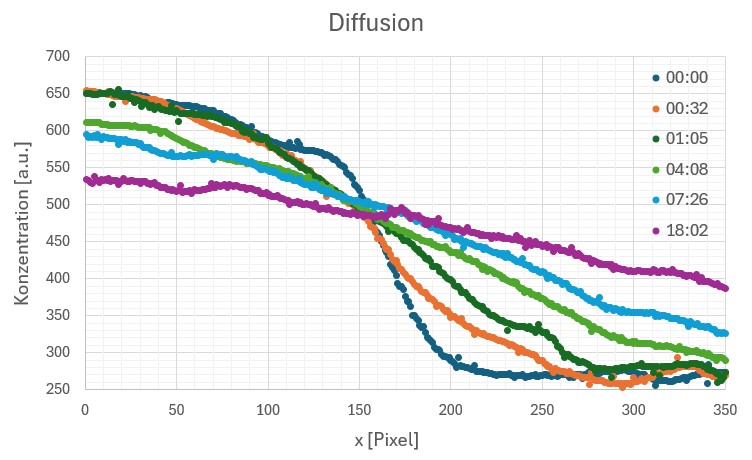
Daher musste ich die Konzentration der anfänglichen Kaliumpermanganatschicht erheblich reduzieren. Nun klappte es wie erhofft und meine „Kurven“ ähneln jenen laut Fickschen Gesetzen (siehe weiter oben) deutlich mehr, Heureka 😉
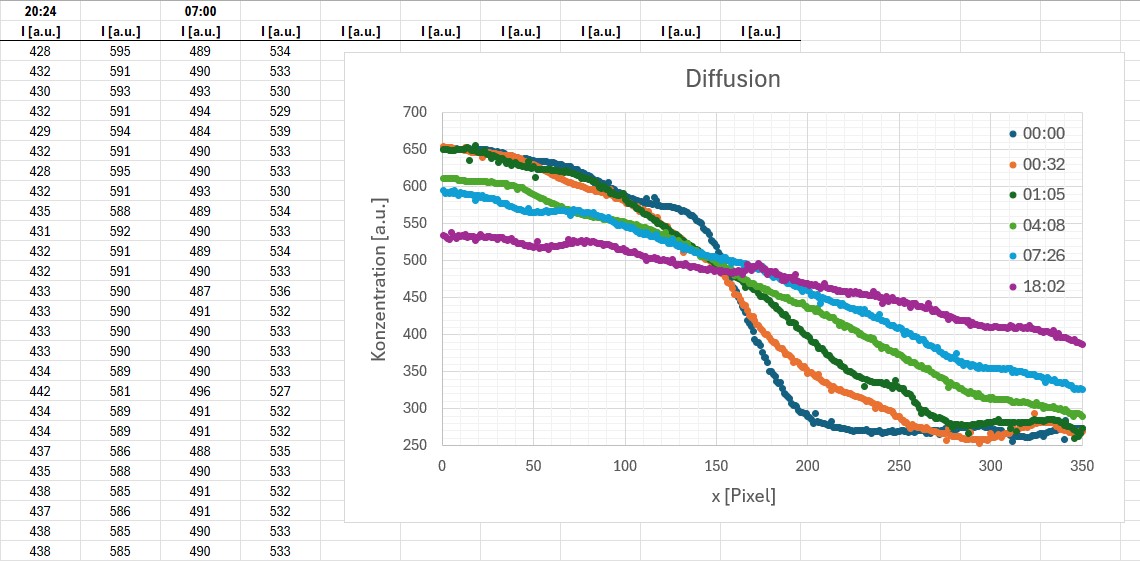
Hier noch das Youtube-Video:
Der simple Arduino-Code:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 |
#include <AH_EasyDriver.h> //AH_EasyDriver(int RES, int DIR, int STEP); // RES -> RESOLUTION per full revolve // DIR -> DIRECTION PIN // STEP -> STEPPING PIN AH_EasyDriver stepper(200,9,8); // Initialisation // DIR-Pin = Pin 9 // STEP-Pin = Pin 8 const int buttonPin = 2; // the number of the pushbutton pin int sensorPin = A0; // Analoger Input für die Spannung der Photodiode - analog input for the photodiode-voltage int U_photodiode; // Wert der Photodiodenspannung - voltagevalue of the photodiode void setup() { Serial.begin(57600); pinMode(buttonPin, INPUT); stepper.setSpeedRPM(20); // RPM , rotations per minute // RPM = 1 entspricht einer Umlaufszeit von 30 Sekunden!!! // RPM = 10 entspricht einer Umlaufszeit von 3 Sekunden!!! // RPM = 20 entspricht einer Umlaufszeit von 1.5 Sekunden!!! // ======================================================= //stepper.setMicrostepping(3); // 0 -> Full Step // 1 -> 1/2 microstepping // 2 -> 1/4 microstepping // 3 -> 1/8 microstepping //stepper.setSpeedHz(100); // Hz, steps per second stepper.move(1000,1); // Bewegt den Schrittmotor in die Startposition - move the stepper motor to the starting position } void loop() { while(digitalRead(buttonPin)); { // waiting start-button pressed; } Serial.println(" "); Serial.println("========================================================================"); Serial.println("komplett neue Messserie mit xxx Scans"); Serial.println(" "); for(int i = 1; i <= 2; i++) // Anzahl der Scans der Flüssigkeit = 2 { Serial.println(" "); Serial.print(i); Serial.println("-ter Scan:"); Serial.println(" "); for(int j = 1; j <= 500; j++) // Anzahl der Schritte eines einzelnen Scans { U_photodiode = analogRead(sensorPin); // Einlesen der Photodiodenspannung - reading of the photodiode-voltage // Serial.println(U_photodiode); Serial.println(1023 - U_photodiode); stepper.move(2,0); // Stepperschritte nach oben nach jeder Messung - steps upwards after each measurement delay(20); } stepper.move(500*2,1); // Laser wieder zurück zur Startposition - laser back to the starting position delay(10000); // Delay zwischen den einzelnen Scans - delay between the scans } } |
