Alphastrahlen gehören neben den Beta- und Gammastrahlen zur natürlichen Radioaktivität. Sie bestehen aus Heliumkernen, also aus 2 Protonen und 2 Neutronen. Ihr Durchdringungsvermögen ist sehr gering. Schon ein Blatt Papier reicht aus, um die Alphastrahlen vollständig zu blockieren. An Luft kommen sie auch nur wenige Zentimeter weit.
Es gilt näherungsweise für die Reichweite in Luft das Gesetz von Geiger:
Bei einer Energie von z.B. 5 MeV beträgt die Reichweite nur rund 35 mm. Wenn man einen Alphastrahler in einer Nebelkammer betrachtet so erkennt man, dass sämtliche Alphateilchen nahezu gleich weit kommen. Man erhält ein sog. Rasierpinselbild.
Bildquelle: https://www.lernhelfer.de/schuelerlexikon/physik/artikel/nebelkammer
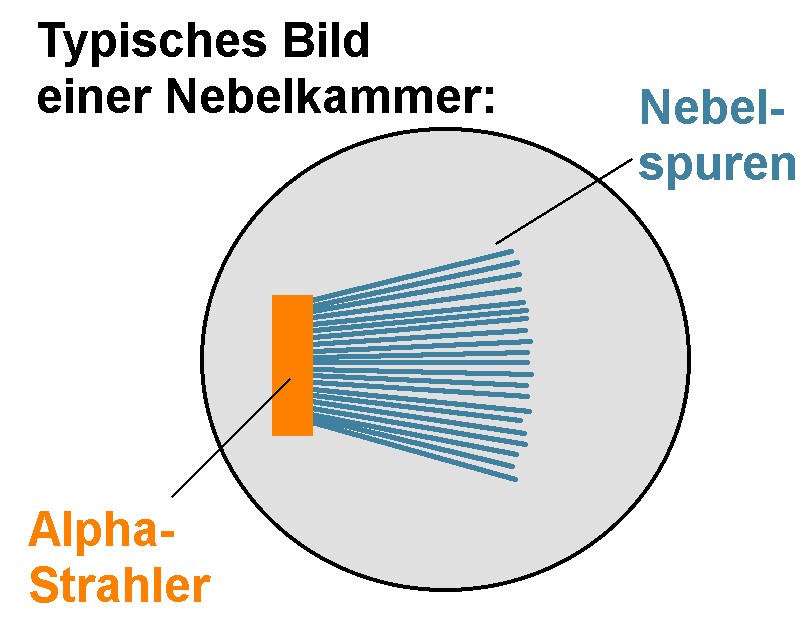
Warum ist dies so? Betrachten wir zunächst einmal Licht in einem absorbierenden Körper. Hier nimmt die Intensität nach dem Lambert-Beerschen Gesetz exponentiell ab. Die relative Abnahme innerhalb einer bestimmten Strecke (z.B. pro cm) ist unabhängig von der Intensität. So sinkt etwa die Intensität innerhalb eines Zentimeters vom Wert 100 auf 60, also um 40% bzw. vom Wert 5 auf 3, also auch um 40%.
Bei Alphastrahlen ist dies anders. Der Grund liegt darin, dass zur vollständigen Abbremsung von Alphateilchen sehr viele Stöße notwendig sind. Diese erfolgen zwar einzeln für sich betrachtet immer nach einer schwankenden Wegstrecke aber in ihrer Gesamtheit erfolgen sie innerhalb der Abbremsstrecke nahezu immer in gleicher Anzahl. Das kann man sich so vorstellen: Wenn man mit einem Würfel würfelt, so kommt die Augenzahl 6 immer nach einer unterschiedlichen Anzahl an Würfen. Man kann nicht vorhersagen, wann der nächste Sechser gewürfelt wird. Wenn man aber zum Beispiel 1 Million Würfe betrachtet, so kann man mit nahezu 100%iger Sicherheit sagen, dass die Anzahl der geworfenen Sechser sehr knapp um 1000000/6 = 166 666 liegen wird. Die Wahrscheinlichkeit, dass es zum Beispiel nur 100 000 Sechser sind oder weniger, ist nahezu 0. Dies nennt man auch das „Gesetz der großen Zahlen“. Umgemünzt auf die Alphateilchen kann man nicht genau sagen, welche Strecke sie zwischen 2 Stößen zurücklegen werden. Aber bei einer zur sog. freien Weglänge (= durchschnittliche Strecke ohne Kollisionen) sehr großen Gesamtstrecke zählt man nahezu immer eine äußerst ähnliche Anzahl an Gesamtstößen. Daher kommen Alphastrahlen mit einer bestimmten Energie immer nahezu gleich weit.
Für den Energieverlust pro cm, also dem Differentialquotienten dE/dx, gibt es die sog. Bethe-Bloch-Formel. Sie lautet:
Man kann erkennen, dass diese Energieabnahme pro Wegstrecke für kleinere Energien wächst. Dies bedeutet, dass die Energieabnahme pro cm zu Beginn, wenn die Alphastrahlen noch über eine hohe Energie verfügen, geringer ist und dann mit abnehmender Energie wächst. Die Kurve E(x), also die Energie in Abhängigkeit vom zurückgelegten Weg x, fällt also zu Beginn langsam ab und dann immer schneller. Diese Zusammenhänge lassen sich sehr gut mit EXCEL simulieren:
Die Simulation ergibt bei einer Teilchenenergie von 5500 keV eine Reichweite von ca. 3.6 cm. Dies deckt sich recht gut mit der obigen Näherungsformel von Geiger.
Excel-Programm: Radioaktivität_Alpha-Zerfall_Reichweite_Excel
Experiment:
Wie bei fast allen meiner Projekte gehört zur Theorie auch ein entsprechendes Experiment. Ich verfüge über zwei verschiedene Alphastrahler: Einmal Americium-241 und dann noch Polonium-210. Deren Alphaenergien betragen 5.486 (Am-241) bzw. 5.307 (Po-210). Laut Formel von Geiger müssten also die Alphateilchen in Luft 39.8 mm bzw. 37.9 mm weit kommen. Ich bin neugierig, ob ich diesen geringen Unterschied von nur 2 mm auch experimentell nachweisen kann.
Hinweis: Radioaktive Stoffe sind extrem gefährlich und bedürfen daher einer extremen Vorsicht und Achtsamkeit. Ich rate daher von Nachahmungen meines Versuchs ab!
Der Aufbau sieht wiefolgt aus:
Zur Vermeidung des 1/r²-Effekts (ganz unabhängig von der Reichweite nimmt ja die Intensität einer Strahlung mit 1/r² ab) verwende ich einen sog. Kollimator. Dieser lässt nur Teilchen mit einer bestimmten Richtung durch. Der Divergenzwinkel muss so gewählt werden, dass bei theoretisch unendlicher Reichweite immer alle Teilchen detektiert werden können und keine verloren gehen. In meinem Fall besteht der Kollimator aus 2 Kunststoffplatten im Abstand von ca. 6 mm, welche jeweils eine 2 mm Bohrung besitzen.
Als Geigerzähler kommt mein Endfensterzählrohr ZP1401 zum Einsatz. Dieses ist auch für Alphastrahlen geeignet.
So, der Aufbau ist soweit fertig. Es können nun beide Alphastrahler einfach positioniert werden:
Die ersten Messungen sind absolviert, aber die Ergebnisse sind ernüchternd. Bei Verwendung des Kollimators sind die Zählraten trotz Vergrößerung der beiden Löcher im Kollimator auf 3.5 mm extrem niedrig und nur geringfügig höher als der Hintergrund.
Das Problem ist auch, dass durch die Dicke des Kollimators die Messungen erst ab einer Distanz von 3 cm starten können. Die erhoffte Stufenfunktion ist leider in keinster Weise zu messen.
Daher habe ich den Kollimator entfernt und die Messungen mit folgenden Hintergedanken wiederholt: Nehmen wir an, die Zählrate N(x) in Abhängigkeit von der Distanz x besitze die Form einer Potenzfunktion. Es gilt also
Die Hoffnung war nun, dass ich bis zur Reichweite der Alphateilchen eine Gerade mit k = -2 bekomme, da bis dahin das 1/r²-Gesetz gelten sollte. Ab der Reichweite der Alphastrahlen sollte die Gerade einen Knick/eine Stufe besitzen, da ja ab dieser Distanz keine Alphateilchen mehr den Detektor erreichen. N = 0 würde demnach lg(N) = – ∞ bedeuten. Stattdessen erhalte ich folgende Messwerte bzw. folgenden Verlauf:
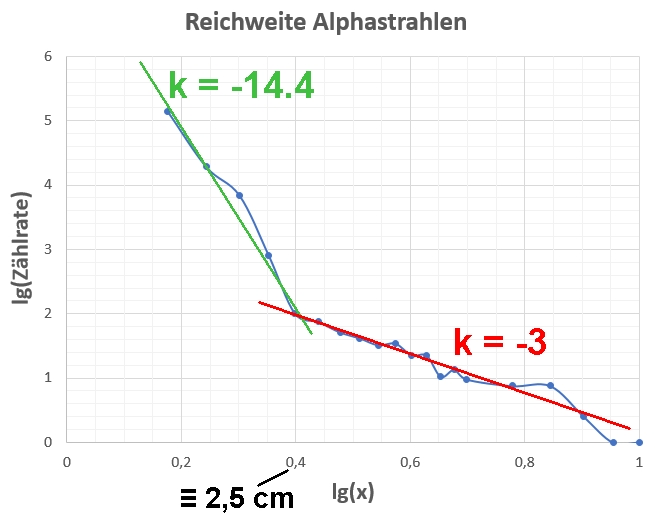
Zu Beginn für Abstände x < 2.5 cm, was einem lg(x) = 0,4 entspricht, besitzt die erhaltene Gerade einen Anstieg von -14.4. Dies würde bedeuten, dass in diesem Bereich die Zählrate N(x) mit 1/x^14.4 abnimmt. Bei x = 2.5 cm, sprich lg(x) = 0,4 besitzt dann die Gerade einen Knick. Für Distanzen x > 2.5 cm, also lg(x) > 0.4, erhalte ich eine weitere Gerade mit dem Anstieg k = -3. Dies würde dann einer Potenzfunktion N(x) = 1/x^3 entsprechen.
Ehrlich gesagt bin ich ein wenig ratlos, was diese Messergebnisse betrifft. Ein Problem ist mit Sicherheit, dass das verwendete Polonium-210 auch ein schwacher Gammastrahler ist. In 0.001% aller Zerfälle wird ein Gammaquant mit 0.803 MeV emittiert. Bei einer angenommenen Aktivität von ca. 6.5 Millionen Zerfällen pro Sekunde zum Zeitpunkt des Experiments, sind dies immerhin 65 Gammaquanten pro Sekunde. Und diese besitzen in Luft im Gegensatz zu den Alphateilchen keine wirklich eingeschränkte Reichweite.
Zudem muss wohl auch noch berücksichtigt werden, dass die Strahlungsquelle konkret kein Punktstrahler ist. Es stellt sich auch die Frage, welche Energie die Alphateilchen noch mindestens besitzen müssen, damit sie in das Endfensterzählrohr eindringen können und einen Puls auslösen. Eventuell haben sie genau im Abstand x = 2.5 cm, was einem lg(x) = 0.4 entspricht, nicht mehr diese notwendige Energie. Warum dann aber bei lg(x) = 0.4 kein Sprung erfolgt, ist mir ein Rätsel.
Eigentlich hätte ich nämlich so etwas erwartet:
Habe heute noch Messungen mit dem Americium-241 gemacht. Als Kollimator verwendete ich eine Distanzhülse mit 15 mm Länge. Aber auch hier erhalte ich wenig zufriedenstellende Ergebnisse. Die Zählrate in Abhängigkeit vom Abstand zeigt leider keinen (deutlichen) Sprung bei ca. 4-5 cm Abstand durch den Wegfall der Alphastrahlen. Erschwerend kommt auch noch die Gammaaktivität von Am-241 hinzu.
Hier die experimentellen Ergebnisse mit Americium-241 und Kollimator:
Bei einem Abstand von ca. 4.5 cm ist mit viel Vorstellungskraft ein leichter Sprung zu erkennen:
Trage ich die Zählraten und Abstände logarithmisch auf, so erhalte ich eine Gerade mit dem Anstieg k = ca. –2. Mein Endfensterzählrohr hat scheinbar eine zu geringe Eintrittsöffnung, um wirklich immer alle Alphateilchen unabhängig vom Abstand erfassen zu können. Also bekomme ich selbst mit Kollimator bei den Alphastrahlen eine 1/r²-Abhängigkeit hinein. Wenn ich aber die Strahlen mittels kleinerer Öffnungen besser kollimiere, erhalte ich wiederum zu geringe Zählraten. Also alles gar nicht so einfach. An eine Unterscheidung der Alphaenergien von Am-241 und Po-210 ist gleich gar nicht zu denken. Deshalb bin ich gerade dabei, ein einfache Alphaspektroskopie mittels Photodiode BPX61 umzusetzen.
Ich habe dieses Experiment hier bewusst dokumentiert um zu zeigen, dass Experimente bei weitem nicht immer so verlaufen, wie man es erwartet bzw. gerne hätte. Dies ist in der Experimentalphysik hingegen Alltag, auch wenn vielleicht so mancher Physiker nur ungern darüber spricht 😉
