Belastet man eine Feder mit einer Kraft F, so wird sie um eine Länge Δx gedehnt. Zwischen F und Δx herrscht eine direkte Proportionalität, das sog. Hook’sche Gesetz: F = k · Δx.
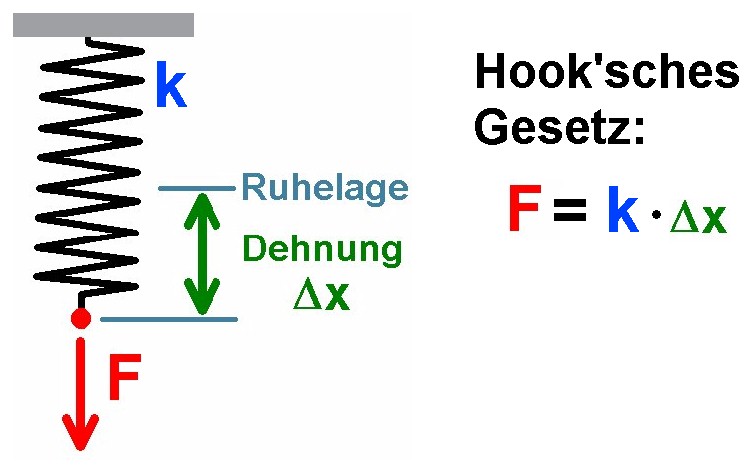
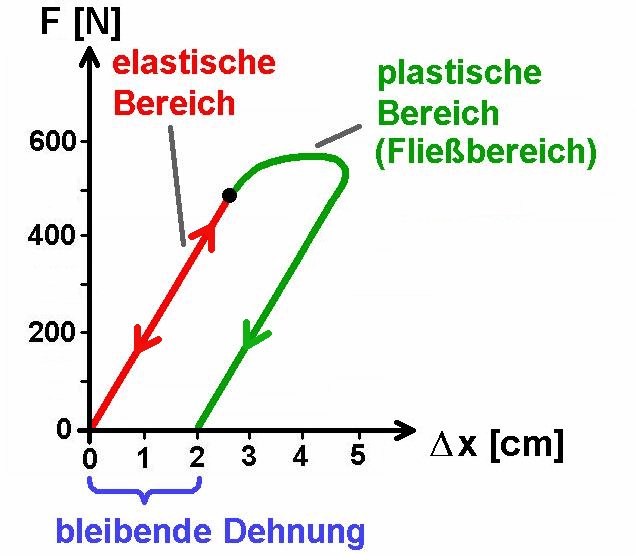
Der Proportionalitätsfaktor k wird Federkonstante genannt. k entspricht genau der Kraft F zur Dehnung der Feder um Δx = 1 m. Eine harte Feder hat demnach eine große Federkonstante und eine weiche ein kleines k. Das Hook’sche Gesetz gilt natürlich nicht für beliebig große Dehnungen. Irgendwann verlässt die Feder ihren elastischen Bereich und verformt sich plastisch/dauerhaft.
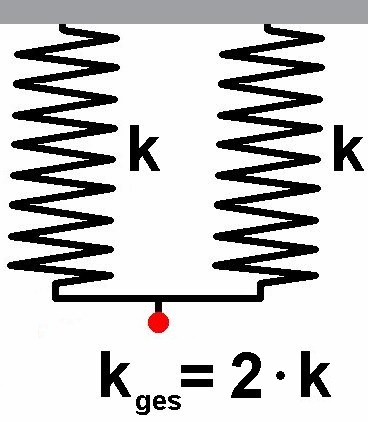
Postiert man zwei gleiche Federn parallel zueinander, so besitzt die „Gesamtfeder“ die doppelte Federkonstante. Zwei gleiche Federn hintereinander/in Serie ergibt nur die halbe Federkonstante:

Vielleicht kennt ja der eine oder andere solche zumeist bunten Spiralfedern zum Spielen. Das englische Original heißt „Slinky“:

Genau um eine solche Feder soll es in diesem Experiment gehen. Hält man die Feder an einem Ende fest und lässt sie nach unten hängen, so kann man folgendes Beobachten: Die Abstände zwischen den einzelnen Windungen nehmen nach oben hin zu. Dies ist auch logisch, denn an einer einzelnen Windung weiter oben hängt bereits eine größere Masse als weiter unten.
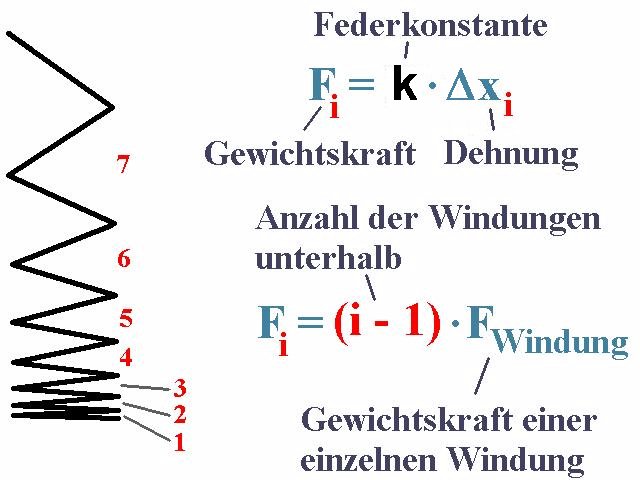
An der untersten Windung hängt keine weitere Windung. Von daher müsste ihre Dehnung gleich Δx1 = 0 sein. An der zweiten Windung hängt nun aber bereits eine Windung mit der Masse mWindung bzw. der Kraft mWindung · g. Die zweite Windung wird also um Δx2 = F/k = mWindung · g / kWindung gedehnt. kWindung ist dabei die Federkonstante einer einzelnen Windung. Für die dritte Windung müsste gelten: Δx3 = F/k = 2 · mWindung · g / kWindung usw. Für die Masse einer einzelnen Windung gilt: mWindung = mFeder / Anzahl der gesamten Windungen n. Wir haben es hier also mit einer arithmetischen Folge zu tun. Mit jeder weiteren Windung kommt die Dehnung mWindung · g / kWindung hinzu.


Die Gesamtmasse meiner Feder (insgesamt n = 36 Windungen) beträgt mFeder = 47.3 g:

Hier sieht man schön die nach oben hin zunehmenden Dehnungen:





Die einzelnen Dehnungen habe ich mit der Software „Tracker“ ausgewertet:
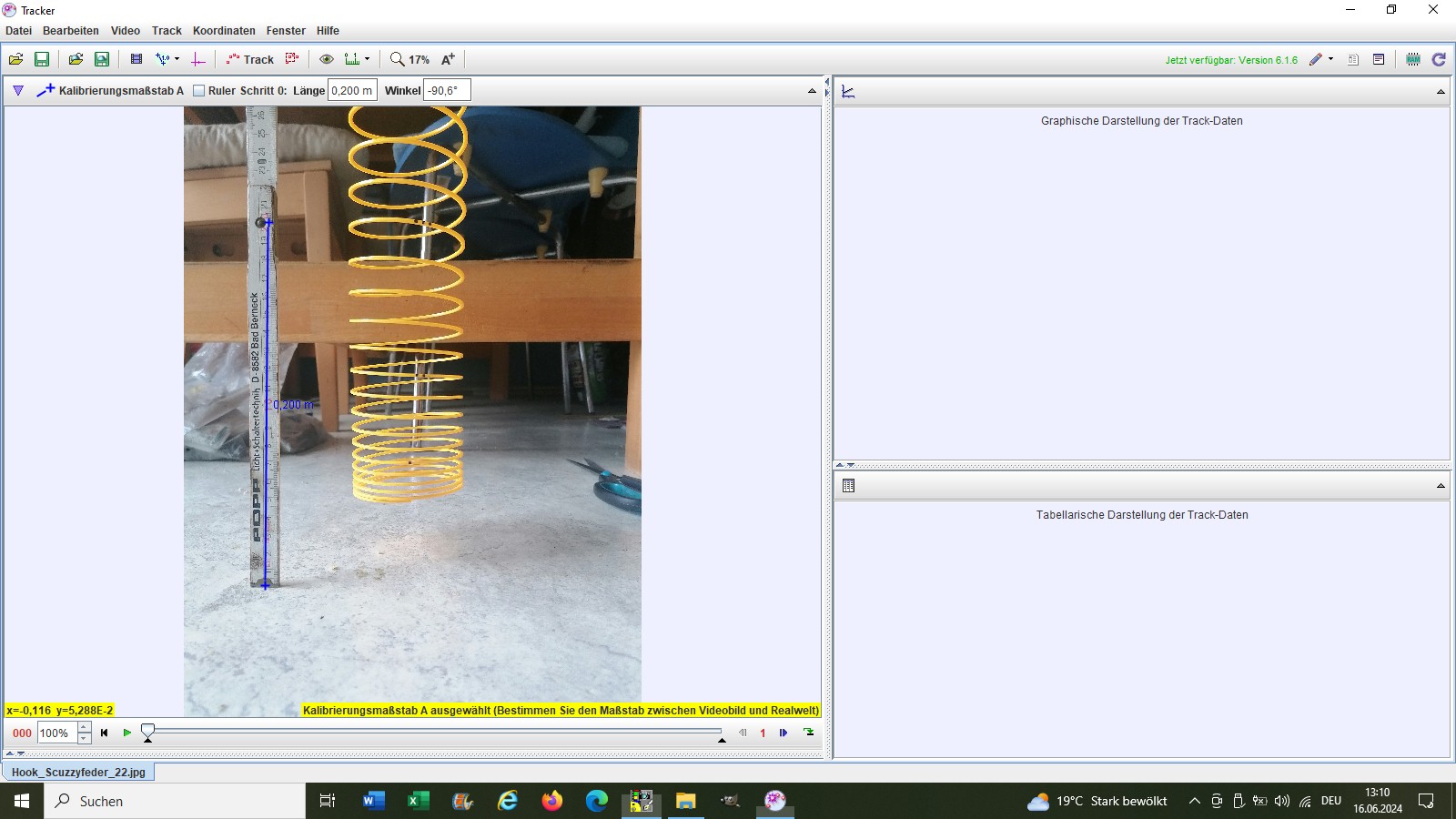
Hier der Verlauf x(i) [Ort der i-ten Dehnung] bzw. Δx(i) [i-te Dehnung]:

Die einzelnen Dehnungen nehmen wie erwartet einigermaßen linear zu:
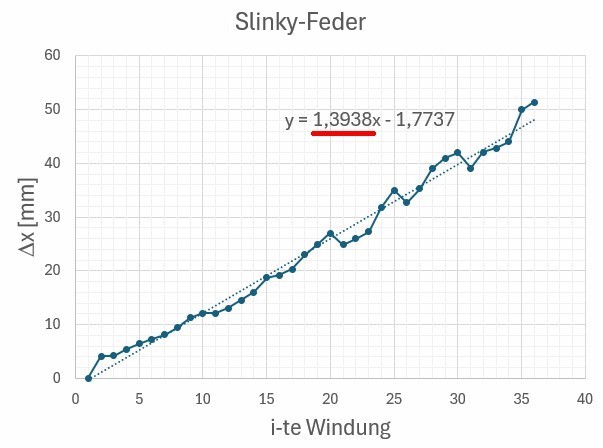
Pro weiterer Windung nehmen die Dehnungen um 1.3938 mm (= Geradenanstieg) zu. Dieser Wert entspricht wie oben beschrieben genau dem Ausdruck mWindung · g / kWindung. Für die Federkonstante einer einzelnen Windung folgt dann: kWindung = mWindung · g / 0.0013938.

Um auf die Gesamtdehnung der 36 Windungen zu kommen, muss die arithmetische Folge aufsummiert werden. Sie wächst ca. mit (n – 1) · n ≈ n². Ich komme konkret auf eine Gesamtdehnung von 87.8 cm, was ich experimentell recht gut bestätigen konnte:


Wir kennen nun die Federkonstante einer einzelnen Windung und zwar kWindung = 9.246 N/m. Die gesamte Feder besteht aber aus 36 „Einzelfedern“ hintereinander. Für die Federkonstante der gesamten Slinky-Feder müsste demnach gelten: kges = kWindung / 36 = 0.257 N/m. Dies habe ich noch experimentell überprüft, indem ich an die Feder eine Masse m = 25.26 g gehängt und die Dehnung bestimmt habe.

Abstand der unbelasteten Feder zum Boden = 111 cm:

Als Gewicht verwendete ich eine große Mutter:



Der Abstand der belasteten Feder zum Boden betrug 24 cm:

Hier noch die Rechnung:
 Die experimentell ermittelte Federkonstante kges der gesamten Feder weicht mit 0.285 N/m etwas vom theoretisch hergeleiteten Wert 0.257 N/m ab…
Die experimentell ermittelte Federkonstante kges der gesamten Feder weicht mit 0.285 N/m etwas vom theoretisch hergeleiteten Wert 0.257 N/m ab…
In meiner Jugend waren die aufkommenden Mountainbikes noch durchgängig starr ohne Federung, sog. hardtails. Erst seit ca. mitte der 90er Jahre kamen dann immer mehr an der Front (Federgabel) und auch am Hinterrad gefederte (Fullsuspension) Modelle auf den Markt.
Ich bei einem Rennen im Jahr 1995:

Hier mein von KTM gesponsertes high-tech Wettkampf-Fully, mit dem ich 1996 an den Start hätte gehen sollen:

Um die Kennlinien der Federelemente soll es in diesem Experiment gehen.
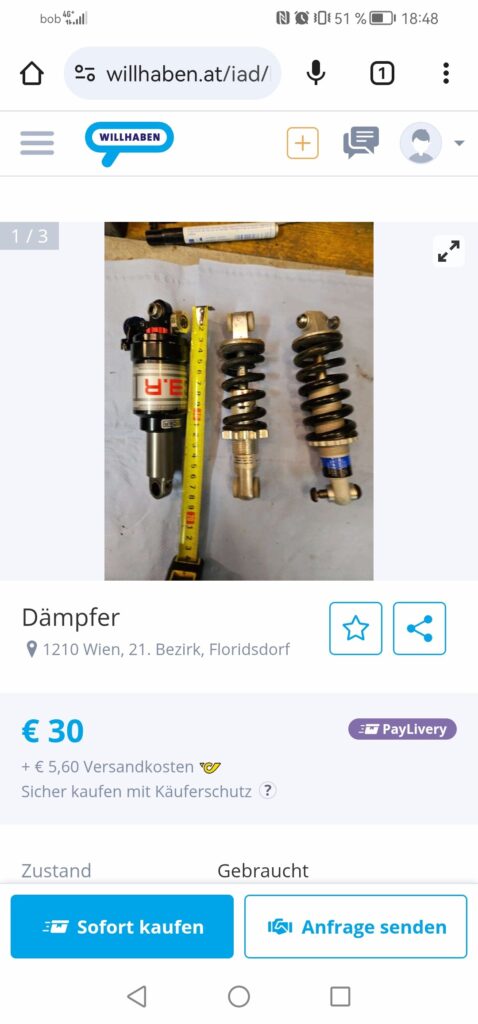
Dazu habe ich mir auf der österreichischen Verkaufsplattform http://www.willhaben.at gebrauchte Federelemente besorgt und zwar zwei Modelle mit Feder und einen luftgefederten Dämpfer.

Der Luftdämpfer MC3.R von Rock Shox:

Die beiden Modelle mit klassischer Feder:


Auf der einen Feder kann man die angegebene Federkonstante k = 750 LBS/inch = 1313 N/cm erkennen. Das entspricht immerhin dem Gewicht von 134 kg für 1 cm Federweg!

Hier der schematische Messaufbau:
Die 10 mm starken Ankerplatten aus Stahl habe ich mir ebenfalls über willhaben besorgt:


Einen günstigen Wagenheber für bis zu 2 t Hublast fand ich bei http://www.pollin.de:


Ich meide ja Kaufhäuser wie der Teufel das Weihwasser aber in Baumärkten treibe ich mich eigentlich doch recht gerne herum. Kein Wunder, finde ich da auch meistens Sachen für meine experimentellen Projekte. In diesem Fall waren es M12 Gewindestangen und M12 Muttern und Beilagscheiben…






Für den Luftdämpfer benötigte ich noch eine Dämpferpumpe bis 300 psi (= ca. 21 bar):



Unter der Kennlinie versteht man konkret die notwendige Kraft in Abhängigkeit vom Federweg, also F(x). Bei einer Federdämpfung erwartet man einen weitgehend linearen Verlauf. Bei Luft als Dämpfer ist dies jedoch anders. Nach dem Gesetz von Boyle-Mariotte gilt ja für den isothermen Fall (Temperatur T = konstant): p · V = konstant. Halbiert man also das Luftvolumen V, so steigt der Druck p auf das Doppelte an. Der Graph ist demnach progressiv und steigt zunehmend an:
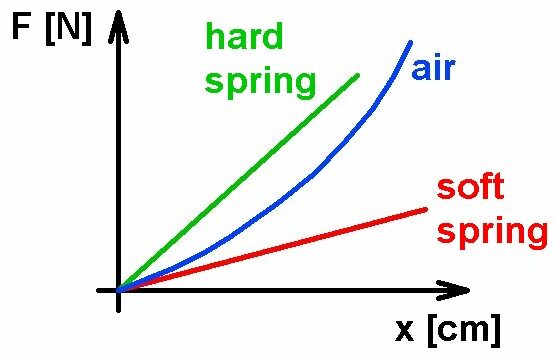
Ein Luftdämpfer hat demnach den Vorteil zu Beginn noch weich und sensibel zu sein aber dann zunehmend härter zu werden um dennoch einen guten Durchschlagschutz zu bieten. Bei einer Feder bräuchte man für letzteres eine harte und demnach zu Beginn unsensible Feder.
Für die Kennlinie benötigt man auch einen Kraftsensor. Auf aliexpress bin ich fündig geworden:



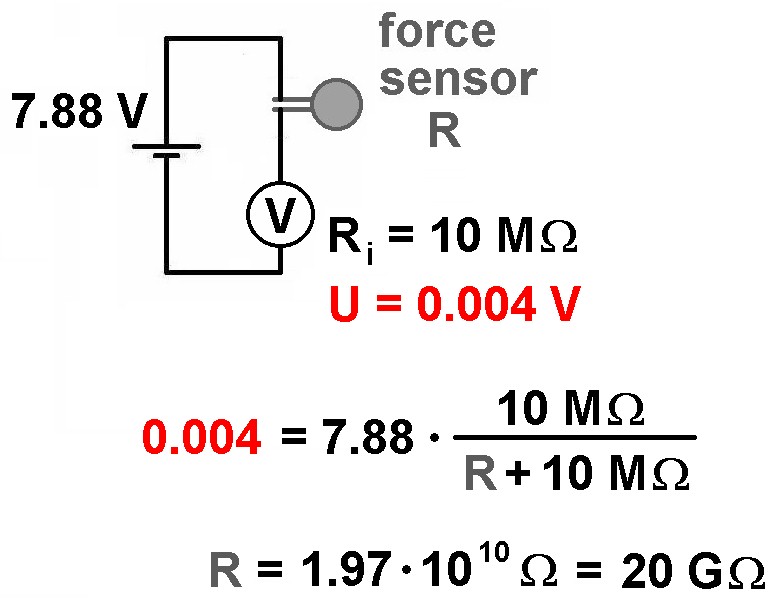
Bevor ich die Wheatstonebrücke für den Sensor konzipiere, habe ich mir einmal dessen Widerstände u.a. ohne Belastung angesehen. Bei F = 0 N konnte ich aber mit meinem Multimeter den zu hohen Widerstand nicht mehr erfassen. Also verschaltete ich den Sensor in Serie mit dem Voltmeter und schloss es an eine Batterie mit U = 7.88 V an. Mit dem bekannten Innenwiderstand des Voltmeters von 10 MΩ und der angezeigten Spannung von nur 0.004 V lässt sich der Widerstand des Kraftsensors zu beachtlichen 20 Gigaohm bestimmen.


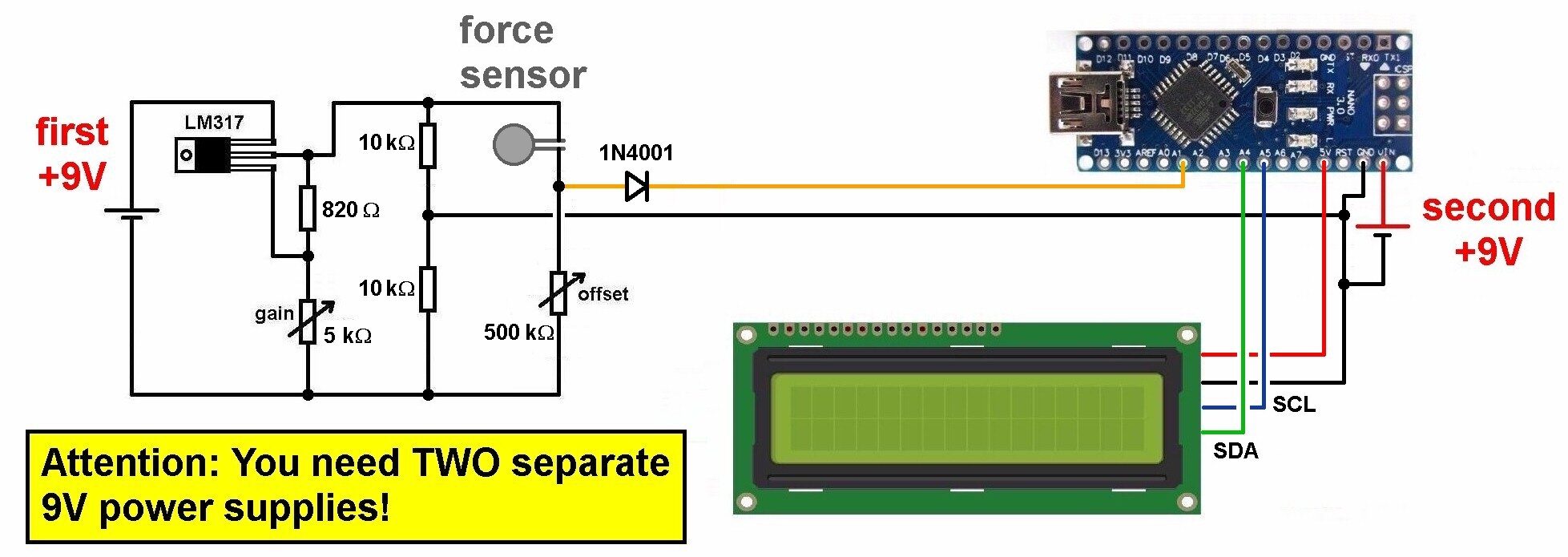
Drückt man mit dem Finger aber kräftig auf den Sensor, so sinkt dessen Widerstand sehr stark ab und kommt in einen Bereich um die 100 kΩ. Daher wählte ich für das Potentiometer/Spindeltrimmer in der Wheatstonebrücke einen Wert von 500 kΩ:




Ohne Kraft:

Mit Kraft:

Die Kennlinie meines Kraftmessers dürfte allerdings problematisch sein, denn die Ausgangsspannung scheint bei sehr hohen Kräften kaum mehr anzusteigen. Und dann ist da auch noch das Problem mit der Kalibrierung. Ich habe mich deshalb auf Amazon nach einer extrem kompakten Personenwaage umgeschaut und folgendes Modell gekauft:
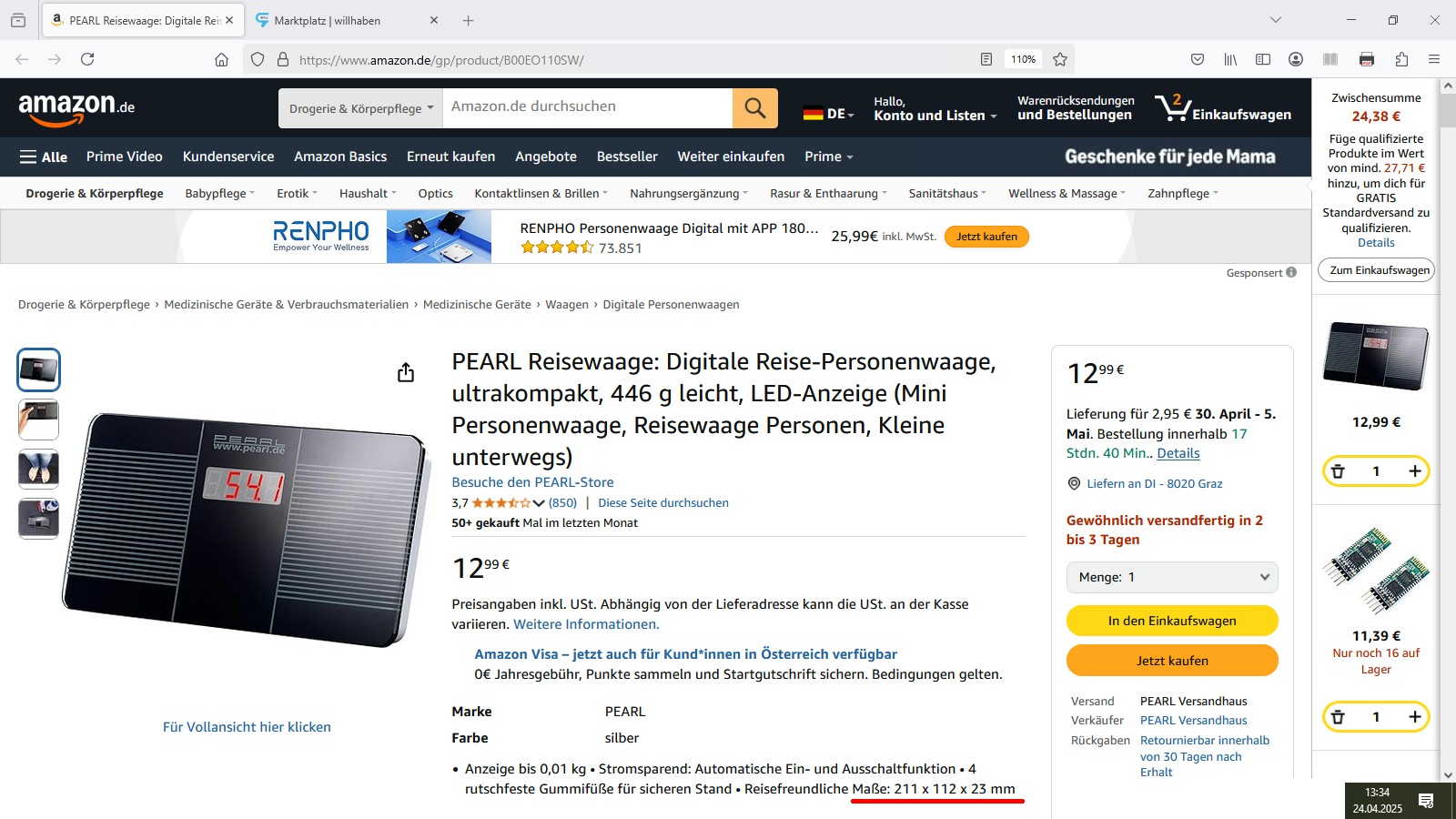
Wenn sich mein resistiver Kraftsensor also für große Kräfte als nicht geeignet erweist, kann ich dann noch immer die kompakte Personenwaage nicht bloß zum Kalibrieren, sondern als dauerhaften Kraftmesser benutzen, mal schauen…
Zum Schutz des Sensors habe ich mir aus einer 40 mm breiten Aluleiste eine Ronde ausgesägt:



So, heute habe ich einmal einen ersten rein qualitativen Testlauf mit dem Kraftsensor unternommen. Wie ich befürchtet habe, ist der resistive Sensor eigentlich nicht wirklich zu gebrauchen, da die Ausgangsspannung mit zunehmender Kraft extrem abflacht. Sie steigt bei bereits geringster Kraft auf über 3 V an um dann letztendlich nicht merklich über 4 V zu gehen. So kann ich den Sensor nicht wirklich gebrauchen. Ich werde also komplett auf ihn verzichten und mir stattdessen die Kraft mit der kompakten Personenwaage anzeigen lassen.



In dieser Bilderserie erkennt man deutlich die Problematik:

In der Zwischenzeit ist die kompakte Personenwaage von Pearl angekommen:





Die „professionelle“ Anzeige des Federwegs:

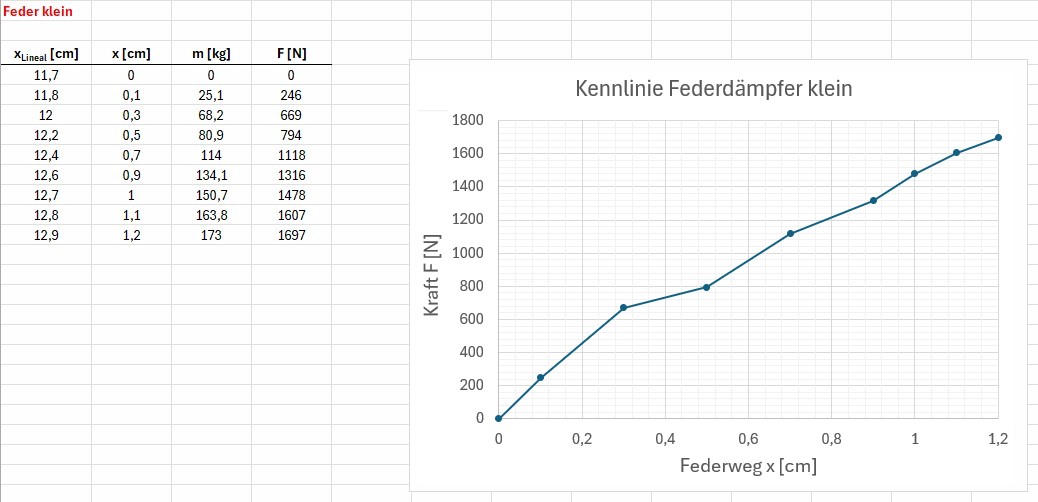
Die beiden Federdämpfer zeigen eine annähernd lineare Kennlinie, wie man sie vom Hook’schen Gesetz her erwarten würde:

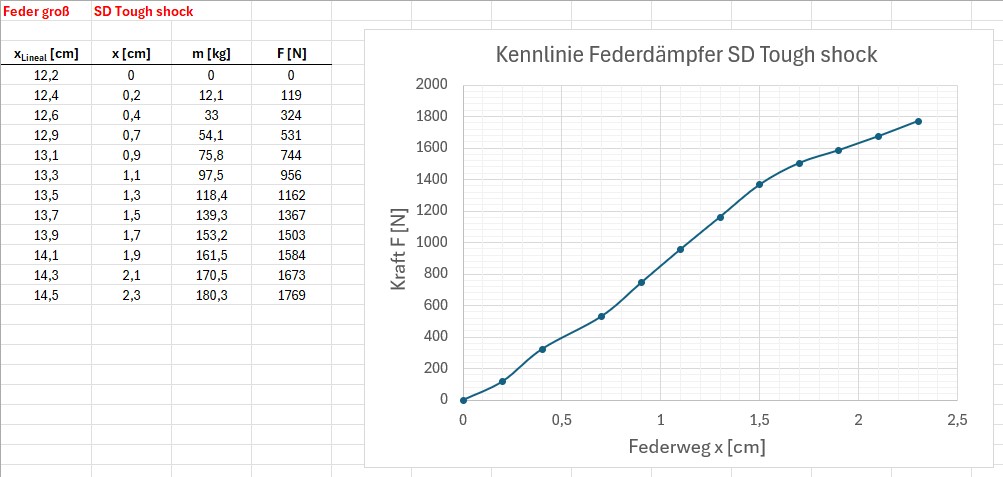
Die Feder des kleineren Dämpfers ist mit 750 lbs/inch angegeben, was einer Federkonstanten von 1313 N/cm entspricht. Der Anstieg meiner Kennlinie liegt in etwa in diesem Bereich 😉
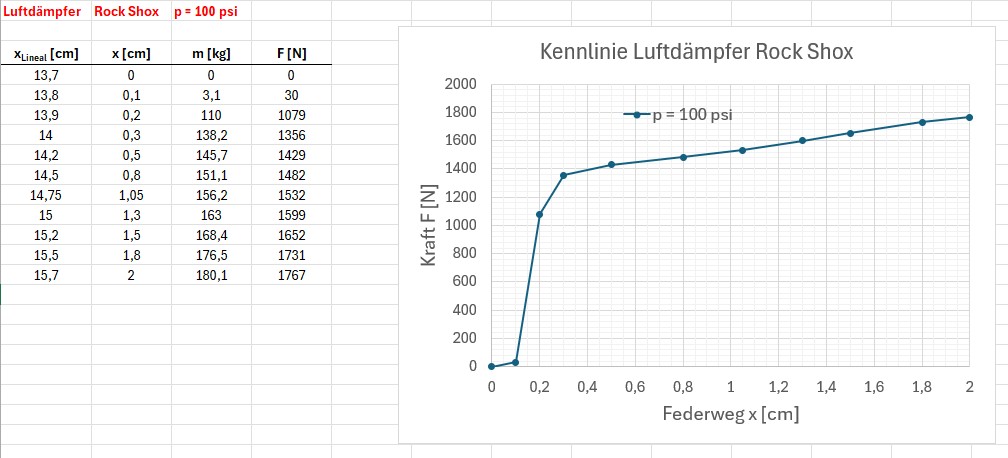
Beim Luftdämpfer von Rock Shox erhalte ich eine deutlich andere Kennlinie:
Innendruck p = 100 psi = ca. 7 bar:
Innendruck p = 50 psi = ca. 3.5 bar:
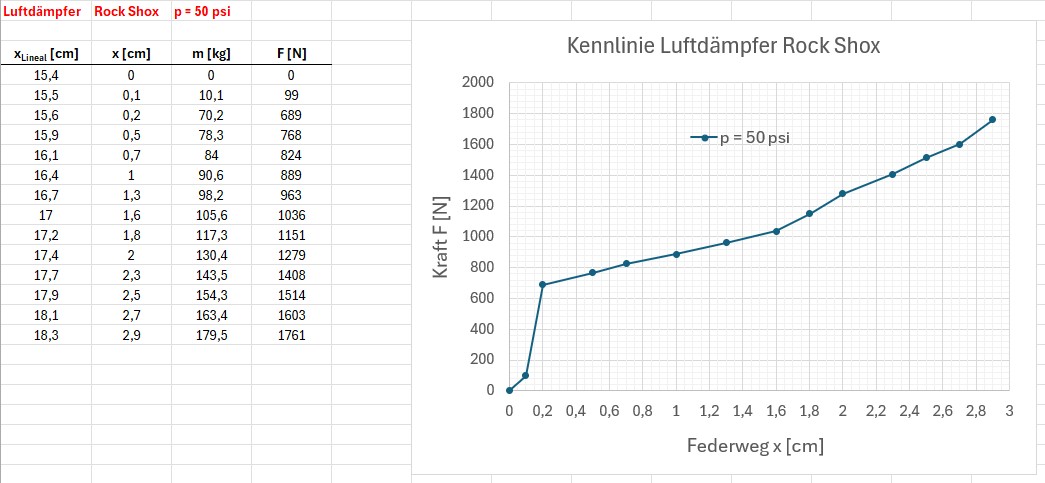
Die notwendige Kraft schnellt gleich zu Beginn innerhalb der ersten 2 mm auf einen sehr hohen Wert. Danach steigt die Kennlinie sehr wenig weiter an. Nur bei p = 50 psi erkennt man dann ansatzweise den Beginn eines progressiven Verlaufs, wie man sich ihn bei einem Luftdämpfer auch erwartet. Aber mich verwundert das extrem unsensible Ansprechverhalten des Luftdämpfers. Bei 100 psi sind gleich zu Beginn 1400 N und bei 50 psi immerhin 700 N notwendig. Sprechen Luftdämpfer wirklich dermaßen schlecht an?
Da der mit der Personenwaage erfassbare Kraftbereich von 1800 N für die Dämpfer nicht ausreicht, habe ich noch einmal ins Geldtascherl gegriffen und einen weiteren Sensor auf aliexpress geordert. Dieser sollte Kräfte bis 500 kg = ca. 5000 N erfassen können:
Der 500 kg Kraftsensor ist bereits nach rund 10 Tagen angekommen:





Ein HX711 in Kombination mit einem Arduino sorgen für den Betrieb des Sensors.
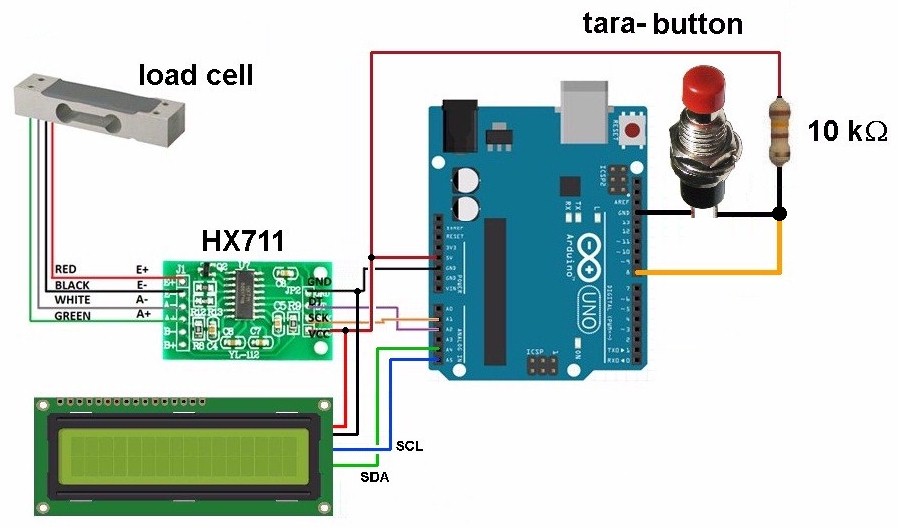


Der kurze Arduino-Code:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 |
#include <LiquidCrystal_I2C.h> #include <Wire.h> LiquidCrystal_I2C lcd(0x27,16,2); // set the LCD address to 0x27 for a 16 chars and 2 line display. ACHTUNG: Adresse kann auch 0x3F sein !!! // Anschlüsse: // GND - GND // VCC - 5V // SDA - ANALOG Pin 4 // SCL - ANALOG pin 5 #include <HX711.h> HX711 scale(A2, A1); long Rohwert; // vom HX711 gelieferter Rohwert long offset; // offset float Kraft; // berechnete Kraft in N const int buttonPin = 8; // the number of the pushbutton pin int buttonState = 0; // variable for reading the pushbutton status // ===================== // ======= SETUP ======= // ===================== void setup() { Serial.begin(9600); scale.set_gain(128); // A-Kanal: gain = 64 oder 128; B-Kanal: fix 32 pinMode(buttonPin, INPUT); lcd.begin(); // initialize the lcd // Print a message to the LCD. lcd.backlight(); lcd.setCursor(2,0); lcd.print("Kraftmesser"); delay(2000); lcd.setCursor(2,0); lcd.print(" "); lcd.setCursor(0,0); lcd.print("F = "); offset = scale.read_average(20); // Einlesen von 20 Rohwerten zur Ermittlung des tara (offset) } // ============================ // ======= HAUPTSCHLEIFE ====== // ============================ void loop() { buttonState = digitalRead(buttonPin); // button for new tara (offset) if (buttonState == LOW) { offset = scale.read_average(20); // Einlesen von 20 Rohwerten zur Ermittlung des tara (offset) } Rohwert = scale.read_average(10); // Einlesen von 10 Rohwerten Serial.print("Rohwert = "); Serial.print(Rohwert); Kraft = -0.00149 * (Rohwert - offset); // Berechnung der Kraft in Newton Serial.print(" Kraft = "); Serial.println(Kraft); lcd.setCursor(4,0); lcd.print(Kraft,1); lcd.print(" N "); delay(50); } |
Die Kalibrierung erfolgte mit der kompakten Personenwaage:







Damit war mein Aufbau bereit für quantitative Messungen.
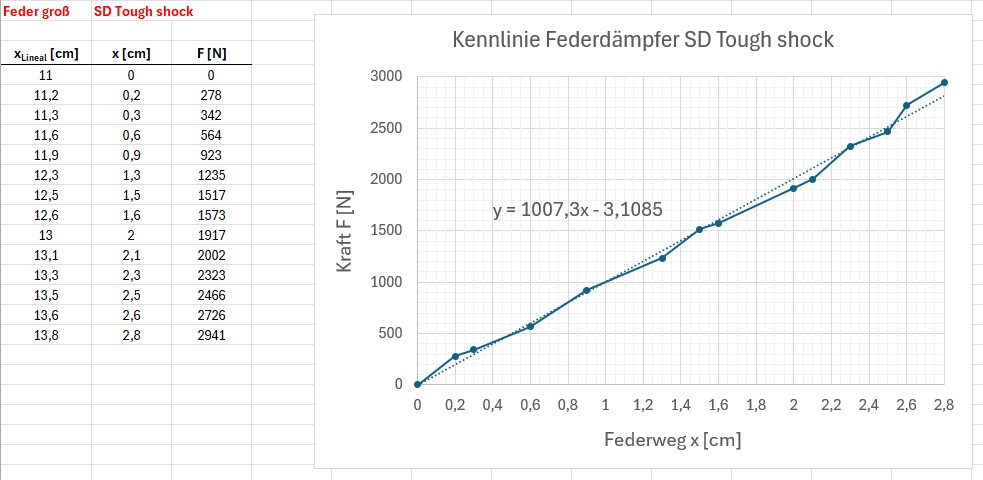
Federdämpfer 1:



Die Kennlinie glich wie zu erwarten war der Hook’schen Gerade:
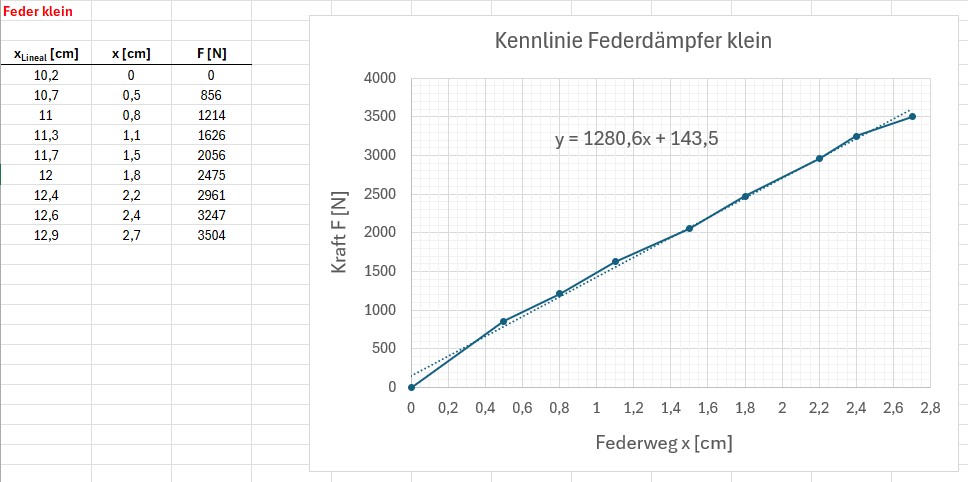
Federdämpfer 2:




Auch dieser Graph entsprach den Erwartungen. Die Federkonstante beträgt konkret 1281 N/cm. Die Feder ist wie schon erwähnt mit 750 lbs/inch = 1313 N/cm gekennzeichnet, also nahezu perfekte Übereinstimmung 😉
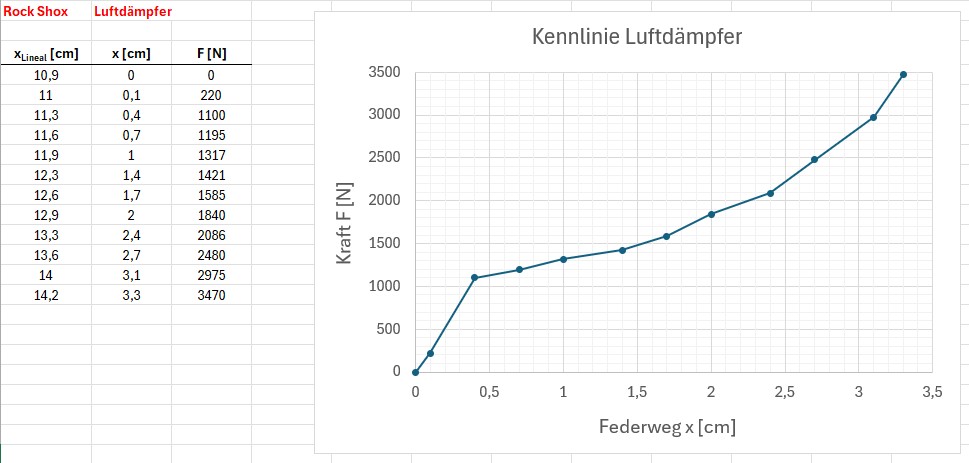
Luftdämpfer:




Mit meiner nur bis 180 kg reichenden Personenwaage konnte ich ja die Kennlinie des Luftdämpfers nicht ausreichend erfassen. Jetzt mit dem 500 kg Kraftsensor ging es schon deutlich besser. Man erkennt nun gut den progressiven Verlauf bei zunehmenden Federweg:
Damit ist auch dieses Projekt für mich abgeschlossen. Gekostet hat mich der gesamte Aufbau inkl. Dämpfern so um die 120 Euro, also noch überschaubar.

